1.5.1正弦函数的图象与性质再认识 课件(共47张PPT)——2020-2021学年高一下学期北师大版(2019)必修第二册第一章第五节
文档属性
| 名称 | 1.5.1正弦函数的图象与性质再认识 课件(共47张PPT)——2020-2021学年高一下学期北师大版(2019)必修第二册第一章第五节 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 00:00:00 | ||
图片预览









文档简介
正弦函数的图象与性质再认识
授课教师:
温故知新
学习目标
1. 理解正弦函数图象的画法. (重点)
2. 认识图象理解正弦函数的性质. (重点、难点)
3.通过三角函数的三种画法,体会用“五点
法”作图的好处,并学会熟练地画出一些
较简单的正弦函数的图象.(重点)
课文精讲
在1.3中引入了弧度制,在1.4中我们借助单位圆学习了正弦函数、余弦函数的概念、性
质和诱导公式.从现在起,正弦函数和余弦函数分别表示为y=sinx和y=cosx,并在平面直角作标系中讨论它们的图象和性质.
导入
课文精讲
应该注意到,由于自变量x是用弧度表示的,这里讨论的函数y=sinx和y=cosx都是R的两个子集中元素之间的对应,它们都是周期函数,自变量x可以与角度无关.因此,自然界大量的周期现象(如简谐振动、潮汐现象等)都可以用
这类函数来描述.
导入
课文精讲
正弦函数的图象
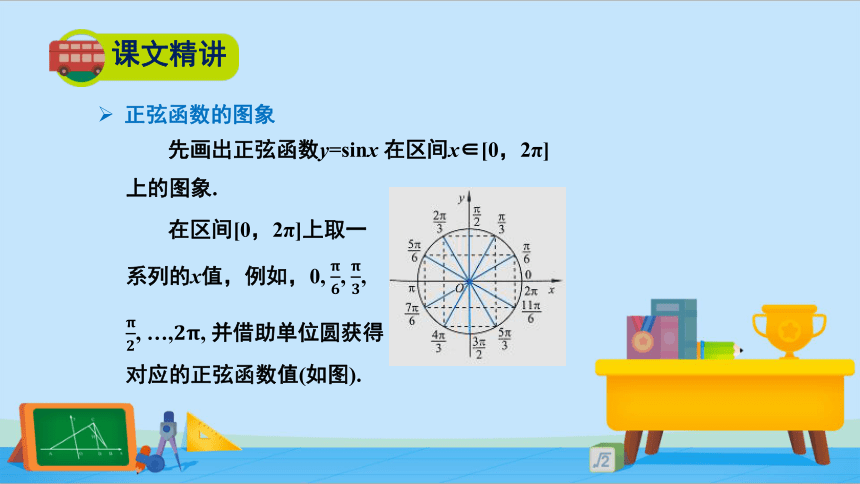
先画出正弦函数y=sinx 在区间x∈[0,2π]上的图象.
在区间[0,2π]上取一系列的x值,例如,0, ????????, ????????, ????????, …,????????, 并借助单位圆获得对应的正弦函数值(如图).
?
课文精讲
正弦函数的图象
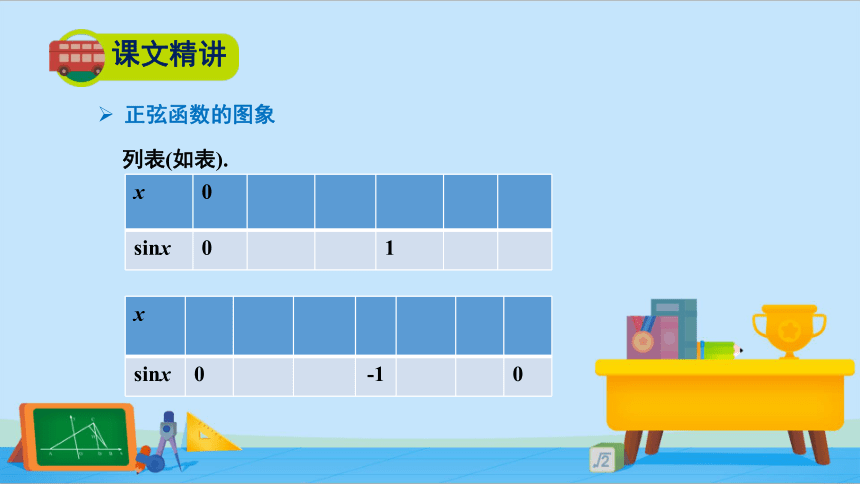
列表(如表).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
????????
????????
????????
????????????
????????????
sinx
0
????????
????????
1
????????
????????
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
????
????????????
????????????
????????????
????????????
????????????????
????????
sinx
0
?????????
?????????
-1
?????????
?????????
0
课文精讲
正弦函数的图象
利用表中的数据,先在平面直角坐标系内描点,结合对函数y=sinx性质的了解,用光滑曲线顺次连接,就可以得到函数y=sinx在区间[0,2π]上的图象(如图).
课文精讲
正弦函数的图象
思考
根据函数y=sinx,x∈[0, 2π]的图象,你能想象函数y=sinx,x∈R的图象吗?
课文精讲
正弦函数的图象
将函数y=sinx,x∈[0, 2π]的图象向左、右平移(每次平移2π个单位长度),就可以得
到正弦函数y=sinx,x ∈ R的图象(如图).正弦函数的图象称作正弦曲线.
这就是正弦函数图象的几何画法
课文精讲
正弦函数性质的再认识
请观察正弦函数的图象(如图),进一步理解正弦函数的性质.
课文精讲
正弦函数性质的再认识
1.定义域
正弦函数的定义域是R.
课文精讲
正弦函数性质的再认识
2.周期性
从正弦函数的图象(如图)可以看到,当自变量x的值增加2π的整数倍时,函数值重复出现.即正弦函数是周期函数,它的最小正周期为2π.同样,也可以从诱导公式sin(x+2kπ)=sin x,k∈Z中得到正弦函数的最小正周期为2π.
课文精讲
正弦函数性质的再认识
2.周期性
因此,为了研究问题方便,可以任意选取一个2π长度的区间,讨论y=sinx的性质,然
后延拓到定义域R上.
课文精讲
正弦函数性质的再认识
3.单调性
在正弦函数y=sinx图象中,选取长度为2π的区间[ , ],观察图,可以看出:
当x由-????????增大到????????时,sinx的值由-1增大到1;当x由????????增大到????????????时,sinx的值由1减小到-1.
?
?????????
?
????????????
?
课文精讲
正弦函数性质的再认识
3.单调性
因此,正弦函数在区间[?????????, ????????]上单调递增,在区间[????????,????????????]上单调递减.
?
课文精讲
正弦函数性质的再认识
3.单调性
由正弦函数的周期性可知,正弦函数在每一个区间[2kπ-????????,2kπ+ ????????] ,k∈Z上都单调递增,在每一个区间[2kπ+????????,2kπ+????????????] , k∈Z上都单调递减.
?
课文精讲
正弦函数性质的再认识
4.最大(小)值和值域
设集合A=????=????????????+??????????,????∈???? ,
B=????=????????????+??????????????,????∈???? ,
当x∈A时,正弦函数y=sinx取得最大值1;反之,当正弦函数y=sinx达到最大值1时, x∈A.
?
课文精讲
正弦函数性质的再认识
4.最大(小)值和值域
设集合A=????=????????????+??????????,????∈???? ,
B=????=????????????+??????????????,????∈???? ,
当x∈B时,正弦函数y=sinx取得最小值-1;反之,当正弦函数y=sinx达到最小值-1时, x∈B.
?
课文精讲
正弦函数性质的再认识
4.最大(小)值和值域
从正弦函数的图象(如图)可以看出,正弦曲线夹在两条平行线y=1和y=-1之间,所以正弦函数的值域是[-1,1].
课文精讲
正弦函数性质的再认识
5.奇偶性
正弦曲线关于原点对称,如图.由诱导公式sin(-x)=-sinx可知,正弦函数是奇函数.
课文精讲
正弦函数性质的再认识
思考交流
探索正弦函数图象的对称性.它有对称轴吗?有对称中心吗?
有,对称轴是kπ+????????,对称中心是kπ.
?
典型例题
例1:比较下列各组三角函数值的大小:
(1) 与 ;
(2) 与 .
解: (1)如图.
sin?????????????
?
sin?????????????
?
sin?????????????????
?
sin?????????????????
?
因为-??????????
典型例题
例1:比较下列各组三角函数值的大小:
(1) 与 ;
(2) 与 .
解: (2)如图.
sin?????????????
?
sin?????????????
?
sin?????????????????
?
sin?????????????????
?
sin ??????????????????= sin ????????+?????????????= sin?????????????,
sin?????????????????= sin ????????+?????????????= sin?????????????.
?
典型例题
例1:比较下列各组三角函数值的大小:
(1) 与 ;
(2) 与 .
解: (2)如图.
sin?????????????
?
sin?????????????
?
sin?????????????????
?
sin?????????????????
?
因为??????????
课文精讲
五点(画图)法
思考
在确定正弦函数的图象形状时,应抓住哪些关键点?
课文精讲
五点(画图)法
在一个周期内,例如[[0,2π],从正弦函数的图象(如图)可以看出:x=0,π, 2π是
y=sinx的零点; , 分别是y=sinx的最大值点、最小值点.它们在正弦曲线中起着关键作用.
x=?????????
?
?????????????
?
课文精讲
五点(画图)法
根据正弦曲线的基本性质,描出 (0,0) ( ,1), (π,0) ,( ,-1), (2π,0)这五个关键点后,函数y=sinx,x∈[0,2π]的图象就基本确定了(如图).
?????????
?
?????????????
?
课文精讲
五点(画图)法
因此,在精确度要求不太高时,常常先描出这五个关键点,然后用光滑曲线将它们顺次连接起来,就得到正弦函数的简图.这种作正弦曲线的方法称为“五点(画图)法”.
课文精讲
五点(画图)法
用“五点法”作正弦曲线的一般步骤:
(1)先描出(0,0),(????????,1),(π,0),(??????????,
-1),(2π,0)这五个点;
(2)把这五个点用一条光滑的曲线连接起来,就得
到了y=sinx在[0,2π]上的简图;
(3)通过左、右平移(每次平移2π个单位长度)即
可得到正弦函数y=sinx(x∈R)的图象.
?
课文精讲
五点(画图)法
三种作图方法的比较
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}作图方法
主要步骤
优劣
描点法
列表 描点
连线
只能取近似值,误差较大
几何法
利用单位圆,使x0在[0,2π]上取足够多的值,画出足够多的点T(x0,sinx0)
较精确,但步骤繁琐
课文精讲
五点(画图)法
三种作图方法的比较
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}作图方法
主要步骤
优劣
五点法
描最高点、最低点、图象与x轴的三个交点
实用、高效
典型例题
例1:画出函数y=sinx在区间[0,2π]上的图象.
解:利用五个关键点确定y=sinx的图象.这五
个关键点也是画y=?sinx图象的关键点.按
五个关键点列表(如表).
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
????????
π
????????????
2π
y=sinx
0
1
0
-1
0
y=-sinx
0
-1
0
1
0
典型例题
例1:画出函数y=sinx在区间[0,2π]上的图象.
解:于是得到函数y=?sinx在区间[0,2π]的五
个关键点为(0,0) ,( ,-1),(π,0),
( ,1),(2π,0).
?
?????????
?
?????????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
????????
π
????????????
2π
y=sinx
0
1
0
-1
0
y=-sinx
0
-1
0
1
0
典型例题
例1:画出函数y=sinx在区间[0,2π]上的图象.
解: 描点,并用光滑曲线将它们顺次连接起
来,就画出函数y=?sinx在区间[0,2π]上
的图象,如图.
?
典型例题
例2:画出函数y=sinx-1的图象,并讨论它的性质.
解:函数y=sinx的周期是2π,按五个关键点
列表(如表).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
????????
π
????????????
2π
y=sinx
0
1
0
-1
0
y=sinx-1
-1
0
-1
-2
-1
典型例题
例2:画出函数y=sinx-1的图象,并讨论它的性质.
解:于是得到函数y=sinx-1在[0,2π]上的五
个关键点为(0,-1) ,( ,0),(π,-1),
( ,-2),(2π,-1).
?????????
?
?????????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
????????
π
????????????
2π
y=sinx
0
1
0
-1
0
y=sinx-1
-1
0
-1
-2
-1
典型例题
例2:画出函数y=sinx-1的图象,并讨论它的性质.
解:描点,并用光滑曲线将它们顺次连接起
来,就画出函数y=sinx-1在区间[0,2π]
上的图象.将其按周期延拓到R上得到
y=sinx-1在实数集上的图象,如图.
典型例题
例2:画出函数y=sinx-1的图象,并讨论它的性质.
解:观察图象得出y=sinx-1的性质(如表).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}函数
y=sinx-1
定义域
R
值域
[-2,0]
奇偶性
既不是奇函数,也不是偶函数
周期性
周期函数,周期是2π
典型例题
例2:画出函数y=sinx-1的图象,并讨论它的性质.
解:观察图象得出y=sinx-1的性质(如表).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}函数
y=sinx-1
单调性
在每一个闭区间[2kπ- ,2kπ+ ]
都单调递增;
在每一个闭区间[2kπ+ ,2kπ+ ]
都单调递减
?????????
?
????????
?
?????????????
?
?????????
?
典型例题
例2:画出函数y=sinx-1的图象,并讨论它的性质.
解:观察图象得出y=sinx-1的性质(如表).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}函数
y=sinx-1
最大值与最小值
当x=2kπ+ ,k∈Z时,最大值为0;
当x=2kπ+ ,k∈Z时,最小值为-2
????????
?
?????????????
?
综合练习
函数y=2sinx-1的最小值是______.
解:由y=sinα的性质可得,其最小值为-1.
那么,函数y=2sinα-1的最小值:
y min=-2-1=-3.
故答案为:-3.
-3
综合练习
下列说法错误的有( )
A.作正弦函数的图象时,单位圆的半径长
与y轴的单位长度要一致
B.y=sinx,x∈[0,2π]的图象关于点P(π,0)
对称
C.y=sinx,x∈[ , ]的图象关于直线x=π
成轴对称
D.正弦函数y=sinx的图象不超出直线y=-1和
y=1所夹的区域
????????
?
????????????
?
综合练习
解:对于A,作正弦函数的图象时,单位圆的半径长与y轴的单位长度要一致,故A正确;
对于B,y=sinx,x∈[0,2π]的图象关于点P(π,0)对称,故B正确;
对于C, y=sinx,x ∈[ , ]的图象关于直线 成轴对称图形,故C错误;
对于D,正弦函数y=sinx的最大值为1,最小值为-1,故它的图象不超出直线y=-1和y=1所夹的区域,故D正确,
故选:C.
????????
?
????????????
?
x=????????????
?
综合练习
下列说法错误的有( )
A.作正弦函数的图象时,单位圆的半径长
与y轴的单位长度要一致
B.y=sinx,x∈[0,2π]的图象关于点P(π,0)
对称
C.y=sinx,x∈[ , ]的图象关于直线x=π
成轴对称
D.正弦函数y=sinx的图象不超出直线y=-1和
y=1所夹的区域
????????
?
????????????
?
C
本课小结
再 见
授课教师:
温故知新
学习目标
1. 理解正弦函数图象的画法. (重点)
2. 认识图象理解正弦函数的性质. (重点、难点)
3.通过三角函数的三种画法,体会用“五点
法”作图的好处,并学会熟练地画出一些
较简单的正弦函数的图象.(重点)
课文精讲
在1.3中引入了弧度制,在1.4中我们借助单位圆学习了正弦函数、余弦函数的概念、性
质和诱导公式.从现在起,正弦函数和余弦函数分别表示为y=sinx和y=cosx,并在平面直角作标系中讨论它们的图象和性质.
导入
课文精讲
应该注意到,由于自变量x是用弧度表示的,这里讨论的函数y=sinx和y=cosx都是R的两个子集中元素之间的对应,它们都是周期函数,自变量x可以与角度无关.因此,自然界大量的周期现象(如简谐振动、潮汐现象等)都可以用
这类函数来描述.
导入
课文精讲
正弦函数的图象
先画出正弦函数y=sinx 在区间x∈[0,2π]上的图象.
在区间[0,2π]上取一系列的x值,例如,0, ????????, ????????, ????????, …,????????, 并借助单位圆获得对应的正弦函数值(如图).
?
课文精讲
正弦函数的图象
列表(如表).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
????????
????????
????????
????????????
????????????
sinx
0
????????
????????
1
????????
????????
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
????
????????????
????????????
????????????
????????????
????????????????
????????
sinx
0
?????????
?????????
-1
?????????
?????????
0
课文精讲
正弦函数的图象
利用表中的数据,先在平面直角坐标系内描点,结合对函数y=sinx性质的了解,用光滑曲线顺次连接,就可以得到函数y=sinx在区间[0,2π]上的图象(如图).
课文精讲
正弦函数的图象
思考
根据函数y=sinx,x∈[0, 2π]的图象,你能想象函数y=sinx,x∈R的图象吗?
课文精讲
正弦函数的图象
将函数y=sinx,x∈[0, 2π]的图象向左、右平移(每次平移2π个单位长度),就可以得
到正弦函数y=sinx,x ∈ R的图象(如图).正弦函数的图象称作正弦曲线.
这就是正弦函数图象的几何画法
课文精讲
正弦函数性质的再认识
请观察正弦函数的图象(如图),进一步理解正弦函数的性质.
课文精讲
正弦函数性质的再认识
1.定义域
正弦函数的定义域是R.
课文精讲
正弦函数性质的再认识
2.周期性
从正弦函数的图象(如图)可以看到,当自变量x的值增加2π的整数倍时,函数值重复出现.即正弦函数是周期函数,它的最小正周期为2π.同样,也可以从诱导公式sin(x+2kπ)=sin x,k∈Z中得到正弦函数的最小正周期为2π.
课文精讲
正弦函数性质的再认识
2.周期性
因此,为了研究问题方便,可以任意选取一个2π长度的区间,讨论y=sinx的性质,然
后延拓到定义域R上.
课文精讲
正弦函数性质的再认识
3.单调性
在正弦函数y=sinx图象中,选取长度为2π的区间[ , ],观察图,可以看出:
当x由-????????增大到????????时,sinx的值由-1增大到1;当x由????????增大到????????????时,sinx的值由1减小到-1.
?
?????????
?
????????????
?
课文精讲
正弦函数性质的再认识
3.单调性
因此,正弦函数在区间[?????????, ????????]上单调递增,在区间[????????,????????????]上单调递减.
?
课文精讲
正弦函数性质的再认识
3.单调性
由正弦函数的周期性可知,正弦函数在每一个区间[2kπ-????????,2kπ+ ????????] ,k∈Z上都单调递增,在每一个区间[2kπ+????????,2kπ+????????????] , k∈Z上都单调递减.
?
课文精讲
正弦函数性质的再认识
4.最大(小)值和值域
设集合A=????=????????????+??????????,????∈???? ,
B=????=????????????+??????????????,????∈???? ,
当x∈A时,正弦函数y=sinx取得最大值1;反之,当正弦函数y=sinx达到最大值1时, x∈A.
?
课文精讲
正弦函数性质的再认识
4.最大(小)值和值域
设集合A=????=????????????+??????????,????∈???? ,
B=????=????????????+??????????????,????∈???? ,
当x∈B时,正弦函数y=sinx取得最小值-1;反之,当正弦函数y=sinx达到最小值-1时, x∈B.
?
课文精讲
正弦函数性质的再认识
4.最大(小)值和值域
从正弦函数的图象(如图)可以看出,正弦曲线夹在两条平行线y=1和y=-1之间,所以正弦函数的值域是[-1,1].
课文精讲
正弦函数性质的再认识
5.奇偶性
正弦曲线关于原点对称,如图.由诱导公式sin(-x)=-sinx可知,正弦函数是奇函数.
课文精讲
正弦函数性质的再认识
思考交流
探索正弦函数图象的对称性.它有对称轴吗?有对称中心吗?
有,对称轴是kπ+????????,对称中心是kπ.
?
典型例题
例1:比较下列各组三角函数值的大小:
(1) 与 ;
(2) 与 .
解: (1)如图.
sin?????????????
?
sin?????????????
?
sin?????????????????
?
sin?????????????????
?
因为-??????????
典型例题
例1:比较下列各组三角函数值的大小:
(1) 与 ;
(2) 与 .
解: (2)如图.
sin?????????????
?
sin?????????????
?
sin?????????????????
?
sin?????????????????
?
sin ??????????????????= sin ????????+?????????????= sin?????????????,
sin?????????????????= sin ????????+?????????????= sin?????????????.
?
典型例题
例1:比较下列各组三角函数值的大小:
(1) 与 ;
(2) 与 .
解: (2)如图.
sin?????????????
?
sin?????????????
?
sin?????????????????
?
sin?????????????????
?
因为??????????
课文精讲
五点(画图)法
思考
在确定正弦函数的图象形状时,应抓住哪些关键点?
课文精讲
五点(画图)法
在一个周期内,例如[[0,2π],从正弦函数的图象(如图)可以看出:x=0,π, 2π是
y=sinx的零点; , 分别是y=sinx的最大值点、最小值点.它们在正弦曲线中起着关键作用.
x=?????????
?
?????????????
?
课文精讲
五点(画图)法
根据正弦曲线的基本性质,描出 (0,0) ( ,1), (π,0) ,( ,-1), (2π,0)这五个关键点后,函数y=sinx,x∈[0,2π]的图象就基本确定了(如图).
?????????
?
?????????????
?
课文精讲
五点(画图)法
因此,在精确度要求不太高时,常常先描出这五个关键点,然后用光滑曲线将它们顺次连接起来,就得到正弦函数的简图.这种作正弦曲线的方法称为“五点(画图)法”.
课文精讲
五点(画图)法
用“五点法”作正弦曲线的一般步骤:
(1)先描出(0,0),(????????,1),(π,0),(??????????,
-1),(2π,0)这五个点;
(2)把这五个点用一条光滑的曲线连接起来,就得
到了y=sinx在[0,2π]上的简图;
(3)通过左、右平移(每次平移2π个单位长度)即
可得到正弦函数y=sinx(x∈R)的图象.
?
课文精讲
五点(画图)法
三种作图方法的比较
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}作图方法
主要步骤
优劣
描点法
列表 描点
连线
只能取近似值,误差较大
几何法
利用单位圆,使x0在[0,2π]上取足够多的值,画出足够多的点T(x0,sinx0)
较精确,但步骤繁琐
课文精讲
五点(画图)法
三种作图方法的比较
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}作图方法
主要步骤
优劣
五点法
描最高点、最低点、图象与x轴的三个交点
实用、高效
典型例题
例1:画出函数y=sinx在区间[0,2π]上的图象.
解:利用五个关键点确定y=sinx的图象.这五
个关键点也是画y=?sinx图象的关键点.按
五个关键点列表(如表).
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
????????
π
????????????
2π
y=sinx
0
1
0
-1
0
y=-sinx
0
-1
0
1
0
典型例题
例1:画出函数y=sinx在区间[0,2π]上的图象.
解:于是得到函数y=?sinx在区间[0,2π]的五
个关键点为(0,0) ,( ,-1),(π,0),
( ,1),(2π,0).
?
?????????
?
?????????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
????????
π
????????????
2π
y=sinx
0
1
0
-1
0
y=-sinx
0
-1
0
1
0
典型例题
例1:画出函数y=sinx在区间[0,2π]上的图象.
解: 描点,并用光滑曲线将它们顺次连接起
来,就画出函数y=?sinx在区间[0,2π]上
的图象,如图.
?
典型例题
例2:画出函数y=sinx-1的图象,并讨论它的性质.
解:函数y=sinx的周期是2π,按五个关键点
列表(如表).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
????????
π
????????????
2π
y=sinx
0
1
0
-1
0
y=sinx-1
-1
0
-1
-2
-1
典型例题
例2:画出函数y=sinx-1的图象,并讨论它的性质.
解:于是得到函数y=sinx-1在[0,2π]上的五
个关键点为(0,-1) ,( ,0),(π,-1),
( ,-2),(2π,-1).
?????????
?
?????????????
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
0
????????
π
????????????
2π
y=sinx
0
1
0
-1
0
y=sinx-1
-1
0
-1
-2
-1
典型例题
例2:画出函数y=sinx-1的图象,并讨论它的性质.
解:描点,并用光滑曲线将它们顺次连接起
来,就画出函数y=sinx-1在区间[0,2π]
上的图象.将其按周期延拓到R上得到
y=sinx-1在实数集上的图象,如图.
典型例题
例2:画出函数y=sinx-1的图象,并讨论它的性质.
解:观察图象得出y=sinx-1的性质(如表).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}函数
y=sinx-1
定义域
R
值域
[-2,0]
奇偶性
既不是奇函数,也不是偶函数
周期性
周期函数,周期是2π
典型例题
例2:画出函数y=sinx-1的图象,并讨论它的性质.
解:观察图象得出y=sinx-1的性质(如表).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}函数
y=sinx-1
单调性
在每一个闭区间[2kπ- ,2kπ+ ]
都单调递增;
在每一个闭区间[2kπ+ ,2kπ+ ]
都单调递减
?????????
?
????????
?
?????????????
?
?????????
?
典型例题
例2:画出函数y=sinx-1的图象,并讨论它的性质.
解:观察图象得出y=sinx-1的性质(如表).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}函数
y=sinx-1
最大值与最小值
当x=2kπ+ ,k∈Z时,最大值为0;
当x=2kπ+ ,k∈Z时,最小值为-2
????????
?
?????????????
?
综合练习
函数y=2sinx-1的最小值是______.
解:由y=sinα的性质可得,其最小值为-1.
那么,函数y=2sinα-1的最小值:
y min=-2-1=-3.
故答案为:-3.
-3
综合练习
下列说法错误的有( )
A.作正弦函数的图象时,单位圆的半径长
与y轴的单位长度要一致
B.y=sinx,x∈[0,2π]的图象关于点P(π,0)
对称
C.y=sinx,x∈[ , ]的图象关于直线x=π
成轴对称
D.正弦函数y=sinx的图象不超出直线y=-1和
y=1所夹的区域
????????
?
????????????
?
综合练习
解:对于A,作正弦函数的图象时,单位圆的半径长与y轴的单位长度要一致,故A正确;
对于B,y=sinx,x∈[0,2π]的图象关于点P(π,0)对称,故B正确;
对于C, y=sinx,x ∈[ , ]的图象关于直线 成轴对称图形,故C错误;
对于D,正弦函数y=sinx的最大值为1,最小值为-1,故它的图象不超出直线y=-1和y=1所夹的区域,故D正确,
故选:C.
????????
?
????????????
?
x=????????????
?
综合练习
下列说法错误的有( )
A.作正弦函数的图象时,单位圆的半径长
与y轴的单位长度要一致
B.y=sinx,x∈[0,2π]的图象关于点P(π,0)
对称
C.y=sinx,x∈[ , ]的图象关于直线x=π
成轴对称
D.正弦函数y=sinx的图象不超出直线y=-1和
y=1所夹的区域
????????
?
????????????
?
C
本课小结
再 见
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
