2020-2021学年高一下学期数学人教A版必修4第一章1.1.1任意角 课件(共24张PPT)
文档属性
| 名称 | 2020-2021学年高一下学期数学人教A版必修4第一章1.1.1任意角 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 206.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 00:00:00 | ||
图片预览








文档简介
《任意角》
·人教版必修四数学PPT课件·
目
录
1
学习目标
2
新课导入
3
新课讲授
4
课堂总结
学习
目标
(1)推广角的概念、引入大于角和负角;
(2)理解并掌握正角、负角、零角的定义;
(3)理解任意角以及象限角的概念;
(4)掌握所有与角终边相同的角(包括角)的表示方法;
(5)树立运动变化观点,深刻理解推广后的角的概念;
1-学习目标
新课
导入
2-新课导入
1-体操上有直体后空翻转体720度的高难度动作,直体前空翻转体360度接直体前空翻转体540度,俄式挺身转体1080度,直体后空翻转体900度以及团身后空翻两周转体360度
2-新课导入
2-花样游泳中,跳水运动员旋转的周数如何用角度计算来表示?
2-新课导入
旋转方向也有顺时针与逆时针
3-汽车在前进和倒车中,车轮转动的角度如何表示才比较合理?
2-新课导入
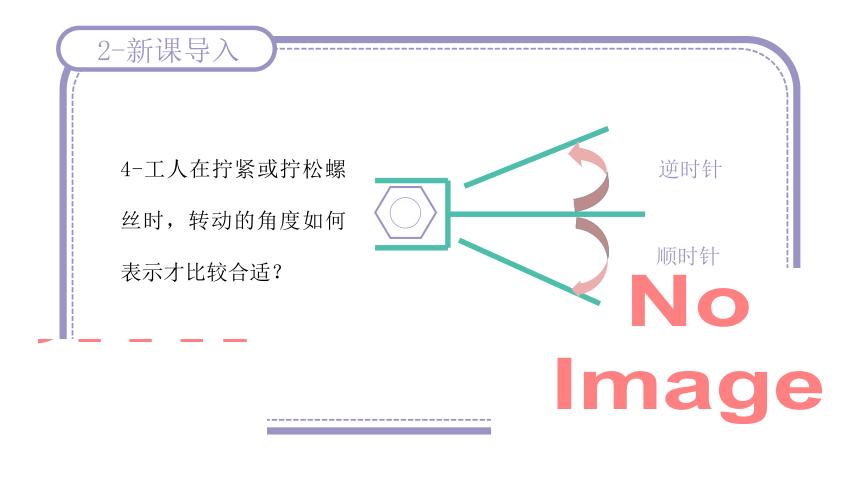
4-工人在拧紧或拧松螺丝时,转动的角度如何表示才比较合适?
逆时针
顺时针
新课
讲授
从一个点出发引出的两条射线构成的几何图形。
角是平面几何中的一个基本图形,角是可以度量大小的,在平面几何中,角的取值范围如何?
角的范围:0°~360°
锐角
直角
钝角
平角
周角
╭╮
●
●
●
●
●
3-新课讲授
初中角的定义
3-新课讲授
对于角的图形特点有如下两种认识:
图1
②角是由平面内一条射线绕其端点从一个位置旋转到另一个位置所组成的图形(图2).
①角是由平面内一点引出的两条射线所组成的图形(图1);
图2
思考 1:
3-新课讲授
一条射线绕着它的端点在平面内旋转形成的图形。在不引起混淆的情况下,角α或∠α,可简记成α;
“旋转”形成角
o
A
B
始边
终边
顶点
任意角
注1
角的概念是通过角的终边的运动来推广的,角的四个“要素”是:顶点、始边、终边和旋转方向.
3-新课讲授
60°
-60°
一般地,一条射线绕其端点旋转,既可以按逆时针方向旋转,也可以按顺时针方向旋转.
你认为将一条射线绕其端点按逆时针方向旋转600所形成的角,与按顺时针方向旋转600所形成的角是否相等?
思考 2:
为了区分形成角的两种不同的旋转方向,可作怎样的规定?如果一条射线没有作任何旋转,它还形成一个角吗?
思考 3:
3-新课讲授
正角:按逆时针方向旋转形成的角
负角:按顺时针方向旋转形成的角
零角:一条射线没有作任何旋转形成的角(零角的始边与终边重合)
任意角
任意角的定义
注2
①角度的范围不再限于00~3600 ;
②确定任意角的度数要抓住旋转方向及旋转圈数;
③当角的始边相同时,角相等则终边相同,但终边相同的角不一定相等.
④引入正、负角的概念后,角的加减运算类似于实数的加减运算.
3-新课讲授
β
B2
γ
A
B1
α
O
“四要素”是:
顶点、始边、终边和旋转方向.
作出角
练习 1:
提示
先画一条射线作为角的始边(在直角坐标系中,以x轴正半轴为始边),再由角的正负确定角的旋转方向,再由角的绝对值大小确定角的旋转量,最后画出角的终边,并用带箭头的螺旋线加以标注.
3-新课讲授
任意两个角的数量大小可以相加、相减.例如50°+80°=130°, 50°-80°=-30°,
你能解释一下这两个式子的几何意义吗?
130°是以50°角的终边为始边,逆时针旋转80°所成的角.
-30°是以50°角的终边为始边,顺时针旋转80°所成的角.
练习 2:
负角
如果你的手表慢了20分钟,或快了1.25小时,应该将分针分别旋转多少度才能将时间校准?
-120°,450°
问:钟表的指针旋转所成的角总是_______.
练习 2:
3-新课讲授
为进一步研究角的需要,常在直角坐标系内讨论角:我们使角α的顶点与原点重合,始边与x轴的正半轴重合,
角α的终边落在第几象限,则称角α 为第几象限角;
角α的终边落在坐标轴上,则称角α 为轴线角;
x
o
y
2-象限角和轴线角
3-新课讲授
-50°,405°,210°, -200°, - 450°分别是第几象限的角?
-50°
x
y
o
x
y
o
210°
x
y
o
405°
x
y
o
-200°
-450°
x
y
o
练习 1:
3-新课讲授
③第二象限的角一定比第一象限的角大吗?
☆象限角只能反映角的终边所在象限,
不能反映角的大小.
①准确区分“锐角”和“第一象限角”,“钝角”和“第二象限角”。锐角是第一象限角,钝角是第二象限角;反之不然.
练习 2:
②准确区分:
锐角:0°<α<90°;0°~90°的角:0°≤α<90°;小于90°的角:α<90°(包括负角)
问:集合M={小于90°的角}, N={锐角}的关系如何?
3-新课讲授
一般地,所有与角α终边相同的角,连同角α在内所构成的集合S可以表示为:
即任一与α终边相同的角,都可以表示成角α与整数个周角的和.
3-终边相同的角
注3
(1)α为任意角;
(2)k∈Z这一条件必不可少;
(3)终边相同的角不一定相等,终边相等的角有无数多个,它们相差360°的整数倍。
问
终边与始边重合的角是零角吗?表示出符合条件的所有角构成的集合.
终边和始边重合的角不一定是零角,又如360°, -720°等.
课堂
总结
4-课堂总结
1-任意角的概念
(1)按逆时针方向旋转形成的角叫做正角;
(2)按顺时针方向旋转形成的角叫做负角;
(3)若射线没有任何旋转,则形成零角。
2-象限角
(1)角的终边在第几象限,就说这个角是第几象限角;
(2)角的终边在坐标轴上,就说这个角不属于任何象限;
3-终边相同的角
注:终边相同的角不一定相等,终边相等的角有无数多个,它们相差360°的整数倍。
同学们,下课啦!
·人教版必修四数学PPT课件·
·人教版必修四数学PPT课件·
目
录
1
学习目标
2
新课导入
3
新课讲授
4
课堂总结
学习
目标
(1)推广角的概念、引入大于角和负角;
(2)理解并掌握正角、负角、零角的定义;
(3)理解任意角以及象限角的概念;
(4)掌握所有与角终边相同的角(包括角)的表示方法;
(5)树立运动变化观点,深刻理解推广后的角的概念;
1-学习目标
新课
导入
2-新课导入
1-体操上有直体后空翻转体720度的高难度动作,直体前空翻转体360度接直体前空翻转体540度,俄式挺身转体1080度,直体后空翻转体900度以及团身后空翻两周转体360度
2-新课导入
2-花样游泳中,跳水运动员旋转的周数如何用角度计算来表示?
2-新课导入
旋转方向也有顺时针与逆时针
3-汽车在前进和倒车中,车轮转动的角度如何表示才比较合理?
2-新课导入
4-工人在拧紧或拧松螺丝时,转动的角度如何表示才比较合适?
逆时针
顺时针
新课
讲授
从一个点出发引出的两条射线构成的几何图形。
角是平面几何中的一个基本图形,角是可以度量大小的,在平面几何中,角的取值范围如何?
角的范围:0°~360°
锐角
直角
钝角
平角
周角
╭╮
●
●
●
●
●
3-新课讲授
初中角的定义
3-新课讲授
对于角的图形特点有如下两种认识:
图1
②角是由平面内一条射线绕其端点从一个位置旋转到另一个位置所组成的图形(图2).
①角是由平面内一点引出的两条射线所组成的图形(图1);
图2
思考 1:
3-新课讲授
一条射线绕着它的端点在平面内旋转形成的图形。在不引起混淆的情况下,角α或∠α,可简记成α;
“旋转”形成角
o
A
B
始边
终边
顶点
任意角
注1
角的概念是通过角的终边的运动来推广的,角的四个“要素”是:顶点、始边、终边和旋转方向.
3-新课讲授
60°
-60°
一般地,一条射线绕其端点旋转,既可以按逆时针方向旋转,也可以按顺时针方向旋转.
你认为将一条射线绕其端点按逆时针方向旋转600所形成的角,与按顺时针方向旋转600所形成的角是否相等?
思考 2:
为了区分形成角的两种不同的旋转方向,可作怎样的规定?如果一条射线没有作任何旋转,它还形成一个角吗?
思考 3:
3-新课讲授
正角:按逆时针方向旋转形成的角
负角:按顺时针方向旋转形成的角
零角:一条射线没有作任何旋转形成的角(零角的始边与终边重合)
任意角
任意角的定义
注2
①角度的范围不再限于00~3600 ;
②确定任意角的度数要抓住旋转方向及旋转圈数;
③当角的始边相同时,角相等则终边相同,但终边相同的角不一定相等.
④引入正、负角的概念后,角的加减运算类似于实数的加减运算.
3-新课讲授
β
B2
γ
A
B1
α
O
“四要素”是:
顶点、始边、终边和旋转方向.
作出角
练习 1:
提示
先画一条射线作为角的始边(在直角坐标系中,以x轴正半轴为始边),再由角的正负确定角的旋转方向,再由角的绝对值大小确定角的旋转量,最后画出角的终边,并用带箭头的螺旋线加以标注.
3-新课讲授
任意两个角的数量大小可以相加、相减.例如50°+80°=130°, 50°-80°=-30°,
你能解释一下这两个式子的几何意义吗?
130°是以50°角的终边为始边,逆时针旋转80°所成的角.
-30°是以50°角的终边为始边,顺时针旋转80°所成的角.
练习 2:
负角
如果你的手表慢了20分钟,或快了1.25小时,应该将分针分别旋转多少度才能将时间校准?
-120°,450°
问:钟表的指针旋转所成的角总是_______.
练习 2:
3-新课讲授
为进一步研究角的需要,常在直角坐标系内讨论角:我们使角α的顶点与原点重合,始边与x轴的正半轴重合,
角α的终边落在第几象限,则称角α 为第几象限角;
角α的终边落在坐标轴上,则称角α 为轴线角;
x
o
y
2-象限角和轴线角
3-新课讲授
-50°,405°,210°, -200°, - 450°分别是第几象限的角?
-50°
x
y
o
x
y
o
210°
x
y
o
405°
x
y
o
-200°
-450°
x
y
o
练习 1:
3-新课讲授
③第二象限的角一定比第一象限的角大吗?
☆象限角只能反映角的终边所在象限,
不能反映角的大小.
①准确区分“锐角”和“第一象限角”,“钝角”和“第二象限角”。锐角是第一象限角,钝角是第二象限角;反之不然.
练习 2:
②准确区分:
锐角:0°<α<90°;0°~90°的角:0°≤α<90°;小于90°的角:α<90°(包括负角)
问:集合M={小于90°的角}, N={锐角}的关系如何?
3-新课讲授
一般地,所有与角α终边相同的角,连同角α在内所构成的集合S可以表示为:
即任一与α终边相同的角,都可以表示成角α与整数个周角的和.
3-终边相同的角
注3
(1)α为任意角;
(2)k∈Z这一条件必不可少;
(3)终边相同的角不一定相等,终边相等的角有无数多个,它们相差360°的整数倍。
问
终边与始边重合的角是零角吗?表示出符合条件的所有角构成的集合.
终边和始边重合的角不一定是零角,又如360°, -720°等.
课堂
总结
4-课堂总结
1-任意角的概念
(1)按逆时针方向旋转形成的角叫做正角;
(2)按顺时针方向旋转形成的角叫做负角;
(3)若射线没有任何旋转,则形成零角。
2-象限角
(1)角的终边在第几象限,就说这个角是第几象限角;
(2)角的终边在坐标轴上,就说这个角不属于任何象限;
3-终边相同的角
注:终边相同的角不一定相等,终边相等的角有无数多个,它们相差360°的整数倍。
同学们,下课啦!
·人教版必修四数学PPT课件·
