1.7正切函数-【新教材】2020-2021学年北师大版(2019)高中数学必修第二册课件(46张PPT)
文档属性
| 名称 | 1.7正切函数-【新教材】2020-2021学年北师大版(2019)高中数学必修第二册课件(46张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 00:00:00 | ||
图片预览










文档简介
正切函数
授课教师:
温故知新
学习目标
1. 理解正切函数的定义. (重点)
2.掌握正切函数的诱导公式,并能够灵活运用其进行化简求值. (重点)
3. 会画y=tanx的图象.(重点)
4.推导并理解正切函数在区间?????????,????????内的性质.(难点)
5.能够利用正切函数的性质解决有关问题. (难点)
?
课文精讲
正切函数的定义
根据函数的定义,比值????????????????????????????????是x的函数,称为x的正切函数,记作y=tanx,其中定义域为{x∈R|x≠?????????+kπ,k∈Z}.
当x∈ ?????,?????????时,上述定义与初中时所学正切函数的定义是一致的.
?
典型例题
例1:求下列角α的正切函数值:
(1) α=- ?????????; (2) α= ?????????????.
?
解: (1) 因为α=- ?????????,所以sin??????????=?????????? ,
cos??????????=?????????,由正切函数的定义,得
?
tan??????????=-????????????????????????????????????????????=??????????????????? =?1;
?
典型例题
例1:求下列角α的正切函数值:
(1) α=- ?????????; (2) α= ?????????????.
?
解: (2) 因为α=?????????????,所以sin ?????????????=????????? ,
cos?????????????=?????????? ,由正切的定义,得
?
tan?????????????=??????????????????????????????????????????????????=??????????????????? =-1.
?
典型例题
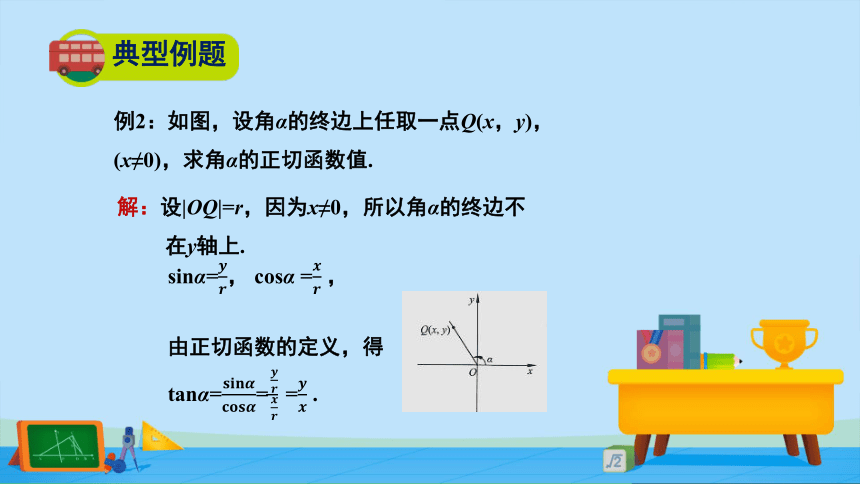
例2:如图,设角α的终边上任取一点Q(x,y),
(x≠0),求角α的正切函数值.
sinα=????????, cosα =???????? ,
由正切函数的定义,得
?
解:设|OQ|=r,因为x≠0,所以角α的终边不
在y轴上.
tanα=????????????????????????????????=???????????????? =???????? .
?
典型例题
通过例2,我们得到一个结论:若角α的终边上任取一点Q(x,y), (x≠0), 则
这个结论可以用来计算正切函数值.
tanα=???????? .
?
课文精讲
由正弦函数、余弦函数的诱导公式,对任意正数k,有
正切函数的诱导公式
tan(x+kπ) =????????????(????+????????)?????????????(????+????????)=
?
???????????????????????????????????=tanx,k为奇数,
?
?????????????????????????????????=tanx,k为偶数
?
即tan(x+kπ)?=tanx,其中x∈R,x≠??????????+kπ,k∈Z.
?
课文精讲
即tan(x+kπ)?=tanx,其中x∈R,x≠??????????+kπ,k∈Z.
?
所以kπ(k∈Z,k≠0)?是正切函数的周期,π是
它的最小正周期.
?
同时还可以得到
所以正切函数是奇函数.
tan(- x)=????????????(?????)?????????????(?????)= ?????????????????????????????????=? tanx
?
正切函数的诱导公式
课文精讲
思考
当?????????< α <????????时,角α与角-α,π+α,π-α, ????????+ α , ?????????α的正切函数值有什么关系?
?
正切函数的诱导公式
课文精讲
正切函数的诱导公式可由正弦函数、余弦函数相应的诱导公式得到:
tan(kπ+α)?=tanα (k∈Z)
tan(-α)?=?tanα
tan(π+α)?=tanα
tan(π-α)?=?tanα
tan??????????+????=??????????????????????
tan???????????????=?????????????????????
?
其中角α可以为使等式两边都有意义的任意角.
利用诱导公式,可将任意角的正切函数问题转化为锐角正切函数的问题.
正切函数的诱导公式
典型例题
例3: (1) tan??????????????????; (2) tan??????????????????; (3) tan ??????????????????.
?
解: (1) tan??????????????????= tan ?????????+?????????= tan?????????= ??????????;
(2) tan ???????????????????=? tan?????????????????=??tan ??????????+????????
=? tan??????????= tan ?????????= ??????????;
?
典型例题
例3: (1) tan??????????????????; (2) tan??????????????????; (3) tan ??????????????????.
?
解: (3)tan ??????????????????= ?tan?????????????????= ?tan ?????????+????????
=? tan ?????????= ??????????.
?
课文精讲
类比画正弦函数图象的方法,首先画出函数y= tanx,x∈ ?????????,????????的图象,再利用周期性将其延拓到整个定义域上,为此只需在区间???????,????????上取一系列的x值,例如, ????????? ,?????????, ?????????, ????, ????????, ????????, ????????.
?
正切函数的图象与性质
课文精讲
列表(如表).
正切函数的图象与性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
y=tanx
-1
0
1
课文精讲
利用表中的数据,先在平面直角坐标系内描点.然后用光滑曲线顺次连接,就可以得到函数y=tanx在区间?????????,????????上
的图象(如图).
?
正切函数的图象与性质
课文精讲
因为正切函数y=tanx是以π为周期的函数,所以它在区间??????????????????,?????????+????????上与在区间?????????,????????上的函数图象
形状完全相同.
?
正切函数的图象与性质
课文精讲
函数y=tanx,x∈?????????,????????的图象向左、右平移(每次平移π个单位长度),就可以得到正切函数y=tanx在
{x∈R|x≠?????????+????????,k∈Z}上
的图象(如图).正切函数的
图象称作正切曲线.
?
正切函数的图象与性质
课文精讲
从图可以看出,正切曲线是由被相互平行的直线x=????????+????????,k∈Z所隔开的无穷多支曲线组成的.这些直线称作正切曲线各支的渐近线.
?
正切函数的图象与性质
课文精讲
观察图,不难得出正切函数y=tanx的如下主要性质.
正切函数的图象与性质
1.定义域
正切函数的定义域是{x∈R|x≠?????????+????????,k∈Z}.
?
课文精讲
观察图,不难得出正切函数y=tanx的如下主要性质.
正切函数的图象与性质
2.值域
当x从左侧趋近????????+????????,k∈Z时,tanx趋近正无穷大;
当x从右侧趋近?????????+????????,k∈Z时,tanx趋近负无穷大.即y=tanx的值域是实数集R.
?
课文精讲
观察图,不难得出正切函数y=tanx的如下主要性质.
正切函数的图象与性质
3.周期性
正切函数是周期函数,周期是????????,k∈Z,k≠0,最小正周期是π.
?
课文精讲
观察图,不难得出正切函数y=tanx的如下主要性质.
正切函数的图象与性质
4.奇偶性
由tan(-x)=-tanx可知,正切函数是奇函数.正切曲线关于原点对称,(kπ,0)都是它的对称中心.
课文精讲
观察图,不难得出正切函数y=tanx的如下主要性质.
正切函数的图象与性质
5.单调性
正切函数在每一个区间?????????+?????????,?????????+????????,k∈Z上单调递增.
?
注:只能是开区间,因为x≠?????????+????????,k∈Z
?
课文精讲
“正切函数在其定义域内是增函数”这种说法是否正确?
正切函数的图象与性质
不正确.正切函数在定义域内不具备单调性,但在每一个开区间?????????+?????????,?????????+???????? k∈Z内是增函数.
?
课文精讲
由正切函数是奇函数,知它的图象关于原点对称.结合图象,你还能发现它的其他对称中心吗?有对称轴吗?
正切函数的图象与性质
正切函数的图象有无数个对称中心包括图象与x轴的交点和渐近线与x轴的交点.没有对称轴.
课文精讲
正切函数的图象与性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}函数
y=tanx
定义域
值域
R
周期性
周期函数,最小正周期为π
课文精讲
正切函数的图象与性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}函数
y=tanx
奇偶性
奇函数,图象关于原点对称
单调性
对称性
典型例题
例4:画出下列函数的图象,并求出定义域、周期和单调区间:
(1) tan2x; (2) tan??????????????.
?
解: (1)画出y= tan2x的图象如图(画法略).由y= tanx的定义域可知,函数y= tan2x的自变量x应满足2x≠????????+????????,k∈Z,
即x≠ ????????+????????????,k∈Z.
?
典型例题
例4:画出下列函数的图象,并求出定义域、周期和单调区间:
(1) tan2x; (2) tan??????????????.
?
解: (1) 所以函数y=tan2x的定义域是
{x∈R|x≠????????+????????????,k∈Z}.
?
典型例题
例4:画出下列函数的图象,并求出定义域、周期和单调区间:
(1) tan2x; (2) tan?????????????.
?
解: (1)由于y=tanx的周期是π,
tan2x=tan(2x+π )=tan2????+????????,因此,函
数y=tan2x的最
小正周期是????????.
?
典型例题
例4:画出下列函数的图象,并求出定义域、周期和单调区间:
(1) tan2x; (2) tan?????????????.
?
解: (1)因为y=tanx的单调递增区间是
?????????+?????????,?????????+????????,k∈Z.
?
所以由?????????+?????????<2x< ????????+
????????,k∈Z,解得??????????????????????<x< ????????????+????????,k∈Z.
?
典型例题
例4:画出下列函数的图象,并求出定义域、周期和单调区间:
(1) tan2x; (2) tan?????????????.
?
解: (1)因此,函数tan2x的单调递增区间是
?????????????????????,????????????+????????, k∈Z.
?
典型例题
例4:画出下列函数的图象,并求出定义域、周期和单调区间:
(1) tan2x; (2) tan?????????????.
?
解: (2)画出y=tan?????????????的图象如图(画法略).由y=tanx的定义域可知,函数y=tan?????????????的自变量x应满足?????????????≠ ????????+kπ,
k∈Z,即????≠????????????+kπ,
k∈Z.
?
典型例题
例4:画出下列函数的图象,并求出定义域、周期和单调区间:
(1) tan2x; (2) tan?????????????.
?
解: (2)因此,函数y=tan?????????????的定义域是
{x∈R|x≠????????????+????????,k∈Z}.
?
典型例题
例4:画出下列函数的图象,并求出定义域、周期和单调区间:
(1) tan2x; (2) tan?????????????.
?
解: (2)由于tan?????????????=tan?????????????+????
=tan(????+????)?????????,因此函数tan?????????????的
最小正周期是π.
?
典型例题
例4:画出下列函数的图象,并求出定义域、周期和单调区间:
(1) tan2x; (2) tan?????????????.
?
解: (2)由?????????????????<?????????????< ????????+????????,k∈Z,
解得??????????????????<x< ????????????+????????????,k∈Z.
?
因此,函数y=tan?????????????的单调递增区间是?????????????????,????????+????????????, k∈Z.
?
典型例题
例5:比较下列各组中三角函数值的大小:
tan ?????????????与tan ???????????? ;
tan?????????????????与tan?????????????????.
?
解: (1) tan ?????????????=? tan????????????=?tan ?????????+????
=? ?????????????????????=????????????????????.
?
tan????????????=tan ????????????+????=tan????????????.
?
典型例题
例5:比较下列各组中三角函数值的大小:
tan ?????????????与tan ???????????? ;
tan?????????????????与tan?????????????????.
?
解: (1)由于y= tanx在区间????,????????上单调递增,
且0<????????<????????????<????????,
因此tan ????????<tan ????????????,
即tan ?????????????< tan ???????????? .
?
典型例题
例5:比较下列各组中三角函数值的大小:
tan ?????????????与tan ???????????? ;
tan?????????????????与tan?????????????????.
?
解: (2) tan?????????????????=? tan????????????????=?tan????????+????????
=? tan????????,
tan?????????????????=? tan????????????????=?tan?????????????+????????
=??tan????????????.
?
典型例题
例5:比较下列各组中三角函数值的大小:
tan ?????????????与tan ???????????? ;
tan?????????????????与tan?????????????????.
?
解: (2)由于y= tanx在区间????,????????上单调递增,
且0<????????<????????????<????????,
因此tan ????????<tan ????????????,- tan ????????>- tan ????????????,
即tan??????????????????> tan????????????????? .
?
综合练习
已知2sin(α?????????)=sin(π+α),则tan(π-α)的值是______.
?
解: ∵2sin(α? ????????)=sin(π+α),
∴-2cosα =-sinα,可得tanα=2,
∴tan(π-α) =-tanα=-2.
故答案为:-2
?
-2
综合练习
已知角α的终边上一点A(????,?1),则tan(π+α)=______.
?
解:因为角α的终边上一点A(????,?1),
根据三角函数的定义,得tanα=? ,
所以tan(π+α)=tanα= .
?
?????????=??????????
?
??????????
?
??????????
?
本课小结
再 见
授课教师:
温故知新
学习目标
1. 理解正切函数的定义. (重点)
2.掌握正切函数的诱导公式,并能够灵活运用其进行化简求值. (重点)
3. 会画y=tanx的图象.(重点)
4.推导并理解正切函数在区间?????????,????????内的性质.(难点)
5.能够利用正切函数的性质解决有关问题. (难点)
?
课文精讲
正切函数的定义
根据函数的定义,比值????????????????????????????????是x的函数,称为x的正切函数,记作y=tanx,其中定义域为{x∈R|x≠?????????+kπ,k∈Z}.
当x∈ ?????,?????????时,上述定义与初中时所学正切函数的定义是一致的.
?
典型例题
例1:求下列角α的正切函数值:
(1) α=- ?????????; (2) α= ?????????????.
?
解: (1) 因为α=- ?????????,所以sin??????????=?????????? ,
cos??????????=?????????,由正切函数的定义,得
?
tan??????????=-????????????????????????????????????????????=??????????????????? =?1;
?
典型例题
例1:求下列角α的正切函数值:
(1) α=- ?????????; (2) α= ?????????????.
?
解: (2) 因为α=?????????????,所以sin ?????????????=????????? ,
cos?????????????=?????????? ,由正切的定义,得
?
tan?????????????=??????????????????????????????????????????????????=??????????????????? =-1.
?
典型例题
例2:如图,设角α的终边上任取一点Q(x,y),
(x≠0),求角α的正切函数值.
sinα=????????, cosα =???????? ,
由正切函数的定义,得
?
解:设|OQ|=r,因为x≠0,所以角α的终边不
在y轴上.
tanα=????????????????????????????????=???????????????? =???????? .
?
典型例题
通过例2,我们得到一个结论:若角α的终边上任取一点Q(x,y), (x≠0), 则
这个结论可以用来计算正切函数值.
tanα=???????? .
?
课文精讲
由正弦函数、余弦函数的诱导公式,对任意正数k,有
正切函数的诱导公式
tan(x+kπ) =????????????(????+????????)?????????????(????+????????)=
?
???????????????????????????????????=tanx,k为奇数,
?
?????????????????????????????????=tanx,k为偶数
?
即tan(x+kπ)?=tanx,其中x∈R,x≠??????????+kπ,k∈Z.
?
课文精讲
即tan(x+kπ)?=tanx,其中x∈R,x≠??????????+kπ,k∈Z.
?
所以kπ(k∈Z,k≠0)?是正切函数的周期,π是
它的最小正周期.
?
同时还可以得到
所以正切函数是奇函数.
tan(- x)=????????????(?????)?????????????(?????)= ?????????????????????????????????=? tanx
?
正切函数的诱导公式
课文精讲
思考
当?????????< α <????????时,角α与角-α,π+α,π-α, ????????+ α , ?????????α的正切函数值有什么关系?
?
正切函数的诱导公式
课文精讲
正切函数的诱导公式可由正弦函数、余弦函数相应的诱导公式得到:
tan(kπ+α)?=tanα (k∈Z)
tan(-α)?=?tanα
tan(π+α)?=tanα
tan(π-α)?=?tanα
tan??????????+????=??????????????????????
tan???????????????=?????????????????????
?
其中角α可以为使等式两边都有意义的任意角.
利用诱导公式,可将任意角的正切函数问题转化为锐角正切函数的问题.
正切函数的诱导公式
典型例题
例3: (1) tan??????????????????; (2) tan??????????????????; (3) tan ??????????????????.
?
解: (1) tan??????????????????= tan ?????????+?????????= tan?????????= ??????????;
(2) tan ???????????????????=? tan?????????????????=??tan ??????????+????????
=? tan??????????= tan ?????????= ??????????;
?
典型例题
例3: (1) tan??????????????????; (2) tan??????????????????; (3) tan ??????????????????.
?
解: (3)tan ??????????????????= ?tan?????????????????= ?tan ?????????+????????
=? tan ?????????= ??????????.
?
课文精讲
类比画正弦函数图象的方法,首先画出函数y= tanx,x∈ ?????????,????????的图象,再利用周期性将其延拓到整个定义域上,为此只需在区间???????,????????上取一系列的x值,例如, ????????? ,?????????, ?????????, ????, ????????, ????????, ????????.
?
正切函数的图象与性质
课文精讲
列表(如表).
正切函数的图象与性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}x
y=tanx
-1
0
1
课文精讲
利用表中的数据,先在平面直角坐标系内描点.然后用光滑曲线顺次连接,就可以得到函数y=tanx在区间?????????,????????上
的图象(如图).
?
正切函数的图象与性质
课文精讲
因为正切函数y=tanx是以π为周期的函数,所以它在区间??????????????????,?????????+????????上与在区间?????????,????????上的函数图象
形状完全相同.
?
正切函数的图象与性质
课文精讲
函数y=tanx,x∈?????????,????????的图象向左、右平移(每次平移π个单位长度),就可以得到正切函数y=tanx在
{x∈R|x≠?????????+????????,k∈Z}上
的图象(如图).正切函数的
图象称作正切曲线.
?
正切函数的图象与性质
课文精讲
从图可以看出,正切曲线是由被相互平行的直线x=????????+????????,k∈Z所隔开的无穷多支曲线组成的.这些直线称作正切曲线各支的渐近线.
?
正切函数的图象与性质
课文精讲
观察图,不难得出正切函数y=tanx的如下主要性质.
正切函数的图象与性质
1.定义域
正切函数的定义域是{x∈R|x≠?????????+????????,k∈Z}.
?
课文精讲
观察图,不难得出正切函数y=tanx的如下主要性质.
正切函数的图象与性质
2.值域
当x从左侧趋近????????+????????,k∈Z时,tanx趋近正无穷大;
当x从右侧趋近?????????+????????,k∈Z时,tanx趋近负无穷大.即y=tanx的值域是实数集R.
?
课文精讲
观察图,不难得出正切函数y=tanx的如下主要性质.
正切函数的图象与性质
3.周期性
正切函数是周期函数,周期是????????,k∈Z,k≠0,最小正周期是π.
?
课文精讲
观察图,不难得出正切函数y=tanx的如下主要性质.
正切函数的图象与性质
4.奇偶性
由tan(-x)=-tanx可知,正切函数是奇函数.正切曲线关于原点对称,(kπ,0)都是它的对称中心.
课文精讲
观察图,不难得出正切函数y=tanx的如下主要性质.
正切函数的图象与性质
5.单调性
正切函数在每一个区间?????????+?????????,?????????+????????,k∈Z上单调递增.
?
注:只能是开区间,因为x≠?????????+????????,k∈Z
?
课文精讲
“正切函数在其定义域内是增函数”这种说法是否正确?
正切函数的图象与性质
不正确.正切函数在定义域内不具备单调性,但在每一个开区间?????????+?????????,?????????+???????? k∈Z内是增函数.
?
课文精讲
由正切函数是奇函数,知它的图象关于原点对称.结合图象,你还能发现它的其他对称中心吗?有对称轴吗?
正切函数的图象与性质
正切函数的图象有无数个对称中心包括图象与x轴的交点和渐近线与x轴的交点.没有对称轴.
课文精讲
正切函数的图象与性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}函数
y=tanx
定义域
值域
R
周期性
周期函数,最小正周期为π
课文精讲
正切函数的图象与性质
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}函数
y=tanx
奇偶性
奇函数,图象关于原点对称
单调性
对称性
典型例题
例4:画出下列函数的图象,并求出定义域、周期和单调区间:
(1) tan2x; (2) tan??????????????.
?
解: (1)画出y= tan2x的图象如图(画法略).由y= tanx的定义域可知,函数y= tan2x的自变量x应满足2x≠????????+????????,k∈Z,
即x≠ ????????+????????????,k∈Z.
?
典型例题
例4:画出下列函数的图象,并求出定义域、周期和单调区间:
(1) tan2x; (2) tan??????????????.
?
解: (1) 所以函数y=tan2x的定义域是
{x∈R|x≠????????+????????????,k∈Z}.
?
典型例题
例4:画出下列函数的图象,并求出定义域、周期和单调区间:
(1) tan2x; (2) tan?????????????.
?
解: (1)由于y=tanx的周期是π,
tan2x=tan(2x+π )=tan2????+????????,因此,函
数y=tan2x的最
小正周期是????????.
?
典型例题
例4:画出下列函数的图象,并求出定义域、周期和单调区间:
(1) tan2x; (2) tan?????????????.
?
解: (1)因为y=tanx的单调递增区间是
?????????+?????????,?????????+????????,k∈Z.
?
所以由?????????+?????????<2x< ????????+
????????,k∈Z,解得??????????????????????<x< ????????????+????????,k∈Z.
?
典型例题
例4:画出下列函数的图象,并求出定义域、周期和单调区间:
(1) tan2x; (2) tan?????????????.
?
解: (1)因此,函数tan2x的单调递增区间是
?????????????????????,????????????+????????, k∈Z.
?
典型例题
例4:画出下列函数的图象,并求出定义域、周期和单调区间:
(1) tan2x; (2) tan?????????????.
?
解: (2)画出y=tan?????????????的图象如图(画法略).由y=tanx的定义域可知,函数y=tan?????????????的自变量x应满足?????????????≠ ????????+kπ,
k∈Z,即????≠????????????+kπ,
k∈Z.
?
典型例题
例4:画出下列函数的图象,并求出定义域、周期和单调区间:
(1) tan2x; (2) tan?????????????.
?
解: (2)因此,函数y=tan?????????????的定义域是
{x∈R|x≠????????????+????????,k∈Z}.
?
典型例题
例4:画出下列函数的图象,并求出定义域、周期和单调区间:
(1) tan2x; (2) tan?????????????.
?
解: (2)由于tan?????????????=tan?????????????+????
=tan(????+????)?????????,因此函数tan?????????????的
最小正周期是π.
?
典型例题
例4:画出下列函数的图象,并求出定义域、周期和单调区间:
(1) tan2x; (2) tan?????????????.
?
解: (2)由?????????????????<?????????????< ????????+????????,k∈Z,
解得??????????????????<x< ????????????+????????????,k∈Z.
?
因此,函数y=tan?????????????的单调递增区间是?????????????????,????????+????????????, k∈Z.
?
典型例题
例5:比较下列各组中三角函数值的大小:
tan ?????????????与tan ???????????? ;
tan?????????????????与tan?????????????????.
?
解: (1) tan ?????????????=? tan????????????=?tan ?????????+????
=? ?????????????????????=????????????????????.
?
tan????????????=tan ????????????+????=tan????????????.
?
典型例题
例5:比较下列各组中三角函数值的大小:
tan ?????????????与tan ???????????? ;
tan?????????????????与tan?????????????????.
?
解: (1)由于y= tanx在区间????,????????上单调递增,
且0<????????<????????????<????????,
因此tan ????????<tan ????????????,
即tan ?????????????< tan ???????????? .
?
典型例题
例5:比较下列各组中三角函数值的大小:
tan ?????????????与tan ???????????? ;
tan?????????????????与tan?????????????????.
?
解: (2) tan?????????????????=? tan????????????????=?tan????????+????????
=? tan????????,
tan?????????????????=? tan????????????????=?tan?????????????+????????
=??tan????????????.
?
典型例题
例5:比较下列各组中三角函数值的大小:
tan ?????????????与tan ???????????? ;
tan?????????????????与tan?????????????????.
?
解: (2)由于y= tanx在区间????,????????上单调递增,
且0<????????<????????????<????????,
因此tan ????????<tan ????????????,- tan ????????>- tan ????????????,
即tan??????????????????> tan????????????????? .
?
综合练习
已知2sin(α?????????)=sin(π+α),则tan(π-α)的值是______.
?
解: ∵2sin(α? ????????)=sin(π+α),
∴-2cosα =-sinα,可得tanα=2,
∴tan(π-α) =-tanα=-2.
故答案为:-2
?
-2
综合练习
已知角α的终边上一点A(????,?1),则tan(π+α)=______.
?
解:因为角α的终边上一点A(????,?1),
根据三角函数的定义,得tanα=? ,
所以tan(π+α)=tanα= .
?
?????????=??????????
?
??????????
?
??????????
?
本课小结
再 见
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
