2.1.2向量的基本关系-【新教材】2020-2021学年北师大版(2019)高中数学必修第二册课件(27张PPT)
文档属性
| 名称 | 2.1.2向量的基本关系-【新教材】2020-2021学年北师大版(2019)高中数学必修第二册课件(27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 850.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 00:00:00 | ||
图片预览






文档简介
向量的基本关系
授课教师:
温故知新
学习目标
1.理解平行向量、共线向量、相等向量的概念;(重点)
2. 能够能够掌握它们之间的联系与区别.(难点)
课文精讲
导入
思考
上体育课时,当某一排同学整理好队形,并
执行完老师的口令“向前三步走,向右看齐”之后,同学们位移的方向是否相同?位移的大小是否相等?能否认为同学们的位移是相同的?
可以认为,情境中同学们位移的方向和大小都相等,即位移相同.
课文精讲
在物理学中,两个物体运动速度相等是指它们的方向相同、大小相等;两个力相等不仅
包括方向相同、大小相等,还包括作用点相同.
相等向量
课文精讲
相等向量
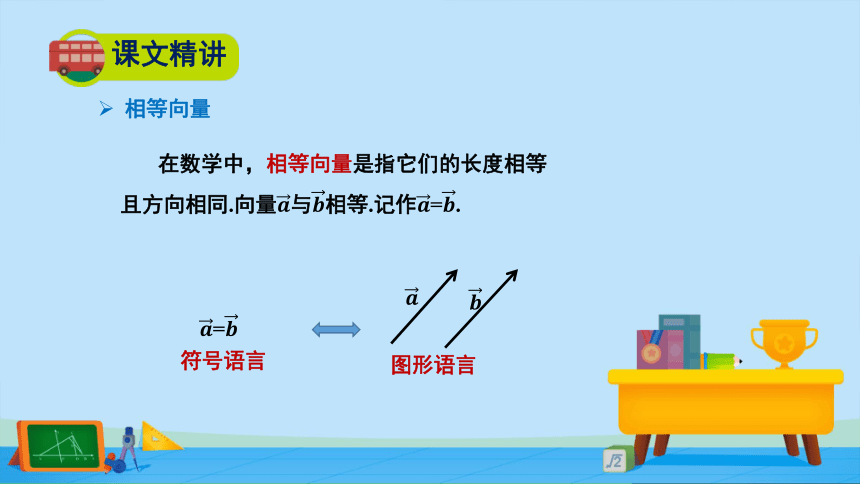
在数学中,相等向量是指它们的长度相等且方向相同.向量????与????相等.记作????=????.
?
符号语言
图形语言
????=????
?
????
?
????
?
课文精讲
若两条有向线段方向相同、长度相等,则它们表示的向量是相等的.代表相等向量的有向线段与起点位置无关.直观地说,一条有向线段在平移过程中,虽然位置不同,但表示的是相等向量.
相等向量
课文精讲
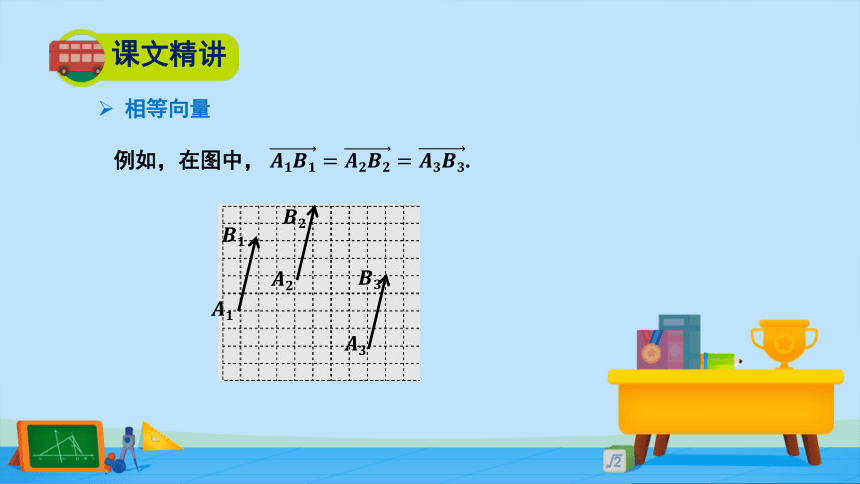
例如,在图中, ????????????????=????????????????=????????????????.
?
相等向量
????????
?
????????
?
????????
?
????????
?
????????
?
????????
?
课文精讲
相等向量
(1)相等向量有无数多个,它们可以通过平移重合
在一起,当两个相等向量起点重合时,终点一
定重合;
(2)模相等是向量相等的必要条件,模相等且方向
相同是向量相等的充分条件;
(3)相等向量,满足传递性,即若????=????且????=????,则
????=????.
?
思考:如何理解相等向量?
课文精讲
共线向量
若两个非零向量????,????的方向相同或相反(如图),则称这两个向量为共线向量或平行向量,也称这两个向量共线或平行,记作?????// ????.
?
两个向量共线或平行,是指表示这两个向量的有向线段所在的直线重合或平行.
课文精讲
共线向量
若两个向量的长度相等、方向相反,则称它们互为相反向量.相反向量是共线向量.若其中一个向量为?????,则它的相反向量记作- ????.
?
规定零向量与任一向量共线,即对于任意的向量?????,都有?????∥ ????.零向量的相反向量仍是零向量.
?
课文精讲
共线向量
(1)共线向量只考虑方向(相同或相反),而相等向量既考虑方向又考虑模(方向相同,模相等);
(2)相等向量一定是共线向量,但共线向量不一定是相等向量.
思考:共线向量与相等向量之间的关系是什么?
典型例题
例1:如图,点D,E,F分别是等边三角形ABC
的边AB,BC,AC的中点.在以点A,B,C,D,
E,F为起点或终点的向量中:
(1)找出与向量 ????????相等的向量;
(2)找出与向量 ????????共线的向量.
?
解:根据三角形的中位线定理,得
(1)在以点A,B,C,D,E,F为起点或终点的
向量中,与向量 ????????相等的向量有: ????????和????????.
?
A
B
C
E
D
F
典型例题
例1:如图,点D,E,F分别是等边三角形ABC
的边AB,BC,AC的中点.在以点A,B,C,D,
E,F为起点或终点的向量中:
(1)找出与向量 ????????相等的向量;
(2)找出与向量 ????????共线的向量.
?
解: (2)在以点A,B,C,D,E,F为起点或终
点的向量中,与向量????????共线的向量有
????????, ????????, ????????, ????????, ????????, ????????, ???????? .
?
A
B
C
E
D
F
课文精讲
己知两个零向量????和????.如图,在平面内选一
点O,作?????????= ?????, ????????=???? ,则θ=∠AOB(0°≤ θ
≤180°)称为向量????与????的夹角.
?
共线向量
????
?
?????
?
????
?
?????
?
????
?
????
?
A
θ
课文精讲
当θ =0°时, ????与????同向,当θ =180°时,
????与????反向,当θ =90°时,????与????垂直,记作????⊥????.
规定零向量可与任一向量垂直,即对于任
意的向量????,都有????⊥????.
?
共线向量
????
?
?????
?
????
?
?????
?
????
?
????
?
A
θ
典型例题
例3:如图,等边三角形ABC中,点D,E,F分
别是边AB,BC,AC的中点,指出如下各组向量的夹角.
(1) ????????与????????;(2) ) ????????与????????;(3) ) ????????与????????.
?
解: (1) ????????与????????的夹角是∠EDF=60°;
?
A
B
C
E
D
F
(1)
典型例题
解: (2) 因为????????= ???????? ,所以????????与???????? 的夹角等于
????????与???????? 的夹角,
即∠EDA=120°;
?
A
B
C
E
D
F
(1)
例3:如图,等边三角形ABC中,点D,E,F分
别是边AB,BC,AC的中点,指出如下各组向量的夹角.
(1) ????????与????????;(2) ) ????????与????????;(3) ) ????????与????????.
?
典型例题
解: (3) 如图(2) ,延长FD至B′,使DB′=FD,
则????????′ = ???????? ,则????????与????????的夹角等于
????????与 ????????′的夹角,
即∠EDB′=120°.
?
A
B
C
E
D
F
(2)
B′
例3:如图,等边三角形ABC中,点D,E,F分
别是边AB,BC,AC的中点,指出如下各组向量的夹角.
(1) ????????与????????;(2) ) ????????与????????;(3) ) ????????与????????.
?
综合练习
已知向量????,????,???? 满足????∥????, ????∥????,则????∥????
一定平行吗?
?
忽视零向量致误
解:分两种情况说明:
①当向量????= ????,向量????与向量????均为非零向量时,不能保证????∥????.
?
综合练习
已知向量????,????,???? 满足????∥????, ????∥????,则????∥????
一定平行吗?
?
解:②当向量????≠????时,因为????∥?????,所以向量????与
向量????具有相同或相反方向.又因为????∥????,所
以向量????与向量????具有相同或相反方向,所
以向量????与向量???? 满足具有相同或相反方向,
故????∥????.
?
忽视零向量致误
综合练习
已知向量????,????,???? 满足????∥????, ????∥????,则????∥????
一定平行吗?
?
忽视零向量致误
解:②综上所述,当向量????≠ ????时,向量????与向量???? 平行;当向量????= ????时,向量????与向量????不一定平行.
?
综合练习
忽视零向量致误
注意:求解向量问题时,要注意题目中的向量能否为零向量.零向量是特殊的向量,方向是任意的. 所有的零向量都相等.零向量的起点与终点是同一点,故不能用有向线段表示出来.
综合练习
对共线向量理解错误
若向量????????与????????是共线向量,则四点A,B,C,D必在同一条直线上.这种说法是否正确?为什么?
?
解:不正确.因为向量可以自由平移,所以点
A,B,C,D不一定在同一条直线上.
综合练习
对共线向量理解错误
注意:因为向量可以自由平移,因此,共线向量所在的直线可以平行,也可以重合,不能与平行直线混淆.
本课小结
再 见
授课教师:
温故知新
学习目标
1.理解平行向量、共线向量、相等向量的概念;(重点)
2. 能够能够掌握它们之间的联系与区别.(难点)
课文精讲
导入
思考
上体育课时,当某一排同学整理好队形,并
执行完老师的口令“向前三步走,向右看齐”之后,同学们位移的方向是否相同?位移的大小是否相等?能否认为同学们的位移是相同的?
可以认为,情境中同学们位移的方向和大小都相等,即位移相同.
课文精讲
在物理学中,两个物体运动速度相等是指它们的方向相同、大小相等;两个力相等不仅
包括方向相同、大小相等,还包括作用点相同.
相等向量
课文精讲
相等向量
在数学中,相等向量是指它们的长度相等且方向相同.向量????与????相等.记作????=????.
?
符号语言
图形语言
????=????
?
????
?
????
?
课文精讲
若两条有向线段方向相同、长度相等,则它们表示的向量是相等的.代表相等向量的有向线段与起点位置无关.直观地说,一条有向线段在平移过程中,虽然位置不同,但表示的是相等向量.
相等向量
课文精讲
例如,在图中, ????????????????=????????????????=????????????????.
?
相等向量
????????
?
????????
?
????????
?
????????
?
????????
?
????????
?
课文精讲
相等向量
(1)相等向量有无数多个,它们可以通过平移重合
在一起,当两个相等向量起点重合时,终点一
定重合;
(2)模相等是向量相等的必要条件,模相等且方向
相同是向量相等的充分条件;
(3)相等向量,满足传递性,即若????=????且????=????,则
????=????.
?
思考:如何理解相等向量?
课文精讲
共线向量
若两个非零向量????,????的方向相同或相反(如图),则称这两个向量为共线向量或平行向量,也称这两个向量共线或平行,记作?????// ????.
?
两个向量共线或平行,是指表示这两个向量的有向线段所在的直线重合或平行.
课文精讲
共线向量
若两个向量的长度相等、方向相反,则称它们互为相反向量.相反向量是共线向量.若其中一个向量为?????,则它的相反向量记作- ????.
?
规定零向量与任一向量共线,即对于任意的向量?????,都有?????∥ ????.零向量的相反向量仍是零向量.
?
课文精讲
共线向量
(1)共线向量只考虑方向(相同或相反),而相等向量既考虑方向又考虑模(方向相同,模相等);
(2)相等向量一定是共线向量,但共线向量不一定是相等向量.
思考:共线向量与相等向量之间的关系是什么?
典型例题
例1:如图,点D,E,F分别是等边三角形ABC
的边AB,BC,AC的中点.在以点A,B,C,D,
E,F为起点或终点的向量中:
(1)找出与向量 ????????相等的向量;
(2)找出与向量 ????????共线的向量.
?
解:根据三角形的中位线定理,得
(1)在以点A,B,C,D,E,F为起点或终点的
向量中,与向量 ????????相等的向量有: ????????和????????.
?
A
B
C
E
D
F
典型例题
例1:如图,点D,E,F分别是等边三角形ABC
的边AB,BC,AC的中点.在以点A,B,C,D,
E,F为起点或终点的向量中:
(1)找出与向量 ????????相等的向量;
(2)找出与向量 ????????共线的向量.
?
解: (2)在以点A,B,C,D,E,F为起点或终
点的向量中,与向量????????共线的向量有
????????, ????????, ????????, ????????, ????????, ????????, ???????? .
?
A
B
C
E
D
F
课文精讲
己知两个零向量????和????.如图,在平面内选一
点O,作?????????= ?????, ????????=???? ,则θ=∠AOB(0°≤ θ
≤180°)称为向量????与????的夹角.
?
共线向量
????
?
?????
?
????
?
?????
?
????
?
????
?
A
θ
课文精讲
当θ =0°时, ????与????同向,当θ =180°时,
????与????反向,当θ =90°时,????与????垂直,记作????⊥????.
规定零向量可与任一向量垂直,即对于任
意的向量????,都有????⊥????.
?
共线向量
????
?
?????
?
????
?
?????
?
????
?
????
?
A
θ
典型例题
例3:如图,等边三角形ABC中,点D,E,F分
别是边AB,BC,AC的中点,指出如下各组向量的夹角.
(1) ????????与????????;(2) ) ????????与????????;(3) ) ????????与????????.
?
解: (1) ????????与????????的夹角是∠EDF=60°;
?
A
B
C
E
D
F
(1)
典型例题
解: (2) 因为????????= ???????? ,所以????????与???????? 的夹角等于
????????与???????? 的夹角,
即∠EDA=120°;
?
A
B
C
E
D
F
(1)
例3:如图,等边三角形ABC中,点D,E,F分
别是边AB,BC,AC的中点,指出如下各组向量的夹角.
(1) ????????与????????;(2) ) ????????与????????;(3) ) ????????与????????.
?
典型例题
解: (3) 如图(2) ,延长FD至B′,使DB′=FD,
则????????′ = ???????? ,则????????与????????的夹角等于
????????与 ????????′的夹角,
即∠EDB′=120°.
?
A
B
C
E
D
F
(2)
B′
例3:如图,等边三角形ABC中,点D,E,F分
别是边AB,BC,AC的中点,指出如下各组向量的夹角.
(1) ????????与????????;(2) ) ????????与????????;(3) ) ????????与????????.
?
综合练习
已知向量????,????,???? 满足????∥????, ????∥????,则????∥????
一定平行吗?
?
忽视零向量致误
解:分两种情况说明:
①当向量????= ????,向量????与向量????均为非零向量时,不能保证????∥????.
?
综合练习
已知向量????,????,???? 满足????∥????, ????∥????,则????∥????
一定平行吗?
?
解:②当向量????≠????时,因为????∥?????,所以向量????与
向量????具有相同或相反方向.又因为????∥????,所
以向量????与向量????具有相同或相反方向,所
以向量????与向量???? 满足具有相同或相反方向,
故????∥????.
?
忽视零向量致误
综合练习
已知向量????,????,???? 满足????∥????, ????∥????,则????∥????
一定平行吗?
?
忽视零向量致误
解:②综上所述,当向量????≠ ????时,向量????与向量???? 平行;当向量????= ????时,向量????与向量????不一定平行.
?
综合练习
忽视零向量致误
注意:求解向量问题时,要注意题目中的向量能否为零向量.零向量是特殊的向量,方向是任意的. 所有的零向量都相等.零向量的起点与终点是同一点,故不能用有向线段表示出来.
综合练习
对共线向量理解错误
若向量????????与????????是共线向量,则四点A,B,C,D必在同一条直线上.这种说法是否正确?为什么?
?
解:不正确.因为向量可以自由平移,所以点
A,B,C,D不一定在同一条直线上.
综合练习
对共线向量理解错误
注意:因为向量可以自由平移,因此,共线向量所在的直线可以平行,也可以重合,不能与平行直线混淆.
本课小结
再 见
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
