2.2.1向量的加法-【新教材】2020-2021学年北师大版(2019)高中数学必修第二册课件(42张PPT)
文档属性
| 名称 | 2.2.1向量的加法-【新教材】2020-2021学年北师大版(2019)高中数学必修第二册课件(42张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 00:00:00 | ||
图片预览







文档简介
向量的加法
授课教师:
温故知新
学习目标
1.理解并掌握向量加法的概念,了解向量加法的
几何意义及其运算律;(重点)
2.掌握向量加法运算法则,能熟练进行加法运算;(难点)
3.掌握数的加法与向量的加法的联系与区别.
课文精讲
向量加法的定义
天车是大型生产车间或工地进行起重作业
的重要设备.如图,物体在天车的作用下,同时
进行竖直方向的位移和水平方向的位移.实际位
移 ????????可以看作竖直方向的位移????????与水平方向的
位移 ????????的合成.
?
课文精讲
向量加法的定义
求两个向量和的运算,称为向量????的加法.
?
课文精讲
向量加法的定义
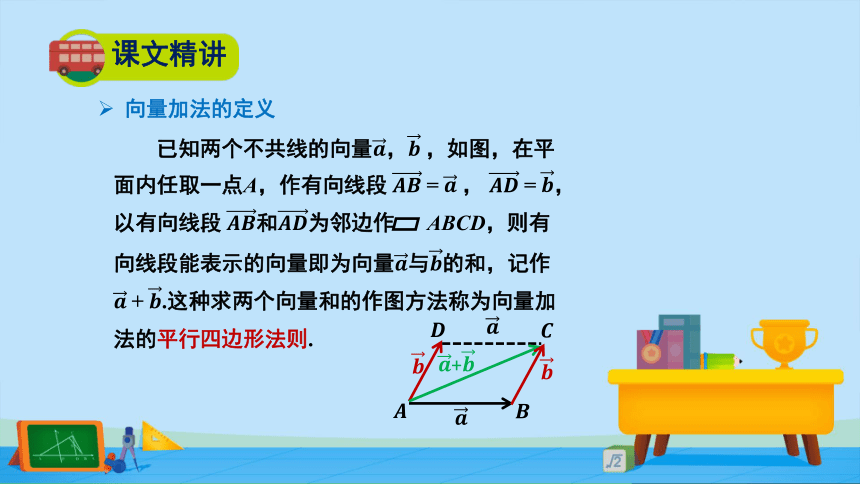
已知两个不共线的向量????,?????,如图,在平
面内任取一点A,作有向线段 ?????????= ???? , ?????????= ????,
以有向线段 ????????和????????为邻边作 ABCD,则有
向线段能表示的向量即为向量????与????的和,记作
?????+ ????.这种求两个向量和的作图方法称为向量加
法的平行四边形法则.
?
????
?
????
?
????+????
?
????
?
????
?
????
?
????
?
????
?
????
?
课文精讲
向量加法的定义
????
?
????
?
????+????
?
????
?
????
?
????
?
????
?
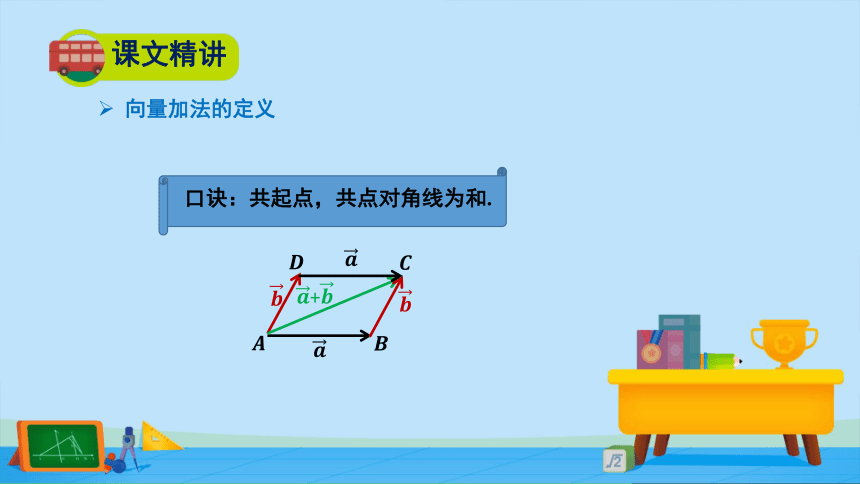
口诀:共起点,共点对角线为和.
????
?
????
?
课文精讲
显然,如图,作有向线段?????????= ???? , 以有向线段????????的终点为起点,作有向线段 ?????????= ????.
连接A,C得到有向线段????????,也可以表示向量????与????的和.这种求两个向量和的作图方法称为向量加法的三角形法则.
?
向量加法的定义
????
?
????
?
????+?????
?
C
B
A
课文精讲
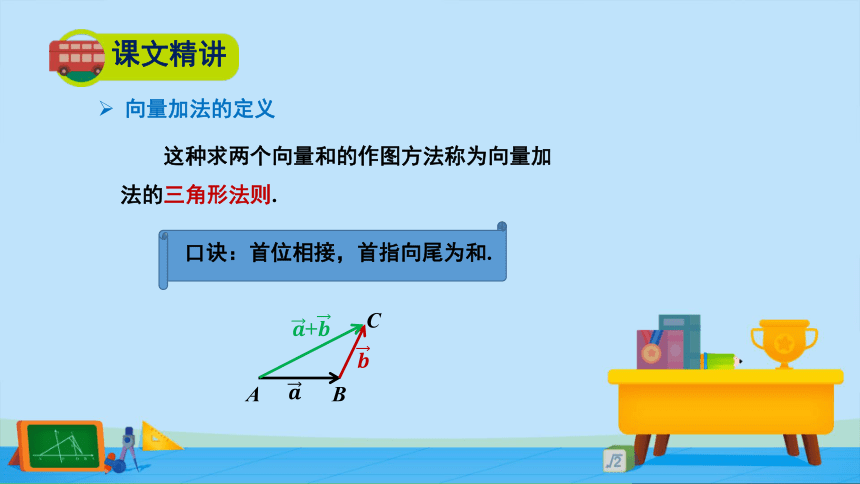
这种求两个向量和的作图方法称为向量加法的三角形法则.
向量加法的定义
????
?
????
?
????+?????
?
C
B
A
口诀:首位相接,首指向尾为和.
课文精讲
向量加法的平行四边形法则与三角形法则一致吗?为什么?
向量加法的定义
(1) 两个法则的使用条件不同.
三角形法则适用于任意两个非零向量求和,平行四边形法则只适用于两个不共线的向量求和.
课文精讲
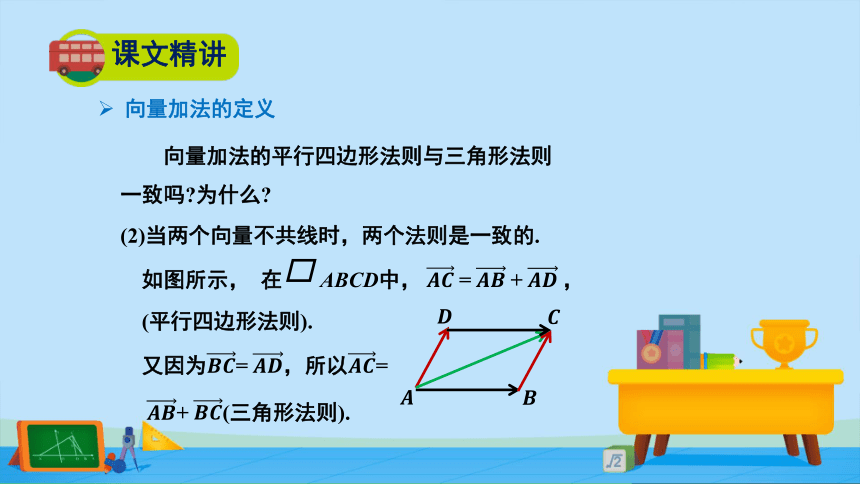
向量加法的平行四边形法则与三角形法则一致吗?为什么?
向量加法的定义
(2)当两个向量不共线时,两个法则是一致的.
如图所示, 在 ABCD中, ?????????= ?????????+ ?????????,
(平行四边形法则).
又因为????????= ????????,所以????????=
????????+ ????????(三角形法则).
?
????
?
????
?
????
?
????
?
课文精讲
向量加法的定义
思考:两个向量相加就是两个向量的模相加吗?
不是.因为向量既有大小,又有方向,
所以两个向量相加不是模相加,两个向量
相加应满足向量加法的三角形法则或平行
四边形法则.
课文精讲
若????,????共线,如图表示了两个共线向量求和的情形.
?
向量加法的定义
????
?
????
?
????
?
????
?
????+????
?
????
?
????
?
????+????
?
????
?
????
?
(1) (2)
课文精讲
若两个共线向量方向相同,则它们的和向量方向与原方向一致,大小为两个向量大小之和(如图(1));
向量加法的定义
????
?
????
?
????
?
????
?
????+????
?
(1)
课文精讲
若两个共线向量方向相反且大小不相等,则它们的和向量方向与较大向量的方向一致,大小是两个向量大小差的绝对值(如图(2)).
向量加法的定义
????
?
????
?
????+????
?
????
?
????
?
(2)
课文精讲
由向量加法的定义可知,互为相反向量的两个向量的和为零向量,即
?????+(- ????)=(- ????)+ ?????= ????.
?
向量加法的定义
典型例题
例1:如图,已知向量????,????,求作向量????+????.
?
解:作法1(平行四边形法则):如图在平面内任
取一点O,作????????= ????, ????????= ????,以OA,OB
为邻边作 OBCA,则????????=????+????.
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
典型例题
例1:如图,已知向量????,????,求作向量????+????.
?
解:作法2(三角形法则):如图在平面内任取一点O,作????????= ????, ????????= ????, ,则????????= ????+????.
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
课文精讲
思考
对任意的两个向量????,????,| ????+????|,|????|+|????|,
|????|-|????|之间具有怎样的大小关系?通过作图进行
解释.
?
向量加法的定义
||????|-|????||≤|????+????|≤|????|+|????|
?
????
?
????
?
????+?????
?
C
B
A
课文精讲
思考
对任意的两个向量????,????,| ????+????|,|????|+|????|,
|????|-|????|之间具有怎样的大小关系?通过作图进行
解释.
?
向量加法的定义
由上可看出,向量????,????的模与????+????的模之
间满足不等式
||????|-|????||≤|????+????|≤|????|+|????|
?
(向量形式的三角不等式)
课文精讲
点拨:利用向量形式的三角不等式可以解决有关向量的大小(模)的取值范围或最值问题,但需注意验证等号成立的条件,即当????与????同向时, |????+????|=|????|+|????| .
?
向量加法的定义
||????|-|????||≤|????+????|≤|????|+|????|
?
????
?
????
?
????+?????
?
C
B
A
典型例题
例2:轮船从A港沿北偏东60°方向行驶了40
n mile到达B处,再由B处沿正北方向行驶40
n mile到达C处.求此时轮船与A港的相对位置.
解:如图, ????????, ????????分别表示轮船的两次位移,
则 ????????表示轮船的合位移, ?????????= ?????????+ ????????.
设正东方向所在直线为AE,
过点B作AE的垂线,垂足为
点D.
?
典型例题
解:在Rt△ADB中,∠ADB=90°,
∠DAB=30°,|????????|=40 n mile,
所以 |????????|=|????????|·sin ∠DAB
=40·sin30°
=20(n mile).
?
例2:轮船从A港沿北偏东60°方向行驶了40
n mile到达B处,再由B处沿正北方向行驶40
n mile到达C处.求此时轮船与A港的相对位置.
典型例题
解:|????????|=|????????|·cos ∠DAB
=40·cos30°
=20????(n mile).
?
例2:轮船从A港沿北偏东60°方向行驶了40
n mile到达B处,再由B处沿正北方向行驶40
n mile到达C处.求此时轮船与A港的相对位置.
典型例题
解:在Rt△ADB中,∠ADC=90°, |????????|=|????????|+ |????????|=60 (n mile),由勾股定理得|????????|=|????????|????+|????????|????
= (????????????)????+????????????
= 40 ???? (n mile).
?
例2:轮船从A港沿北偏东60°方向行驶了40
n mile到达B处,再由B处沿正北方向行驶40
n mile到达C处.求此时轮船与A港的相对位置.
典型例题
解:由|????????|=2 |????????|,得∠CAD=60°.
因此,此时轮船位于A港北偏东30°,且
距A港40 ????的C处.
?
例2:轮船从A港沿北偏东60°方向行驶了40
n mile到达B处,再由B处沿正北方向行驶40
n mile到达C处.求此时轮船与A港的相对位置.
课文精讲
问题提出
我们熟知,数的加法满足结合律和交换
律,即对任意α,β,γ∈R,有
(α+β)+ γ= α+(β+γ)
α+β=β+α
那么向最的加法运算满足哪些运算律呢?
向量加法的运算律
课文精讲
分析理解
向量的加法也满足结合律和交换律,即
(????+????)+????=????+(????+????)
????+????=????+????
?
向量加法的运算律
结合律
交换律
课文精讲
分析理解
先证明向量????,????,????的加法满足结合律.
由图可知
(????+????)+????= (????????+????????)+????????= ????????+????????=????????,
????+ (????+????)= ????????+(????????+????????)= ????????+?????????= ????????.
所以 (????+????)+????=????+(????+????)
?
向量加法的运算律
结合律
????
?
????+????
?
????
?
????
?
????
?
????
?
????
?
????+????
?
????+????+????
?
????
?
课文精讲
分析理解
再证明向量????,????的加法满足交换律.由图
可知
????+????= ????????+????????= ????????,
????+????= ????????+????????=????????.
所以 ????+????=????+????
?
向量加法的运算律
交换律
????
?
????
?
????+????
?
????
?
????
?
????
?
????
?
????
?
????
?
课文精讲
多个向量的加法运算可按照任意的次序
与任意的组合进行,如
(????+????)+(????+????)=(????+????)+(????+????);
????+????+????+????+????=[????+(????+????)]+(????+????).
?
向量加法的运算律
典型例题
例3:如图,已知向量????,????,?????, ????,作出????+
????+?????+?????,并说明多个向量求和的方法及依据.
?
解:可以按照不同的次序与组合
进行这四个向量的加法.
????
?
????
?
????
?
????
?
典型例题
例3:如图,已知向量????,????,?????, ????,作出????+
????+?????+?????,并说明多个向量求和的方法及依据.
?
解:方法1
如图,在平面上任取一点A,
作????????=????,????????=????, ????????= ?????,
????????=????,
????+????+?????+?????=[(????+????)+ ????]+ ?????
=(????????+????)+ ?????= ????????+ ?????= ????????.
?
????
?
????
?
????
?
????
?
????
?
????+????+?????+????
?
????
?
????
?
????
?
A
C
B
D
E
典型例题
例3:如图,已知向量????,????,?????, ????,作出????+
????+?????+?????,并说明多个向量求和的方法及依据.
?
解:方法2
如图,在平面上任取一点A′,
作????′????′=????,????′????′=????, ????′????′= ?????, ????′????′=????,则
????+????+?????+?????=(????+????)+( ????+ ????)
=????′????′+????′????′= ????′????′.
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????+????+?????+?????
?
A′
C′
B′
D′
E′
课文精讲
由于向量的加法满足结合律与交换律,
因此求n个向量????????, ????????, ···, ????????,的和可
以按以下步骤进行:
任取一点O,依次作有向线段?????????????=????????,
?????????????????=????????, ···, ??????????????????????= ????????, ????????????即为
这n个向量之和.
?
当然,也可以把n个向量分为若干组,
先求每组向量之和,再求出这些组向量和的
和.
课文精讲
另外,为了得到有限个向量的和,只需将
这些向量依次首尾相接,那么以第一个向量的
始点为始点,最后一个向量的终点为终点的向
量,就是这些向量的和,如图所示.
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????+????+????+????+????
?
课文精讲
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????+????+????+????+????
?
图中的和,与向量相加的顺序有关吗?为
什么?
无关,因为向量相加满足交换律
综合练习
化简下列各式:
(1)????????+????????+????????; (2)????????+????????+????????+????????+????????.
?
解:(1)????????+????????+????????
=(????????+????????)+????????
=????????+????????
=????????.
?
综合练习
化简下列各式:
(1)????????+????????+????????; (2)????????+????????+????????+????????+????????.
?
解: (2)????????+????????+????????+????????+????????
=????????+????????+(????????+????????+????????)
=????????+????????+????????
=(????????+????????)+????????
=????????+????????
=????????=????.
?
综合练习
已知|????|=3, |????|=4,求|????+????|的最大值和最小值,并说明取得最大值和最小值时 ????与????的关系.
?
解:由|????+????|≤|????|+|????|
可知, |????+????|的最大值为|????|+|????| =3+4=7.
当且仅当????与????方向相同时取得最大值.
由|????+????| ≥||????|-|????||,可知|????+????|的最小值为||????|-|????||=|3-4|=1.
当且仅当与方向相反时取得最小值.
?
本课小结
再 见
授课教师:
温故知新
学习目标
1.理解并掌握向量加法的概念,了解向量加法的
几何意义及其运算律;(重点)
2.掌握向量加法运算法则,能熟练进行加法运算;(难点)
3.掌握数的加法与向量的加法的联系与区别.
课文精讲
向量加法的定义
天车是大型生产车间或工地进行起重作业
的重要设备.如图,物体在天车的作用下,同时
进行竖直方向的位移和水平方向的位移.实际位
移 ????????可以看作竖直方向的位移????????与水平方向的
位移 ????????的合成.
?
课文精讲
向量加法的定义
求两个向量和的运算,称为向量????的加法.
?
课文精讲
向量加法的定义
已知两个不共线的向量????,?????,如图,在平
面内任取一点A,作有向线段 ?????????= ???? , ?????????= ????,
以有向线段 ????????和????????为邻边作 ABCD,则有
向线段能表示的向量即为向量????与????的和,记作
?????+ ????.这种求两个向量和的作图方法称为向量加
法的平行四边形法则.
?
????
?
????
?
????+????
?
????
?
????
?
????
?
????
?
????
?
????
?
课文精讲
向量加法的定义
????
?
????
?
????+????
?
????
?
????
?
????
?
????
?
口诀:共起点,共点对角线为和.
????
?
????
?
课文精讲
显然,如图,作有向线段?????????= ???? , 以有向线段????????的终点为起点,作有向线段 ?????????= ????.
连接A,C得到有向线段????????,也可以表示向量????与????的和.这种求两个向量和的作图方法称为向量加法的三角形法则.
?
向量加法的定义
????
?
????
?
????+?????
?
C
B
A
课文精讲
这种求两个向量和的作图方法称为向量加法的三角形法则.
向量加法的定义
????
?
????
?
????+?????
?
C
B
A
口诀:首位相接,首指向尾为和.
课文精讲
向量加法的平行四边形法则与三角形法则一致吗?为什么?
向量加法的定义
(1) 两个法则的使用条件不同.
三角形法则适用于任意两个非零向量求和,平行四边形法则只适用于两个不共线的向量求和.
课文精讲
向量加法的平行四边形法则与三角形法则一致吗?为什么?
向量加法的定义
(2)当两个向量不共线时,两个法则是一致的.
如图所示, 在 ABCD中, ?????????= ?????????+ ?????????,
(平行四边形法则).
又因为????????= ????????,所以????????=
????????+ ????????(三角形法则).
?
????
?
????
?
????
?
????
?
课文精讲
向量加法的定义
思考:两个向量相加就是两个向量的模相加吗?
不是.因为向量既有大小,又有方向,
所以两个向量相加不是模相加,两个向量
相加应满足向量加法的三角形法则或平行
四边形法则.
课文精讲
若????,????共线,如图表示了两个共线向量求和的情形.
?
向量加法的定义
????
?
????
?
????
?
????
?
????+????
?
????
?
????
?
????+????
?
????
?
????
?
(1) (2)
课文精讲
若两个共线向量方向相同,则它们的和向量方向与原方向一致,大小为两个向量大小之和(如图(1));
向量加法的定义
????
?
????
?
????
?
????
?
????+????
?
(1)
课文精讲
若两个共线向量方向相反且大小不相等,则它们的和向量方向与较大向量的方向一致,大小是两个向量大小差的绝对值(如图(2)).
向量加法的定义
????
?
????
?
????+????
?
????
?
????
?
(2)
课文精讲
由向量加法的定义可知,互为相反向量的两个向量的和为零向量,即
?????+(- ????)=(- ????)+ ?????= ????.
?
向量加法的定义
典型例题
例1:如图,已知向量????,????,求作向量????+????.
?
解:作法1(平行四边形法则):如图在平面内任
取一点O,作????????= ????, ????????= ????,以OA,OB
为邻边作 OBCA,则????????=????+????.
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
典型例题
例1:如图,已知向量????,????,求作向量????+????.
?
解:作法2(三角形法则):如图在平面内任取一点O,作????????= ????, ????????= ????, ,则????????= ????+????.
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
课文精讲
思考
对任意的两个向量????,????,| ????+????|,|????|+|????|,
|????|-|????|之间具有怎样的大小关系?通过作图进行
解释.
?
向量加法的定义
||????|-|????||≤|????+????|≤|????|+|????|
?
????
?
????
?
????+?????
?
C
B
A
课文精讲
思考
对任意的两个向量????,????,| ????+????|,|????|+|????|,
|????|-|????|之间具有怎样的大小关系?通过作图进行
解释.
?
向量加法的定义
由上可看出,向量????,????的模与????+????的模之
间满足不等式
||????|-|????||≤|????+????|≤|????|+|????|
?
(向量形式的三角不等式)
课文精讲
点拨:利用向量形式的三角不等式可以解决有关向量的大小(模)的取值范围或最值问题,但需注意验证等号成立的条件,即当????与????同向时, |????+????|=|????|+|????| .
?
向量加法的定义
||????|-|????||≤|????+????|≤|????|+|????|
?
????
?
????
?
????+?????
?
C
B
A
典型例题
例2:轮船从A港沿北偏东60°方向行驶了40
n mile到达B处,再由B处沿正北方向行驶40
n mile到达C处.求此时轮船与A港的相对位置.
解:如图, ????????, ????????分别表示轮船的两次位移,
则 ????????表示轮船的合位移, ?????????= ?????????+ ????????.
设正东方向所在直线为AE,
过点B作AE的垂线,垂足为
点D.
?
典型例题
解:在Rt△ADB中,∠ADB=90°,
∠DAB=30°,|????????|=40 n mile,
所以 |????????|=|????????|·sin ∠DAB
=40·sin30°
=20(n mile).
?
例2:轮船从A港沿北偏东60°方向行驶了40
n mile到达B处,再由B处沿正北方向行驶40
n mile到达C处.求此时轮船与A港的相对位置.
典型例题
解:|????????|=|????????|·cos ∠DAB
=40·cos30°
=20????(n mile).
?
例2:轮船从A港沿北偏东60°方向行驶了40
n mile到达B处,再由B处沿正北方向行驶40
n mile到达C处.求此时轮船与A港的相对位置.
典型例题
解:在Rt△ADB中,∠ADC=90°, |????????|=|????????|+ |????????|=60 (n mile),由勾股定理得|????????|=|????????|????+|????????|????
= (????????????)????+????????????
= 40 ???? (n mile).
?
例2:轮船从A港沿北偏东60°方向行驶了40
n mile到达B处,再由B处沿正北方向行驶40
n mile到达C处.求此时轮船与A港的相对位置.
典型例题
解:由|????????|=2 |????????|,得∠CAD=60°.
因此,此时轮船位于A港北偏东30°,且
距A港40 ????的C处.
?
例2:轮船从A港沿北偏东60°方向行驶了40
n mile到达B处,再由B处沿正北方向行驶40
n mile到达C处.求此时轮船与A港的相对位置.
课文精讲
问题提出
我们熟知,数的加法满足结合律和交换
律,即对任意α,β,γ∈R,有
(α+β)+ γ= α+(β+γ)
α+β=β+α
那么向最的加法运算满足哪些运算律呢?
向量加法的运算律
课文精讲
分析理解
向量的加法也满足结合律和交换律,即
(????+????)+????=????+(????+????)
????+????=????+????
?
向量加法的运算律
结合律
交换律
课文精讲
分析理解
先证明向量????,????,????的加法满足结合律.
由图可知
(????+????)+????= (????????+????????)+????????= ????????+????????=????????,
????+ (????+????)= ????????+(????????+????????)= ????????+?????????= ????????.
所以 (????+????)+????=????+(????+????)
?
向量加法的运算律
结合律
????
?
????+????
?
????
?
????
?
????
?
????
?
????
?
????+????
?
????+????+????
?
????
?
课文精讲
分析理解
再证明向量????,????的加法满足交换律.由图
可知
????+????= ????????+????????= ????????,
????+????= ????????+????????=????????.
所以 ????+????=????+????
?
向量加法的运算律
交换律
????
?
????
?
????+????
?
????
?
????
?
????
?
????
?
????
?
????
?
课文精讲
多个向量的加法运算可按照任意的次序
与任意的组合进行,如
(????+????)+(????+????)=(????+????)+(????+????);
????+????+????+????+????=[????+(????+????)]+(????+????).
?
向量加法的运算律
典型例题
例3:如图,已知向量????,????,?????, ????,作出????+
????+?????+?????,并说明多个向量求和的方法及依据.
?
解:可以按照不同的次序与组合
进行这四个向量的加法.
????
?
????
?
????
?
????
?
典型例题
例3:如图,已知向量????,????,?????, ????,作出????+
????+?????+?????,并说明多个向量求和的方法及依据.
?
解:方法1
如图,在平面上任取一点A,
作????????=????,????????=????, ????????= ?????,
????????=????,
????+????+?????+?????=[(????+????)+ ????]+ ?????
=(????????+????)+ ?????= ????????+ ?????= ????????.
?
????
?
????
?
????
?
????
?
????
?
????+????+?????+????
?
????
?
????
?
????
?
A
C
B
D
E
典型例题
例3:如图,已知向量????,????,?????, ????,作出????+
????+?????+?????,并说明多个向量求和的方法及依据.
?
解:方法2
如图,在平面上任取一点A′,
作????′????′=????,????′????′=????, ????′????′= ?????, ????′????′=????,则
????+????+?????+?????=(????+????)+( ????+ ????)
=????′????′+????′????′= ????′????′.
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????+????+?????+?????
?
A′
C′
B′
D′
E′
课文精讲
由于向量的加法满足结合律与交换律,
因此求n个向量????????, ????????, ···, ????????,的和可
以按以下步骤进行:
任取一点O,依次作有向线段?????????????=????????,
?????????????????=????????, ···, ??????????????????????= ????????, ????????????即为
这n个向量之和.
?
当然,也可以把n个向量分为若干组,
先求每组向量之和,再求出这些组向量和的
和.
课文精讲
另外,为了得到有限个向量的和,只需将
这些向量依次首尾相接,那么以第一个向量的
始点为始点,最后一个向量的终点为终点的向
量,就是这些向量的和,如图所示.
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????+????+????+????+????
?
课文精讲
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????
?
????+????+????+????+????
?
图中的和,与向量相加的顺序有关吗?为
什么?
无关,因为向量相加满足交换律
综合练习
化简下列各式:
(1)????????+????????+????????; (2)????????+????????+????????+????????+????????.
?
解:(1)????????+????????+????????
=(????????+????????)+????????
=????????+????????
=????????.
?
综合练习
化简下列各式:
(1)????????+????????+????????; (2)????????+????????+????????+????????+????????.
?
解: (2)????????+????????+????????+????????+????????
=????????+????????+(????????+????????+????????)
=????????+????????+????????
=(????????+????????)+????????
=????????+????????
=????????=????.
?
综合练习
已知|????|=3, |????|=4,求|????+????|的最大值和最小值,并说明取得最大值和最小值时 ????与????的关系.
?
解:由|????+????|≤|????|+|????|
可知, |????+????|的最大值为|????|+|????| =3+4=7.
当且仅当????与????方向相同时取得最大值.
由|????+????| ≥||????|-|????||,可知|????+????|的最小值为||????|-|????||=|3-4|=1.
当且仅当与方向相反时取得最小值.
?
本课小结
再 见
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
