2.2.2向量的减法-【新教材】2020-2021学年北师大版(2019)高中数学必修第二册课件(19张PPT)
文档属性
| 名称 | 2.2.2向量的减法-【新教材】2020-2021学年北师大版(2019)高中数学必修第二册课件(19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 773.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 00:00:00 | ||
图片预览




文档简介
向量的减法
授课教师:
温故知新
学习目标
1.理解相反向量的含义,能用相反向量说出向量
相减的意义;(重点)
2.掌握向量减法的运算及其几何意义,能熟练地
进行向量的加减运算;(难点)
3.能将向量的减法运算转化为向量的加法运算.(难点)
课文精讲
我们知道,实数α减去实数β,等于实数α
加上实数β的相反数,即
α- β= α+(- β).
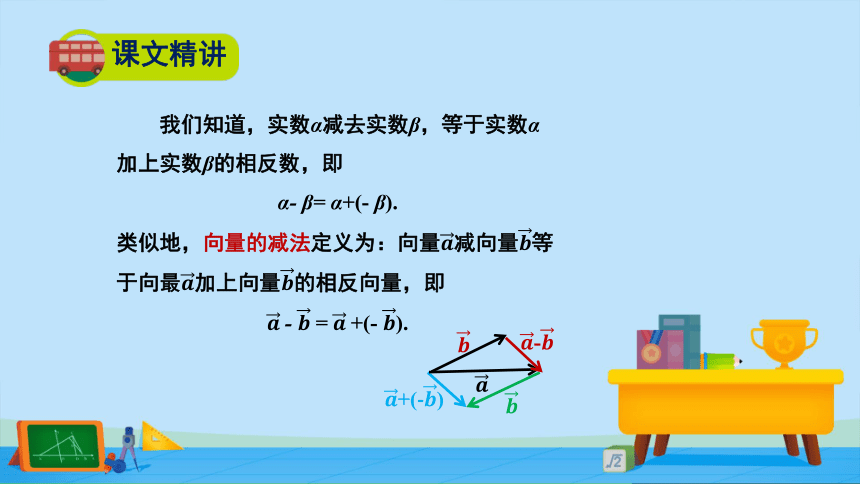
类似地,向量的减法定义为:向量????减向量????等
于向最????加上向量????的相反向量,即
?????- ?????= ?????+(- ????).
?
????
?
????
?
????
?
????-?????
?
????+(-????)
?
课文精讲
不难看出,任何一个向量与它的相反向量
的和等于零向量,即
????+(- ????)= ???? ,????????+(- ????????)= ????.
?
思考:怎样正确理解相反向量?
相反向量与相等向量一样,要从长度和
方向两方面去理解,相反向量必为平行向量.
课文精讲
相反向量的性质:
(1)-(- ????)= ????;
(2) ????+(- ????)=- ????+ ????= ????;
(3)若????与????互为相反向量,则
① ????=- ????, ????=- ????;
② ????+ ????= ????;
③|????|=|????|.
?
课文精讲
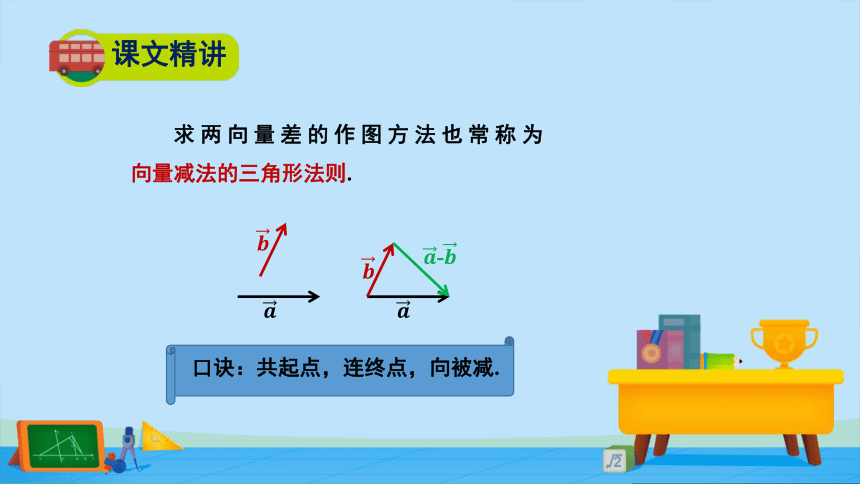
口诀:共起点,连终点,向被减.
????
?
????
?
????
?
????
?
????-?????
?
求两向量差的作图方法也常称为
向量减法的三角形法则.
课文精讲
????
?
????
?
????
?
????
?
????-?????
?
向量????-????可以表示为从向量????的终点指
向向量????的终点的向量,这是向量减法的几
何意义.
?
课文精讲
如图,给定向量????减向量????,作有向线段????????= ????, ????????= ????,故-????=????????,则
?????- ?????= ?????+(- ????)=????????+ ????????= ????????+ ????????= ????????.
?
????
?
????
?
????
?
????
?
-????
?
????
?
课文精讲
思考:向量的减法满足交换律和结合律吗?
不满足交换律,但满足结合律,即
① ?????- ?????≠ ????-????;
②(?????- ?????)- ????= ????-(?????+ ?????).
?
典型例题
例1:如图①,已知向量????,????,????,求作向量
????-????+ ????.
?
解:如图②,在平面上任取一点O,作????????= ????,????????= ????, 则????????= ????- ????.
再作????????= ????,连接BD,
则????????= ????????+ ????????=????-????+ ????.
?
????
?
????
?
????
?
①
????
?
????
?
????
?
????-????
?
②
B
D
A
O
典型例题
例2:已知|????|=6,| ????|=8,且????⊥????.
(1)探索|????+????|与|????-????|的关系;
(2)求|????- ????|.
?
解:如图,设????????= ????,????????= ????,以AB,AD为邻边作 ABCD,则????????= ????+????,????????= ????-????.
?
(1)因为????⊥????,即????????⊥????????,
所以 ABCD为矩形,
所以|????????|=|????????|,
即|????+????|=|????-????|.
?
????
?
D
A
B
C
????
?
典型例题
例2:已知|????|=6,| ????|=8,且????⊥????.
(1)探索|????+????|与|????-????|的关系;
(2)求|????- ????|.
?
解:
(2)在Rt△DAB中,|????????|=6,|????????|=8,
由勾股定理,得
|????????|2= |????????|2+|????????|2=62+82=100.
所以|????- ????|=|????????|=10.
?
????
?
D
A
B
C
????
?
典型例题
例3:如图,点O是 ABCD外一点,试用
????????, ????????, ????????表示????????.
?
解:由于????????= ????????+ ????????,
因此只需将????????用????????, ????????表示.
而????????=???????? = ?????????-?????????,
故????????= ????????+ ????????=????????+(?????????-?????????)
= ?????????-?????????+????????.
?
D
A
B
C
O
错误使用向量的减法法则
如图,已知一点O到平行四边形ABCD的三个顶点A,B,C的向量分别为????????,???????? ,????????,求????????.
?
解:因为????????=????????+????????,
????????=????????=????????-????????,
所以????????=????????+????????-????????= ????????+ ????????- ????????.
?
A
B
C
D
O
????????
?
????????
?
????????
?
综合练习
综合练习
错误使用向量的减法法则
注意:
可以表示为从向量????的终点指向????
的终点的向量,这是向量减法的几何意义.
连终点,向被减.
?
????-????
?
综合练习
已知平行四边形ABCD中, ????????=?????, ????????=?????,用????,????分别表示向量????????, ????????.
?
解:如图所示,由向量加法的平行四边形法则
可知????????=????????+ ????????= ????+????.
按照减法的定义可知
????????=????????- ????????= ????-????.
?
????
?
????
?
A
B
C
D
本课小结
再 见
授课教师:
温故知新
学习目标
1.理解相反向量的含义,能用相反向量说出向量
相减的意义;(重点)
2.掌握向量减法的运算及其几何意义,能熟练地
进行向量的加减运算;(难点)
3.能将向量的减法运算转化为向量的加法运算.(难点)
课文精讲
我们知道,实数α减去实数β,等于实数α
加上实数β的相反数,即
α- β= α+(- β).
类似地,向量的减法定义为:向量????减向量????等
于向最????加上向量????的相反向量,即
?????- ?????= ?????+(- ????).
?
????
?
????
?
????
?
????-?????
?
????+(-????)
?
课文精讲
不难看出,任何一个向量与它的相反向量
的和等于零向量,即
????+(- ????)= ???? ,????????+(- ????????)= ????.
?
思考:怎样正确理解相反向量?
相反向量与相等向量一样,要从长度和
方向两方面去理解,相反向量必为平行向量.
课文精讲
相反向量的性质:
(1)-(- ????)= ????;
(2) ????+(- ????)=- ????+ ????= ????;
(3)若????与????互为相反向量,则
① ????=- ????, ????=- ????;
② ????+ ????= ????;
③|????|=|????|.
?
课文精讲
口诀:共起点,连终点,向被减.
????
?
????
?
????
?
????
?
????-?????
?
求两向量差的作图方法也常称为
向量减法的三角形法则.
课文精讲
????
?
????
?
????
?
????
?
????-?????
?
向量????-????可以表示为从向量????的终点指
向向量????的终点的向量,这是向量减法的几
何意义.
?
课文精讲
如图,给定向量????减向量????,作有向线段????????= ????, ????????= ????,故-????=????????,则
?????- ?????= ?????+(- ????)=????????+ ????????= ????????+ ????????= ????????.
?
????
?
????
?
????
?
????
?
-????
?
????
?
课文精讲
思考:向量的减法满足交换律和结合律吗?
不满足交换律,但满足结合律,即
① ?????- ?????≠ ????-????;
②(?????- ?????)- ????= ????-(?????+ ?????).
?
典型例题
例1:如图①,已知向量????,????,????,求作向量
????-????+ ????.
?
解:如图②,在平面上任取一点O,作????????= ????,????????= ????, 则????????= ????- ????.
再作????????= ????,连接BD,
则????????= ????????+ ????????=????-????+ ????.
?
????
?
????
?
????
?
①
????
?
????
?
????
?
????-????
?
②
B
D
A
O
典型例题
例2:已知|????|=6,| ????|=8,且????⊥????.
(1)探索|????+????|与|????-????|的关系;
(2)求|????- ????|.
?
解:如图,设????????= ????,????????= ????,以AB,AD为邻边作 ABCD,则????????= ????+????,????????= ????-????.
?
(1)因为????⊥????,即????????⊥????????,
所以 ABCD为矩形,
所以|????????|=|????????|,
即|????+????|=|????-????|.
?
????
?
D
A
B
C
????
?
典型例题
例2:已知|????|=6,| ????|=8,且????⊥????.
(1)探索|????+????|与|????-????|的关系;
(2)求|????- ????|.
?
解:
(2)在Rt△DAB中,|????????|=6,|????????|=8,
由勾股定理,得
|????????|2= |????????|2+|????????|2=62+82=100.
所以|????- ????|=|????????|=10.
?
????
?
D
A
B
C
????
?
典型例题
例3:如图,点O是 ABCD外一点,试用
????????, ????????, ????????表示????????.
?
解:由于????????= ????????+ ????????,
因此只需将????????用????????, ????????表示.
而????????=???????? = ?????????-?????????,
故????????= ????????+ ????????=????????+(?????????-?????????)
= ?????????-?????????+????????.
?
D
A
B
C
O
错误使用向量的减法法则
如图,已知一点O到平行四边形ABCD的三个顶点A,B,C的向量分别为????????,???????? ,????????,求????????.
?
解:因为????????=????????+????????,
????????=????????=????????-????????,
所以????????=????????+????????-????????= ????????+ ????????- ????????.
?
A
B
C
D
O
????????
?
????????
?
????????
?
综合练习
综合练习
错误使用向量的减法法则
注意:
可以表示为从向量????的终点指向????
的终点的向量,这是向量减法的几何意义.
连终点,向被减.
?
????-????
?
综合练习
已知平行四边形ABCD中, ????????=?????, ????????=?????,用????,????分别表示向量????????, ????????.
?
解:如图所示,由向量加法的平行四边形法则
可知????????=????????+ ????????= ????+????.
按照减法的定义可知
????????=????????- ????????= ????-????.
?
????
?
????
?
A
B
C
D
本课小结
再 见
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
