5.3.2 线段垂直平分线的性质及画法(知识清单+经典例题+夯实基础+提优特训+中考链接)
文档属性
| 名称 | 5.3.2 线段垂直平分线的性质及画法(知识清单+经典例题+夯实基础+提优特训+中考链接) |  | |
| 格式 | zip | ||
| 文件大小 | 445.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-08 22:28:32 | ||
图片预览



文档简介
21世纪教育网
–全国领先的中小学教育资源及组卷应用平台
北师大版2020﹣2021学年度下学期七年级数学下册第五章生活中的轴对称
5.3
简单的轴对称图形
第二课时
线段垂直平分线的性质和画法
【知识清单】
1.线段的垂直平分线:垂直于一条线段,并且平分这条线段的直线,叫做这条线段的垂直平分线(简称中垂线);线段是轴对称图形,垂直并且平分线段的直线是它的一条对称轴.
2.
线段的垂直平分线的性质:
线段垂直平分线上的点到这条线段两个端点的距离相等.
3.如图,已知线段AB.用尺规作出线段AB的垂直平分线l.
作法:(1)分别以点A,B为圆心,大于线段AB长度的为半径画圆弧,
两弧相交于点C,D;
(2)过点C,D作直线CD.
直线CD就是线段AB的垂直平分线.
【经典例题】
例题1、如图,直线l是线段AB的垂直平分线,垂足为点D,点P是l上任意一点,则下列结论:①PA=PB;②l⊥AB;③S△PAD=S△PBD;④∠APD=∠BPD;⑤PD=BD中,正确的有( )
A.①②③
B.①②⑤
C.①②③④
D.①②③④⑤
【考点】等腰三角形的性质;三角形内角和定理.
【分析】从已知条开始件结合线段的垂直平分线的性质
进行思得到结论与各选项进行比对,可得到答案考.
【解答】解:①l是AB的垂直平分线,故PA=PB,正确;
②根据垂直平分线的定义,l⊥AB,正确;
③根据轴对称图形的性质,△PAD≌△PBD,所以S△PAD=S△PBD,正确;
④根据轴对称图形的性质,△PAD≌△PBD,所以∠APD=∠BPD,正确;
⑤由线段AB的垂直平分线的性质,不能保证PD=BD,错误.
故选C
【点评】此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.线段的垂直平分线垂直于这条线段并且平分这条线段.
例题2、已知:如图,在△ABC中,
AB的垂直平分线DE分别交BC,AB于点E,D,且CE=3BE.求证:CE=3AE.
【考点】线段垂直平分线的性质.?
【分析】要证CE=3AE,CE与AE没有直接关系,而已知DE是线段AB的垂直平分线,可连接AE.由线段垂直平分线性质定理得出AE=BE,由此得出结论.
【解答】连接AE.
∵DE是AB的垂直平分线,
∴BE=AE,
∵CE=3BE.
∴CE=3AE.
【点评】此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段
的两个端点的距离相等.
【夯实基础】
1.已知点P到△ABC的三个顶点的距离,则点P一定是(
)
A.三条中线的交点
B.三条角平分线的交点
C.三条高线的交点
D.三边的垂直平分线的交点
2.如图,已知△ABC,AB乙、丙、丁四位同学的作法如下:请你判断哪位同学的作法正确(
)
A.甲
B.乙
C.丙
D.丁
3.如图,MN是线段AB的垂直平分线,C在MN外,且与A点在MN的同一侧,BC交MN
于P点,则( )
A.BC>PC+AP
B.BCC.BC≥PC+AP
D.BC=PC+AP
4.如图,在等腰△ABC中,AB=AC,∠A=40°,边AB的垂直平分线交AB于E,交AC于D,
连接BD,则∠CBD=
(
)
A.40°
B.30°
C.20°
D.10°
5.三边的垂直平分线的交点在其内部,则这个三角形是
;三边的垂直平分线的交点在三角形一边上,则这个三角形是
;三边的垂直平分线的交点在三角形外部,则这个三角形是
.
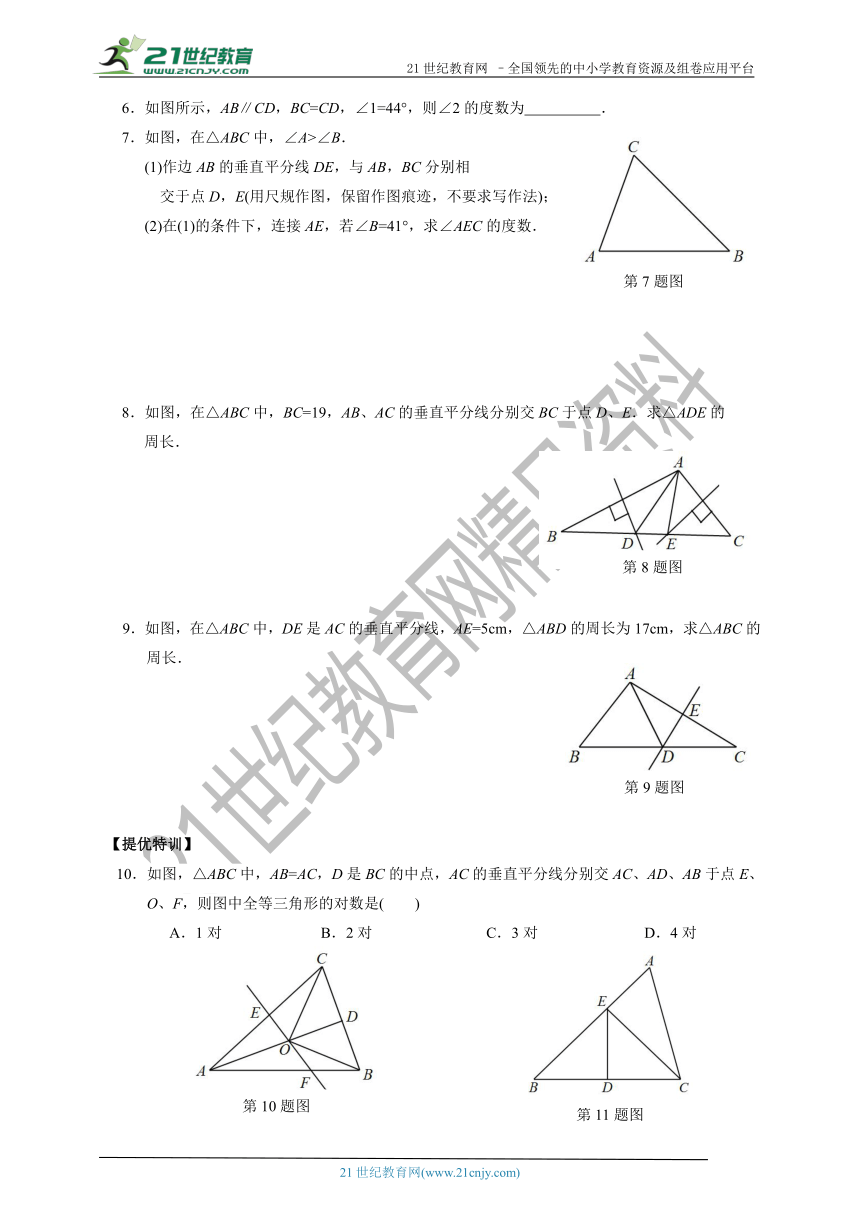
6.如图所示,AB∥CD,BC=CD,∠1=44°,则∠2的度数为
.
7.如图,在△ABC中,∠A>∠B.
(1)作边AB的垂直平分线DE,与AB,BC分别相
交于点D,E(用尺规作图,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,连接AE,若∠B=41°,求∠AEC的度数.
8.如图,在△ABC中,BC=19,AB、AC的垂直平分线分别交BC于点D、E.求△ADE的
周长.
9.如图,在△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为17cm,求△ABC的周长.
【提优特训】
10.如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )
A.1对
B.2对
C.3对
D.4对
11.如图,在△ABC中,DE是BC的垂直平分线,垂足为点D,交AB于点E,已知BE=5,AE=3,若AC的长为奇数,则下列选项正确是(
)
A.3或5
B.5或7
C.5或7或9
D.3或5或7
12.如图,在△ABC中,DE是BC的垂直平分线,垂足为点D,交AB于点E,若AB+AC=19,△AEC的周长为(
)
A.9
B.19
C.38
D.无法确定
13.如图,在△ABC中,∠C
=90°,边AB的垂直平分线交BC于点D,交AB于E,若AD是∠CAB的平分线,则∠B
=(
)
A.20°
B.25°
C.30°
D.40°
14.如图,在△ABC中,AB=AC,∠A
=120°,BC=15cm,AB的垂直平分线交BC于点D,交AB于E,AC的垂直平分线交BC于点M,交AC于点N,则DM的长为
.
15.如图,点D是线段AB与线段BC的垂直平分线的交点,∠BAC=28°,则图中有
个等腰三角形,∠BDC
=
度.
16.如图,等边△ABC的边长为4cm,D,E分别是AB、AC上的点,将△ADE沿直线DE折叠,
点A落在点F处,且点F在△ABC外部,则阴影部分图形的周长为
cm.
17.在△ABC中,∠BAC=∠BCA,BC的垂直平分线DE交AC所在直线于点E,交BC于点D.
(1)如图(1),若∠B=60°,BC的垂直平分线DE中的E恰与点A重合,求∠CED的度数;
(2)如图(2),若∠B=84°,BC的垂直平分线DE交线段AC于点E,求∠CED的度数;
(3)如图(3),若∠B=44°,BC的垂直平分线DE交CA的延长线于点E,求∠CED的度数;
(4)若∠B=α,无论BC的垂直平分线DE与AC的交点在哪,求∠CED的度数.
18.如图,要在公路MN旁修建一个货物中转站P,分别向A、B两个开发区运货.
(1)若要求货站到A、B两个开发区的距离相等,那么货站应建在那里?
(2)若要求货站到A、B两个开发区的距离和最小,那么货站应建在那里?
(分别在图上找出点P,并保留作图痕迹,写出相应的文字说明.)
【中考链接】
19.(2020年?山东枣庄)
如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,
连接AE.若BC=6,AC=5,则△ACE的周长为(
)
A.8
B.11
C.16
D.17
20.(2020年?湖南益阳)
如图,在△ABC中,AC的垂直平分线交AB于点D,DC平分∠ACB,若∠A=50°,则∠B的度数为(
)
A.25°
B.30°
C.35°
D.40°
参考答案
1、D
2、C
3、D
4、B
5、锐角三角形,直角三角形,钝角三角形
6、68°
10、D
11、D
12、B
13、C
14、5cm
15、56
16、12
19、B
20、B
7.如图,在△ABC中,∠A>∠B.
(1)作边AB的垂直平分线DE,与AB,BC分别相
交于点D,E(用尺规作图,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,连接AE,若∠B=41°,求∠AEC的度数.
解:(1)画图,如图所示;
(2)∵DE是AB的垂直平分线,
∴AE=BE,
∴∠EAB=∠B=41°,
∴∠AEC=∠EAB+∠B=82°.
8.如图,在△ABC中,BC=19,AB、AC的垂直平分线分别交BC于点D、E.求△ADE的
周长.
解:∵AB、AC的垂直平分线分别交BC于D、E,
∴AD=BD,AE=CE,
∴△ADE的周长=AD+DE+AE=BD+DE+CE=BC=19.
9.如图,在△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为17cm,求△ABC的周长.
解:∵DE垂直平分线段AC,
∴AD=CD,AC=2AE,
∴△ABD的周长=AB+BD+AD=AB+BD+DC=AB+BC,
∵AE=5cm,△ABD的周长为17cm,
∴△ABC的周长=AB+AC+BC=2×5+17=10+17=27cm.
17.在△ABC中,∠BAC=∠BCA,BC的垂直平分线DE交AC所在直线于点E,交BC于点D.
(1)如图(1),若∠B=60°,BC的垂直平分线DE中的E恰与点A重合,求∠CED的度数;
(2)如图(2),若∠B=84°,BC的垂直平分线DE交线段AC于点E,求∠CED的度数;
(3)如图(3),若∠B=44°,BC的垂直平分线DE交CA的延长线于点E,求∠CED的度数;
(4)若∠B=α,无论BC的垂直平分线DE与AC的交点在哪,求∠CED的度数.
解:(1)∵∠BAC=∠BCA,∠B=60°,
∴∠C=(180°?∠B)=(180°?60°)=60°,
∵DE是BC的垂直平分线,
∴DE⊥BC,
∴∠CED=90°?∠C=90°?60°=30°;
(2)∵∠BAC=∠BCA,∠B=84°,
∴∠C=(180°?∠B)=(180°?84°)=48°,
∵DE是BC的垂直平分线,
∴DE⊥BC,
∴∠CED=90°?∠C=90°?48°=42°;
(3)∵∠BAC=∠BCA,∠B=44°,
∴∠C=(180°?∠B)=(180°?44°)=68°,
∵DE是BC的垂直平分线,
∴DE⊥BC,
∴∠CED=90°?∠C=90°?68°=22°;
(4)∵∠BAC=∠BCA,∠B=α,
∴∠C=(180°?∠B)=(180°?α),
∵DE是BC的垂直平分线,
∴DE⊥BC,
∴∠CED=90°?∠C=90°?(180°?α)=α.
18.如图,要在公路MN旁修建一个货物中转站P,分别向A、B两个开发区运货.
(1)若要求货站到A、B两个开发区的距离相等,那么货站应建在那里?
(2)若要求货站到A、B两个开发区的距离和最小,那么货站应建在那里?
(分别在图上找出点P,并保留作图痕迹,写出相应的文字说明.)
解:如图(1)①连接AB,
②作线段AB的垂直平分线,交DE于点P,
点P就是所求的点;
如图(2)①作点A关于直线DE的对称点,
②连接B,交DE于点P,
点P就是所求的点.
第14题图
第19题图
第15题图
第18题图(1)
第18题图(2)
第3题图
第12题图
第8题图
第7题图
第20题图
第13题图
第6题图
第11题图
第10题图
第17题(1)
第17题(2)
第17题(3)
甲
乙
丙
丁
第16题图
第4题图
第18题图(2)
第18题图(1)
第18题图(1)
第18题图(2)
第17题(1)
第17题(2)
第17题(3)
第9题图
第8题图
第9题图
第7题图
例题1图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
–全国领先的中小学教育资源及组卷应用平台
北师大版2020﹣2021学年度下学期七年级数学下册第五章生活中的轴对称
5.3
简单的轴对称图形
第二课时
线段垂直平分线的性质和画法
【知识清单】
1.线段的垂直平分线:垂直于一条线段,并且平分这条线段的直线,叫做这条线段的垂直平分线(简称中垂线);线段是轴对称图形,垂直并且平分线段的直线是它的一条对称轴.
2.
线段的垂直平分线的性质:
线段垂直平分线上的点到这条线段两个端点的距离相等.
3.如图,已知线段AB.用尺规作出线段AB的垂直平分线l.
作法:(1)分别以点A,B为圆心,大于线段AB长度的为半径画圆弧,
两弧相交于点C,D;
(2)过点C,D作直线CD.
直线CD就是线段AB的垂直平分线.
【经典例题】
例题1、如图,直线l是线段AB的垂直平分线,垂足为点D,点P是l上任意一点,则下列结论:①PA=PB;②l⊥AB;③S△PAD=S△PBD;④∠APD=∠BPD;⑤PD=BD中,正确的有( )
A.①②③
B.①②⑤
C.①②③④
D.①②③④⑤
【考点】等腰三角形的性质;三角形内角和定理.
【分析】从已知条开始件结合线段的垂直平分线的性质
进行思得到结论与各选项进行比对,可得到答案考.
【解答】解:①l是AB的垂直平分线,故PA=PB,正确;
②根据垂直平分线的定义,l⊥AB,正确;
③根据轴对称图形的性质,△PAD≌△PBD,所以S△PAD=S△PBD,正确;
④根据轴对称图形的性质,△PAD≌△PBD,所以∠APD=∠BPD,正确;
⑤由线段AB的垂直平分线的性质,不能保证PD=BD,错误.
故选C
【点评】此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段的两个端点的距离相等.线段的垂直平分线垂直于这条线段并且平分这条线段.
例题2、已知:如图,在△ABC中,
AB的垂直平分线DE分别交BC,AB于点E,D,且CE=3BE.求证:CE=3AE.
【考点】线段垂直平分线的性质.?
【分析】要证CE=3AE,CE与AE没有直接关系,而已知DE是线段AB的垂直平分线,可连接AE.由线段垂直平分线性质定理得出AE=BE,由此得出结论.
【解答】连接AE.
∵DE是AB的垂直平分线,
∴BE=AE,
∵CE=3BE.
∴CE=3AE.
【点评】此题主要考查线段的垂直平分线的性质等几何知识.线段的垂直平分线上的点到线段
的两个端点的距离相等.
【夯实基础】
1.已知点P到△ABC的三个顶点的距离,则点P一定是(
)
A.三条中线的交点
B.三条角平分线的交点
C.三条高线的交点
D.三边的垂直平分线的交点
2.如图,已知△ABC,AB
)
A.甲
B.乙
C.丙
D.丁
3.如图,MN是线段AB的垂直平分线,C在MN外,且与A点在MN的同一侧,BC交MN
于P点,则( )
A.BC>PC+AP
B.BC
D.BC=PC+AP
4.如图,在等腰△ABC中,AB=AC,∠A=40°,边AB的垂直平分线交AB于E,交AC于D,
连接BD,则∠CBD=
(
)
A.40°
B.30°
C.20°
D.10°
5.三边的垂直平分线的交点在其内部,则这个三角形是
;三边的垂直平分线的交点在三角形一边上,则这个三角形是
;三边的垂直平分线的交点在三角形外部,则这个三角形是
.
6.如图所示,AB∥CD,BC=CD,∠1=44°,则∠2的度数为
.
7.如图,在△ABC中,∠A>∠B.
(1)作边AB的垂直平分线DE,与AB,BC分别相
交于点D,E(用尺规作图,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,连接AE,若∠B=41°,求∠AEC的度数.
8.如图,在△ABC中,BC=19,AB、AC的垂直平分线分别交BC于点D、E.求△ADE的
周长.
9.如图,在△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为17cm,求△ABC的周长.
【提优特训】
10.如图,△ABC中,AB=AC,D是BC的中点,AC的垂直平分线分别交AC、AD、AB于点E、O、F,则图中全等三角形的对数是( )
A.1对
B.2对
C.3对
D.4对
11.如图,在△ABC中,DE是BC的垂直平分线,垂足为点D,交AB于点E,已知BE=5,AE=3,若AC的长为奇数,则下列选项正确是(
)
A.3或5
B.5或7
C.5或7或9
D.3或5或7
12.如图,在△ABC中,DE是BC的垂直平分线,垂足为点D,交AB于点E,若AB+AC=19,△AEC的周长为(
)
A.9
B.19
C.38
D.无法确定
13.如图,在△ABC中,∠C
=90°,边AB的垂直平分线交BC于点D,交AB于E,若AD是∠CAB的平分线,则∠B
=(
)
A.20°
B.25°
C.30°
D.40°
14.如图,在△ABC中,AB=AC,∠A
=120°,BC=15cm,AB的垂直平分线交BC于点D,交AB于E,AC的垂直平分线交BC于点M,交AC于点N,则DM的长为
.
15.如图,点D是线段AB与线段BC的垂直平分线的交点,∠BAC=28°,则图中有
个等腰三角形,∠BDC
=
度.
16.如图,等边△ABC的边长为4cm,D,E分别是AB、AC上的点,将△ADE沿直线DE折叠,
点A落在点F处,且点F在△ABC外部,则阴影部分图形的周长为
cm.
17.在△ABC中,∠BAC=∠BCA,BC的垂直平分线DE交AC所在直线于点E,交BC于点D.
(1)如图(1),若∠B=60°,BC的垂直平分线DE中的E恰与点A重合,求∠CED的度数;
(2)如图(2),若∠B=84°,BC的垂直平分线DE交线段AC于点E,求∠CED的度数;
(3)如图(3),若∠B=44°,BC的垂直平分线DE交CA的延长线于点E,求∠CED的度数;
(4)若∠B=α,无论BC的垂直平分线DE与AC的交点在哪,求∠CED的度数.
18.如图,要在公路MN旁修建一个货物中转站P,分别向A、B两个开发区运货.
(1)若要求货站到A、B两个开发区的距离相等,那么货站应建在那里?
(2)若要求货站到A、B两个开发区的距离和最小,那么货站应建在那里?
(分别在图上找出点P,并保留作图痕迹,写出相应的文字说明.)
【中考链接】
19.(2020年?山东枣庄)
如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,
连接AE.若BC=6,AC=5,则△ACE的周长为(
)
A.8
B.11
C.16
D.17
20.(2020年?湖南益阳)
如图,在△ABC中,AC的垂直平分线交AB于点D,DC平分∠ACB,若∠A=50°,则∠B的度数为(
)
A.25°
B.30°
C.35°
D.40°
参考答案
1、D
2、C
3、D
4、B
5、锐角三角形,直角三角形,钝角三角形
6、68°
10、D
11、D
12、B
13、C
14、5cm
15、56
16、12
19、B
20、B
7.如图,在△ABC中,∠A>∠B.
(1)作边AB的垂直平分线DE,与AB,BC分别相
交于点D,E(用尺规作图,保留作图痕迹,不要求写作法);
(2)在(1)的条件下,连接AE,若∠B=41°,求∠AEC的度数.
解:(1)画图,如图所示;
(2)∵DE是AB的垂直平分线,
∴AE=BE,
∴∠EAB=∠B=41°,
∴∠AEC=∠EAB+∠B=82°.
8.如图,在△ABC中,BC=19,AB、AC的垂直平分线分别交BC于点D、E.求△ADE的
周长.
解:∵AB、AC的垂直平分线分别交BC于D、E,
∴AD=BD,AE=CE,
∴△ADE的周长=AD+DE+AE=BD+DE+CE=BC=19.
9.如图,在△ABC中,DE是AC的垂直平分线,AE=5cm,△ABD的周长为17cm,求△ABC的周长.
解:∵DE垂直平分线段AC,
∴AD=CD,AC=2AE,
∴△ABD的周长=AB+BD+AD=AB+BD+DC=AB+BC,
∵AE=5cm,△ABD的周长为17cm,
∴△ABC的周长=AB+AC+BC=2×5+17=10+17=27cm.
17.在△ABC中,∠BAC=∠BCA,BC的垂直平分线DE交AC所在直线于点E,交BC于点D.
(1)如图(1),若∠B=60°,BC的垂直平分线DE中的E恰与点A重合,求∠CED的度数;
(2)如图(2),若∠B=84°,BC的垂直平分线DE交线段AC于点E,求∠CED的度数;
(3)如图(3),若∠B=44°,BC的垂直平分线DE交CA的延长线于点E,求∠CED的度数;
(4)若∠B=α,无论BC的垂直平分线DE与AC的交点在哪,求∠CED的度数.
解:(1)∵∠BAC=∠BCA,∠B=60°,
∴∠C=(180°?∠B)=(180°?60°)=60°,
∵DE是BC的垂直平分线,
∴DE⊥BC,
∴∠CED=90°?∠C=90°?60°=30°;
(2)∵∠BAC=∠BCA,∠B=84°,
∴∠C=(180°?∠B)=(180°?84°)=48°,
∵DE是BC的垂直平分线,
∴DE⊥BC,
∴∠CED=90°?∠C=90°?48°=42°;
(3)∵∠BAC=∠BCA,∠B=44°,
∴∠C=(180°?∠B)=(180°?44°)=68°,
∵DE是BC的垂直平分线,
∴DE⊥BC,
∴∠CED=90°?∠C=90°?68°=22°;
(4)∵∠BAC=∠BCA,∠B=α,
∴∠C=(180°?∠B)=(180°?α),
∵DE是BC的垂直平分线,
∴DE⊥BC,
∴∠CED=90°?∠C=90°?(180°?α)=α.
18.如图,要在公路MN旁修建一个货物中转站P,分别向A、B两个开发区运货.
(1)若要求货站到A、B两个开发区的距离相等,那么货站应建在那里?
(2)若要求货站到A、B两个开发区的距离和最小,那么货站应建在那里?
(分别在图上找出点P,并保留作图痕迹,写出相应的文字说明.)
解:如图(1)①连接AB,
②作线段AB的垂直平分线,交DE于点P,
点P就是所求的点;
如图(2)①作点A关于直线DE的对称点,
②连接B,交DE于点P,
点P就是所求的点.
第14题图
第19题图
第15题图
第18题图(1)
第18题图(2)
第3题图
第12题图
第8题图
第7题图
第20题图
第13题图
第6题图
第11题图
第10题图
第17题(1)
第17题(2)
第17题(3)
甲
乙
丙
丁
第16题图
第4题图
第18题图(2)
第18题图(1)
第18题图(1)
第18题图(2)
第17题(1)
第17题(2)
第17题(3)
第9题图
第8题图
第9题图
第7题图
例题1图
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
