三年级上册数学教案-集合 人教版
图片预览


文档简介
数学广角——集合
教学目标:
1.
通过观察、猜测、操作、交流等活动,让学生在自主探究活动中感知集合图形成的过程,体会集合图的优点。
2.
能借助直观图,用集合图分析并解决生活中简单的有重复部分的问题。
3.
渗透多种方法解决重叠问题的意识,培养学生善于观察、勤于思考的学习习惯。
教学重点:
理解集合图各部分的意义,能用集合图分析生活中简单的有重复部分的问题。
教学难点:
使学生会借助直观图,利用集合的思想方法解决简单的实际问题。
教学过程:
游戏导入
“脑筋急转弯”游戏:房间里有两个爸爸,两个儿子,但是只有三个人,这是怎么回事?(强调爸爸身份的双重性——身份重复了)
预设:这三个人是儿子、爸爸、爷爷。
设计意图:通过学生喜爱的脑筋急转弯引入,激发了学生无限的学习兴趣,同时引导学生大胆的猜想,让学生在猜测中学会思考,在争论中学会倾听、学会交流、学会整合。
探究新知
课件出示三(1)班参加跳绳、踢毽比赛的学生名单。
提出问题:有几个人参加跳绳比赛?有几个人参加踢毽比赛?
预设:参加跳绳的有9人,参加踢毽子的有8人。
提出问题:观察表格内容,你有什么发现呢?
预设:有些人的名字是重复的。
提出问题:哪些人?有没有什么办法,能清楚地看出有三人重复呢?
提出要求:把重复的人名圈出来,用表格整理出来。
跳绳
杨明
刘红
李芳
陈东
王爱华
马超
丁旭
赵军
徐强
踢毽
于丽
周晓
朱晓东
陶伟
卢强
?
教师说明:同学们现在表格人数比较少容易找人名,但是表格人多时就不好找了。那我们今天就来用集合的方法来解决这一问题。
提出要求:老师把两个圈都贴在黑板上了,请两位同学来帮老师把两组参赛的同学人名分别贴在黑板上两个圈里面。
两个学生操作!
预设:
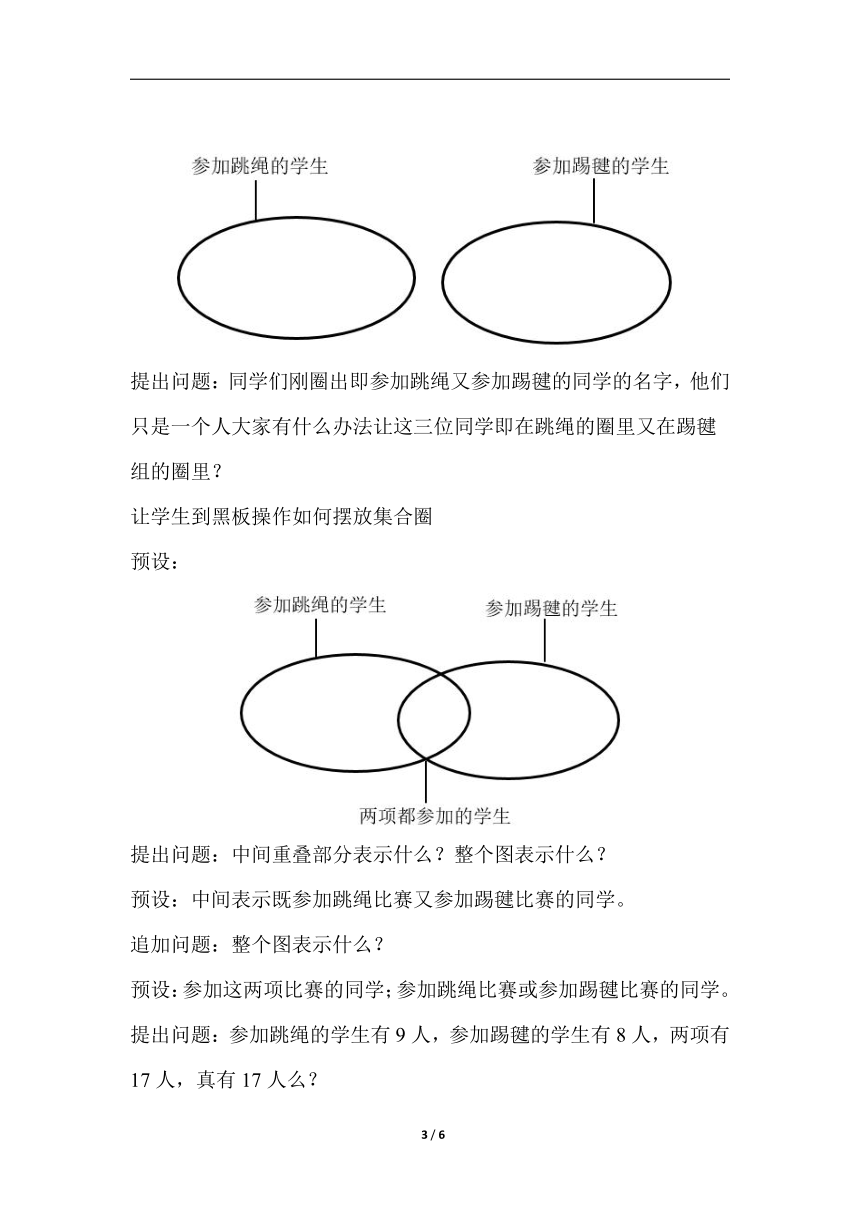
提出问题:同学们刚圈出即参加跳绳又参加踢毽的同学的名字,他们只是一个人大家有什么办法让这三位同学即在跳绳的圈里又在踢毽组的圈里?
让学生到黑板操作如何摆放集合圈
预设:
提出问题:中间重叠部分表示什么?整个图表示什么?
预设:中间表示既参加跳绳比赛又参加踢毽比赛的同学。
追加问题:整个图表示什么?
预设:参加这两项比赛的同学;参加跳绳比赛或参加踢毽比赛的同学。
提出问题:参加跳绳的学生有9人,参加踢毽的学生有8人,两项有17人,真有17人么?
预设:既参加跳绳又参加踢毽的学生有3人,3人重复,不是17人。
追加问题:那到底有几人参加比赛呢?
预设:14人,9+8-3=14(人)
追问:这一算式表达什么含义?
预设:参加人数=项目人数和-重复人数
小结:在计算总人数时,要记得找出重复的人数,计算时,要把重复的人数减去。
设计意图:在画一画的过程中,学生体脑结合,手脑并用,共同交流、思考,经历了创作的过程,得到了成功的体验。也从中感受到了愉悦、轻松、快活。他们发现问题、解决问题的能力得以进一步发展。
练一练。
巩固练习
1.
三年级有20个同学参加竞赛,其中参加数学竞赛的有15人,参加作文竞赛的有11人。
(1)既参加数学竞赛又参加作文竞赛的有几人?
(2)只参加数学竞赛的有几人?
(3)只参加作文竞赛的有几人?
答案:
(1)15+11-20=6(人)
(2)15-6=9(人)
(3)11-6=5(人)
2.
学校举行乒乓球比赛,A组、B组两个小组各有16人,每组两人一对进行比赛,负者被淘汰、胜者进入下一轮,最后两组第一名进行决赛。两个小组赛一共要进行多少场比赛?
(8+4+2+1)×2=30(场)
答:两个小组赛一共要进行30场比赛。
3.
估计三(3)班可能有多少同学参加比赛。
讨论根据学校要求,每班要选拔9人参加跳绳,8人参加踢毽子比赛,你觉得三(3)班可能会选拔多少人?
判断:①参赛的同学最多有17人()②参赛的同学最少有8人。(
)
预设:得出参赛同学最多是17人,没有人重复:最少有9人,其中8人重复。
设计意图:设计组由梯度的练习,从简单应用到开放,从正向思维到逆向思维,既链接所学知识资源,又实现对学生思维的拓展。这样的练习设计不仅能让学生结合集合思想。
四、课堂小结
提出问题:说一说这节课你们都有什么收获,自己学到了些什么呢?
预设:解决重叠问题,可以从条件入手进行分析,画出示意图,借助示意图进行思考,当两个计数部分有重复包含时,为了不重复地计数,应从他们的和中减去重复部分。
设计意图:培养学生自己概括总结,使学生体会到成功的快乐。
五、拓展延伸
借助拓展知识,使学生增强对钟表知识的认识和学习的兴趣。
1
/
3
教学目标:
1.
通过观察、猜测、操作、交流等活动,让学生在自主探究活动中感知集合图形成的过程,体会集合图的优点。
2.
能借助直观图,用集合图分析并解决生活中简单的有重复部分的问题。
3.
渗透多种方法解决重叠问题的意识,培养学生善于观察、勤于思考的学习习惯。
教学重点:
理解集合图各部分的意义,能用集合图分析生活中简单的有重复部分的问题。
教学难点:
使学生会借助直观图,利用集合的思想方法解决简单的实际问题。
教学过程:
游戏导入
“脑筋急转弯”游戏:房间里有两个爸爸,两个儿子,但是只有三个人,这是怎么回事?(强调爸爸身份的双重性——身份重复了)
预设:这三个人是儿子、爸爸、爷爷。
设计意图:通过学生喜爱的脑筋急转弯引入,激发了学生无限的学习兴趣,同时引导学生大胆的猜想,让学生在猜测中学会思考,在争论中学会倾听、学会交流、学会整合。
探究新知
课件出示三(1)班参加跳绳、踢毽比赛的学生名单。
提出问题:有几个人参加跳绳比赛?有几个人参加踢毽比赛?
预设:参加跳绳的有9人,参加踢毽子的有8人。
提出问题:观察表格内容,你有什么发现呢?
预设:有些人的名字是重复的。
提出问题:哪些人?有没有什么办法,能清楚地看出有三人重复呢?
提出要求:把重复的人名圈出来,用表格整理出来。
跳绳
杨明
刘红
李芳
陈东
王爱华
马超
丁旭
赵军
徐强
踢毽
于丽
周晓
朱晓东
陶伟
卢强
?
教师说明:同学们现在表格人数比较少容易找人名,但是表格人多时就不好找了。那我们今天就来用集合的方法来解决这一问题。
提出要求:老师把两个圈都贴在黑板上了,请两位同学来帮老师把两组参赛的同学人名分别贴在黑板上两个圈里面。
两个学生操作!
预设:
提出问题:同学们刚圈出即参加跳绳又参加踢毽的同学的名字,他们只是一个人大家有什么办法让这三位同学即在跳绳的圈里又在踢毽组的圈里?
让学生到黑板操作如何摆放集合圈
预设:
提出问题:中间重叠部分表示什么?整个图表示什么?
预设:中间表示既参加跳绳比赛又参加踢毽比赛的同学。
追加问题:整个图表示什么?
预设:参加这两项比赛的同学;参加跳绳比赛或参加踢毽比赛的同学。
提出问题:参加跳绳的学生有9人,参加踢毽的学生有8人,两项有17人,真有17人么?
预设:既参加跳绳又参加踢毽的学生有3人,3人重复,不是17人。
追加问题:那到底有几人参加比赛呢?
预设:14人,9+8-3=14(人)
追问:这一算式表达什么含义?
预设:参加人数=项目人数和-重复人数
小结:在计算总人数时,要记得找出重复的人数,计算时,要把重复的人数减去。
设计意图:在画一画的过程中,学生体脑结合,手脑并用,共同交流、思考,经历了创作的过程,得到了成功的体验。也从中感受到了愉悦、轻松、快活。他们发现问题、解决问题的能力得以进一步发展。
练一练。
巩固练习
1.
三年级有20个同学参加竞赛,其中参加数学竞赛的有15人,参加作文竞赛的有11人。
(1)既参加数学竞赛又参加作文竞赛的有几人?
(2)只参加数学竞赛的有几人?
(3)只参加作文竞赛的有几人?
答案:
(1)15+11-20=6(人)
(2)15-6=9(人)
(3)11-6=5(人)
2.
学校举行乒乓球比赛,A组、B组两个小组各有16人,每组两人一对进行比赛,负者被淘汰、胜者进入下一轮,最后两组第一名进行决赛。两个小组赛一共要进行多少场比赛?
(8+4+2+1)×2=30(场)
答:两个小组赛一共要进行30场比赛。
3.
估计三(3)班可能有多少同学参加比赛。
讨论根据学校要求,每班要选拔9人参加跳绳,8人参加踢毽子比赛,你觉得三(3)班可能会选拔多少人?
判断:①参赛的同学最多有17人()②参赛的同学最少有8人。(
)
预设:得出参赛同学最多是17人,没有人重复:最少有9人,其中8人重复。
设计意图:设计组由梯度的练习,从简单应用到开放,从正向思维到逆向思维,既链接所学知识资源,又实现对学生思维的拓展。这样的练习设计不仅能让学生结合集合思想。
四、课堂小结
提出问题:说一说这节课你们都有什么收获,自己学到了些什么呢?
预设:解决重叠问题,可以从条件入手进行分析,画出示意图,借助示意图进行思考,当两个计数部分有重复包含时,为了不重复地计数,应从他们的和中减去重复部分。
设计意图:培养学生自己概括总结,使学生体会到成功的快乐。
五、拓展延伸
借助拓展知识,使学生增强对钟表知识的认识和学习的兴趣。
1
/
3
