人教版九下:27.2.1 相似三角形的判定 教案
文档属性
| 名称 | 人教版九下:27.2.1 相似三角形的判定 教案 |
|
|
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-08 00:00:00 | ||
图片预览


文档简介
相似三角形的判定
教学目标:1、通过探索,掌握相似三角形的判定方法。
2、运用相似三角形的判定方法解决数学问题。
3、通过解题的引申练习,培养学生练习后反思的好习惯。
教学重点:判定三角形相似的方法
教学难点:运用相似三角形的判定方法解决数学问题。
回忆复习
_________________________________的两个三角形, 叫做相似三角形
相似三角形的特征:________________________。
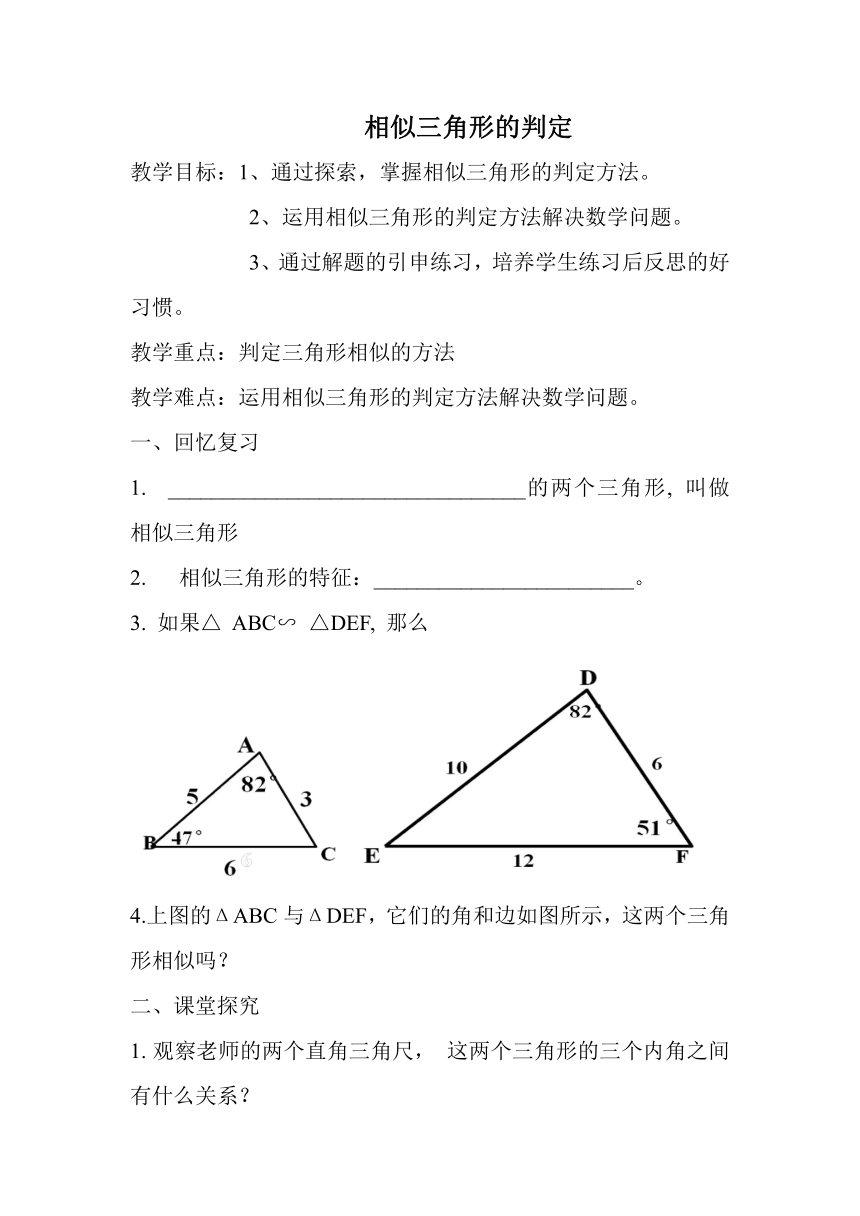
如果△ ABC∽ △DEF, 那么
4.上图的ΔABC与ΔDEF,它们的角和边如图所示,这两个三角形相似吗?
课堂探究
观察老师的两个直角三角尺, 这两个三角形的三个内角之间有什么关系?
从直观上看,这两个三角形相似吗? 三个内角对应相等的两个三角形一定相似吗?
动手操作: 画一个三角形,使三个角分别为60°,45°, 75° 。
①用刻度尺量出这个三角形三边的长度;②看看与同桌的三角形的对应边是否成比例.
结论:
用数学符号表示:
判断
1)、两个等边三角形相似 ( )
2)、两个直角三角形相似 ( )
3)、两个等腰直角三角形都相似( )
4)、有一个角为50°的两个等腰三角形相似( )
5)、有一个角为100°的两个等腰三角形相似( )
5.例题:例1、已知:ΔABC和ΔDEF中, ∠A=40°,∠B=80°,∠E=80°, ∠F=60°。求证:ΔABC∽ΔDEF
练习 :已知:ΔABC和ΔDEF中, ∠A=46°,∠B=74°,
∠D=60°, ∠E=74°。这两个三角形相似吗?请说明理由。
例2、△ABC 中, D是AB上的点,且 ∠ACD=∠B,试说明 (1)△ABC与△ADC相似 (2)AB·AD=AC 2
(3)AD=4,AC=6,求AB。
变式:在△ABC 中, D、E 分别是AB、 AC上的点,且 DE∥BC,试说明(1)△ABC与△ADE相似。
(2)AD·AC=AE·AB(3)若AD=4,AE=3,AB=6,求AC
练习:找出右上图中所有的相似三角形
总结:本节课你认为应该要掌握什么?你有什么收获?
四、作业布置:
五、拓展题:如图,△ABC中,DE∥BC,EF∥AB,
1) 求证: △ADE∽△EFC.
2)图中还有相似三角形吗?若有请找出来。
3)如果点D恰好是边AB的中点,那么点E是边AC的中点吗?DE和BC又有什么关系呢?
教学目标:1、通过探索,掌握相似三角形的判定方法。
2、运用相似三角形的判定方法解决数学问题。
3、通过解题的引申练习,培养学生练习后反思的好习惯。
教学重点:判定三角形相似的方法
教学难点:运用相似三角形的判定方法解决数学问题。
回忆复习
_________________________________的两个三角形, 叫做相似三角形
相似三角形的特征:________________________。
如果△ ABC∽ △DEF, 那么
4.上图的ΔABC与ΔDEF,它们的角和边如图所示,这两个三角形相似吗?
课堂探究
观察老师的两个直角三角尺, 这两个三角形的三个内角之间有什么关系?
从直观上看,这两个三角形相似吗? 三个内角对应相等的两个三角形一定相似吗?
动手操作: 画一个三角形,使三个角分别为60°,45°, 75° 。
①用刻度尺量出这个三角形三边的长度;②看看与同桌的三角形的对应边是否成比例.
结论:
用数学符号表示:
判断
1)、两个等边三角形相似 ( )
2)、两个直角三角形相似 ( )
3)、两个等腰直角三角形都相似( )
4)、有一个角为50°的两个等腰三角形相似( )
5)、有一个角为100°的两个等腰三角形相似( )
5.例题:例1、已知:ΔABC和ΔDEF中, ∠A=40°,∠B=80°,∠E=80°, ∠F=60°。求证:ΔABC∽ΔDEF
练习 :已知:ΔABC和ΔDEF中, ∠A=46°,∠B=74°,
∠D=60°, ∠E=74°。这两个三角形相似吗?请说明理由。
例2、△ABC 中, D是AB上的点,且 ∠ACD=∠B,试说明 (1)△ABC与△ADC相似 (2)AB·AD=AC 2
(3)AD=4,AC=6,求AB。
变式:在△ABC 中, D、E 分别是AB、 AC上的点,且 DE∥BC,试说明(1)△ABC与△ADE相似。
(2)AD·AC=AE·AB(3)若AD=4,AE=3,AB=6,求AC
练习:找出右上图中所有的相似三角形
总结:本节课你认为应该要掌握什么?你有什么收获?
四、作业布置:
五、拓展题:如图,△ABC中,DE∥BC,EF∥AB,
1) 求证: △ADE∽△EFC.
2)图中还有相似三角形吗?若有请找出来。
3)如果点D恰好是边AB的中点,那么点E是边AC的中点吗?DE和BC又有什么关系呢?
