人教版九下:27.2.1 相似三角形的判定 教案(表格式)
文档属性
| 名称 | 人教版九下:27.2.1 相似三角形的判定 教案(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 90.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-08 00:00:00 | ||
图片预览


文档简介
教学设计方案模板:
教学设计方案
课题名称:相似三角形的判定定理2
姓名:
teacher
工作单位:
学科年级:
九年级数学
教材版本:
人教课标版
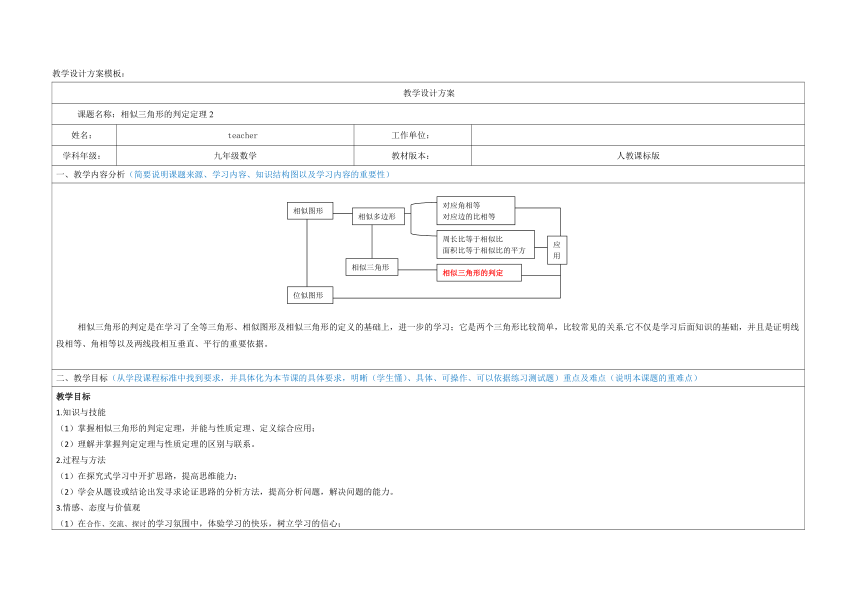
一、教学内容分析(简要说明课题来源、学习内容、知识结构图以及学习内容的重要性)
相似图形
相似多边形
相似三角形
位似图形
对应角相等
对应边的比相等
周长比等于相似比
面积比等于相似比的平方
相似三角形的判定
应用
相似三角形的判定是在学习了全等三角形、相似图形及相似三角形的定义的基础上,进一步的学习;它是两个三角形比较简单,比较常见的关系.它不仅是学习后面知识的基础,并且是证明线段相等、角相等以及两线段相互垂直、平行的重要依据。
二、教学目标(从学段课程标准中找到要求,并具体化为本节课的具体要求,明晰(学生懂)、具体、可操作、可以依据练习测试题)重点及难点(说明本课题的重难点)
教学目标
1.知识与技能
(1)掌握相似三角形的判定定理,并能与性质定理、定义综合应用;
(2)理解并掌握判定定理与性质定理的区别与联系。
2.过程与方法
(1)在探究式学习中开扩思路,提高思维能力;
(2)学会从题设或结论出发寻求论证思路的分析方法,提高分析问题,解决问题的能力。
3.情感、态度与价值观
(1)在合作、交流、探讨的学习氛围中,体验学习的快乐,树立学习的信心;
(2)通过学习,体会几何证明的方法美。
教学难点、重点
1.重点:掌握判定定理,会运用判定定理判定两个三角形相似。
2.难点:
(1)找相似三角形的对应边。
(2)会准确的运用两个三角形相似的条件来判定两个三角形是否相似。
三、学习者特征分析(学生对预备知识的掌握了解情况,学生在新课的学习方法的掌握情况,如何设计预习)
1.九年级学生已经具备了一定的图形之间的关系的认识。
2.学生的思维在合理推理向演绎推理的过渡阶段。
3.经历过探索全等三角形判定,通过类比不难得到相似三角形的判定。
四、教学过程(设计本课的学习环节,明确各环节的子目标,画出流程图)
复习提问 →引入新课课
→定理应用→课后巩固
2023745-1351915提出问题
引入定理2
证明定理2
3255645-1649095
五、教学策略选择与信息技术融合的设计(针对学习流程的设计的各流程,设计教与学的方式的变革,配置学习资源和数字化工具,设计信息技术融合点)
教师活动
预设学生活动
设计意图
(一)复习提问
问题:(1)相似三角形的定义是什么?
(2) 判断两个三角形相似,你有哪些方法?
学生回答 对应边成比例,对应角相等的两个三角形相似。
学生1回答 方法1:通过定义 (不常用);
学生2回答 方法2:通过平行线(条件特殊,使用起来有局限性);
学生3回答 方法3:判定定理1 即如果两个三角形的三组对应边的比相等, 那么这两个三角形相似。
引导学生复习学过的知识,承前启后,激发学生学习新知的欲望。
引入新课
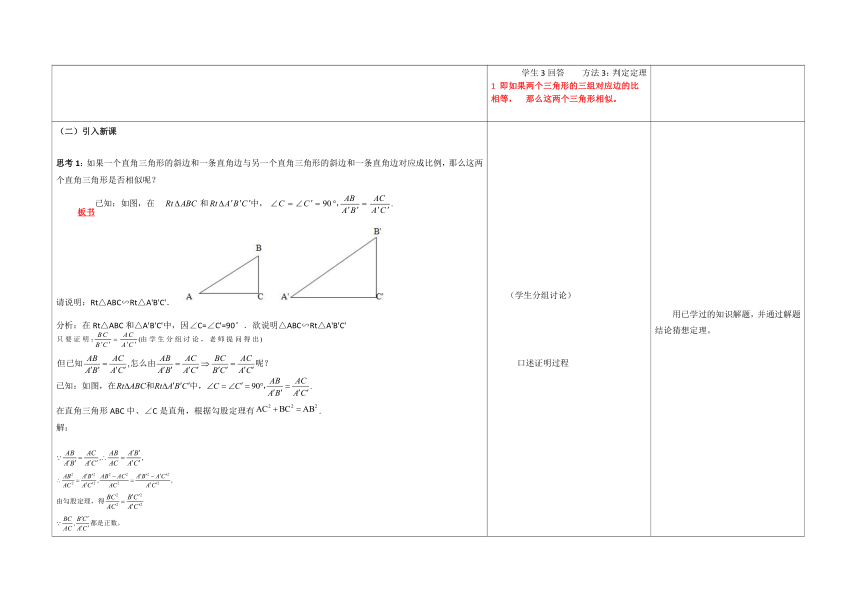
思考1:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形是否相似呢?
板书
请说明:Rt△ABC∽Rt△A'B'C'.
分析:在Rt△ABC和△A'B'C'中,因∠C=∠C'=90°.欲说明△ABC∽Rt△A'B'C'
在直角三角形ABC中、∠C是直角,根据勾股定理有.
解:
∴ΔABC~ΔA'B'C'
思考题1 可以得出:
定理2 如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
(学生分组讨论)
口述证明过程
用已学过的知识解题,并通过解题结论猜想定理。
证明定理 板书
.
证明:过点B'在B'A'上取线段AB的长,同理过点B'在B'C'上取线段BC的长,连接AC。
得到如图3所示,∵则AC//A'C'
∴,,
∴ΔABCΔA'B'C'。
应用已学的知识证明定理。
(四)定理应用
板书 例1 在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90?,AC=4,BC=5,A'C'=8,B'C'=10。
故△ABC∽△A'B'C'.
板书 例2已知:如图,在四边形ABCD中,∠B=∠ACD,AB=6,BC=4,AC=5,CD=,求AD的长.
分析:由已知一对对应角相等及四条边长,猜想应用“两组对应边的比相等且它们的夹角相等”来证明.计算得出,结合∠B=∠ACD,证明△ABC∽△DCA,再利用相似三角形的定义得出关于AD的比例式,从而求出AD的长.
解:
学生分组讨论,每组找一个代表讲述证明过程
两个学生板练,其他学生自己练习
(1)能够运用所学的判定方法解决简单问题;
(2)通过数、形两个例题的设置,让学生体会判定定理。
五、布置作业 (已印刷出来)
1.判断正误:对的画“√”,错的画“×”.
(1)两个全等三角形一定相似; ( )
(2)两个相似三角形一定全等; ( )
(3)两个等腰三角形一定相似; ( )
(4)顶角相等的两个等腰三角形一定相似; ( )
(5)两个直角三角形一定相似; ( )
(6)有一个锐角对应相等的两个直角三角形一定相似; ( )
(7)两个等腰直角三角形一定相似; ( )
(8)两个等边三角形一定相似. ( )
2.填空:
(1)如图1,BE∥CD,则△ ∽△ ,
;
(2)如图2,AB∥DE,则△ ∽△ ,
;
(3)如图3,∠B=∠ADE,则△ ∽△ ,
.
独立完成。
了解学生对本节课内容的掌握情况,及强化基本技能的训练。
六、教学评价设计(创建量规,向学生展示他们将被如何评价(来自教师和小组其他成员的评价)。也可以创建一个自我评价表,这样学生可以用它对自己的学习进行评价)
三维目标(学生评价,按三个标准评价:很大提升选A 有新的认识,但还需课后补充选B,没什么改变选C)
知识与技能
7905750-6350(1)掌握相似三角形的判定定理,并能与性质定理、定义综合应用;
(2)理解并掌握判定定理与性质定理的区别与联系。
过程与方法
(3)在探究式学习中开扩思路,提高思维能力;
(4)学会从题设或结论出发寻求论证思路的分析方法,提高分析问题,解决问题的能力。
情感、态度与价值观
(5)在合作、交流、探讨的学习氛围中,体验学习的快乐,树立学习的信心;
(6)通过学习,体会几何证明的方法美。
教学难点、重点(自我评价)
1.重点:掌握判定定理,会运用判定定理判定两个三角形相似。
2.难点:
(1)找相似三角形的对应边。
(2)会准确的运用两个三角形相似的条件来判定两个三角形是否相似。
七、教学板书(本节课的教学板书)
在教学过程中已体现(红色部分)
附录:评价表
A
B
C
(1)
(2)
(3)
(4)
(5)
(6)
重点突出
难点突破
教学设计方案
课题名称:相似三角形的判定定理2
姓名:
teacher
工作单位:
学科年级:
九年级数学
教材版本:
人教课标版
一、教学内容分析(简要说明课题来源、学习内容、知识结构图以及学习内容的重要性)
相似图形
相似多边形
相似三角形
位似图形
对应角相等
对应边的比相等
周长比等于相似比
面积比等于相似比的平方
相似三角形的判定
应用
相似三角形的判定是在学习了全等三角形、相似图形及相似三角形的定义的基础上,进一步的学习;它是两个三角形比较简单,比较常见的关系.它不仅是学习后面知识的基础,并且是证明线段相等、角相等以及两线段相互垂直、平行的重要依据。
二、教学目标(从学段课程标准中找到要求,并具体化为本节课的具体要求,明晰(学生懂)、具体、可操作、可以依据练习测试题)重点及难点(说明本课题的重难点)
教学目标
1.知识与技能
(1)掌握相似三角形的判定定理,并能与性质定理、定义综合应用;
(2)理解并掌握判定定理与性质定理的区别与联系。
2.过程与方法
(1)在探究式学习中开扩思路,提高思维能力;
(2)学会从题设或结论出发寻求论证思路的分析方法,提高分析问题,解决问题的能力。
3.情感、态度与价值观
(1)在合作、交流、探讨的学习氛围中,体验学习的快乐,树立学习的信心;
(2)通过学习,体会几何证明的方法美。
教学难点、重点
1.重点:掌握判定定理,会运用判定定理判定两个三角形相似。
2.难点:
(1)找相似三角形的对应边。
(2)会准确的运用两个三角形相似的条件来判定两个三角形是否相似。
三、学习者特征分析(学生对预备知识的掌握了解情况,学生在新课的学习方法的掌握情况,如何设计预习)
1.九年级学生已经具备了一定的图形之间的关系的认识。
2.学生的思维在合理推理向演绎推理的过渡阶段。
3.经历过探索全等三角形判定,通过类比不难得到相似三角形的判定。
四、教学过程(设计本课的学习环节,明确各环节的子目标,画出流程图)
复习提问 →引入新课课
→定理应用→课后巩固
2023745-1351915提出问题
引入定理2
证明定理2
3255645-1649095
五、教学策略选择与信息技术融合的设计(针对学习流程的设计的各流程,设计教与学的方式的变革,配置学习资源和数字化工具,设计信息技术融合点)
教师活动
预设学生活动
设计意图
(一)复习提问
问题:(1)相似三角形的定义是什么?
(2) 判断两个三角形相似,你有哪些方法?
学生回答 对应边成比例,对应角相等的两个三角形相似。
学生1回答 方法1:通过定义 (不常用);
学生2回答 方法2:通过平行线(条件特殊,使用起来有局限性);
学生3回答 方法3:判定定理1 即如果两个三角形的三组对应边的比相等, 那么这两个三角形相似。
引导学生复习学过的知识,承前启后,激发学生学习新知的欲望。
引入新课
思考1:如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形是否相似呢?
板书
请说明:Rt△ABC∽Rt△A'B'C'.
分析:在Rt△ABC和△A'B'C'中,因∠C=∠C'=90°.欲说明△ABC∽Rt△A'B'C'
在直角三角形ABC中、∠C是直角,根据勾股定理有.
解:
∴ΔABC~ΔA'B'C'
思考题1 可以得出:
定理2 如果两个三角形的两组对应边的比相等,并且相应的夹角相等,那么这两个三角形相似.
(学生分组讨论)
口述证明过程
用已学过的知识解题,并通过解题结论猜想定理。
证明定理 板书
.
证明:过点B'在B'A'上取线段AB的长,同理过点B'在B'C'上取线段BC的长,连接AC。
得到如图3所示,∵则AC//A'C'
∴,,
∴ΔABCΔA'B'C'。
应用已学的知识证明定理。
(四)定理应用
板书 例1 在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90?,AC=4,BC=5,A'C'=8,B'C'=10。
故△ABC∽△A'B'C'.
板书 例2已知:如图,在四边形ABCD中,∠B=∠ACD,AB=6,BC=4,AC=5,CD=,求AD的长.
分析:由已知一对对应角相等及四条边长,猜想应用“两组对应边的比相等且它们的夹角相等”来证明.计算得出,结合∠B=∠ACD,证明△ABC∽△DCA,再利用相似三角形的定义得出关于AD的比例式,从而求出AD的长.
解:
学生分组讨论,每组找一个代表讲述证明过程
两个学生板练,其他学生自己练习
(1)能够运用所学的判定方法解决简单问题;
(2)通过数、形两个例题的设置,让学生体会判定定理。
五、布置作业 (已印刷出来)
1.判断正误:对的画“√”,错的画“×”.
(1)两个全等三角形一定相似; ( )
(2)两个相似三角形一定全等; ( )
(3)两个等腰三角形一定相似; ( )
(4)顶角相等的两个等腰三角形一定相似; ( )
(5)两个直角三角形一定相似; ( )
(6)有一个锐角对应相等的两个直角三角形一定相似; ( )
(7)两个等腰直角三角形一定相似; ( )
(8)两个等边三角形一定相似. ( )
2.填空:
(1)如图1,BE∥CD,则△ ∽△ ,
;
(2)如图2,AB∥DE,则△ ∽△ ,
;
(3)如图3,∠B=∠ADE,则△ ∽△ ,
.
独立完成。
了解学生对本节课内容的掌握情况,及强化基本技能的训练。
六、教学评价设计(创建量规,向学生展示他们将被如何评价(来自教师和小组其他成员的评价)。也可以创建一个自我评价表,这样学生可以用它对自己的学习进行评价)
三维目标(学生评价,按三个标准评价:很大提升选A 有新的认识,但还需课后补充选B,没什么改变选C)
知识与技能
7905750-6350(1)掌握相似三角形的判定定理,并能与性质定理、定义综合应用;
(2)理解并掌握判定定理与性质定理的区别与联系。
过程与方法
(3)在探究式学习中开扩思路,提高思维能力;
(4)学会从题设或结论出发寻求论证思路的分析方法,提高分析问题,解决问题的能力。
情感、态度与价值观
(5)在合作、交流、探讨的学习氛围中,体验学习的快乐,树立学习的信心;
(6)通过学习,体会几何证明的方法美。
教学难点、重点(自我评价)
1.重点:掌握判定定理,会运用判定定理判定两个三角形相似。
2.难点:
(1)找相似三角形的对应边。
(2)会准确的运用两个三角形相似的条件来判定两个三角形是否相似。
七、教学板书(本节课的教学板书)
在教学过程中已体现(红色部分)
附录:评价表
A
B
C
(1)
(2)
(3)
(4)
(5)
(6)
重点突出
难点突破
