人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)(PPT版+word版)(38张PPT)
文档属性
| 名称 | 人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)(PPT版+word版)(38张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-03 17:57:11 | ||
图片预览











文档简介
(共38张PPT)
人教版六年级数学下册第三章
《圆柱与圆锥》知识讲解及考前押题卷精讲
(第三套)
专题复习课件
知识讲解
01
第一部分 知识讲解
一、圆柱
1、圆柱的形成:圆柱是以长方形的一边为轴旋转而得到的。
圆柱也可以由长方形卷曲而得到。(两种方式:1.以长方形的长为底面周长,宽为高;2.以长方形的宽为底面周长,长为高。其中,第一种方式得到的圆柱体体积较大。)
2、圆柱的高是两个底面之间的距离,一个圆柱有无数条高,他们的数值是相等的
3、圆柱的特征:
(1)底面的特征:圆柱的底面是完全相等的两个圆。
(2)侧面的特征:圆柱的侧面是一个曲面。
(3)高的特征 :圆柱有无数条高
4、圆柱的切割:①横切:切面是圆,表面积增加2倍底面积,即S 增 =2πr2
②竖切(过直径):切面是长方形(如果h=2R,切面为正方形),该长方形的长是圆柱的高,宽是圆柱的底面直径,表面积增加两个长方形的面积,即S增=4rh
第一部分 知识讲解
5、圆柱的侧面展开图:①沿着高展开,展开图形是长方形,如果h=2πr,展开图形为正方形
②不沿着高展开,展开图形是平行四边形或不规则图形
③无论怎么展开都得不到梯形
6、圆柱的相关计算公式:底面积 :S底=πr2
底面周长:C底=πd=2πr
侧面积 :S侧=2πrh
表面积 :S表=2S底+S侧=2πr2+2πrh
体积 :V柱=πr2h
考试常见题型:①已知圆柱的底面积和高, 求圆柱的侧面积,表面积,体积,底面周长
②已知圆柱的底面周长和高,求圆柱的侧面积,表面积,体积,底面积
③已知圆柱的底面周长和体积,求圆柱的侧面积,表面积,高,底面积
④已知圆柱的底面面积和高,求圆柱的侧面积,表面积,体积
第一部分 知识讲解
⑤已知圆柱的侧面积和高, 求圆柱的底面半径,表面积,体积,底面积
以上几种常见题型的解题方法,通常是求出圆柱的底面半径和高,再根据圆柱的相关计算公式进行计算
无盖水桶的表面积 =侧面积+一个底面积
油桶的表面积=侧面积+两个底面积
烟囱通风管的表面积=侧面积
只求侧面积:灯罩、排水管、漆柱、通风管、压路机、卫生纸中轴、薯片盒包装
侧面积+一个底面积:玻璃杯、水桶、笔筒、帽子、游泳池
侧面积+两个底面积:油桶、米桶、罐桶类
二、圆锥
1、圆柱的形成:圆锥是以直角三角形的一直角边为轴旋转而得到的
圆锥也可以由扇形卷曲而得到
第一部分 知识讲解
第一部分 知识讲解
2、圆锥的高是两个顶点与底面之间的距离,与圆柱不同,圆锥只有一条高
3、圆锥的特征:
(1)底面的特征:圆锥的底面一个圆。
(2)侧面的特征:圆锥的侧面是一个曲面。
(3)高的特征 :圆锥有一条高。
4、圆柱的切割:①横切:切面是圆
②竖切(过顶点和直径直径):切面是等腰三角形,该等腰三角形的高是圆锥的高,底是圆锥的底面直径,面积增加两个等腰三角形的面积,即S增=2rh
5、圆锥的相关计算公式:底面积 :S底=πr2
底面周长:C底=πd=2πr
体积:V锥= πr2h
考试常见题型:①已知圆锥的底面积和高,求体积,底面周长
第一部分 知识讲解
②已知圆锥的底面周长和高,求圆锥的体积,底面积
③已知圆锥的底面周长和体积,求圆锥的高,底面积
以上几种常见题型的解题方法,通常是求出圆锥的底面半径和高,再根据圆柱的相关计算公式进行计算。
1、圆柱与圆锥等底等高,圆柱的体积是圆锥的3倍。
2、圆柱与圆锥等底等体积,圆锥的高是圆柱的3倍。
3、圆柱与圆锥等高等体积,圆锥的底面积(注意:是底面积而不是底面半径)是圆柱的3倍。
4、圆柱与圆锥等底等高 ,体积相差 Sh
题型总结
①直接利用公式:分析清楚求的的是表面积,侧面积、底面积、体积
分析清楚半径变化导致底面周长、侧面积、底面积、体积的变化
分析清楚两个圆柱(或两个圆锥)半径、底面积、底面周长、侧面积、表面积、体积之比
第一部分 知识讲解
②圆柱与圆锥关系的转换:包括削成最大体积的问题(正方体,长方体与圆柱圆锥之间)
③横截面的问题
④浸水体积问题:(水面上升部分的体积就是浸入水中物品的体积,等于盛水容积的底面积乘以上升的高度)容积是圆柱或长方体,正方体
⑤等体积转换问题:一个圆柱融化后做成圆锥,或圆柱中的溶液倒入圆锥,都是体积不变的 问题,注意不要乘以
考前押题卷精讲
(全解析)
02
第二部分 学习检测
05
讲解脉络
01
02
03
04
选择题
判断题
填空题
解答题
一.单选题
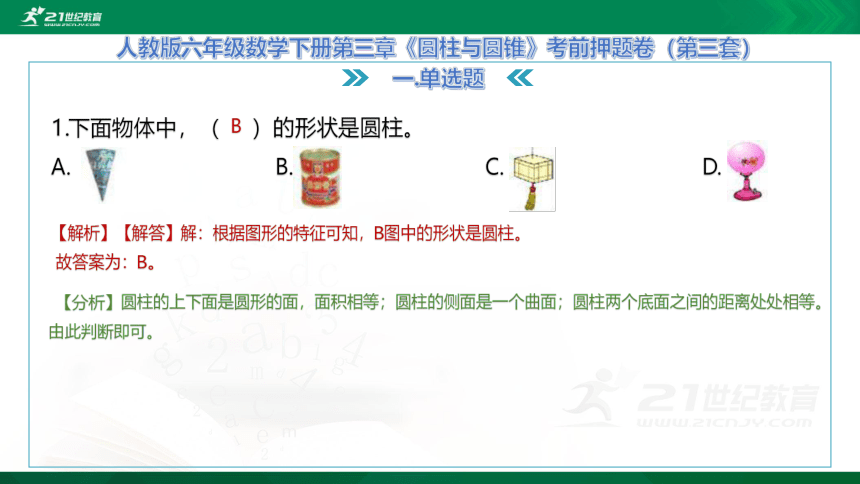
1.下面物体中,( )的形状是圆柱。
A. B. C. D.
B
【解析】【解答】解:根据图形的特征可知,B图中的形状是圆柱。
故答案为:B。
【分析】圆柱的上下面是圆形的面,面积相等;圆柱的侧面是一个曲面;圆柱两个底面之间的距离处处相等。由此判断即可。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
一.单选题
2.一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱高的3倍,圆锥的体积是12立方分米,圆柱的体积是( )立方分米。
A. 12 B. 4 C. 8 D. 36
A
【分析】一个圆柱和一个圆锥的底面直径相等,说明两个图形的底面积相等;由于底面积相等,比较两个图形的大小就取决于高,圆锥的高是圆柱高的3倍,这样圆锥的体积=圆柱的体积× ×3,故圆锥体积=圆柱体积。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
【解析】【解答】解:设圆柱的体积是V1=Sh1。
圆锥的体积V= Sh,当h=3×h1时,V=Sh1=12,故V= 。
故答案为:A。
一.单选题
3.一个圆柱的底面周长是9.42厘米,高是2.5厘米,它的表面积是( )平方厘米。
A.14.13 B.23.55 C.37.68
C
【解析】【解答】解:这个圆柱的底面半径=9.42÷3.14÷2=1.5厘米,那么它的底面面积=1.5×1.5×3.14=7.065平方厘米,侧面积=9.42×2.5=23.55平方厘米,所以这个圆柱的表面积=7.065×2+23.55=37.68平方厘米。
故答案为:C。
【分析】圆柱的表面积=圆柱的侧面积+圆柱的底面积×2,其中圆柱的侧面积=圆柱的底面周长×高,圆柱的底面半径=πr2 , 题目中已经告诉了这个圆柱的底面周长,根据圆的周长公式:圆的周长=2πr,即可求得圆的底面半径。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
一.单选题
4.下面各物体中能用“底面积×高“计算它的体积的物体是( ) A. B. C. D.
D
【分析】观察图可知,圆柱的体积=底面积×高,据此解答。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
【解析】【解答】 选项A, 是不规则物体,体积不能用底面积×高来计算;
选项B, 的体积=底面积×高× ;
选项C, 是不规则物体,体积不能用底面积×高来计算;
选项D, 的体积=底面积×高。
故答案为:D。
6.在如图中,以直线为轴旋转一周,可以得到圆锥体的是( )
A. B. C. D.
5.圆锥的正视图是( )。
A. 三角形 B. 扇形 C. 圆
一.单选题
A
【解析】【解答】 圆锥的正视图是三角形。
故答案为:A。
【分析】圆锥形从正面看,看到的视图是三角形。
【解答】 在如图中,以直线为轴旋转一周,可以得到圆锥体的是 .
故答案为:C.
【分析】直角三角形以一条直角边所在的直线为轴旋转一周,可以得到一个圆锥,据此解答.
C
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
7.小明做了一个圆柱体容器和几个圆锥体容器,尺寸如图所示(单位:cm),将圆柱体内的水倒入( )圆锥体内,正好倒满.
A. B. C.
一.单选题
B
【解答】解:B圆锥和这个圆柱等底等高,所以将圆柱内的水倒入B圆锥中,正好倒满。
故答案为:B。
【分析】圆柱的体积=底面积×高,圆锥的体积=底面积×高×1/3, 等底等高的圆柱体积是圆锥体积的3倍。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
8.把一个体积为9.42立方分米的圆锥放入底面半径为4分米的圆柱形装水容器中(水浸没且无溢出),水面上升了多少分米,列式正确的是( )
A. 9.42÷3÷(3.14×4×4) B. 9.42÷(3.14×4×4)
C. 9.42×3÷(3.14×4×4) D. 9.42×9÷(3.14×4×4)
一.单选题
B
【解析】【解答】 把一个体积为9.42立方分米的圆锥放入底面半径为4分米的圆柱形装水容器中(水浸没且无溢出),水面上升了多少分米,列式正确的是: 9.42÷(3.14×4×4) 。
故答案为:B。
【分析】根据题意可知,先求出圆柱的底面积,然后用圆柱的体积÷圆柱的底面积=上升水面的高度,据此列式解答。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
9.一个圆的直径扩大3倍,那么它的面积扩大( )倍.
A. 3 B. 6 C. 9 D. 4
一.单选题
C
【解析】【解答】解:假设这个圆原来的直径是2厘米,则扩大后是6厘米.
原来圆的面积 S=πr2=3.14×(2÷2)2=3.14(平方厘米)
扩大后圆的面积 S=πr2=3.14×(6÷2)2=28.26(平方厘米)
28.26÷3.14=9
故选:C.
【分析】这道题中圆的直径没有具体说明是几,如果单纯的去算不好算,因此可以采用“假设法”,也就是举例子,在这里我把原来的直径看做2,则扩大后的直径就是(2×3),再根据圆的面积公式分别算出它们的面积,最后用除法算出答案即可.
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
10.下面的说法错误的有( )句。
①圆柱的底面积与高都扩大3倍,它的体积就扩大6倍。
②既是2的倍数又是5的倍数的数的特征是个位必须是0。
③一条线段绕着它的一个端点旋转120°,形成的图形是圆。
④在长方体上,我们找不到两条既不平行也不相交的线段。
⑤公式S梯=(a+b)h÷2,当a=b时,就是平行四边形的面积计算公式。
A. 1 B. 2 C. 3 D. 4
一.单选题
B
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
一.单选题
【解析】【解答】解:①圆柱的底面积与高都扩大3倍,它的体积就扩大9倍;原来说法错误;
②既是2的倍数又是5的倍数的数的特征是个位必须是0。原来说法正确;
③120÷360=1/3 , 原来说法正确;
④在长方体上,例如前面长方形下面的长与后面长方形的宽就不平行也不相交。原来说法错误;
⑤a=b时,说明上底和下底相等,那么这个图形实际就是一个平行四边形,就是平行四边形的面积计算公式。原来说法正确。
故答案为:B。
【分析】①圆柱的体积=底面积×高,因此体积扩大的倍数是3×3=9;
④长方体相对面不对应的长和宽既不平行也不相交。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
11.从圆锥的顶点到底面圆周上任意一点的距离是圆锥的高。( )
二.判断题
错误
【解析】【解答】解:从圆锥的顶点到底面圆心的距离是圆锥的高。原题说法错误。
故答案为:错误。
【分析】圆锥只有一条高,是圆锥顶点到底面圆心的距离。
12.从圆锥的顶点到底面周长任意一点的连线都是圆锥的高.( )
【解答】 从圆锥的顶点到底面圆心的距离是圆锥的高,原题说法错误.
故答案为:错误.
【分析】 根据圆锥体的高的定义可知:从圆锥顶点到底面圆中心的距离叫做圆锥的高,据此判断.
错误
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
13.一个正方体和一个圆柱体的底面积和高都相等,它们的体积也一定相等.
( )
二.判断题
【解析】【解答】解:一个正方体和一个圆柱体的底面积和高都相等,它们的体积也一定相等。原题说法正确。故答案为:正确。
【分析】正方体体积=底面积×高,圆柱体体积=底面积×高,所以底面积和高都相等的正方体和圆柱体的体积相等。
14.圆柱的侧面展开图可能是正方形。( )
【解析】【解答】解:圆柱的侧面展开图可能是正方形,原题说法正确.
故答案为:正确
【分析】圆柱的侧面展开后是一个长方形或正方形,长方形或正方形的一条边与底面周长相等,另一条边与高相等;当底面周长和高相等时侧面展开就是一个正方形.
正确
正确
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
15.圆锥体的体积是8立方厘米,高是2厘米,底面积是12平方厘米。( )
二.判断题
【解析】【解答】解:8×3÷2=12(平方厘米);
故答案为:正确。
【分析】根据圆锥体的体积公式V=1/3 S底h,可以推导出底面积S=3V÷h,据此代入数据解答即可。
正确
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
16.一个圆柱的侧面展开图是一个正方形,高是25.12 cm,这个圆柱的底面半径是______cm。
三.填空题
4
【解析】【解答】解:由题可知,底面周长=25.12厘米,故底面半径=25.12÷2÷π=25.12÷2÷3.14=4(厘米)。
故答案为:4。
【分析】圆柱侧面展开图是一个以底面圆的周长为一边、高为另一边的一个长方形,若为正方形说明底面周长=高。圆的周长C=2πr。π在计算时一般取3.14。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
17.一个圆锥有________条高,一个圆柱有________条高。
A.一 B.二 C.三 D.无数条
三.填空题
A
【解析】【解答】解:一个圆锥有1条高,一个圆柱有无数条高。
故答案为:A;D。
【分析】圆锥顶点到底面圆心的距离就是圆锥的高,圆锥只有一条高;圆柱两个底面之间的距离就是圆柱的高,圆柱有无数条高。
D
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
18.圆锥的侧面展开图是一个________,将圆锥沿高展开,所得到的横截面是一个______________.
三.填空题
扇形
等腰三角形
【解析】【解答】 圆锥的侧面展开图是一个扇形,将圆锥沿高展开,所得到的横截面是一个等腰三角形.
故答案为:扇形;等腰三角形.
【分析】根据对圆锥的认识可知,圆锥的侧面展开图是一个扇形,将圆锥沿高展开,所得到的横截面是一个等腰三角形.
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
19.圆柱的体积不变,如果底面半径扩大到原来的2倍,那么高应该________.
三.填空题
缩小4倍
【解析】【解答】 圆柱的体积不变,如果底面半径扩大到原来的2倍,那么高应该缩小4倍.
故答案为:缩小4倍.
【分析】根据圆柱的体积公式:V=πr2h,当一个圆柱的体积不变,如果底面半径扩大到原来的a倍,那么高应该缩小a2倍,据此解答.
20.将一个圆柱体的高截短3厘米,此时它的表面积会减少18.84平方厘米,那么它的体积会减少________立方厘米。
【解析】【解答】解:18.84÷3=6.28平方厘米,6.28÷3.14÷2=1厘米,12×3.14×3=9.42立方厘米,所以它的体积会减少9.42立方厘米。故答案为:9.42。
【分析】圆柱体只是把高截短了,底面周长不变,所以圆柱体的底面周长=圆柱体减少的表面积÷圆柱体截短的高,圆柱体的底面半径=圆柱体的底面周长÷π÷2,所以圆柱体减少的体积=πr2×截短的高。
9.42
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
21.想一想,填一填。
一个圆柱的体积是6m3,和它等底等高的圆锥的体积是________ m3 。
三.填空题
2
22.一根长1米的圆木,现将它锯成同样长短的两段,表面积增加了56平方厘米,这根圆木原来的体积是________立方厘米.
【解析】【解答】1米=100厘米;
56÷2=28(平方厘米);
28×100=2800(立方厘米).
故答案为:2800.
【分析】根据1米=100厘米,先将单位化统一,将一根圆木锯成同样长短的两段,表面积增加了2个底面积,用增加的表面积÷2=圆柱的底面积,然后用圆柱的底面积×高=圆柱的体积,据此列式解答.
2800
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
【解析】【解答】6× =2(立方米)
【分析】等底等高的圆锥的体积是圆柱的体积的 ,所以可用圆柱的体积乘 即可得到圆锥的体积。
23.一个圆柱削去2.4立方米后,正好削成一个与它等底等高的圆锥,削成的这个圆锥的体积是________立方米,圆柱原来的体积是________立方米。
三.填空题
1.2
【解析】【解答】圆锥的体积:2.4÷2=1.2(立方米);
圆柱的体积:1.2×3=3.6(立方米).
故答案为:1.2;3.6 。
【分析】根据题意可知,将一个圆柱削成一个等底等高的圆锥,削去部分的体积是圆锥体积的2倍,据此用削去部分的体积÷2=圆锥的体积,等底等高的圆柱体积是圆锥体积的3倍,用圆锥的体积×3=圆柱的体积,据此列式解答.
3.6
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
24.圆锥有________条高,是________和____________的连线。
三.填空题
1
【解答】1;顶点;底面圆心
顶点
底面圆心
25.等底等高的圆柱和圆锥,它们的体积一共是60立方米,那么圆锥体积是________立方米。
【解析】【解答】等底等高的圆柱和圆锥,它们的体积比是3:1,所以圆锥的体积是总体积的,所以圆锥的体积是60×=15
15
【分析】等底等高的圆柱和圆锥,它们的体积比是3:1,按照按比例分配解题的方法即可解答。
【解析】根据圆锥特点,辨别圆锥,了解它的组成部分,界定它的组成部分的概念。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
26.李师傅做了50个直经是8dm高是12dm的圆柱形铁桶,每1dm2的铁桶重6.5kg,做好这些铁桶应该用多少千克的铁皮?
四.解答题
【答案】 解:底面积:3.14×(8÷2)2
=3.14×16
=50.24(平方分米)
侧面积:3.14×8×12
=3.14×96
=301.44(平方分米)
【分析】根据题意可知,先求出每个无盖圆柱形铁桶的表面积,然后用每个无盖铁桶的表面积×制作的铁桶的个数×每立方分米铁桶的质量=一共需要的质量,据此列式解答。
需要铁皮重量:
(50.24+301.44)×50×6.5
=351.68×325
=114296(千克)
答:做好这些铁桶应该用114296千克的铁皮。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
27.一个酒瓶里面深30cm,底面内直径是10cm,瓶里酒深15cm。把瓶口塞紧后使其瓶口向下倒立,这时酒深25cm。求酒瓶的容积。
四.解答题
【答案】 解:3.14×(10÷2)2×[15+(30-25)]=1570(cm3)
答:酒瓶的容积是1570 cm3。
【分析】酒瓶的容积相当于高15厘米的圆柱形酒的体积,和高是(30-25)厘米的圆柱形空气的体积,把这两部分体积相加就是酒瓶的容积。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
28.一个圆锥形沙滩,底面周长是21.98m,高1.2m。如果每立方米沙重1.5t,这堆沙重多少吨
四.解答题
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
【答案】解:3.14×(21.98 ÷6.28) ×1.2× ×1.5
=15.386×1.5
=23.079(吨)
答:这堆沙重23.079吨
【分析】圆锥的体积= ×底面积×高。高已知,根据底面周长求出半径,根据半径求出底面积;沙重=圆锥体积×1.5吨,据此可求解。
29.小组同学在一起找一个圆锥形的物体(一堆沙子等),想办法计算出它的体积.
四.解答题
【答案】解:可以测量出圆锥的底面周长和高,用底面周长除以3.14,再除以2求出底面半径,然后用底面积乘高乘即可求出推体积.
【解析】【分析】测量底面的半径有难度,可以通过测量底面周长来计算出底面半径,再测量出高;然后根据公式计算,圆锥的体积=底面积×高×1/3.
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
30.学校绘画组一共有48人,如果每组6人,可以分成多少组?如果要平均分成4组,每组有多少人?
四.解答题
【答案】 解:48÷6=8(组)
48÷4=12(人)
答:如果每组6人,可以分成8组,如果要平均分成4组,每组有12人。
【解析】【分析】如果每组6人,可以分成的组数=绘画组的总人数÷6;如果平均分成4组,每组的人数=绘画组的总人数÷4。据此代入数据作答即可。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
谢谢您的观看!
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
人教版六年级数学下册第三章
《圆柱与圆锥》知识讲解及考前押题卷精讲
(第三套)
专题复习课件
知识讲解
01
第一部分 知识讲解
一、圆柱
1、圆柱的形成:圆柱是以长方形的一边为轴旋转而得到的。
圆柱也可以由长方形卷曲而得到。(两种方式:1.以长方形的长为底面周长,宽为高;2.以长方形的宽为底面周长,长为高。其中,第一种方式得到的圆柱体体积较大。)
2、圆柱的高是两个底面之间的距离,一个圆柱有无数条高,他们的数值是相等的
3、圆柱的特征:
(1)底面的特征:圆柱的底面是完全相等的两个圆。
(2)侧面的特征:圆柱的侧面是一个曲面。
(3)高的特征 :圆柱有无数条高
4、圆柱的切割:①横切:切面是圆,表面积增加2倍底面积,即S 增 =2πr2
②竖切(过直径):切面是长方形(如果h=2R,切面为正方形),该长方形的长是圆柱的高,宽是圆柱的底面直径,表面积增加两个长方形的面积,即S增=4rh
第一部分 知识讲解
5、圆柱的侧面展开图:①沿着高展开,展开图形是长方形,如果h=2πr,展开图形为正方形
②不沿着高展开,展开图形是平行四边形或不规则图形
③无论怎么展开都得不到梯形
6、圆柱的相关计算公式:底面积 :S底=πr2
底面周长:C底=πd=2πr
侧面积 :S侧=2πrh
表面积 :S表=2S底+S侧=2πr2+2πrh
体积 :V柱=πr2h
考试常见题型:①已知圆柱的底面积和高, 求圆柱的侧面积,表面积,体积,底面周长
②已知圆柱的底面周长和高,求圆柱的侧面积,表面积,体积,底面积
③已知圆柱的底面周长和体积,求圆柱的侧面积,表面积,高,底面积
④已知圆柱的底面面积和高,求圆柱的侧面积,表面积,体积
第一部分 知识讲解
⑤已知圆柱的侧面积和高, 求圆柱的底面半径,表面积,体积,底面积
以上几种常见题型的解题方法,通常是求出圆柱的底面半径和高,再根据圆柱的相关计算公式进行计算
无盖水桶的表面积 =侧面积+一个底面积
油桶的表面积=侧面积+两个底面积
烟囱通风管的表面积=侧面积
只求侧面积:灯罩、排水管、漆柱、通风管、压路机、卫生纸中轴、薯片盒包装
侧面积+一个底面积:玻璃杯、水桶、笔筒、帽子、游泳池
侧面积+两个底面积:油桶、米桶、罐桶类
二、圆锥
1、圆柱的形成:圆锥是以直角三角形的一直角边为轴旋转而得到的
圆锥也可以由扇形卷曲而得到
第一部分 知识讲解
第一部分 知识讲解
2、圆锥的高是两个顶点与底面之间的距离,与圆柱不同,圆锥只有一条高
3、圆锥的特征:
(1)底面的特征:圆锥的底面一个圆。
(2)侧面的特征:圆锥的侧面是一个曲面。
(3)高的特征 :圆锥有一条高。
4、圆柱的切割:①横切:切面是圆
②竖切(过顶点和直径直径):切面是等腰三角形,该等腰三角形的高是圆锥的高,底是圆锥的底面直径,面积增加两个等腰三角形的面积,即S增=2rh
5、圆锥的相关计算公式:底面积 :S底=πr2
底面周长:C底=πd=2πr
体积:V锥= πr2h
考试常见题型:①已知圆锥的底面积和高,求体积,底面周长
第一部分 知识讲解
②已知圆锥的底面周长和高,求圆锥的体积,底面积
③已知圆锥的底面周长和体积,求圆锥的高,底面积
以上几种常见题型的解题方法,通常是求出圆锥的底面半径和高,再根据圆柱的相关计算公式进行计算。
1、圆柱与圆锥等底等高,圆柱的体积是圆锥的3倍。
2、圆柱与圆锥等底等体积,圆锥的高是圆柱的3倍。
3、圆柱与圆锥等高等体积,圆锥的底面积(注意:是底面积而不是底面半径)是圆柱的3倍。
4、圆柱与圆锥等底等高 ,体积相差 Sh
题型总结
①直接利用公式:分析清楚求的的是表面积,侧面积、底面积、体积
分析清楚半径变化导致底面周长、侧面积、底面积、体积的变化
分析清楚两个圆柱(或两个圆锥)半径、底面积、底面周长、侧面积、表面积、体积之比
第一部分 知识讲解
②圆柱与圆锥关系的转换:包括削成最大体积的问题(正方体,长方体与圆柱圆锥之间)
③横截面的问题
④浸水体积问题:(水面上升部分的体积就是浸入水中物品的体积,等于盛水容积的底面积乘以上升的高度)容积是圆柱或长方体,正方体
⑤等体积转换问题:一个圆柱融化后做成圆锥,或圆柱中的溶液倒入圆锥,都是体积不变的 问题,注意不要乘以
考前押题卷精讲
(全解析)
02
第二部分 学习检测
05
讲解脉络
01
02
03
04
选择题
判断题
填空题
解答题
一.单选题
1.下面物体中,( )的形状是圆柱。
A. B. C. D.
B
【解析】【解答】解:根据图形的特征可知,B图中的形状是圆柱。
故答案为:B。
【分析】圆柱的上下面是圆形的面,面积相等;圆柱的侧面是一个曲面;圆柱两个底面之间的距离处处相等。由此判断即可。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
一.单选题
2.一个圆柱和一个圆锥的底面直径相等,圆锥的高是圆柱高的3倍,圆锥的体积是12立方分米,圆柱的体积是( )立方分米。
A. 12 B. 4 C. 8 D. 36
A
【分析】一个圆柱和一个圆锥的底面直径相等,说明两个图形的底面积相等;由于底面积相等,比较两个图形的大小就取决于高,圆锥的高是圆柱高的3倍,这样圆锥的体积=圆柱的体积× ×3,故圆锥体积=圆柱体积。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
【解析】【解答】解:设圆柱的体积是V1=Sh1。
圆锥的体积V= Sh,当h=3×h1时,V=Sh1=12,故V= 。
故答案为:A。
一.单选题
3.一个圆柱的底面周长是9.42厘米,高是2.5厘米,它的表面积是( )平方厘米。
A.14.13 B.23.55 C.37.68
C
【解析】【解答】解:这个圆柱的底面半径=9.42÷3.14÷2=1.5厘米,那么它的底面面积=1.5×1.5×3.14=7.065平方厘米,侧面积=9.42×2.5=23.55平方厘米,所以这个圆柱的表面积=7.065×2+23.55=37.68平方厘米。
故答案为:C。
【分析】圆柱的表面积=圆柱的侧面积+圆柱的底面积×2,其中圆柱的侧面积=圆柱的底面周长×高,圆柱的底面半径=πr2 , 题目中已经告诉了这个圆柱的底面周长,根据圆的周长公式:圆的周长=2πr,即可求得圆的底面半径。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
一.单选题
4.下面各物体中能用“底面积×高“计算它的体积的物体是( ) A. B. C. D.
D
【分析】观察图可知,圆柱的体积=底面积×高,据此解答。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
【解析】【解答】 选项A, 是不规则物体,体积不能用底面积×高来计算;
选项B, 的体积=底面积×高× ;
选项C, 是不规则物体,体积不能用底面积×高来计算;
选项D, 的体积=底面积×高。
故答案为:D。
6.在如图中,以直线为轴旋转一周,可以得到圆锥体的是( )
A. B. C. D.
5.圆锥的正视图是( )。
A. 三角形 B. 扇形 C. 圆
一.单选题
A
【解析】【解答】 圆锥的正视图是三角形。
故答案为:A。
【分析】圆锥形从正面看,看到的视图是三角形。
【解答】 在如图中,以直线为轴旋转一周,可以得到圆锥体的是 .
故答案为:C.
【分析】直角三角形以一条直角边所在的直线为轴旋转一周,可以得到一个圆锥,据此解答.
C
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
7.小明做了一个圆柱体容器和几个圆锥体容器,尺寸如图所示(单位:cm),将圆柱体内的水倒入( )圆锥体内,正好倒满.
A. B. C.
一.单选题
B
【解答】解:B圆锥和这个圆柱等底等高,所以将圆柱内的水倒入B圆锥中,正好倒满。
故答案为:B。
【分析】圆柱的体积=底面积×高,圆锥的体积=底面积×高×1/3, 等底等高的圆柱体积是圆锥体积的3倍。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
8.把一个体积为9.42立方分米的圆锥放入底面半径为4分米的圆柱形装水容器中(水浸没且无溢出),水面上升了多少分米,列式正确的是( )
A. 9.42÷3÷(3.14×4×4) B. 9.42÷(3.14×4×4)
C. 9.42×3÷(3.14×4×4) D. 9.42×9÷(3.14×4×4)
一.单选题
B
【解析】【解答】 把一个体积为9.42立方分米的圆锥放入底面半径为4分米的圆柱形装水容器中(水浸没且无溢出),水面上升了多少分米,列式正确的是: 9.42÷(3.14×4×4) 。
故答案为:B。
【分析】根据题意可知,先求出圆柱的底面积,然后用圆柱的体积÷圆柱的底面积=上升水面的高度,据此列式解答。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
9.一个圆的直径扩大3倍,那么它的面积扩大( )倍.
A. 3 B. 6 C. 9 D. 4
一.单选题
C
【解析】【解答】解:假设这个圆原来的直径是2厘米,则扩大后是6厘米.
原来圆的面积 S=πr2=3.14×(2÷2)2=3.14(平方厘米)
扩大后圆的面积 S=πr2=3.14×(6÷2)2=28.26(平方厘米)
28.26÷3.14=9
故选:C.
【分析】这道题中圆的直径没有具体说明是几,如果单纯的去算不好算,因此可以采用“假设法”,也就是举例子,在这里我把原来的直径看做2,则扩大后的直径就是(2×3),再根据圆的面积公式分别算出它们的面积,最后用除法算出答案即可.
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
10.下面的说法错误的有( )句。
①圆柱的底面积与高都扩大3倍,它的体积就扩大6倍。
②既是2的倍数又是5的倍数的数的特征是个位必须是0。
③一条线段绕着它的一个端点旋转120°,形成的图形是圆。
④在长方体上,我们找不到两条既不平行也不相交的线段。
⑤公式S梯=(a+b)h÷2,当a=b时,就是平行四边形的面积计算公式。
A. 1 B. 2 C. 3 D. 4
一.单选题
B
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
一.单选题
【解析】【解答】解:①圆柱的底面积与高都扩大3倍,它的体积就扩大9倍;原来说法错误;
②既是2的倍数又是5的倍数的数的特征是个位必须是0。原来说法正确;
③120÷360=1/3 , 原来说法正确;
④在长方体上,例如前面长方形下面的长与后面长方形的宽就不平行也不相交。原来说法错误;
⑤a=b时,说明上底和下底相等,那么这个图形实际就是一个平行四边形,就是平行四边形的面积计算公式。原来说法正确。
故答案为:B。
【分析】①圆柱的体积=底面积×高,因此体积扩大的倍数是3×3=9;
④长方体相对面不对应的长和宽既不平行也不相交。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
11.从圆锥的顶点到底面圆周上任意一点的距离是圆锥的高。( )
二.判断题
错误
【解析】【解答】解:从圆锥的顶点到底面圆心的距离是圆锥的高。原题说法错误。
故答案为:错误。
【分析】圆锥只有一条高,是圆锥顶点到底面圆心的距离。
12.从圆锥的顶点到底面周长任意一点的连线都是圆锥的高.( )
【解答】 从圆锥的顶点到底面圆心的距离是圆锥的高,原题说法错误.
故答案为:错误.
【分析】 根据圆锥体的高的定义可知:从圆锥顶点到底面圆中心的距离叫做圆锥的高,据此判断.
错误
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
13.一个正方体和一个圆柱体的底面积和高都相等,它们的体积也一定相等.
( )
二.判断题
【解析】【解答】解:一个正方体和一个圆柱体的底面积和高都相等,它们的体积也一定相等。原题说法正确。故答案为:正确。
【分析】正方体体积=底面积×高,圆柱体体积=底面积×高,所以底面积和高都相等的正方体和圆柱体的体积相等。
14.圆柱的侧面展开图可能是正方形。( )
【解析】【解答】解:圆柱的侧面展开图可能是正方形,原题说法正确.
故答案为:正确
【分析】圆柱的侧面展开后是一个长方形或正方形,长方形或正方形的一条边与底面周长相等,另一条边与高相等;当底面周长和高相等时侧面展开就是一个正方形.
正确
正确
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
15.圆锥体的体积是8立方厘米,高是2厘米,底面积是12平方厘米。( )
二.判断题
【解析】【解答】解:8×3÷2=12(平方厘米);
故答案为:正确。
【分析】根据圆锥体的体积公式V=1/3 S底h,可以推导出底面积S=3V÷h,据此代入数据解答即可。
正确
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
16.一个圆柱的侧面展开图是一个正方形,高是25.12 cm,这个圆柱的底面半径是______cm。
三.填空题
4
【解析】【解答】解:由题可知,底面周长=25.12厘米,故底面半径=25.12÷2÷π=25.12÷2÷3.14=4(厘米)。
故答案为:4。
【分析】圆柱侧面展开图是一个以底面圆的周长为一边、高为另一边的一个长方形,若为正方形说明底面周长=高。圆的周长C=2πr。π在计算时一般取3.14。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
17.一个圆锥有________条高,一个圆柱有________条高。
A.一 B.二 C.三 D.无数条
三.填空题
A
【解析】【解答】解:一个圆锥有1条高,一个圆柱有无数条高。
故答案为:A;D。
【分析】圆锥顶点到底面圆心的距离就是圆锥的高,圆锥只有一条高;圆柱两个底面之间的距离就是圆柱的高,圆柱有无数条高。
D
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
18.圆锥的侧面展开图是一个________,将圆锥沿高展开,所得到的横截面是一个______________.
三.填空题
扇形
等腰三角形
【解析】【解答】 圆锥的侧面展开图是一个扇形,将圆锥沿高展开,所得到的横截面是一个等腰三角形.
故答案为:扇形;等腰三角形.
【分析】根据对圆锥的认识可知,圆锥的侧面展开图是一个扇形,将圆锥沿高展开,所得到的横截面是一个等腰三角形.
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
19.圆柱的体积不变,如果底面半径扩大到原来的2倍,那么高应该________.
三.填空题
缩小4倍
【解析】【解答】 圆柱的体积不变,如果底面半径扩大到原来的2倍,那么高应该缩小4倍.
故答案为:缩小4倍.
【分析】根据圆柱的体积公式:V=πr2h,当一个圆柱的体积不变,如果底面半径扩大到原来的a倍,那么高应该缩小a2倍,据此解答.
20.将一个圆柱体的高截短3厘米,此时它的表面积会减少18.84平方厘米,那么它的体积会减少________立方厘米。
【解析】【解答】解:18.84÷3=6.28平方厘米,6.28÷3.14÷2=1厘米,12×3.14×3=9.42立方厘米,所以它的体积会减少9.42立方厘米。故答案为:9.42。
【分析】圆柱体只是把高截短了,底面周长不变,所以圆柱体的底面周长=圆柱体减少的表面积÷圆柱体截短的高,圆柱体的底面半径=圆柱体的底面周长÷π÷2,所以圆柱体减少的体积=πr2×截短的高。
9.42
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
21.想一想,填一填。
一个圆柱的体积是6m3,和它等底等高的圆锥的体积是________ m3 。
三.填空题
2
22.一根长1米的圆木,现将它锯成同样长短的两段,表面积增加了56平方厘米,这根圆木原来的体积是________立方厘米.
【解析】【解答】1米=100厘米;
56÷2=28(平方厘米);
28×100=2800(立方厘米).
故答案为:2800.
【分析】根据1米=100厘米,先将单位化统一,将一根圆木锯成同样长短的两段,表面积增加了2个底面积,用增加的表面积÷2=圆柱的底面积,然后用圆柱的底面积×高=圆柱的体积,据此列式解答.
2800
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
【解析】【解答】6× =2(立方米)
【分析】等底等高的圆锥的体积是圆柱的体积的 ,所以可用圆柱的体积乘 即可得到圆锥的体积。
23.一个圆柱削去2.4立方米后,正好削成一个与它等底等高的圆锥,削成的这个圆锥的体积是________立方米,圆柱原来的体积是________立方米。
三.填空题
1.2
【解析】【解答】圆锥的体积:2.4÷2=1.2(立方米);
圆柱的体积:1.2×3=3.6(立方米).
故答案为:1.2;3.6 。
【分析】根据题意可知,将一个圆柱削成一个等底等高的圆锥,削去部分的体积是圆锥体积的2倍,据此用削去部分的体积÷2=圆锥的体积,等底等高的圆柱体积是圆锥体积的3倍,用圆锥的体积×3=圆柱的体积,据此列式解答.
3.6
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
24.圆锥有________条高,是________和____________的连线。
三.填空题
1
【解答】1;顶点;底面圆心
顶点
底面圆心
25.等底等高的圆柱和圆锥,它们的体积一共是60立方米,那么圆锥体积是________立方米。
【解析】【解答】等底等高的圆柱和圆锥,它们的体积比是3:1,所以圆锥的体积是总体积的,所以圆锥的体积是60×=15
15
【分析】等底等高的圆柱和圆锥,它们的体积比是3:1,按照按比例分配解题的方法即可解答。
【解析】根据圆锥特点,辨别圆锥,了解它的组成部分,界定它的组成部分的概念。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
26.李师傅做了50个直经是8dm高是12dm的圆柱形铁桶,每1dm2的铁桶重6.5kg,做好这些铁桶应该用多少千克的铁皮?
四.解答题
【答案】 解:底面积:3.14×(8÷2)2
=3.14×16
=50.24(平方分米)
侧面积:3.14×8×12
=3.14×96
=301.44(平方分米)
【分析】根据题意可知,先求出每个无盖圆柱形铁桶的表面积,然后用每个无盖铁桶的表面积×制作的铁桶的个数×每立方分米铁桶的质量=一共需要的质量,据此列式解答。
需要铁皮重量:
(50.24+301.44)×50×6.5
=351.68×325
=114296(千克)
答:做好这些铁桶应该用114296千克的铁皮。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
27.一个酒瓶里面深30cm,底面内直径是10cm,瓶里酒深15cm。把瓶口塞紧后使其瓶口向下倒立,这时酒深25cm。求酒瓶的容积。
四.解答题
【答案】 解:3.14×(10÷2)2×[15+(30-25)]=1570(cm3)
答:酒瓶的容积是1570 cm3。
【分析】酒瓶的容积相当于高15厘米的圆柱形酒的体积,和高是(30-25)厘米的圆柱形空气的体积,把这两部分体积相加就是酒瓶的容积。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
28.一个圆锥形沙滩,底面周长是21.98m,高1.2m。如果每立方米沙重1.5t,这堆沙重多少吨
四.解答题
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
【答案】解:3.14×(21.98 ÷6.28) ×1.2× ×1.5
=15.386×1.5
=23.079(吨)
答:这堆沙重23.079吨
【分析】圆锥的体积= ×底面积×高。高已知,根据底面周长求出半径,根据半径求出底面积;沙重=圆锥体积×1.5吨,据此可求解。
29.小组同学在一起找一个圆锥形的物体(一堆沙子等),想办法计算出它的体积.
四.解答题
【答案】解:可以测量出圆锥的底面周长和高,用底面周长除以3.14,再除以2求出底面半径,然后用底面积乘高乘即可求出推体积.
【解析】【分析】测量底面的半径有难度,可以通过测量底面周长来计算出底面半径,再测量出高;然后根据公式计算,圆锥的体积=底面积×高×1/3.
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
30.学校绘画组一共有48人,如果每组6人,可以分成多少组?如果要平均分成4组,每组有多少人?
四.解答题
【答案】 解:48÷6=8(组)
48÷4=12(人)
答:如果每组6人,可以分成8组,如果要平均分成4组,每组有12人。
【解析】【分析】如果每组6人,可以分成的组数=绘画组的总人数÷6;如果平均分成4组,每组的人数=绘画组的总人数÷4。据此代入数据作答即可。
人教版六年级数学下册第三章《圆柱与圆锥》考前押题卷(第三套)
谢谢您的观看!
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
