人教版九下:29.1 投影 教案(3课时,表格式)
文档属性
| 名称 | 人教版九下:29.1 投影 教案(3课时,表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 523.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-08 16:02:12 | ||
图片预览



文档简介
课题: 投影
教学目标:
1、经历实践探索,了解投影、平行投影、中心投影、正投影的概念;
2、能根据正投影的性质画出简单的平面图形的正投影。
3、使学生学会关注生活中有关投影的数学问题,提高数学的应用意识。
教学重点:投影、平行投影、中心投影、正投影的概念。
教学难点:根据正投影的性质画出简单的平面图形的正投影。
导学流程及学习内容
方法指导或行为提示
目标导学
【创设情境】
你看过皮影戏吗? 皮影戏又名“灯影子”,是我国民间一种古老而奇特的戏曲艺术,在关中地区很为流行。北京故宫中的日晷闻名世界,是我国光辉出灿烂文化的瑰宝.它是我国古代利用日影测定时刻的仪器,它由“晷面”与“晷针”组成,当太阳光照在日晷中轴上产生投影,晷针的影子就会投向晷面,随着时间的推移,晷针的影的长度发生变化,晷针的影子在晷面上慢慢移动,聪明的古人以此来显示时刻.
问题:那什么是投影呢?
揭示课题,明确目标。
二、新知探究
(一)自学自研
探究一:投影
1.光线照射物体,会在平面上(如地面、墙壁)留下它的影子,把物体映成它的影子叫作________.照射的光线叫____________,投影所在的平面叫____________.物体在投影下的像简称为物体的________.
探究二:平行投影、中心投影
由________光线形成的投影叫做平行投影,由________发出的光线形成的影子就是中心投影.
3.平行投影与中心投影的区别与联系
区别
联系
光线
物体与投影面平行时的投影
平行投影
平行的投射线
全等
都是物体在光线的照射下,在某个平面内形成的影子。(即都是投影)
中心投影
从一点出发的投射线
放大(位似变换)
探究三:正投影
5.在平行投影中,如果投影线与投影面互相垂直,就称为________。
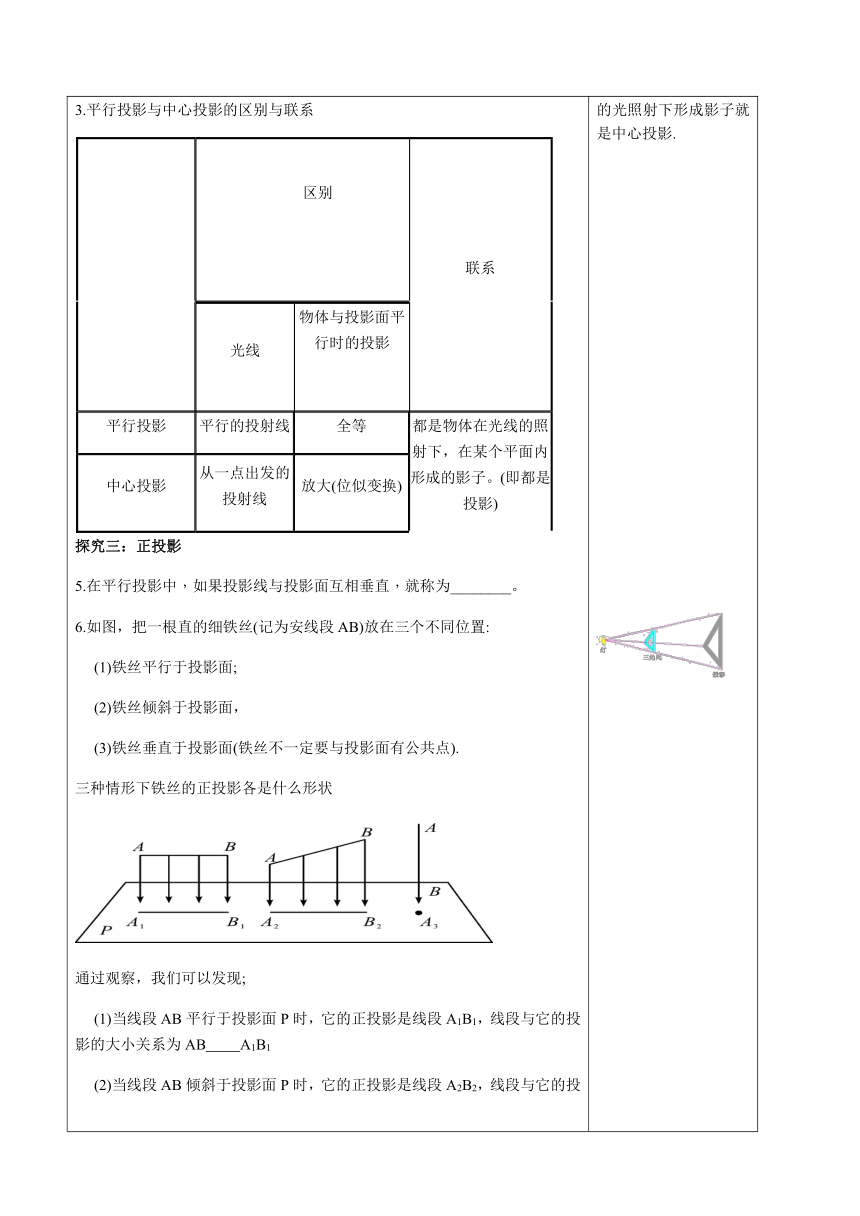
6.如图,把一根直的细铁丝(记为安线段AB)放在三个不同位置:
??? (1)铁丝平行于投影面;
??? (2)铁丝倾斜于投影面,
??? (3)铁丝垂直于投影面(铁丝不一定要与投影面有公共点).
三种情形下铁丝的正投影各是什么形状?
通过观察,我们可以发现;
??? (1)当线段AB平行于投影面P时,它的正投影是线段A1B1,线段与它的投影的大小关系为AB ? ????A1B1??
??? (2)当线段AB倾斜于投影面P时,它的正投影是线段A2B2,线段与它的投影的大小关系为AB ?? ???A2B2
?? ?(3)当线段AB垂直于投影面P时,它的正投影是一个点A3
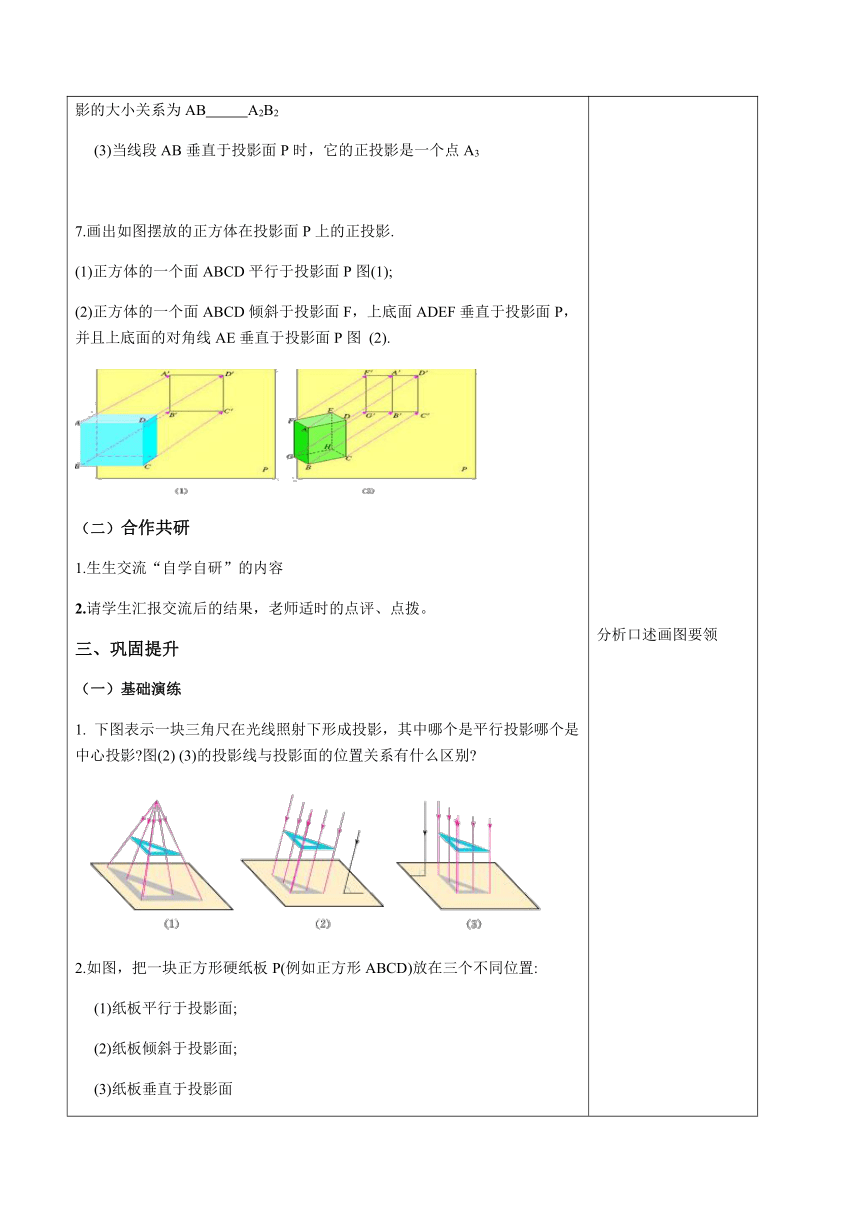
7.画出如图摆放的正方体在投影面P上的正投影.
(1)正方体的一个面ABCD平行于投影面P图(1);
(2)正方体的一个面ABCD倾斜于投影面F,上底面ADEF垂直于投影面P,并且上底面的对角线AE垂直于投影面P图 (2).
合作共研
生生交流“自学自研”的内容
请学生汇报交流后的结果,老师适时的点评、点拨。
三、巩固提升
(一)基础演练
下图表示一块三角尺在光线照射下形成投影,其中哪个是平行投影哪个是中心投影?图(2) (3)的投影线与投影面的位置关系有什么区别?
2.如图,把一块正方形硬纸板P(例如正方形ABCD)放在三个不同位置:
??? (1)纸板平行于投影面;
??? (2)纸板倾斜于投影面;
??? (3)纸板垂直于投影面
结论:
(1)当纸板P平行于投影面Q时. P的正投影与P的形状、大小一样;
(2)当纸板P倾斜于投影面Q时. P的正投影与P的形状、大小发生变化;
(3)当纸板P垂直于投影面Q时. P的正投影成为一条线段.
当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同.
(二)变式提高
3.确定下图中路灯灯泡所在的位置.
(三)拓展延伸
课本第98页练习1、2、3
四、学后反思
以”本节课我们学到了什么?”启发学生谈谈本节课的收获.
五、课后达标(课外作业)
见《课堂内外》
例如.物体在太阳光的照射下形成的影子(简称日影)就是平行投影.
例如.物体在灯泡发出的光照射下形成影子就是中心投影.
419104539615
分析口述画图要领
教后反思:
九年级 数学 新授课 第3章 第2课时 总第_______课时 主备人
课题: 3.2 直棱柱、圆锥的侧面展开图
教学目标:
1、了解直棱柱、圆锥的侧面展开图的概念.
2、会在简单情况下判断一个平面图形是不是直棱柱的表面展开图,培养学生的空间想象能力.
3、能根据展开图判断和制作立体模型.
教学重点:会认和画直棱柱的表面展开图.。
教学难点:立方体的表面展开图的辨认。
导学流程及学习内容
方法指导或行为提示
一、目标导学
【创设情境】
2211070683895A
B
A
B
在一个长方形长、宽、高 分别为3米,2米,2米长方体房间内,一蜘蛛在一面的中间,离天花板0.1米处(A点),苍蝇在对面墙的中间,离地面0.1米处(B点),试问:蜘蛛去捉苍蝇需要爬行的最短距离是多少?
(二)揭示课题,明确目标。
二、新知探究
(一)自学自研
探究一:直棱柱及侧面展开图
直棱柱的棱是指: 。
将直棱柱的侧面沿着一条侧棱剪开,可以展开成平面图形,像这样的平面图形称为直棱柱的____________.直棱柱的侧面展开图是一个________,这个矩形的长是直棱柱的________,宽是直棱柱的________.
直棱柱将立方体沿某些棱剪开后铺平,且六个面连在一起,这样的图形叫立方体的表面展开图.
它具有以下特征:
(1) 。
(2) 。
(3) 。
正棱柱是: 。
1.连连看:(用线连接各立方体的表面展开图)
224536020955937895317505143590805
3520440176530195262546990
1238885501652984538735
25507956351
5
4
6
3
2
a
h
b
b
b
b
a
a
1
5
6
3
2
4
1
5
4
6
3
2
a
h
b
b
b
b
a
a
1
5
6
3
2
4
2.求出包装盒的侧面积和表面积
探究二:圆锥及侧面展开图
圆锥是由一个底面和一个侧面围成的图形,它的底面是一个________.连接顶点与底面圆心的线段叫作圆锥的________.圆锥顶点与底面圆上任意一点的线段都叫作圆锥的________,母线的长度均________.
把圆锥沿它的一条母线剪开,它的侧面可以展开成平面图形,像这样的平面图形称为圆锥的____________________.圆锥的侧面展开图是一个________,这个扇形的半径是圆锥的____________,弧长是圆锥底面圆的________.
3.把一个用来盛爆米花的圆锥形纸杯沿母线剪开,可得一个半径为24cm,圆心角为120°的扇形.求该纸杯的底面半径和高度(结果精确到0.1cm)
3267075170815
.
31750003848104.圆锥形的烟囱帽的底面直径是80cm, 母线长50cm. (1)画出它的展开图(2)计算这个展开图的圆心角及面积.
(二)合作共研
1.生生交流“自学自研”的内容
2.请学生汇报交流后的结果,老师适时的点评、点拨。
三、巩固提升
4443730-193040A
C
B
A
C
B
(一)基础演练
1. 如图,有一边长4米立方体形的房间,一只蜘蛛在A处,一只苍蝇在B处。⑴试问,蜘蛛去抓苍蝇需要爬行的最短路程是多少?
⑵若苍蝇在C处,则最短路程是多少?
(二)变式提高
2843530358775A
C
A
C
2.如图,有一长方体形的房间,地面为边长4米的正方形,房间高3米。一只蜘蛛在A处,一只苍蝇在C处。
试问,蜘蛛去抓苍蝇需要爬行的最短路程是多少?
(三)拓展延伸
3.已知:Rt△ABC中,∠C=900,AB=15cm,BC=5cm,
求: △ABC绕AC所在直线旋转一周所得到的几何体的表面积。
四、学后反思
以”本节课我们学到了什么?”启发学生谈谈本节课的收获.
五、课后达标(课外作业)
见《课堂内外》
【设置悬念,并引导学生把三维问题转化为二维来解决】
让学生发挥空间想象,激发学生兴趣,从而导入课题。
思考:
1.直棱柱的侧面展开图是什么图形?
2.如何求直棱柱的侧面展开图面积?
先要观察各立方体的侧面是由哪些平面图形组成。
5407025958850A
C
B
A
C
B
教后反思:
九年级 数学 新授课 第3章 第3课时 总第_______课时 主备人
课题: 3.3 三视图
教学目标:
1.让学生会从投影的角度理解视图的概念
2.会画简单几何体的三视图
3.通过观察探究等活动使学生知道物体的三视图与正投影的相互关系及三视图中位置关系、大小关系。
教学重点:从投影的角度加深对三视图的理解和会画简单的三视图。
教学难点:对三视图概念理解的升华及正确画出三棱柱的三视图。
导学流程及学习内容
方法指导或行为提示
一、目标导学
.这个水平投影能完全反映这个物体的形状和大小吗?如不能,那么还需哪些投影面?
物体的正投影从一个方向反映了物体的形状和大小,为了全面地反映一个物体的形状和大小,我们常常再选择正面和侧面两个投影
2103755106680揭示课题,明确目标。
二、新知探究
(一)自学自研
探究一:三视图的概念及画法
视图的概念: 。
1.长方体三视图的画法:
如图(2),将三个投影面展开在一个平面内,得到这一物体的一张三视图(由主视图,俯视图和左视图组成).三视图中的各视图,分别从不同方面表示物体,三者合起来就
能够较全面地反映物体的形状.
通过以上的学习,你有什么发现?
物体的三视图实际上是物体在三个不同方向的正投影.正投影面上的正投影就是主视图,水平投影面上的
正投影就是俯视图,侧投影面上的
正投影就是左视图
探究二:根据三视图说出立体图形
2.根据下面的三视图说出立体图形的名称.
3286125153035
3.根据物体的三视图(如下图)描述物体的形状.
3590925149860
153352591440
3581400636270?
(二)合作共研
1.生生交流“自学自研”的内容
2.请学生汇报交流后的结果,老师适时的点评、点拨。
三、巩固提升
(一)基础演练
1.画出下图所示的一些基本几何体的三视图.
2.某几何体的三种视图分别如下图所示,那么这个几何体可能是( )。
(A)长方体 (B)圆柱 (C)圆锥 (D)球
(二)变式提高
3.画出正六棱柱的三视图
25190451295404.右图是一根钢管的直观图,画出它的三视图
339090121920
5.如图所示是一个立体图形的三视图,请根据视图说出立体图形的名称_______。
?
(三)拓展延伸
6.一张桌子摆放若干碟子,从三个方向上看,三种视图如下图所示,则这张桌子上共有________个碟子。
四、学后反思
以”本节课我们学到了什么?”启发学生谈谈本节课的收获.
五、课后达标(课外作业)
见《课堂内外》
尽量让学生独立思考后回答
一个物体在三个投影面内同时进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图,在水平面内得到的由上向下观察物体的视图,叫做俯视图;在侧面内得到由左向右观察物体的视图,叫做左视图.
三个视图要放在正确的位置.并且使主视图与俯视图的长对正,主视图与左视图的高平齐.左视图与俯视图的宽相等.
分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形,
图2分析:由主视图可知,物体正面是正五边形,由俯视图可知,由上向下看物体是矩形
的,且有一条棱(中间的实线)可见到。两
条棱(虚线)被遮挡,由左视图知,物体的侧
面是矩形的.且有一条棱〔中间的实线)可
见到,综合各视图可知,物体是五棱柱形状的.
分析:画这些基本几何体的三视图时,要注意从三个方面观察它们.具体画法为:
1.确定主视图的位置,画出主视图;
2.在主视图正下方画出俯视图,注意与主视图“长对正”。
3.在主视图正右方画出左视图.注意与主视图“高平齐”,与俯视图“宽相等”.
教后反思:
教学目标:
1、经历实践探索,了解投影、平行投影、中心投影、正投影的概念;
2、能根据正投影的性质画出简单的平面图形的正投影。
3、使学生学会关注生活中有关投影的数学问题,提高数学的应用意识。
教学重点:投影、平行投影、中心投影、正投影的概念。
教学难点:根据正投影的性质画出简单的平面图形的正投影。
导学流程及学习内容
方法指导或行为提示
目标导学
【创设情境】
你看过皮影戏吗? 皮影戏又名“灯影子”,是我国民间一种古老而奇特的戏曲艺术,在关中地区很为流行。北京故宫中的日晷闻名世界,是我国光辉出灿烂文化的瑰宝.它是我国古代利用日影测定时刻的仪器,它由“晷面”与“晷针”组成,当太阳光照在日晷中轴上产生投影,晷针的影子就会投向晷面,随着时间的推移,晷针的影的长度发生变化,晷针的影子在晷面上慢慢移动,聪明的古人以此来显示时刻.
问题:那什么是投影呢?
揭示课题,明确目标。
二、新知探究
(一)自学自研
探究一:投影
1.光线照射物体,会在平面上(如地面、墙壁)留下它的影子,把物体映成它的影子叫作________.照射的光线叫____________,投影所在的平面叫____________.物体在投影下的像简称为物体的________.
探究二:平行投影、中心投影
由________光线形成的投影叫做平行投影,由________发出的光线形成的影子就是中心投影.
3.平行投影与中心投影的区别与联系
区别
联系
光线
物体与投影面平行时的投影
平行投影
平行的投射线
全等
都是物体在光线的照射下,在某个平面内形成的影子。(即都是投影)
中心投影
从一点出发的投射线
放大(位似变换)
探究三:正投影
5.在平行投影中,如果投影线与投影面互相垂直,就称为________。
6.如图,把一根直的细铁丝(记为安线段AB)放在三个不同位置:
??? (1)铁丝平行于投影面;
??? (2)铁丝倾斜于投影面,
??? (3)铁丝垂直于投影面(铁丝不一定要与投影面有公共点).
三种情形下铁丝的正投影各是什么形状?
通过观察,我们可以发现;
??? (1)当线段AB平行于投影面P时,它的正投影是线段A1B1,线段与它的投影的大小关系为AB ? ????A1B1??
??? (2)当线段AB倾斜于投影面P时,它的正投影是线段A2B2,线段与它的投影的大小关系为AB ?? ???A2B2
?? ?(3)当线段AB垂直于投影面P时,它的正投影是一个点A3
7.画出如图摆放的正方体在投影面P上的正投影.
(1)正方体的一个面ABCD平行于投影面P图(1);
(2)正方体的一个面ABCD倾斜于投影面F,上底面ADEF垂直于投影面P,并且上底面的对角线AE垂直于投影面P图 (2).
合作共研
生生交流“自学自研”的内容
请学生汇报交流后的结果,老师适时的点评、点拨。
三、巩固提升
(一)基础演练
下图表示一块三角尺在光线照射下形成投影,其中哪个是平行投影哪个是中心投影?图(2) (3)的投影线与投影面的位置关系有什么区别?
2.如图,把一块正方形硬纸板P(例如正方形ABCD)放在三个不同位置:
??? (1)纸板平行于投影面;
??? (2)纸板倾斜于投影面;
??? (3)纸板垂直于投影面
结论:
(1)当纸板P平行于投影面Q时. P的正投影与P的形状、大小一样;
(2)当纸板P倾斜于投影面Q时. P的正投影与P的形状、大小发生变化;
(3)当纸板P垂直于投影面Q时. P的正投影成为一条线段.
当物体的某个面平行于投影面时,这个面的正投影与这个面的形状、大小完全相同.
(二)变式提高
3.确定下图中路灯灯泡所在的位置.
(三)拓展延伸
课本第98页练习1、2、3
四、学后反思
以”本节课我们学到了什么?”启发学生谈谈本节课的收获.
五、课后达标(课外作业)
见《课堂内外》
例如.物体在太阳光的照射下形成的影子(简称日影)就是平行投影.
例如.物体在灯泡发出的光照射下形成影子就是中心投影.
419104539615
分析口述画图要领
教后反思:
九年级 数学 新授课 第3章 第2课时 总第_______课时 主备人
课题: 3.2 直棱柱、圆锥的侧面展开图
教学目标:
1、了解直棱柱、圆锥的侧面展开图的概念.
2、会在简单情况下判断一个平面图形是不是直棱柱的表面展开图,培养学生的空间想象能力.
3、能根据展开图判断和制作立体模型.
教学重点:会认和画直棱柱的表面展开图.。
教学难点:立方体的表面展开图的辨认。
导学流程及学习内容
方法指导或行为提示
一、目标导学
【创设情境】
2211070683895A
B
A
B
在一个长方形长、宽、高 分别为3米,2米,2米长方体房间内,一蜘蛛在一面的中间,离天花板0.1米处(A点),苍蝇在对面墙的中间,离地面0.1米处(B点),试问:蜘蛛去捉苍蝇需要爬行的最短距离是多少?
(二)揭示课题,明确目标。
二、新知探究
(一)自学自研
探究一:直棱柱及侧面展开图
直棱柱的棱是指: 。
将直棱柱的侧面沿着一条侧棱剪开,可以展开成平面图形,像这样的平面图形称为直棱柱的____________.直棱柱的侧面展开图是一个________,这个矩形的长是直棱柱的________,宽是直棱柱的________.
直棱柱将立方体沿某些棱剪开后铺平,且六个面连在一起,这样的图形叫立方体的表面展开图.
它具有以下特征:
(1) 。
(2) 。
(3) 。
正棱柱是: 。
1.连连看:(用线连接各立方体的表面展开图)
224536020955937895317505143590805
3520440176530195262546990
1238885501652984538735
25507956351
5
4
6
3
2
a
h
b
b
b
b
a
a
1
5
6
3
2
4
1
5
4
6
3
2
a
h
b
b
b
b
a
a
1
5
6
3
2
4
2.求出包装盒的侧面积和表面积
探究二:圆锥及侧面展开图
圆锥是由一个底面和一个侧面围成的图形,它的底面是一个________.连接顶点与底面圆心的线段叫作圆锥的________.圆锥顶点与底面圆上任意一点的线段都叫作圆锥的________,母线的长度均________.
把圆锥沿它的一条母线剪开,它的侧面可以展开成平面图形,像这样的平面图形称为圆锥的____________________.圆锥的侧面展开图是一个________,这个扇形的半径是圆锥的____________,弧长是圆锥底面圆的________.
3.把一个用来盛爆米花的圆锥形纸杯沿母线剪开,可得一个半径为24cm,圆心角为120°的扇形.求该纸杯的底面半径和高度(结果精确到0.1cm)
3267075170815
.
31750003848104.圆锥形的烟囱帽的底面直径是80cm, 母线长50cm. (1)画出它的展开图(2)计算这个展开图的圆心角及面积.
(二)合作共研
1.生生交流“自学自研”的内容
2.请学生汇报交流后的结果,老师适时的点评、点拨。
三、巩固提升
4443730-193040A
C
B
A
C
B
(一)基础演练
1. 如图,有一边长4米立方体形的房间,一只蜘蛛在A处,一只苍蝇在B处。⑴试问,蜘蛛去抓苍蝇需要爬行的最短路程是多少?
⑵若苍蝇在C处,则最短路程是多少?
(二)变式提高
2843530358775A
C
A
C
2.如图,有一长方体形的房间,地面为边长4米的正方形,房间高3米。一只蜘蛛在A处,一只苍蝇在C处。
试问,蜘蛛去抓苍蝇需要爬行的最短路程是多少?
(三)拓展延伸
3.已知:Rt△ABC中,∠C=900,AB=15cm,BC=5cm,
求: △ABC绕AC所在直线旋转一周所得到的几何体的表面积。
四、学后反思
以”本节课我们学到了什么?”启发学生谈谈本节课的收获.
五、课后达标(课外作业)
见《课堂内外》
【设置悬念,并引导学生把三维问题转化为二维来解决】
让学生发挥空间想象,激发学生兴趣,从而导入课题。
思考:
1.直棱柱的侧面展开图是什么图形?
2.如何求直棱柱的侧面展开图面积?
先要观察各立方体的侧面是由哪些平面图形组成。
5407025958850A
C
B
A
C
B
教后反思:
九年级 数学 新授课 第3章 第3课时 总第_______课时 主备人
课题: 3.3 三视图
教学目标:
1.让学生会从投影的角度理解视图的概念
2.会画简单几何体的三视图
3.通过观察探究等活动使学生知道物体的三视图与正投影的相互关系及三视图中位置关系、大小关系。
教学重点:从投影的角度加深对三视图的理解和会画简单的三视图。
教学难点:对三视图概念理解的升华及正确画出三棱柱的三视图。
导学流程及学习内容
方法指导或行为提示
一、目标导学
.这个水平投影能完全反映这个物体的形状和大小吗?如不能,那么还需哪些投影面?
物体的正投影从一个方向反映了物体的形状和大小,为了全面地反映一个物体的形状和大小,我们常常再选择正面和侧面两个投影
2103755106680揭示课题,明确目标。
二、新知探究
(一)自学自研
探究一:三视图的概念及画法
视图的概念: 。
1.长方体三视图的画法:
如图(2),将三个投影面展开在一个平面内,得到这一物体的一张三视图(由主视图,俯视图和左视图组成).三视图中的各视图,分别从不同方面表示物体,三者合起来就
能够较全面地反映物体的形状.
通过以上的学习,你有什么发现?
物体的三视图实际上是物体在三个不同方向的正投影.正投影面上的正投影就是主视图,水平投影面上的
正投影就是俯视图,侧投影面上的
正投影就是左视图
探究二:根据三视图说出立体图形
2.根据下面的三视图说出立体图形的名称.
3286125153035
3.根据物体的三视图(如下图)描述物体的形状.
3590925149860
153352591440
3581400636270?
(二)合作共研
1.生生交流“自学自研”的内容
2.请学生汇报交流后的结果,老师适时的点评、点拨。
三、巩固提升
(一)基础演练
1.画出下图所示的一些基本几何体的三视图.
2.某几何体的三种视图分别如下图所示,那么这个几何体可能是( )。
(A)长方体 (B)圆柱 (C)圆锥 (D)球
(二)变式提高
3.画出正六棱柱的三视图
25190451295404.右图是一根钢管的直观图,画出它的三视图
339090121920
5.如图所示是一个立体图形的三视图,请根据视图说出立体图形的名称_______。
?
(三)拓展延伸
6.一张桌子摆放若干碟子,从三个方向上看,三种视图如下图所示,则这张桌子上共有________个碟子。
四、学后反思
以”本节课我们学到了什么?”启发学生谈谈本节课的收获.
五、课后达标(课外作业)
见《课堂内外》
尽量让学生独立思考后回答
一个物体在三个投影面内同时进行正投影,在正面内得到的由前向后观察物体的视图,叫做主视图,在水平面内得到的由上向下观察物体的视图,叫做俯视图;在侧面内得到由左向右观察物体的视图,叫做左视图.
三个视图要放在正确的位置.并且使主视图与俯视图的长对正,主视图与左视图的高平齐.左视图与俯视图的宽相等.
分析:由三视图想象立体图形时,要先分别根据主视图、俯视图和左视图想象立体图形的前面、上面和左侧面,然后再综合起来考虑整体图形,
图2分析:由主视图可知,物体正面是正五边形,由俯视图可知,由上向下看物体是矩形
的,且有一条棱(中间的实线)可见到。两
条棱(虚线)被遮挡,由左视图知,物体的侧
面是矩形的.且有一条棱〔中间的实线)可
见到,综合各视图可知,物体是五棱柱形状的.
分析:画这些基本几何体的三视图时,要注意从三个方面观察它们.具体画法为:
1.确定主视图的位置,画出主视图;
2.在主视图正下方画出俯视图,注意与主视图“长对正”。
3.在主视图正右方画出左视图.注意与主视图“高平齐”,与俯视图“宽相等”.
教后反思:
