人教版九下:28.2 解直角三角形的应用 例3和例4 教案
文档属性
| 名称 | 人教版九下:28.2 解直角三角形的应用 例3和例4 教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 270.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-08 16:02:12 | ||
图片预览

文档简介
解直角三角形—应用举例
学习目标
能把实际问题转化为解直角三角形问题,从而会把实际问题转化为数学问题来解决,进一步提高数学建模能力;
通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养学生分析问题、解决问题的能力.
学习重点:
将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识解决实际问题.
学习难点:
画示意图,将实际问题转化为数学模型的建模过程。
教学过程
复习
解直角三角形需要几个要素?
教师出示一个三角形,请同学们添加任意的两个条件来解这个直角三角形
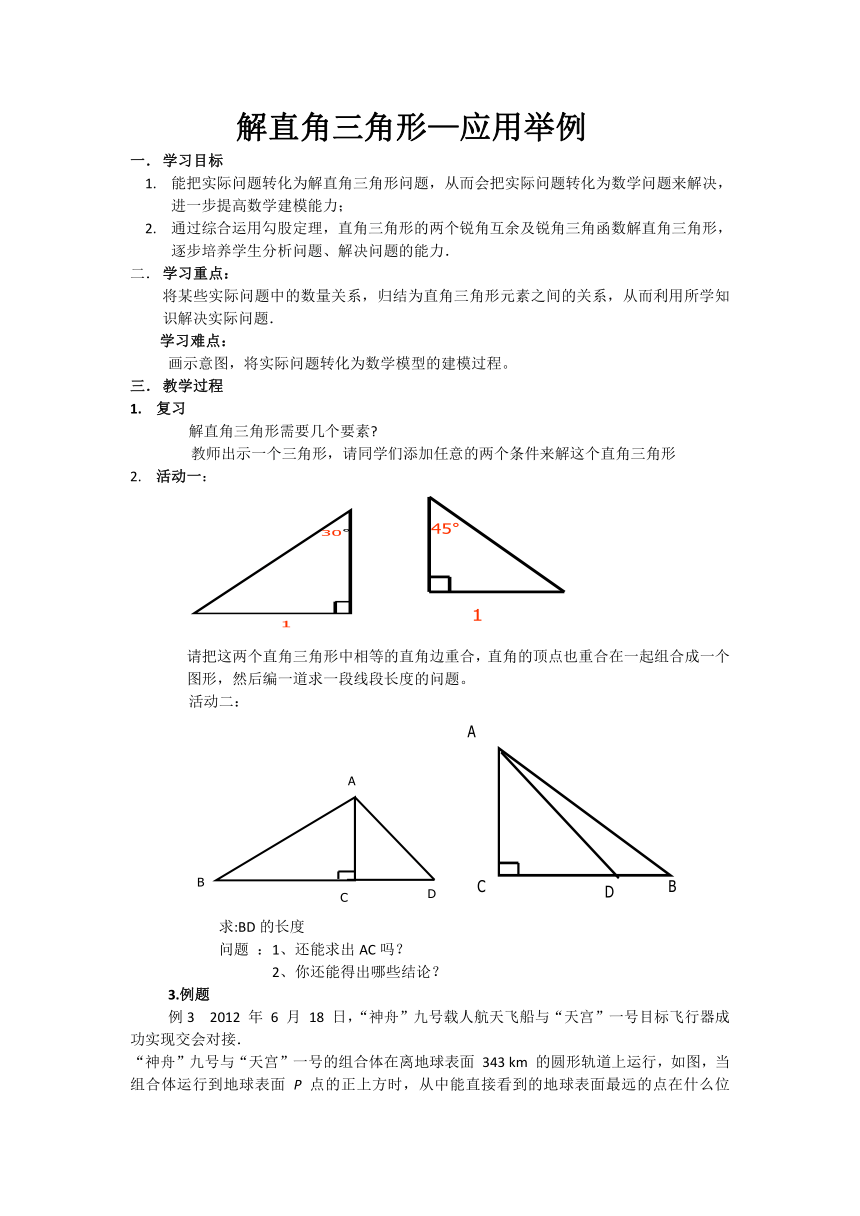
活动一:
30°
1
45°
1
请把这两个直角三角形中相等的直角边重合,直角的顶点也重合在一起组合成一个图形,然后编一道求一段线段长度的问题。
活动二:
A
B
C
D
A
B
C
D
求:BD的长度
问题 :1、还能求出AC吗?
2、你还能得出哪些结论?
3.例题
例3 2012 年 6 月 18 日,“神舟”九号载人航天飞船与“天宫”一号目标飞行器成功实现交会对接.
“神舟”九号与“天宫”一号的组合体在离地球表面 343 km 的圆形轨道上运行,如图,当组合体运行到地球表面 P 点的正上方时,从中能直接看到的地球表面最远的点在什么位置?最远点与 P点的距离是多少(地球半径约为 6 400 km,)
例4. 热气球的探测器显示,从热气球看一栋楼顶部的仰角为 30°,看这栋楼底部的俯角为 60°,热气球与楼的水平距离为 120 m,这栋楼有多高(结果取整数)?
A
B
C
D
α
β
解:过A作AD⊥BC,垂足为D
在Rt△ABD中,因为∠BAD=30°,AD=120m?
所以BD=AD·tan30°=120 = m
在Rt△ACD中
因为∠CAD=60°,AD=120m?
所以CD=AD·tan60°= m
BC=40 +120 =160 ≈ 277.12≈277m
答:这栋楼高为277m。
变式一:热气球的探测器显示,从热气球的底部A处看这栋楼底部C的俯角为60°,看这栋楼M处的俯角为45°,且CM之间的距离为10米,求:热气球A处与高楼的水平距离(结果保留根号)
变式二:
从这栋楼的底部C处看热气球底部A处的仰角为60°,从这栋楼的M处看热气球底部A处的仰角为45°,且CM之间的距离为10米,求:热气球的高度(结果保 留根号)
随堂练习:教材76页1
课堂小结:
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
作业:教材76页2
学习目标
能把实际问题转化为解直角三角形问题,从而会把实际问题转化为数学问题来解决,进一步提高数学建模能力;
通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养学生分析问题、解决问题的能力.
学习重点:
将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识解决实际问题.
学习难点:
画示意图,将实际问题转化为数学模型的建模过程。
教学过程
复习
解直角三角形需要几个要素?
教师出示一个三角形,请同学们添加任意的两个条件来解这个直角三角形
活动一:
30°
1
45°
1
请把这两个直角三角形中相等的直角边重合,直角的顶点也重合在一起组合成一个图形,然后编一道求一段线段长度的问题。
活动二:
A
B
C
D
A
B
C
D
求:BD的长度
问题 :1、还能求出AC吗?
2、你还能得出哪些结论?
3.例题
例3 2012 年 6 月 18 日,“神舟”九号载人航天飞船与“天宫”一号目标飞行器成功实现交会对接.
“神舟”九号与“天宫”一号的组合体在离地球表面 343 km 的圆形轨道上运行,如图,当组合体运行到地球表面 P 点的正上方时,从中能直接看到的地球表面最远的点在什么位置?最远点与 P点的距离是多少(地球半径约为 6 400 km,)
例4. 热气球的探测器显示,从热气球看一栋楼顶部的仰角为 30°,看这栋楼底部的俯角为 60°,热气球与楼的水平距离为 120 m,这栋楼有多高(结果取整数)?
A
B
C
D
α
β
解:过A作AD⊥BC,垂足为D
在Rt△ABD中,因为∠BAD=30°,AD=120m?
所以BD=AD·tan30°=120 = m
在Rt△ACD中
因为∠CAD=60°,AD=120m?
所以CD=AD·tan60°= m
BC=40 +120 =160 ≈ 277.12≈277m
答:这栋楼高为277m。
变式一:热气球的探测器显示,从热气球的底部A处看这栋楼底部C的俯角为60°,看这栋楼M处的俯角为45°,且CM之间的距离为10米,求:热气球A处与高楼的水平距离(结果保留根号)
变式二:
从这栋楼的底部C处看热气球底部A处的仰角为60°,从这栋楼的M处看热气球底部A处的仰角为45°,且CM之间的距离为10米,求:热气球的高度(结果保 留根号)
随堂练习:教材76页1
课堂小结:
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
作业:教材76页2
