人教版九下:28.2 解直角三角形及其应用 教案(表格式)
文档属性
| 名称 | 人教版九下:28.2 解直角三角形及其应用 教案(表格式) | 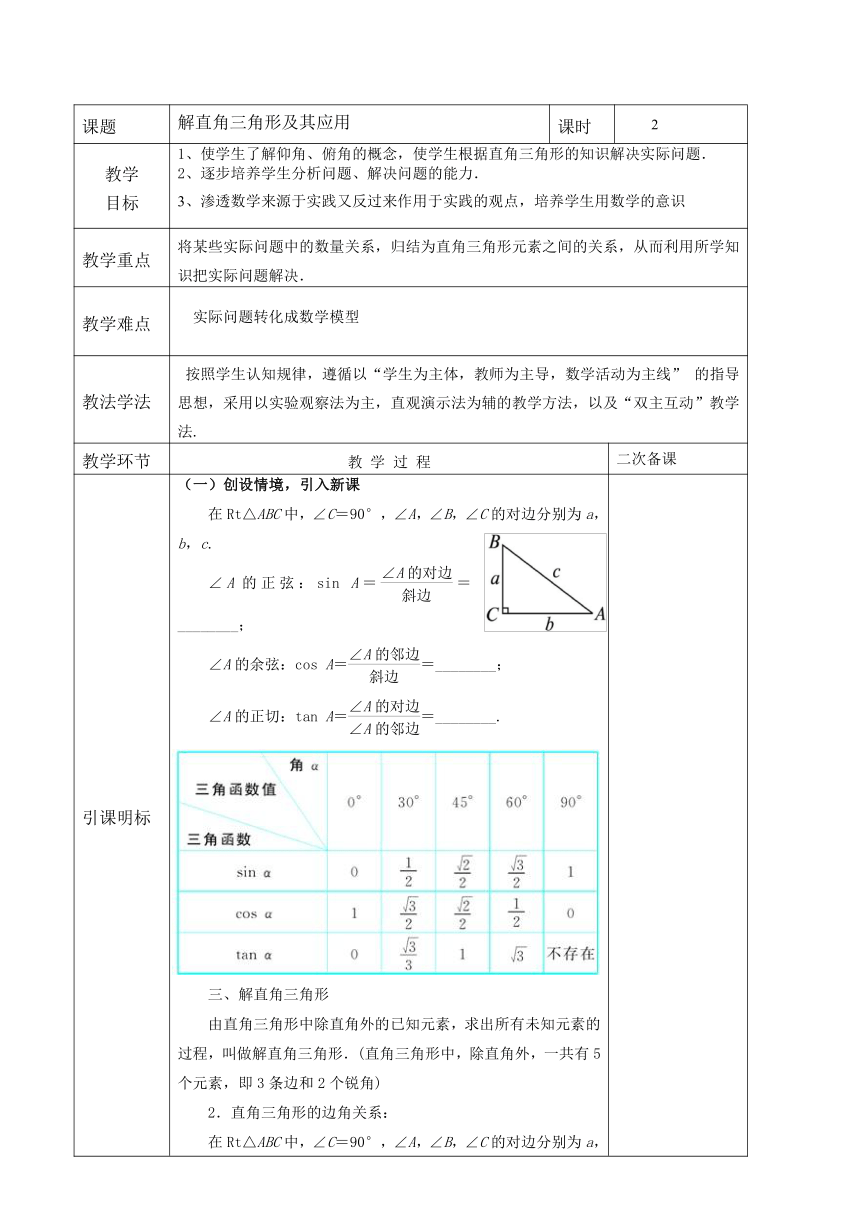 | |
| 格式 | doc | ||
| 文件大小 | 656.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-08 16:02:12 | ||
图片预览


文档简介
课题 解直角三角形及其应用 课时 2
教学 目标 1、使学生了解仰角、俯角的概念,使学生根据直角三角形的知识解决实际问题.
2、逐步培养学生分析问题、解决问题的能力.
3、渗透数学来源于实践又反过来作用于实践的观点,培养学生用数学的意识
教学重点 将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识把实际问题解决.
教学难点
实际问题转化成数学模型
教法学法 按照学生认知规律,遵循以“学生为主体,教师为主导,数学活动为主线” 的指导思想,采用以实验观察法为主,直观演示法为辅的教学方法,以及“双主互动”教学法.
教学环节 教 学 过 程 二次备课
引课明标 (一)创设情境,引入新课
在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.
∠A的正弦:sin A==________;
∠A的余弦:cos A==________;
∠A的正切:tan A==________.
二、特殊角的三角函数值
三、解直角三角形
由直角三角形中除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形.(直角三角形中,除直角外,一共有5个元素,即3条边和2个锐角)
2.直角三角形的边角关系:
在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.
(1)三边之间的关系:____________;
(2)锐角之间的关系:____________;
(二)、展示教学目
自学探究 一、出示提纲,学生自学
认真阅读课本第74至75页的内容,完成下面练习,并体验知识点的形成过程
二、互动学习、质疑解难
例3 2012年6月18日“神舟”九号载人航天飞船发射成功.当飞船完成变轨后,就在离地球表面343km的圆形轨道上运行.如图,当飞船运行到地球表面上P点的正上方时,从飞船上最远能直接看到的地球上的点在什么位置?这样的最远点与P点的距离是多少?(地球半径约为6 400 km, 取3.142,结果精确到0. 1 km)
分析:从飞船上能最远直接看到的地球上最远的点,应是视线与地球相切时的切点
如图,⊙O表示地球,点F是飞船的位置,FQ是⊙O的切线,切点Q是从飞船观测地球时的最远点.弧PQ 的长就是地面上P、Q两点间的距离,为计算弧PQ 的长需先求出∠POQ(即a)
解:在图中,FQ是⊙O的切线,△FOQ是直角三角形
弧PQ的长为
由当飞船在P点正上方时,从飞船观测地球时的最远点距离P点约2009.6km
温馨提示:
仰角、俯角
?当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角.
精讲点拨 例4 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30o,看这栋离楼底部的俯角为60o,热气球与高楼的水平距离为120 m.这栋高楼有多高(结果取整数)?
分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,a=30°,β=60°
Rt△ABC中,a =30°,AD=120,
所以利用解直角三角形的知识求出
BD;类似地可以求出CD,进而求出BC
解:如图,a = 30°,β= 60°, AD=120
.
答:这栋楼高约为277.1m
达标训练
小结提升 当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角.
课后作业
板书设计 §28.2解直角三角形及其应用(2)
教学反思
教学 目标 1、使学生了解仰角、俯角的概念,使学生根据直角三角形的知识解决实际问题.
2、逐步培养学生分析问题、解决问题的能力.
3、渗透数学来源于实践又反过来作用于实践的观点,培养学生用数学的意识
教学重点 将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识把实际问题解决.
教学难点
实际问题转化成数学模型
教法学法 按照学生认知规律,遵循以“学生为主体,教师为主导,数学活动为主线” 的指导思想,采用以实验观察法为主,直观演示法为辅的教学方法,以及“双主互动”教学法.
教学环节 教 学 过 程 二次备课
引课明标 (一)创设情境,引入新课
在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.
∠A的正弦:sin A==________;
∠A的余弦:cos A==________;
∠A的正切:tan A==________.
二、特殊角的三角函数值
三、解直角三角形
由直角三角形中除直角外的已知元素,求出所有未知元素的过程,叫做解直角三角形.(直角三角形中,除直角外,一共有5个元素,即3条边和2个锐角)
2.直角三角形的边角关系:
在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c.
(1)三边之间的关系:____________;
(2)锐角之间的关系:____________;
(二)、展示教学目
自学探究 一、出示提纲,学生自学
认真阅读课本第74至75页的内容,完成下面练习,并体验知识点的形成过程
二、互动学习、质疑解难
例3 2012年6月18日“神舟”九号载人航天飞船发射成功.当飞船完成变轨后,就在离地球表面343km的圆形轨道上运行.如图,当飞船运行到地球表面上P点的正上方时,从飞船上最远能直接看到的地球上的点在什么位置?这样的最远点与P点的距离是多少?(地球半径约为6 400 km, 取3.142,结果精确到0. 1 km)
分析:从飞船上能最远直接看到的地球上最远的点,应是视线与地球相切时的切点
如图,⊙O表示地球,点F是飞船的位置,FQ是⊙O的切线,切点Q是从飞船观测地球时的最远点.弧PQ 的长就是地面上P、Q两点间的距离,为计算弧PQ 的长需先求出∠POQ(即a)
解:在图中,FQ是⊙O的切线,△FOQ是直角三角形
弧PQ的长为
由当飞船在P点正上方时,从飞船观测地球时的最远点距离P点约2009.6km
温馨提示:
仰角、俯角
?当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角.
精讲点拨 例4 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30o,看这栋离楼底部的俯角为60o,热气球与高楼的水平距离为120 m.这栋高楼有多高(结果取整数)?
分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,a=30°,β=60°
Rt△ABC中,a =30°,AD=120,
所以利用解直角三角形的知识求出
BD;类似地可以求出CD,进而求出BC
解:如图,a = 30°,β= 60°, AD=120
.
答:这栋楼高约为277.1m
达标训练
小结提升 当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角.
课后作业
板书设计 §28.2解直角三角形及其应用(2)
教学反思
