人教版九下:28.2.1 解直角三角形 教案
文档属性
| 名称 | 人教版九下:28.2.1 解直角三角形 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 165.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-08 16:02:12 | ||
图片预览

文档简介
课题 解直角三角形
一、教学目标
1.知识与技能:
使学生了解解直角三角形的概念,能运用直角三角形的角与角(两锐角互余),边与边(勾股定理)、边与角关系解直角三角形;
2.过程与方法:
通过学生的探索讨论发现解直角三角形所需的最简条件,使学生了解体会用化归的思想方法将未知问题转化为已知问题去解决;
3.情感态度与价值观:
通过对问题情境的讨论,以及对解直角三角形所需的最简条件的探究,培养学生的问题意识,体验经历运用数学知识解决一些简单的实际问题,渗透“数学建模”的思想。
二、重点难点
1、教学重点:直角三角形的解法。
2、教学难点:(1)三角函数在解直角三角形中的灵活运用。
(2)学生可能不理解在已知的两个元素中,为什么至少有一个是边。
三、教学准备
多媒体(课件),学案,圆规,刻度尺,
四、教学过程
(一)预习检测
阅读教材85-86思考以下问题:
在直角三角形中,除直角外,有几个元素,分别是?
解直角三角形的定义?
在直角三角形中,除直角外的5个元素之间有哪些关系?
知道5个元素中的几个,就可以求其余元素?
1、锐角三角函数的定义:在Rt△ABC中,∠C=90°
sinA= cosA=
tanA=
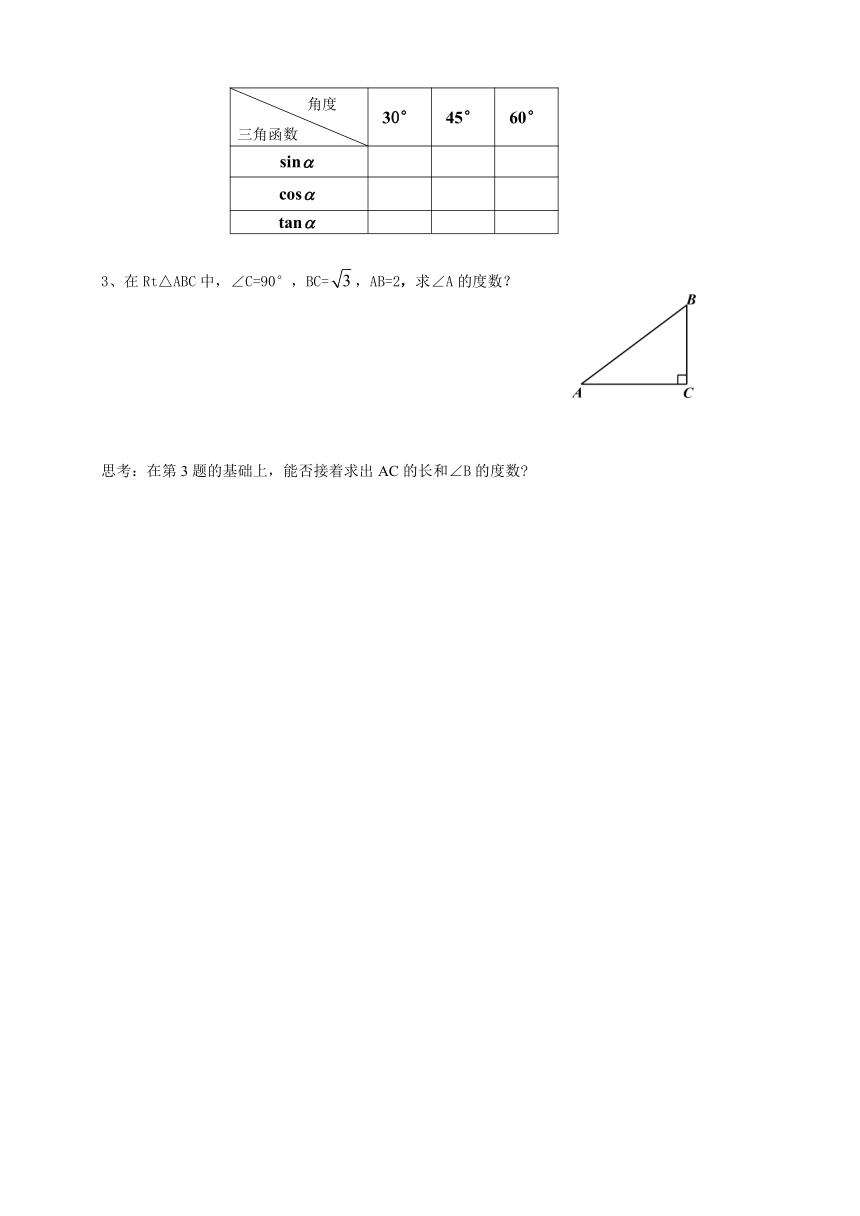
2、特殊角的三角函数值:
30° 45° 60°
sin
cos
tan
3、在Rt△ABC中,∠C=90°,BC=,AB=2,求∠A的度数?
思考:在第3题的基础上,能否接着求出AC的长和∠B的度数?
(二)探究新知
探究一:在直角三角形中,除直角外的5个元素之间有哪些关系?
直角三角形
三边之间的关系
锐角之间关系
边角之间关系
探究二:知道5个元素中的几个,就可以求其余元素?
例题讲解
例1 如图,在Rt△ABC中,∠C=90°,AC= ,BC= ,解在这个直角三角形。
类型:
变式1 如图,在Rt△ABC中,∠C=90°,,,解这个直角三角形。
类型:
变式2 如图,在Rt△ABC中,∠C=90°,∠B=35°,AC=20,解这个直角三角形。(sin 35°0.57,tan 35°0.70,cos 35°0.82,精确到0.1度)
类型:
变式3 如图,在Rt△ABC中,∠C=90°,∠B=35°,AB=20,解这个直角三角形。(sin 35°0.57,tan 35°0.70,cos 35°0.82,精确到0.1)
类型:
练一练
快速说思路:在Rt△ABC中,∠C=90°,根据下列条件解这个直角三角形
(三)巩固提升
1.解直角三角形必须具备的条件是:( )
A.已知一条边 B.已知一条边和一个内角
C.已知一条边和另一个非直角的元素 D.已知两个内角
2. 在Rt△ABC中,,且已知b和的值,那么a的值等于( )
A. B. C. D.
3. 在Rt△ABC中,.,,解这个直角三角形.
4.在Rt△ABC中,已知, 求a、c;
五、自能拓展
例 如图,在Rt△ABC中,∠C=90°,AC=6,∠BAC的平分线,解这个直角三角形。
一、教学目标
1.知识与技能:
使学生了解解直角三角形的概念,能运用直角三角形的角与角(两锐角互余),边与边(勾股定理)、边与角关系解直角三角形;
2.过程与方法:
通过学生的探索讨论发现解直角三角形所需的最简条件,使学生了解体会用化归的思想方法将未知问题转化为已知问题去解决;
3.情感态度与价值观:
通过对问题情境的讨论,以及对解直角三角形所需的最简条件的探究,培养学生的问题意识,体验经历运用数学知识解决一些简单的实际问题,渗透“数学建模”的思想。
二、重点难点
1、教学重点:直角三角形的解法。
2、教学难点:(1)三角函数在解直角三角形中的灵活运用。
(2)学生可能不理解在已知的两个元素中,为什么至少有一个是边。
三、教学准备
多媒体(课件),学案,圆规,刻度尺,
四、教学过程
(一)预习检测
阅读教材85-86思考以下问题:
在直角三角形中,除直角外,有几个元素,分别是?
解直角三角形的定义?
在直角三角形中,除直角外的5个元素之间有哪些关系?
知道5个元素中的几个,就可以求其余元素?
1、锐角三角函数的定义:在Rt△ABC中,∠C=90°
sinA= cosA=
tanA=
2、特殊角的三角函数值:
30° 45° 60°
sin
cos
tan
3、在Rt△ABC中,∠C=90°,BC=,AB=2,求∠A的度数?
思考:在第3题的基础上,能否接着求出AC的长和∠B的度数?
(二)探究新知
探究一:在直角三角形中,除直角外的5个元素之间有哪些关系?
直角三角形
三边之间的关系
锐角之间关系
边角之间关系
探究二:知道5个元素中的几个,就可以求其余元素?
例题讲解
例1 如图,在Rt△ABC中,∠C=90°,AC= ,BC= ,解在这个直角三角形。
类型:
变式1 如图,在Rt△ABC中,∠C=90°,,,解这个直角三角形。
类型:
变式2 如图,在Rt△ABC中,∠C=90°,∠B=35°,AC=20,解这个直角三角形。(sin 35°0.57,tan 35°0.70,cos 35°0.82,精确到0.1度)
类型:
变式3 如图,在Rt△ABC中,∠C=90°,∠B=35°,AB=20,解这个直角三角形。(sin 35°0.57,tan 35°0.70,cos 35°0.82,精确到0.1)
类型:
练一练
快速说思路:在Rt△ABC中,∠C=90°,根据下列条件解这个直角三角形
(三)巩固提升
1.解直角三角形必须具备的条件是:( )
A.已知一条边 B.已知一条边和一个内角
C.已知一条边和另一个非直角的元素 D.已知两个内角
2. 在Rt△ABC中,,且已知b和的值,那么a的值等于( )
A. B. C. D.
3. 在Rt△ABC中,.,,解这个直角三角形.
4.在Rt△ABC中,已知, 求a、c;
五、自能拓展
例 如图,在Rt△ABC中,∠C=90°,AC=6,∠BAC的平分线,解这个直角三角形。
