19.2.2一次函数实际与问题 课件-2020-2021学年人教版八年级数学下册(19张)
文档属性
| 名称 | 19.2.2一次函数实际与问题 课件-2020-2021学年人教版八年级数学下册(19张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 756.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-09 00:00:00 | ||
图片预览




文档简介
空白演示
单击输入您的封面副标题
19.2.2 一次函数与实际 问题
人教版数学八年级下册
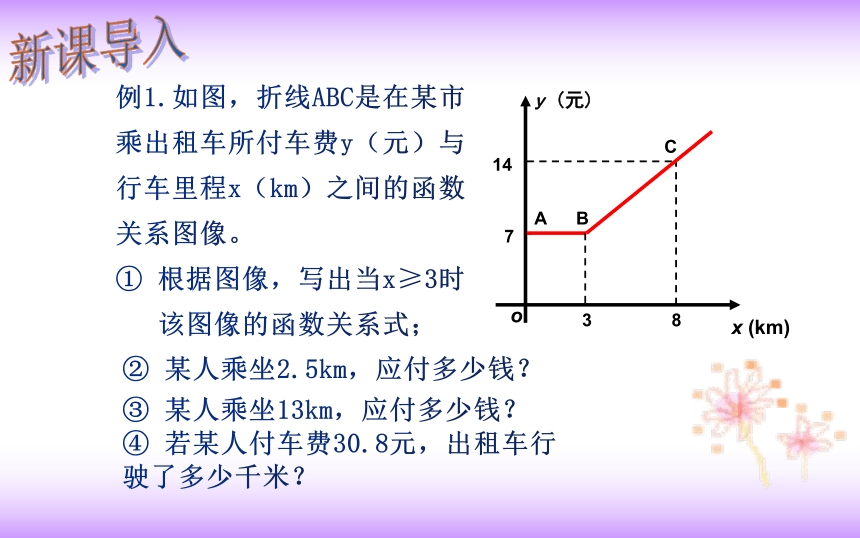
例1.如图,折线ABC是在某市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图像。
① 根据图像,写出当x≥3时
该图像的函数关系式;
y (元)
o
7
14
3
x (km)
8
A
B
C
② 某人乘坐2.5km,应付多少钱?
③ 某人乘坐13km,应付多少钱?
④ 若某人付车费30.8元,出租车行驶了多少千米?
新课导入
解:① 设y=kx+b
把(3,7),(8,14)代入得:
3k+b=7
8k+b=14
解得:
∴
(x≥3)
② ∵2.5<3 由图可知
某人乘坐2.5km,应付7元钱
例题讲解
③把x=13代入
④ 把y=30.8代入
解得x=20
答:若某人付车费30.8元,出租车行驶了20千米。
y=21
答:某人乘坐13km,应付21元钱
例题讲解
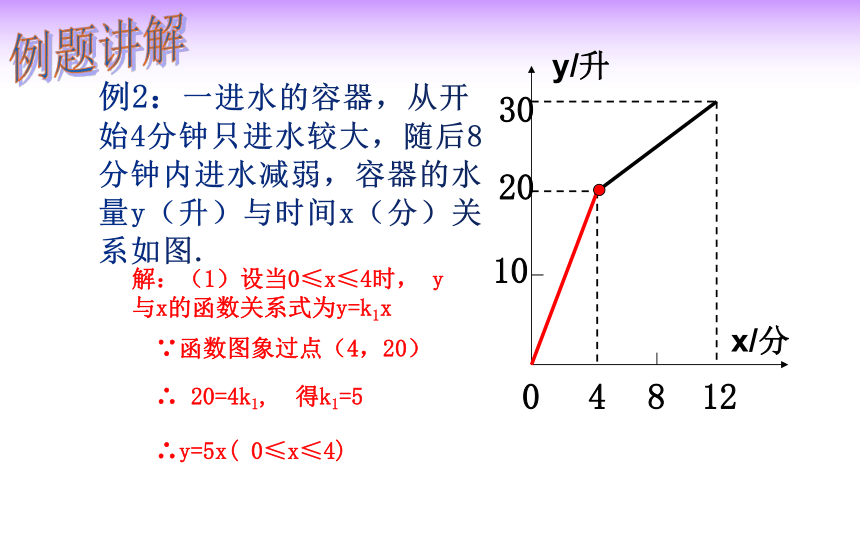
例2:一进水的容器,从开始4分钟只进水较大,随后8分钟内进水减弱,容器的水量y(升)与时间x(分)关系如图。
(1)求当0≤x≤4时,y与x的函数关系式
(2)求当4<x≤12时,y与x的函数关系式
x/分
30
20
10
y/升
0
12
8
4
分析:从函数图象上看图象分为两段,当0≤x≤4时, y与x是正比例函数; 4<x≤12时,y是x的一次函数,且函数图象经过点(4,20)和(12,30),设出相应的函数关系式,将点的坐标代入即可确定函数关系式,根据函数关系式可解决问题.
例题讲解
例2:一进水的容器,从开始4分钟只进水较大,随后8分钟内进水减弱,容器的水量y(升)与时间x(分)关系如图.
y/升
x/分
30
20
10
0
12
8
4
解:(1)设当0≤x≤4时, y与x的函数关系式为y=k1x
∵函数图象过点(4,20)
∴ 20=4k1, 得k1=5
∴y=5x( 0≤x≤4)
例题讲解
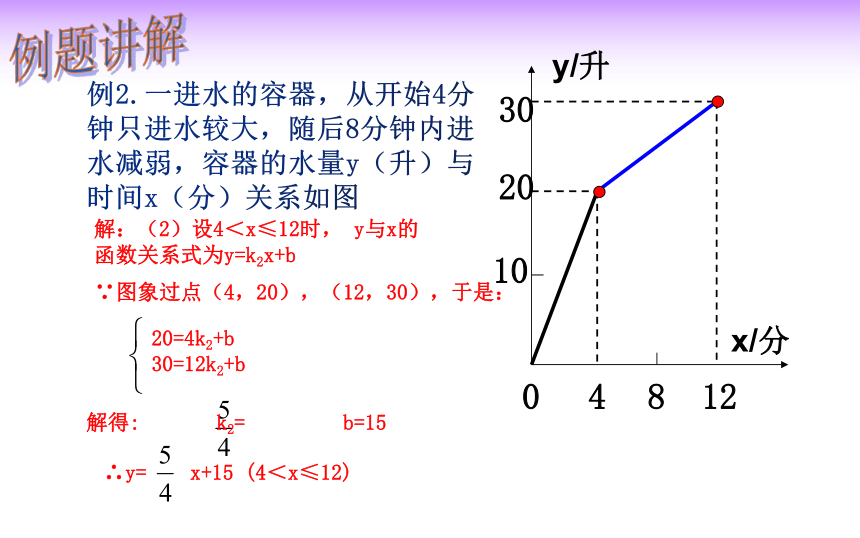
例2.一进水的容器,从开始4分钟只进水较大,随后8分钟内进水减弱,容器的水量y(升)与时间x(分)关系如图
y/升
x/分
30
20
10
0
12
8
4
解:(2)设4<x≤12时, y与x的函数关系式为y=k2x+b
∵图象过点(4,20),(12,30),于是:
20=4k2+b
30=12k2+b
解得: k2= b=15
∴y= x+15 (4<x≤12)
例题讲解
购买种子
数量/kg
0.5
1
1.5
2
2.5
3
3.5
4
…
付款金额/元
…
例3. “黄金1号”玉米种子的价格为5 元/kg,如果一次购买2 kg 以上的种子,超过2 kg 部分的种子的价格打8 折.
(1)填写下表:
2.5
5
7.5
10
12
14
16
18
例题讲解
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
分析:从题目可知,种子的价格与 有关.
若购买种子量为x>2时,种子价格y为:
.
若购买种子量为0≤x≤2时,种子价格y为: .
购买种子量
y=5x
y=4(x-2)+10=4x+2
例题讲解
解:设购买量为x千克,付款金额为y元.
当x>2时,y=4(x-2)+10=4x+2.
当0≤x≤2时,y=5x;
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
叫做分段函数.
注意:1.它是一个函数;
2.要写明自变量取值范围.
y =
5x(0≤x≤2)
4x+2(x>2)
{
y=5x(0≤x≤2)
y=4x+2(x>2)
y
x
O
1
2
10
3
14
例题讲解
思考:
你能由上面的函数解析式或函数图象解决以下问题吗?
(1)一次购买1.5 kg 种子,需付款多少元?
(2)30元最多能购买多少种子?
例题讲解
1、 某工厂月产量y件与月份x(月)的函数图象如图,则下列说法正确的是( )
(A)1月至3月每月产量逐月增加, 4、5两月每月产量逐月减少;
(B)1月至3月每月产量逐月增加, 4、5两月每月产量与3月持平;
(C)1月至3月每月产量逐月增加, 4、5两月均停止生产;
(D)1月至3月每月产量不变, 4、5两月均停止生产.
B
巩固练习
2、图中折线表示超市冷藏室在0:00~4:00的温度m(单位: ℃)随时间t(单位:时)的变化情况:
下列对该冷藏室的温度描述正确的是( )
(A)0:00~2:00温度升高快, 2:00~4:00温度升高慢;
(B)0:00~2:00温度升高慢, 2:00~4:00温度升高快;
(C)0:00~2:00保持6 ℃ 恒温,2:00~4:00保持10 ℃ 恒温;
(D)0:00~2:00保持6 ℃ 恒温,2:00~4:00匀速升温,每小时升高2 ℃ ;
6
10
0
2
4
t
m
D
例题讲解
3、某移动公司采用分段计费的方法来计算话费,月通话时间(分钟)与相应话费(元)之间的函数图象如图所示:
(1)月通话为100分钟时,应交话费 元;
(2)当x>100时,求y与x之间的函数关系式;
(3)月通话为280分钟时,应交话费多少元?
解:(1)观察图象可知月通话为100分钟时,应交话费40元;
(2) 设x>100时, y与x之间的函数关系式为y=kx+b
由图可知:x=100时,y=40;x=200时y=60
则有 , 解之得:
所求函数关系式为:
(3)把x=280代入关系式 得:y=76 即
月通话为280分钟时,应交话费76元.
例题讲解
4.为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(1)求出y关于x的函数解析式;
解:y关于x的函数解析式为:
(1+0.3)x =1.3x, (0≤x≤8)
(1.5+1.2)(x-8)+1.3×8=2.7x-11.2. (x>8)
y=
例题讲解
(2)当x=10时,y=2.7×10-11.2=15.8.
(3)∵1.3×8=10.4<26.6,∴该用户用水量超过8立方米.
∴2.7x-11.2=26.6,解得x=14.
答:应缴水费为15.8元.
答:该户这月用水量为14立方米.
(2)该市一户某月若用水x=10立方米时,求应缴水费;
(3)该市一户某月缴水费26.6元,求该户这月用水量.
例题讲解
1.画分段函数图象的步骤:
①明确函数解析式分几段,以及对应的自变量取值范围是什么,解析式分别是什么;
②选取每一段自变量取值范围端点数值(或特殊值),分别代入对应的解析式计算对应的函数值,得到点的坐标;
③描点;④连线。
2.分段函数中函数自变量的取值范围不同,所对应的函数关系(图象)也不相同。
实际问题
数学问题
数学问题的解
建立函数模型
解函数问题
课堂小结
布置作业
教科书99页,习 题19.2 9, 11题
教科书第60页第3、6题
布置作业
再见
单击输入您的封面副标题
19.2.2 一次函数与实际 问题
人教版数学八年级下册
例1.如图,折线ABC是在某市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图像。
① 根据图像,写出当x≥3时
该图像的函数关系式;
y (元)
o
7
14
3
x (km)
8
A
B
C
② 某人乘坐2.5km,应付多少钱?
③ 某人乘坐13km,应付多少钱?
④ 若某人付车费30.8元,出租车行驶了多少千米?
新课导入
解:① 设y=kx+b
把(3,7),(8,14)代入得:
3k+b=7
8k+b=14
解得:
∴
(x≥3)
② ∵2.5<3 由图可知
某人乘坐2.5km,应付7元钱
例题讲解
③把x=13代入
④ 把y=30.8代入
解得x=20
答:若某人付车费30.8元,出租车行驶了20千米。
y=21
答:某人乘坐13km,应付21元钱
例题讲解
例2:一进水的容器,从开始4分钟只进水较大,随后8分钟内进水减弱,容器的水量y(升)与时间x(分)关系如图。
(1)求当0≤x≤4时,y与x的函数关系式
(2)求当4<x≤12时,y与x的函数关系式
x/分
30
20
10
y/升
0
12
8
4
分析:从函数图象上看图象分为两段,当0≤x≤4时, y与x是正比例函数; 4<x≤12时,y是x的一次函数,且函数图象经过点(4,20)和(12,30),设出相应的函数关系式,将点的坐标代入即可确定函数关系式,根据函数关系式可解决问题.
例题讲解
例2:一进水的容器,从开始4分钟只进水较大,随后8分钟内进水减弱,容器的水量y(升)与时间x(分)关系如图.
y/升
x/分
30
20
10
0
12
8
4
解:(1)设当0≤x≤4时, y与x的函数关系式为y=k1x
∵函数图象过点(4,20)
∴ 20=4k1, 得k1=5
∴y=5x( 0≤x≤4)
例题讲解
例2.一进水的容器,从开始4分钟只进水较大,随后8分钟内进水减弱,容器的水量y(升)与时间x(分)关系如图
y/升
x/分
30
20
10
0
12
8
4
解:(2)设4<x≤12时, y与x的函数关系式为y=k2x+b
∵图象过点(4,20),(12,30),于是:
20=4k2+b
30=12k2+b
解得: k2= b=15
∴y= x+15 (4<x≤12)
例题讲解
购买种子
数量/kg
0.5
1
1.5
2
2.5
3
3.5
4
…
付款金额/元
…
例3. “黄金1号”玉米种子的价格为5 元/kg,如果一次购买2 kg 以上的种子,超过2 kg 部分的种子的价格打8 折.
(1)填写下表:
2.5
5
7.5
10
12
14
16
18
例题讲解
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
分析:从题目可知,种子的价格与 有关.
若购买种子量为x>2时,种子价格y为:
.
若购买种子量为0≤x≤2时,种子价格y为: .
购买种子量
y=5x
y=4(x-2)+10=4x+2
例题讲解
解:设购买量为x千克,付款金额为y元.
当x>2时,y=4(x-2)+10=4x+2.
当0≤x≤2时,y=5x;
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
叫做分段函数.
注意:1.它是一个函数;
2.要写明自变量取值范围.
y =
5x(0≤x≤2)
4x+2(x>2)
{
y=5x(0≤x≤2)
y=4x+2(x>2)
y
x
O
1
2
10
3
14
例题讲解
思考:
你能由上面的函数解析式或函数图象解决以下问题吗?
(1)一次购买1.5 kg 种子,需付款多少元?
(2)30元最多能购买多少种子?
例题讲解
1、 某工厂月产量y件与月份x(月)的函数图象如图,则下列说法正确的是( )
(A)1月至3月每月产量逐月增加, 4、5两月每月产量逐月减少;
(B)1月至3月每月产量逐月增加, 4、5两月每月产量与3月持平;
(C)1月至3月每月产量逐月增加, 4、5两月均停止生产;
(D)1月至3月每月产量不变, 4、5两月均停止生产.
B
巩固练习
2、图中折线表示超市冷藏室在0:00~4:00的温度m(单位: ℃)随时间t(单位:时)的变化情况:
下列对该冷藏室的温度描述正确的是( )
(A)0:00~2:00温度升高快, 2:00~4:00温度升高慢;
(B)0:00~2:00温度升高慢, 2:00~4:00温度升高快;
(C)0:00~2:00保持6 ℃ 恒温,2:00~4:00保持10 ℃ 恒温;
(D)0:00~2:00保持6 ℃ 恒温,2:00~4:00匀速升温,每小时升高2 ℃ ;
6
10
0
2
4
t
m
D
例题讲解
3、某移动公司采用分段计费的方法来计算话费,月通话时间(分钟)与相应话费(元)之间的函数图象如图所示:
(1)月通话为100分钟时,应交话费 元;
(2)当x>100时,求y与x之间的函数关系式;
(3)月通话为280分钟时,应交话费多少元?
解:(1)观察图象可知月通话为100分钟时,应交话费40元;
(2) 设x>100时, y与x之间的函数关系式为y=kx+b
由图可知:x=100时,y=40;x=200时y=60
则有 , 解之得:
所求函数关系式为:
(3)把x=280代入关系式 得:y=76 即
月通话为280分钟时,应交话费76元.
例题讲解
4.为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过时,超过部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(1)求出y关于x的函数解析式;
解:y关于x的函数解析式为:
(1+0.3)x =1.3x, (0≤x≤8)
(1.5+1.2)(x-8)+1.3×8=2.7x-11.2. (x>8)
y=
例题讲解
(2)当x=10时,y=2.7×10-11.2=15.8.
(3)∵1.3×8=10.4<26.6,∴该用户用水量超过8立方米.
∴2.7x-11.2=26.6,解得x=14.
答:应缴水费为15.8元.
答:该户这月用水量为14立方米.
(2)该市一户某月若用水x=10立方米时,求应缴水费;
(3)该市一户某月缴水费26.6元,求该户这月用水量.
例题讲解
1.画分段函数图象的步骤:
①明确函数解析式分几段,以及对应的自变量取值范围是什么,解析式分别是什么;
②选取每一段自变量取值范围端点数值(或特殊值),分别代入对应的解析式计算对应的函数值,得到点的坐标;
③描点;④连线。
2.分段函数中函数自变量的取值范围不同,所对应的函数关系(图象)也不相同。
实际问题
数学问题
数学问题的解
建立函数模型
解函数问题
课堂小结
布置作业
教科书99页,习 题19.2 9, 11题
教科书第60页第3、6题
布置作业
再见
