5.7确定二次函数的解析式课件
图片预览



文档简介
(共12张PPT)
用待定系数法求二次函数的解析式
y
x
o
课 前 复 习
例 题 选 讲
课 堂 小 结
课 堂 练 习
温故知新
二次函数解析式有哪几种表达式?
一般式:y=ax2+bx+c
顶点式:y=a(x-h)2+k
两根式:y=a(x-x1)(x-x2)
例题
封面
例 题 选 讲
一般式: y=ax2+bx+c
两根式:
y=a(x-x1)(x-x2)
顶点式:
y=a(x-h)2+k
解:
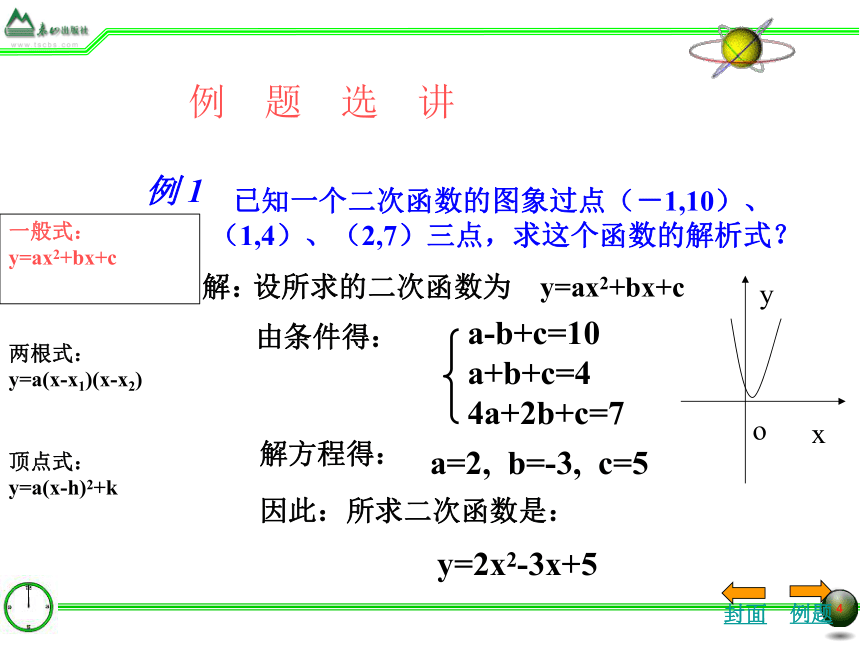
设所求的二次函数为 y=ax2+bx+c
由条件得:
a-b+c=10
a+b+c=4
4a+2b+c=7
解方程得:
因此:所求二次函数是:
a=2, b=-3, c=5
y=2x2-3x+5
已知一个二次函数的图象过点(-1,10)、
(1,4)、(2,7)三点,求这个函数的解析式?
o
x
y
例 1
例题
封面
例 题 选 讲
解:
设所求的二次函数为 y=a(x+1)2-3
由条件得:
已知抛物线的顶点为(-1,-3),与轴交点为
(0,-5)求抛物线的解析式?
y
o
x
点( 0,-5 )在抛物线上
a-3=-5, 得a=-2
故所求的抛物线解析式为 y=-2(x+1)2-3
即:y=-2x2-4x-5
一般式: y=ax2+bx+c
两根式:
y=a(x-x1)(x-x2)
顶点式:
y=a(x-h)2+k
例 2
例题
封面
例 题 选 讲
解:
设所求的二次函数为 y=a(x+1)(x-1)
由条件得:
已知抛物线与X轴交于A(-1,0),B(1,0)
并经过点M(0,1),求抛物线的解析式?
y
o
x
点M( 0,1 )在抛物线上
所以:a(0+1)(0-1)=1
得: a=-1
故所求的抛物线解析式为 y=- (x+1)(x-1)
即:y=-x2+1
一般式: y=ax2+bx+c
两根式:
y=a(x-x1)(x-x2)
顶点式:
y=a(x-h)2+k
例题
例 3
封面
例 题 选 讲
有一个抛物线形的立交桥拱(如图所示),这个桥拱的最大高度
为16m,跨度为40m.现把它的图形放在坐标系里
求抛物线的解析式.
例 4
设抛物线的解析式为y=ax2+bx+c,
解:
根据题意可知
抛物线经过(0,0),(20,16)和(40,0)三点
可得方程组
通过利用给定的条件
列出a、b、c的三元
一次方程组,求出a、
b、c的值,从而确定
函数的解析式.
过程较繁杂,
评价
封面
练习
例 题 选 讲
有一个抛物线形的立交桥拱,这个桥拱的最大高度
为16m,跨度为40m.现把它的图形放在坐标系里
(如图所示),求抛物线的解析式.
例 4
设抛物线为y=a(x-20)2+16
解:
根据题意可知
∵ 点(0,0)在抛物线上,
通过利用条件中的顶点和过原点选用顶点式求解,方法比较灵活
评价
∴ 所求抛物线解析式为
封面
练习
例 题 选 讲
有一个抛物线形的立交桥拱,这个桥拱的最大高度
为16m,跨度为40m.现把它的图形放在坐标系里
(如图所示),求抛物线的解析式.
例4
设抛物线为y=ax(x-40 )
解:
根据题意可知
∵ 点(20,16)在抛物线上,
选用两根式求解,方法灵活巧妙,过程也较简捷
评价
封面
练习
课 堂 练 习
一个二次函数,当自变量x= -3时,函数值y=2
当自变量x= -1时,函数值y= -1,当自变量x=1时
,函数值y= 3,求这个二次函数的解析式?
已知抛物线与X轴的两个交点的横坐标是 、 ,
与Y轴交点的纵坐标是,求这个抛物线的解析式?
3
2
1
2
1、
2、
封面
小结
归 纳 小 结
求二次函数解析式的一般方法:
已知图象上三点或三对的对应值,
通常选择一般式
已知图象的顶点坐标、对称轴或和最值)
通常选择顶点式
已知图象与x轴的两个交点的横x1、x2,
通常选择两根式
y
x
o
封面
确定二次函数的解析式时,应该根据条件的特点,
恰当地选用一种函数表达式,
用待定系数法求二次函数的解析式
y
x
o
课 前 复 习
例 题 选 讲
课 堂 小 结
课 堂 练 习
温故知新
二次函数解析式有哪几种表达式?
一般式:y=ax2+bx+c
顶点式:y=a(x-h)2+k
两根式:y=a(x-x1)(x-x2)
例题
封面
例 题 选 讲
一般式: y=ax2+bx+c
两根式:
y=a(x-x1)(x-x2)
顶点式:
y=a(x-h)2+k
解:
设所求的二次函数为 y=ax2+bx+c
由条件得:
a-b+c=10
a+b+c=4
4a+2b+c=7
解方程得:
因此:所求二次函数是:
a=2, b=-3, c=5
y=2x2-3x+5
已知一个二次函数的图象过点(-1,10)、
(1,4)、(2,7)三点,求这个函数的解析式?
o
x
y
例 1
例题
封面
例 题 选 讲
解:
设所求的二次函数为 y=a(x+1)2-3
由条件得:
已知抛物线的顶点为(-1,-3),与轴交点为
(0,-5)求抛物线的解析式?
y
o
x
点( 0,-5 )在抛物线上
a-3=-5, 得a=-2
故所求的抛物线解析式为 y=-2(x+1)2-3
即:y=-2x2-4x-5
一般式: y=ax2+bx+c
两根式:
y=a(x-x1)(x-x2)
顶点式:
y=a(x-h)2+k
例 2
例题
封面
例 题 选 讲
解:
设所求的二次函数为 y=a(x+1)(x-1)
由条件得:
已知抛物线与X轴交于A(-1,0),B(1,0)
并经过点M(0,1),求抛物线的解析式?
y
o
x
点M( 0,1 )在抛物线上
所以:a(0+1)(0-1)=1
得: a=-1
故所求的抛物线解析式为 y=- (x+1)(x-1)
即:y=-x2+1
一般式: y=ax2+bx+c
两根式:
y=a(x-x1)(x-x2)
顶点式:
y=a(x-h)2+k
例题
例 3
封面
例 题 选 讲
有一个抛物线形的立交桥拱(如图所示),这个桥拱的最大高度
为16m,跨度为40m.现把它的图形放在坐标系里
求抛物线的解析式.
例 4
设抛物线的解析式为y=ax2+bx+c,
解:
根据题意可知
抛物线经过(0,0),(20,16)和(40,0)三点
可得方程组
通过利用给定的条件
列出a、b、c的三元
一次方程组,求出a、
b、c的值,从而确定
函数的解析式.
过程较繁杂,
评价
封面
练习
例 题 选 讲
有一个抛物线形的立交桥拱,这个桥拱的最大高度
为16m,跨度为40m.现把它的图形放在坐标系里
(如图所示),求抛物线的解析式.
例 4
设抛物线为y=a(x-20)2+16
解:
根据题意可知
∵ 点(0,0)在抛物线上,
通过利用条件中的顶点和过原点选用顶点式求解,方法比较灵活
评价
∴ 所求抛物线解析式为
封面
练习
例 题 选 讲
有一个抛物线形的立交桥拱,这个桥拱的最大高度
为16m,跨度为40m.现把它的图形放在坐标系里
(如图所示),求抛物线的解析式.
例4
设抛物线为y=ax(x-40 )
解:
根据题意可知
∵ 点(20,16)在抛物线上,
选用两根式求解,方法灵活巧妙,过程也较简捷
评价
封面
练习
课 堂 练 习
一个二次函数,当自变量x= -3时,函数值y=2
当自变量x= -1时,函数值y= -1,当自变量x=1时
,函数值y= 3,求这个二次函数的解析式?
已知抛物线与X轴的两个交点的横坐标是 、 ,
与Y轴交点的纵坐标是,求这个抛物线的解析式?
3
2
1
2
1、
2、
封面
小结
归 纳 小 结
求二次函数解析式的一般方法:
已知图象上三点或三对的对应值,
通常选择一般式
已知图象的顶点坐标、对称轴或和最值)
通常选择顶点式
已知图象与x轴的两个交点的横x1、x2,
通常选择两根式
y
x
o
封面
确定二次函数的解析式时,应该根据条件的特点,
恰当地选用一种函数表达式,
