北师大版七下 1.4 整式的乘法 知识点强化课件(32张)
文档属性
| 名称 | 北师大版七下 1.4 整式的乘法 知识点强化课件(32张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-08 00:00:00 | ||
图片预览











文档简介
1.4 整式的乘法(1)
北师大版 七年级数学下册
教学目录
1.课堂基础训练
2.培优提高训练
·
◆ 课堂基础训练 ◆
一、选择题。
1.计算a·3a的结果是 ( )
A.a2 B.3a2 C.3a D.4a
2.计算2a2b3·(-3a)的结果是 ( )
A.-6a3b3 B.6a2b3
C.6a3b3 D.-6a2b3
B
A
3.若 ·3xy=27x3y4,则 内应填的单项式是 ( )
A.3x3y4 B.9x2y2 C.3x2y3 D.9x2y3
4.下列运算正确的是 ( )
A.x2·x3=x6 B.(2x3)2=2x6
C.x4+x2=x6 D.2x·5x4=10x5
D
D
二、填空题。
1.(2a2)·(3a)= .?
2.(-2x2y3)·3xy2= .?
3.-3a2b3·(-2a2b)= .?
4.(-2a)2·3a4= .?
5.(6×105)×(7×103)= .?
6.?12????????32·4x2y= .?
7.(-ab5)2·(-2a2b)3= .?
?
6a3
-6x3y5
6a4b4
12a6
4.2×109
x4y7
-8a8b13
三、解答题。
1.计算下列各题.
(1) 4x2·(-2xy);
解:原式=-8x3y.
?
(2) -2x3y2·(x2y3)2;
解:原式=-2x3y2·x4y6=-2x7y8.
(3) (-ab3)2·(-a2b);
解:原式=a2b6·(-a2b)=-a4b7.
?
(4) (-x2y)3·?23????????·34x.
解:原式=(-x6y3)·?23????????·34x=12x8y4.
?
2.先化简,再求值.
(-3ab)·(-a2c)·6ab2,其中a=-3,b=13,c=1.
解:原式=18a4b3c=18×(-3)4×133×1=54.
?
◆ 培优提高训练 ◆
1.(1)先化简,再求值:
2x2y(-2xy2)3+(2xy)3(-xy2)2,其中x=4,y=14;
解:原式=2x2y·(-8x3y6)+8x3y3·x2y4
=-16x5y7+8x5y7=-8x5y7,当x=4,
y=14时,原式=-12.
?
(2)已知(-2axby2c)(3xb-1y)=12x11y7,求a+b+c的值.
解:∵(-2axby2c)(3xb-1y)=12x11y7,
∴-6ax2b-1y2c+1=12x11y7,
∴a=-2,b=6,c=3,
∴a+b+c=-2+6+3=7.
?
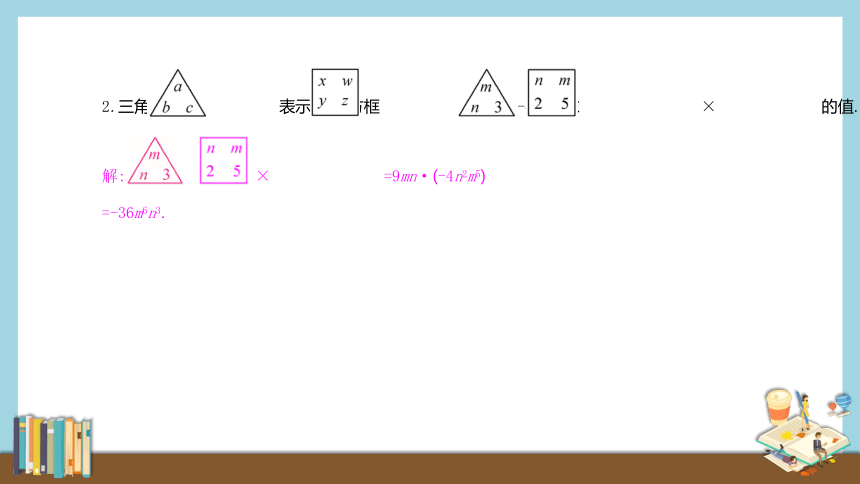
2.三角 表示3abc,方框 表示-4xywz,求 × 的值.
解: × =9mn·(-4n2m5)
=-36m6n3.
1.4 整式的乘法(2)
北师大版 七年级数学下册
教学目录
1.课堂基础训练
2.培优提高训练
·
◆ 课堂基础训练 ◆
一、选择题。
1.计算x(x+y)的结果是 ( )
A.x+xy B.x2+y
C.x2+xy D.2x+xy
2.计算?12????????·(a2-2ab-1)的结果是 ( )
A.-12a3b+a2b2
B.12a3b-a2b2-12ab
C.-12a3b+a2b2+12ab
D.-12a3b-a2b2-12ab
?
C
C
3.下列运算中,正确的是 ( )
A.-2x(3x2y-2xy)=-6x3y-4x2y
B.2xy2(-x2+2y2+1)=-4x3y4
C.(3ab2-2ab)·abc=3a2b3-2a2b2
D.(ab)2(2ab2-c)=2a3b4-a2b2c
4.当a-2b=2时,则代数式4a-8b-6的值为 ( )
A.14 B.-2 C.-4 D.2
D
D
二、填空题。
1.计算:2a32?????1= .?
2.计算:(2a2+a-1)12????= .?
3.计算:(2x3-3x2+4x-1)·(-2x)2= .?
?
3a2-2a
a3+12a2-12a
?
8x5-12x4+16x3-4x2
三、解答题。
1.计算下列各题.
(1) 3????2?43????+12·6xy;
解:原式=(3x2)·6xy+?43????·6xy+12·6xy=18x3y-8xy2+3xy.
?
(2) (-3a4)2-2a3a5;
解:原式=9a8-2a8=7a8.
?
(3) 2x(-x2+3x-4)-3x212????+1;
解:原式=-2x3+6x2-8x-32x3-3x2
=-72x3+3x2-8x.
?
(4) -3x2·13?????????????2-10x·(x2y-xy2).
解:原式=-x3y+3x2y2-10x3y+10x2y2
=13x2y2-11x3y.
?
2.计算下图中阴影部分的面积.
解:b(2b+a)-12πb2=2b2+ab-12πb2.
?
◆ 培优提高训练 ◆
1.先化简,再求值.
(1) 2x2(x2-x+1)-x(2x3-10x2+2x),其中x=-12;
解:原式=2x4-2x3+2x2-2x4+10x3-2x2
=8x3,当x=-12时,原式=8×?123
=-1.
?
(2) x(x2+3)+x2(x-3)-3x(x2-x-1),其中x=12.
解:原式=x3+3x+x3-3x2-3x3+3x2+3x=-x3+6x,当x=12时,原式=-123+6×12=3-18=278.
?
2.某同学在计算一个多项式乘以-3x2时,算成了加上-3x2,得到的答案是x2-12x+1,那么正确的计算结果是多少?
解:设这个多项式为A,则A+(-3x2)=x2-12x+1,∴A=4x2-12x+1,∴A·(-3x2)
=(4x2-12x+1)·(-3x2)
=-12x4+32x3-3x2.
?
3.当m,n为何值时,12x[x(x+m)+nx(x+1)+m=的展开式中不含x2项和x3项?
解:12x[x(x+m)+nx(x+1)+m
=12x(x2+mx+nx2+nx+m)
=12(1+n)x3+12(m+n)x2+12mx,
因为它不含x2项和x3项,
所以1+n=0,m+n=0.解得n=-1,m=1.
?
4.已知x2+x+1=2.求x4+2x3+x2+2的值.
解:∵x2+x+1=2,∴x2+x=1.
∵原式=x4+x3+x3+x2+2
=x2(x2+x)+x(x2+x)+2
=(x2+x)(x2+x)+2=1×1+2=3.
1.4 整式的乘法(3)
北师大版 七年级数学下册
教学目录
1.课堂基础训练
2.培优提高训练
·
◆ 课堂基础训练 ◆
一、选择题。
1.下列计算正确的是 ( )
A.(x+1)(x+2)=x2+2
B.(x+y)(x2+y2)=x3+y3
C.(x-2)(x+1)=x2-x-2
D.(x-2)(x-1)=x2-2x+2
2.计算(x-2)(x-3)的结果是 ( )
A.x2-5x+6 B.x2-5x-6
C.x2+5x-6 D.x2+5x+6
C
A
3.计算(2m+3)(m-1)的结果是 ( )
A.2m2-m-3 B.2m2+m-3
C.2m2-m+3 D.m2-m-3
4.已知x2-4x-1=0,则代数式x(x-4)+1的值为 ( )
A.2 B.1 C.0 D.-1
5.若(x+1)(x-3)=x2+mx+n,则m+n的值是 ( )
A.-5 B.-2 C.-1 D.1
B
A
A
二、填空题。
1.(x+3)(x-7)= .?
2.(2x+5)(3x-2)= .?
3.(2x-1)(3x2+2x+1)= .?
4.若(x-m)(x+n)=x2-5x-6,则m+n的值为 .?
5.(2x3-3x2+4x-1)·(-2x)2= .?
x2-4x-21
6x2+11x-10
6x3+x2-1
7
8x5-12x4+16x3-4x2
三、解答题。
计算下列各题.
(1) (2x-3y)(4x+5y);
解:原式=8x2+10xy-12xy-15y2
=8x2-2xy-15y2.
?
(2) 4m(m-n)+(5m-n)(m+n);
解:原式=4m2-4mn+5m2+5mn-mn-n2
=9m2-n2.
(3) (m+2n)(m-2n);
解:原式=m2-2mn+2mn-4n2=m2-4n2.
?
(4) (3a-2b)(2a+b-4).
解:原式=6a2+3ab-4ab-12a-2b2+8b=
6a2-ab-2b2-12a+8b.
◆ 培优提高训练 ◆
1.解方程:(2x+3)(5x+7)=2(5x+6)(x+1).
解:10x2+14x+15x+21=10x2+22x+12,
10x2-10x2+29x-22x=12-21,7x=-9,x=-97.
2.请说明对任意正整数n,式子n(n+5)-(n+2)(n-3)的值必定能被6整除.
解:原式=n2+5n-n2+n+6=6n+6=6(n+1),
∵n是整数,∴式子n(n+5)-(n+2)(n-3)的值必定能被6整除.
?
3.小思同学用若干张如图所示的A,B,C三类卡片,拼出了一个长为2a+b、宽为a+b的长方形图形.请你通过计算求出小思同学拼这个长方形所用A,B,C三类卡片各几张(要求:所拼图形中,卡片之间不能重叠,不能有空隙).
解:因为(2a+b)(a+b)=2a2+3ab+b2,所以所用A,B,C三类卡片分别为3张,1张,2张.
感谢观看^_^
北师大版 七年级数学下册
北师大版 七年级数学下册
教学目录
1.课堂基础训练
2.培优提高训练
·
◆ 课堂基础训练 ◆
一、选择题。
1.计算a·3a的结果是 ( )
A.a2 B.3a2 C.3a D.4a
2.计算2a2b3·(-3a)的结果是 ( )
A.-6a3b3 B.6a2b3
C.6a3b3 D.-6a2b3
B
A
3.若 ·3xy=27x3y4,则 内应填的单项式是 ( )
A.3x3y4 B.9x2y2 C.3x2y3 D.9x2y3
4.下列运算正确的是 ( )
A.x2·x3=x6 B.(2x3)2=2x6
C.x4+x2=x6 D.2x·5x4=10x5
D
D
二、填空题。
1.(2a2)·(3a)= .?
2.(-2x2y3)·3xy2= .?
3.-3a2b3·(-2a2b)= .?
4.(-2a)2·3a4= .?
5.(6×105)×(7×103)= .?
6.?12????????32·4x2y= .?
7.(-ab5)2·(-2a2b)3= .?
?
6a3
-6x3y5
6a4b4
12a6
4.2×109
x4y7
-8a8b13
三、解答题。
1.计算下列各题.
(1) 4x2·(-2xy);
解:原式=-8x3y.
?
(2) -2x3y2·(x2y3)2;
解:原式=-2x3y2·x4y6=-2x7y8.
(3) (-ab3)2·(-a2b);
解:原式=a2b6·(-a2b)=-a4b7.
?
(4) (-x2y)3·?23????????·34x.
解:原式=(-x6y3)·?23????????·34x=12x8y4.
?
2.先化简,再求值.
(-3ab)·(-a2c)·6ab2,其中a=-3,b=13,c=1.
解:原式=18a4b3c=18×(-3)4×133×1=54.
?
◆ 培优提高训练 ◆
1.(1)先化简,再求值:
2x2y(-2xy2)3+(2xy)3(-xy2)2,其中x=4,y=14;
解:原式=2x2y·(-8x3y6)+8x3y3·x2y4
=-16x5y7+8x5y7=-8x5y7,当x=4,
y=14时,原式=-12.
?
(2)已知(-2axby2c)(3xb-1y)=12x11y7,求a+b+c的值.
解:∵(-2axby2c)(3xb-1y)=12x11y7,
∴-6ax2b-1y2c+1=12x11y7,
∴a=-2,b=6,c=3,
∴a+b+c=-2+6+3=7.
?
2.三角 表示3abc,方框 表示-4xywz,求 × 的值.
解: × =9mn·(-4n2m5)
=-36m6n3.
1.4 整式的乘法(2)
北师大版 七年级数学下册
教学目录
1.课堂基础训练
2.培优提高训练
·
◆ 课堂基础训练 ◆
一、选择题。
1.计算x(x+y)的结果是 ( )
A.x+xy B.x2+y
C.x2+xy D.2x+xy
2.计算?12????????·(a2-2ab-1)的结果是 ( )
A.-12a3b+a2b2
B.12a3b-a2b2-12ab
C.-12a3b+a2b2+12ab
D.-12a3b-a2b2-12ab
?
C
C
3.下列运算中,正确的是 ( )
A.-2x(3x2y-2xy)=-6x3y-4x2y
B.2xy2(-x2+2y2+1)=-4x3y4
C.(3ab2-2ab)·abc=3a2b3-2a2b2
D.(ab)2(2ab2-c)=2a3b4-a2b2c
4.当a-2b=2时,则代数式4a-8b-6的值为 ( )
A.14 B.-2 C.-4 D.2
D
D
二、填空题。
1.计算:2a32?????1= .?
2.计算:(2a2+a-1)12????= .?
3.计算:(2x3-3x2+4x-1)·(-2x)2= .?
?
3a2-2a
a3+12a2-12a
?
8x5-12x4+16x3-4x2
三、解答题。
1.计算下列各题.
(1) 3????2?43????+12·6xy;
解:原式=(3x2)·6xy+?43????·6xy+12·6xy=18x3y-8xy2+3xy.
?
(2) (-3a4)2-2a3a5;
解:原式=9a8-2a8=7a8.
?
(3) 2x(-x2+3x-4)-3x212????+1;
解:原式=-2x3+6x2-8x-32x3-3x2
=-72x3+3x2-8x.
?
(4) -3x2·13?????????????2-10x·(x2y-xy2).
解:原式=-x3y+3x2y2-10x3y+10x2y2
=13x2y2-11x3y.
?
2.计算下图中阴影部分的面积.
解:b(2b+a)-12πb2=2b2+ab-12πb2.
?
◆ 培优提高训练 ◆
1.先化简,再求值.
(1) 2x2(x2-x+1)-x(2x3-10x2+2x),其中x=-12;
解:原式=2x4-2x3+2x2-2x4+10x3-2x2
=8x3,当x=-12时,原式=8×?123
=-1.
?
(2) x(x2+3)+x2(x-3)-3x(x2-x-1),其中x=12.
解:原式=x3+3x+x3-3x2-3x3+3x2+3x=-x3+6x,当x=12时,原式=-123+6×12=3-18=278.
?
2.某同学在计算一个多项式乘以-3x2时,算成了加上-3x2,得到的答案是x2-12x+1,那么正确的计算结果是多少?
解:设这个多项式为A,则A+(-3x2)=x2-12x+1,∴A=4x2-12x+1,∴A·(-3x2)
=(4x2-12x+1)·(-3x2)
=-12x4+32x3-3x2.
?
3.当m,n为何值时,12x[x(x+m)+nx(x+1)+m=的展开式中不含x2项和x3项?
解:12x[x(x+m)+nx(x+1)+m
=12x(x2+mx+nx2+nx+m)
=12(1+n)x3+12(m+n)x2+12mx,
因为它不含x2项和x3项,
所以1+n=0,m+n=0.解得n=-1,m=1.
?
4.已知x2+x+1=2.求x4+2x3+x2+2的值.
解:∵x2+x+1=2,∴x2+x=1.
∵原式=x4+x3+x3+x2+2
=x2(x2+x)+x(x2+x)+2
=(x2+x)(x2+x)+2=1×1+2=3.
1.4 整式的乘法(3)
北师大版 七年级数学下册
教学目录
1.课堂基础训练
2.培优提高训练
·
◆ 课堂基础训练 ◆
一、选择题。
1.下列计算正确的是 ( )
A.(x+1)(x+2)=x2+2
B.(x+y)(x2+y2)=x3+y3
C.(x-2)(x+1)=x2-x-2
D.(x-2)(x-1)=x2-2x+2
2.计算(x-2)(x-3)的结果是 ( )
A.x2-5x+6 B.x2-5x-6
C.x2+5x-6 D.x2+5x+6
C
A
3.计算(2m+3)(m-1)的结果是 ( )
A.2m2-m-3 B.2m2+m-3
C.2m2-m+3 D.m2-m-3
4.已知x2-4x-1=0,则代数式x(x-4)+1的值为 ( )
A.2 B.1 C.0 D.-1
5.若(x+1)(x-3)=x2+mx+n,则m+n的值是 ( )
A.-5 B.-2 C.-1 D.1
B
A
A
二、填空题。
1.(x+3)(x-7)= .?
2.(2x+5)(3x-2)= .?
3.(2x-1)(3x2+2x+1)= .?
4.若(x-m)(x+n)=x2-5x-6,则m+n的值为 .?
5.(2x3-3x2+4x-1)·(-2x)2= .?
x2-4x-21
6x2+11x-10
6x3+x2-1
7
8x5-12x4+16x3-4x2
三、解答题。
计算下列各题.
(1) (2x-3y)(4x+5y);
解:原式=8x2+10xy-12xy-15y2
=8x2-2xy-15y2.
?
(2) 4m(m-n)+(5m-n)(m+n);
解:原式=4m2-4mn+5m2+5mn-mn-n2
=9m2-n2.
(3) (m+2n)(m-2n);
解:原式=m2-2mn+2mn-4n2=m2-4n2.
?
(4) (3a-2b)(2a+b-4).
解:原式=6a2+3ab-4ab-12a-2b2+8b=
6a2-ab-2b2-12a+8b.
◆ 培优提高训练 ◆
1.解方程:(2x+3)(5x+7)=2(5x+6)(x+1).
解:10x2+14x+15x+21=10x2+22x+12,
10x2-10x2+29x-22x=12-21,7x=-9,x=-97.
2.请说明对任意正整数n,式子n(n+5)-(n+2)(n-3)的值必定能被6整除.
解:原式=n2+5n-n2+n+6=6n+6=6(n+1),
∵n是整数,∴式子n(n+5)-(n+2)(n-3)的值必定能被6整除.
?
3.小思同学用若干张如图所示的A,B,C三类卡片,拼出了一个长为2a+b、宽为a+b的长方形图形.请你通过计算求出小思同学拼这个长方形所用A,B,C三类卡片各几张(要求:所拼图形中,卡片之间不能重叠,不能有空隙).
解:因为(2a+b)(a+b)=2a2+3ab+b2,所以所用A,B,C三类卡片分别为3张,1张,2张.
感谢观看^_^
北师大版 七年级数学下册
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
