8.5怎样判定三角形相似(一)

(共23张PPT)
（青岛版）八年级 数学下册 8.5 怎样判定相似三角形
*
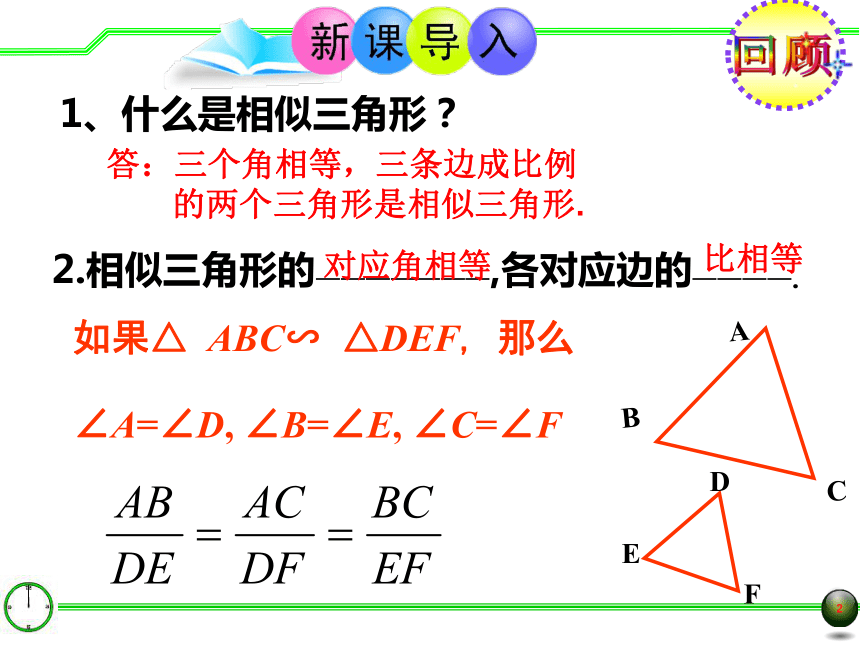
1、什么是相似三角形？
答：三个角相等，三条边成比例
的两个三角形是相似三角形.
A
B
C
D
E
F
2.相似三角形的———————,各对应边的————.
对应角相等
比相等
如果△ ABC∽ △DEF, 那么
∠A=∠D, ∠B=∠E, ∠C=∠F
3、三角形全等的判定方法有哪些？
答：1.利用全等三角形的定义，
即三对角和三对边分别对应相等.
2.利用全等三角形的四个判定定理:
(ASA，AAS，SAS，SSS）．
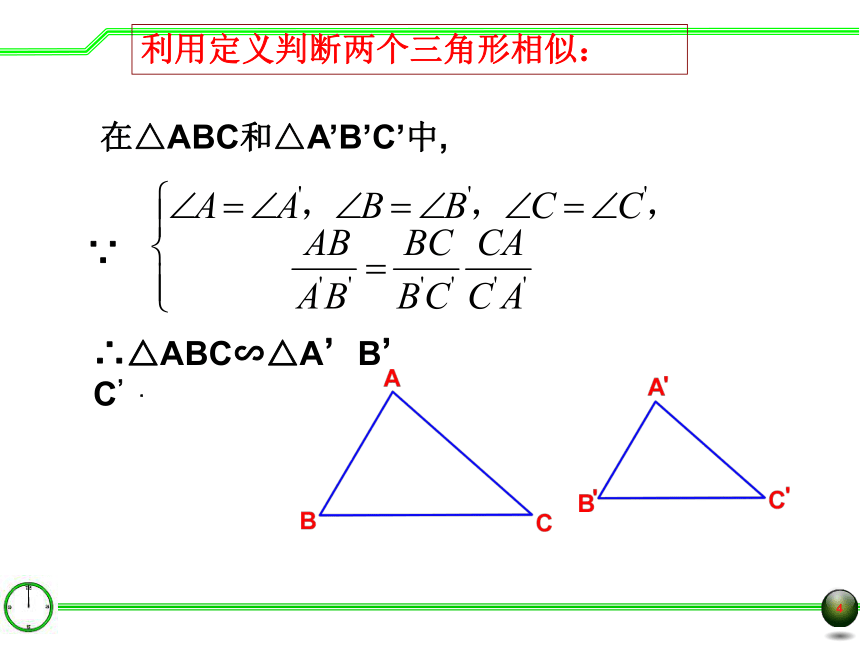
在△ABC和△A’B’C’中,
∴△ABC∽△A’B’C’.
∵
利用定义判断两个三角形相似：
学习三角形全等时，我们知道，除了可以利用定义法证明对应角相等，对应边相等来判定两个三角形全等外，还有判定的简便方法（SSS，SAS，ASA，AAS）．类似地，判定两个三角形相似时，是不是除了定义法，对所有的对应角和对应边都要一一验证呢？
1.经历判定两个三角形相似条件的探索过程；积累数学活动的经验；
2.掌握三角形相似的判定方法1，会利用三角形相似解决一些简单的实际问题；
3. 在探索及解决问题的过程中，丰富学生数学活动的经验，发展合情推理能力，能有条理地、清晰地进行推理。
重点：理解并熟练掌握判定方法1成立的条件和推导过程，且 能熟练地推导证明.
难点：探索及证明相似三角形的判定方法.
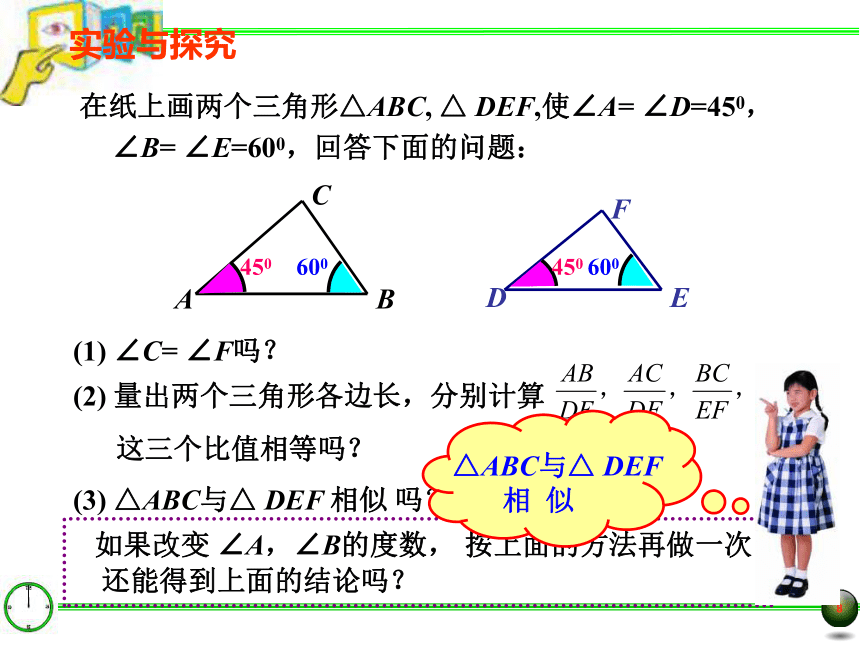
实验与探究
在纸上画两个三角形△ABC, △ DEF,使∠A= ∠D=450， ∠B= ∠E=600，回答下面的问题：
A
B
C
450
600
D
E
F
450
600
(1) ∠C= ∠F吗？
(2) 量出两个三角形各边长，分别计算
这三个比值相等吗？
(3) △ABC与△ DEF 相似 吗？
如果改变 ∠A，∠B的度数， 按上面的方法再做一次，还能得到上面的结论吗？
△ABC与△ DEF
相 似
判定方法1 如果一个三角形的两个角与另一个三角形的两个角分别相等，那么这两个三角形相似.
符号语言：在△ABC与△ DEF 中 ，
∵ ∠A= ∠D， ∠B= ∠E，
∴ △ABC ∽△ DEF .
A
B
C
D
E
F
简记为：两对角分别相等的两个三角形相似.
１、两个全等三角形一定相似吗？为什么？
２、两个直角三角形一定相似吗？为什么？
两个等腰直角三角形呢？
３、两个等腰三角形一定相似吗？为什么？
两个等边三角形呢？
300
450
例1. 如图，在阳光下，为了测量学校水塔的高度，小亮走进水塔的影子里，使自己的影子刚好被水塔的影子遮住.已知小亮的身高BC=1.6米，此时，他的影子的长AC=1米，他距水塔的底部E处11.5米，水塔的顶部为点D.
（1）图中的△ABC与△ ADE相似吗？为什么？
（2）你能由此水塔的高度DE吗？
A
B
C
E
D
解：
（1） △ABC∽△ DEF .
理由：∵∠BAC =∠DAE, ∠BCA =∠DEA=900,
由判定方法1，∴△ABC∽△DEF .
（2） ∵△ABC∽△ DEF ，
∴
又∵AC=1米，CE=11.5米，BC=1.6米，AE=AC+CE=1+11.5=12.5（米）
∴ 于是 DE=20（米）.
因此水塔的高度为20米.
A
B
C
E
D
如图,身高为1.60m的某学生想测量一棵大树的高度,他沿着树影BA由B向A走去,当走到C点时,他的影子顶端正好与树的影子顶端重合,测得BC＝3.2m,CA=0.8m,则树的高度为（　 ）
A
B
C
A.4.8m B.6.4m
C.8m D.10m
3.2m
0.8m
1.6m
例1 还有别的测量方法吗？
仿照例1，你会测量操场上旗杆的高度吗？
测量报告
小组成员：
你们选用的测量工具是：
测量方案示意图：
过程感想：
简要说明：
问题：用你想到的可行方案，和小组成员合作，测量学校中旗杆的高度。
相似三角形的识别方法有那些？
方法1：通过定义
方法2：判定定理1.两角对应相等。
在ΔABC 和 ΔA'B'C'中，
∵ ∠A=∠A'， ∠B=∠B'
∴ ΔABC ∽ ΔA'B'C'
用数学符号表示：
C
A
A'
B
B'
C'
1、判断题：
⑴ 所有的直角三角形都相似 . （ ）
⑵ 所有的等边三角形都相似. （ ）
⑶ 所有的等腰直角三角形都相似. （ ）
⑷ 有一个角相等的两等腰三角形相似 . （ ）
（5）有一个锐角相等的两个直角三角形相似. （ ）
（6）平行于三角形一边的直线截三角形的两边，截得的三角形和原三角形相似. （ ）
×
√
√
×
√
√
C
B
A
E
D
E
D
A
C
B
C
B
A
E
D
A
B
C
A’
B’
C’
2、下列图形中两个三角形是否相似？
A
B
C
D
E
A
B
C
A’
C’
B’
A
B
C
D
E
(1)
(2)
(3)
(4)
3.　如图，为了估算河的宽度，我们可以在河对岸选定一个目标作为点A，再在河的这一边选点B和C，使AB⊥BC，然后，再选点E，使EC⊥BC，用视线确定BC和AE的交点D．此时如果测得BD＝120米，DC＝60米，EC＝50米，求两岸间的大致距离AB．
A
E
D
C
B
50m
120m
60m

1.已知等腰三角形ABC和等腰三角形DEF,
∠A= ∠D=500，这两个三角形一定相似吗？
E
A
B
C
F
D
2.已知：CD是Rt△ABC的斜边AB上的高.
（1） △ABC 与△ACD 相似吗？;
（2） △ACD 与△CBD相似吗？如果相似，
请说明理由.
A
D
B
C
课本P48 A组 1、2、3
导学达标案
*