高中数学新课标A版必修1第三章 函数的应用单元测试
文档属性
| 名称 | 高中数学新课标A版必修1第三章 函数的应用单元测试 | 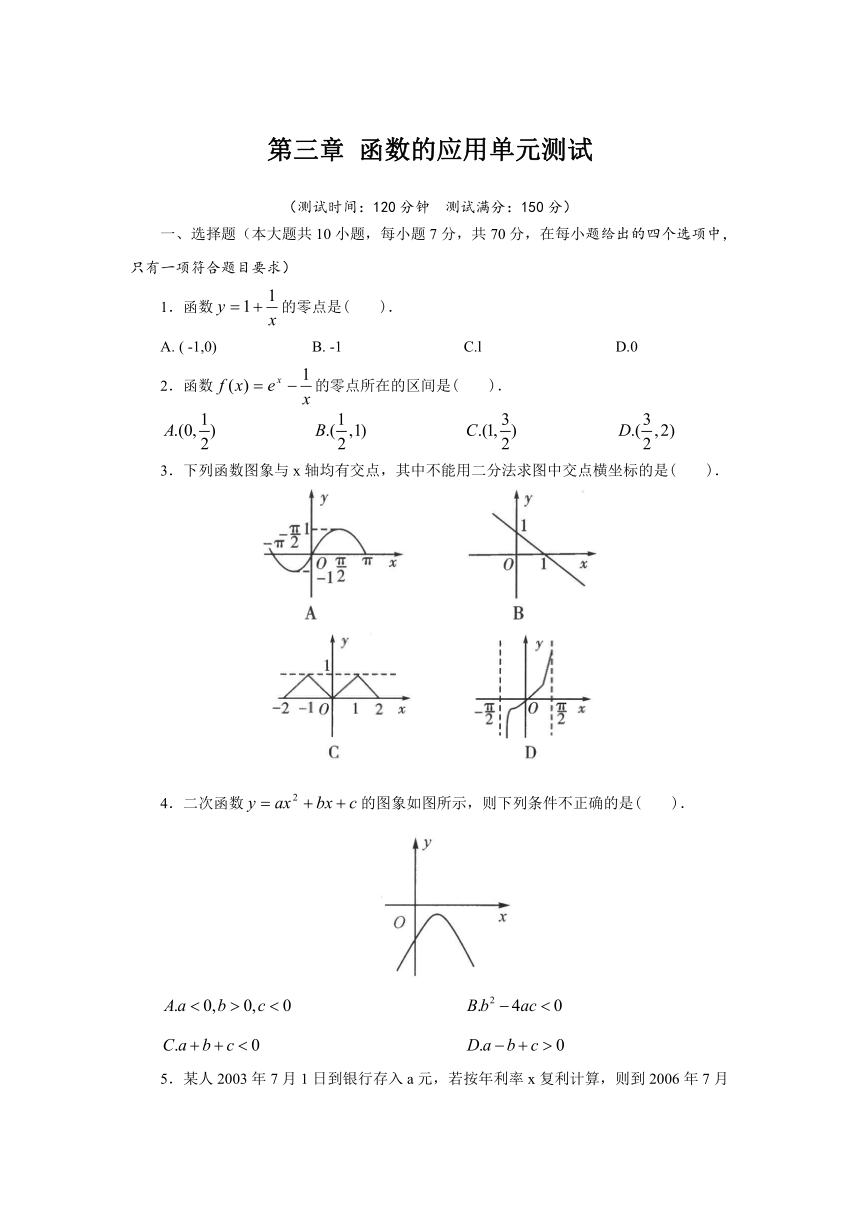 | |
| 格式 | zip | ||
| 文件大小 | 167.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-14 20:15:42 | ||
图片预览




文档简介
第三章 函数的应用单元测试
(测试时间:120分钟 测试满分:150分)
一、选择题(本大题共10小题,每小题7分,共70分,在每小题给出的四个选项中,只有一项符合题目要求)
1.函数的零点是( ).
A. ( -1,0) B. -1 C.l D.0
2.函数的零点所在的区间是( ).
3.下列函数图象与x轴均有交点,其中不能用二分法求图中交点横坐标的是( ).
4.二次函数的图象如图所示,则下列条件不正确的是( ).
5.某人2003年7月1日到银行存入a元,若按年利率x复利计算,则到2006年7月1日可取款( )
元 元
元 元
6.某宾馆共有客床100张,各床每晚收费10元时可全部客满,若每晚收费每提高2元,便减少10张客床租出,为了获得最大利润,每床每晚收费提高( ).
A.2元 B.4元 C.6元 D.8元
7.函数有两个零点,则( ).
8.某企业生产总值的月平均增长率为P,则年平均增长率为( )
9.如图所示,阴影部分的面积S是h的函数(0≤h≤H),则该函数的图象是哪一个( ).
10.某商店计划投入资金20万元经销甲或乙两种商品,已知经销甲商品与乙商品所获得的利润分别为P(万元)和Q(万元),且它们与投入资金x(万元)的关系是;若不管资金如何投放,经销这两种商品或其中的一种商品所获得的纯利润总不少于5万元,则a的最小值应为( ).
二、填空题(本大题共5小题,每小题7分,共35分.把答案填在题中的横线上)
11.1992年底,世界人口已达到54.8亿,若世界人口的年平均增长率为x,2008年底人口数为y亿,那么y与x之间的关系式为 .
12.函数f(x)=x+b有一个零点2,那么函数的零点是 .
13.用二分法求方程在区间(2,4)上实数根时,取中点则下一个有根区间是 .
14.芒幕电子公司7年来,生产VCD总产量y(万台,即前t年年产量的和)与时间t(年)的函数关系式如图所示,下列4种说法:
①前3年中,产量增长的速度越来越快;
②前3年中,产量增长的速度越来越慢;
③第3年后,这种产品停止生产;
④第3年后,年产量保持为100万台.
其中正确的说法是 .(把正确说法的序号填上即可)
15.函数的零点均是正数,则实数m的取值范围是 .
三、解答题(本大题共4小题,共45分,解答时应写出文字说明、证明过程或演算步骤)
16.(10分)求方程的近似解(精确度为0.1).
17.(10分)将长度为1的铁丝分成两段,分别围成一个正方形和一个圆形,要使正方形与圆的面积之和最小,正方形的周长应为多少?
18.(12分)某影院共有1000个座位,票价不分等次.根据该影院的经营经验,当每张票价不超过10元时,票可全部售出,当每张票价高于10元时,每提高1元,将有30张票不能售出.为了获得更好的收益,需给影院定一个合适的票价,应符合的基本条件是:①为方便找零和算账,票价定为1元的整数倍;②影院放映一场电影的成本费用支出为5 750元,票房收入必须高于成本支出,用x(元)表示每张票价,用y(元)表示该影院放映一场的净收入(除去成本费用支出后的收入).
(1)用y表示为x的函数,并求其定义域;
(2)试问在符合基本条件的前提下,每张票价定为多少元时,放映一场的净收入最多?
19.(13分)以x为自变量的二次函数中,m是不小于零的整数,它的图象与x轴交于点A和点B,点A在原点左边,点B在原点右边.
(1)求这个二次函数的解析式;
(2)一次函数y=kx+b的图象经过点A,与这个二次函数的图象交于点C,且.求一次函数的解析式.
参考答案:
1.B
2.B【提示】计算得,则有
3.C
4.D【提示】抛物线开口向下,a<0,又对称轴在y轴右侧,
,b与a异号,b>0,抛物线与y轴交于负半轴,c<0,A正确.抛物线与x轴没有交点,B正确.抛物线全落在x轴下方,不论x取何值,y均小于O,故x=l时,y=a+b+c<0,C正确.x=-1时,y=a-b+c<0,D不正确.
5.D
6.C【提示】设每床每晚收费提高x元,则总收入y与x之间的关系为
所以当x=4,x=6时,y都取最大,结合实际,应选C.
7.B【提示】令由题意即要求两函数图象有两交点,利用数形结合思想,作出两函数图象,得k>0.
8.C【提示】可以由头年1月到第二年1月份来计算.
9.C【提示】当时,对应阴影部分的面积小于整个半圆面积的一半,且随着h的增大,S随之减小,故排除A、B、D,选择C.
10.A【提示】总利润y是一关于x的函数,利用函数值不小于5,可确定a的不等式,找出a的最小值,
设投放x万元经销甲商品,则经销乙商品投放(20 - x)万元,总利润
则即对恒成立,
而的最大值为,且x =20时,
也成立,故应选A.
11.【提示】1年后,世界人口数为54.8(1+x);
2年后,世界人口数为
3年后,世界人口数为
……
16年后即2008年底,世界人口数
12.【提示】由题意得2+b =0,即b= -2,则即函数的零点是
13.(2,3)【提示】设则有,则下一个有根区间是(2,3).
14.②③【提示】在区间[0,3]上,函数图象越来越远离y轴,则前3年中,产量增长的速度越来越慢,则①错,②正确;在区间(3,7]上,函数图象是平行于x轴的线段,说明没有变化,所以第3年后,这种产品停止生产,则③正确,④错误.
15.(0,1]【提示】设是函数f(x)的零点,
则有即’解得
16.解:令
函数f(x)的正零点在区间(1,2)内.
取(1,2)中点
取(1,1.5)中点
取(1. 25,1.5)中点
取(l. 375,1.5)中点
取(1.437 5,1.5).
方程的近似解为x=1.5.
【提示】转化为求函数的零点,确定函数零点所在的区间,用二分法求其近似解.
17.解:设正方形周长为x时,正方形与圆的面积之和为S.
则正方形边长为,圆周长为1 -x,圆半径为
则
当时,S有最小值,
此时正方形的周长为
【提示】建立函数模型,转化为求函数的最值.
18.解:(1)由题意知当x≤10时,y=1 000x -5 750.
当x>10时,
由解之得:
又所求函数表达式为
其定义域为.
(2)当时,x=10时,
当N)时
时,
每张票价为22元时净收入最多.
19.解:(1)抛物线与x轴有两个交点,关于x的方程有两个不相等的实数根,,解得m<2.
又m为不小于零的整数,m=0或1.
又抛物线与x轴的这两个交点,一个在原点的左边,另一个在原点的右边.
,即
当m=0时,,符合题意,当时,,不符合题意,应舍去.
只能取m=0.原二次函数的解析式为
即
(2)由(1)得A(1,0)、B(3,0),AB=4.
设点C的坐标为,则
又抛物线的开口向下,顶点坐标是(1,4).即抛物线上在x轴上方的任何一点的纵坐标都不能大于4.
点C在抛物线x轴下方的部分上,
,解得或
点C的坐标是(-2,-5)或(4,-5).
一次函数解析式为y= kx+b. ①
将A(1,0)、C(2,5)代入①,
得解得
将A(-1,0)、C(4,-5)代入①,得
解得
故所求一次函数解析式为
(测试时间:120分钟 测试满分:150分)
一、选择题(本大题共10小题,每小题7分,共70分,在每小题给出的四个选项中,只有一项符合题目要求)
1.函数的零点是( ).
A. ( -1,0) B. -1 C.l D.0
2.函数的零点所在的区间是( ).
3.下列函数图象与x轴均有交点,其中不能用二分法求图中交点横坐标的是( ).
4.二次函数的图象如图所示,则下列条件不正确的是( ).
5.某人2003年7月1日到银行存入a元,若按年利率x复利计算,则到2006年7月1日可取款( )
元 元
元 元
6.某宾馆共有客床100张,各床每晚收费10元时可全部客满,若每晚收费每提高2元,便减少10张客床租出,为了获得最大利润,每床每晚收费提高( ).
A.2元 B.4元 C.6元 D.8元
7.函数有两个零点,则( ).
8.某企业生产总值的月平均增长率为P,则年平均增长率为( )
9.如图所示,阴影部分的面积S是h的函数(0≤h≤H),则该函数的图象是哪一个( ).
10.某商店计划投入资金20万元经销甲或乙两种商品,已知经销甲商品与乙商品所获得的利润分别为P(万元)和Q(万元),且它们与投入资金x(万元)的关系是;若不管资金如何投放,经销这两种商品或其中的一种商品所获得的纯利润总不少于5万元,则a的最小值应为( ).
二、填空题(本大题共5小题,每小题7分,共35分.把答案填在题中的横线上)
11.1992年底,世界人口已达到54.8亿,若世界人口的年平均增长率为x,2008年底人口数为y亿,那么y与x之间的关系式为 .
12.函数f(x)=x+b有一个零点2,那么函数的零点是 .
13.用二分法求方程在区间(2,4)上实数根时,取中点则下一个有根区间是 .
14.芒幕电子公司7年来,生产VCD总产量y(万台,即前t年年产量的和)与时间t(年)的函数关系式如图所示,下列4种说法:
①前3年中,产量增长的速度越来越快;
②前3年中,产量增长的速度越来越慢;
③第3年后,这种产品停止生产;
④第3年后,年产量保持为100万台.
其中正确的说法是 .(把正确说法的序号填上即可)
15.函数的零点均是正数,则实数m的取值范围是 .
三、解答题(本大题共4小题,共45分,解答时应写出文字说明、证明过程或演算步骤)
16.(10分)求方程的近似解(精确度为0.1).
17.(10分)将长度为1的铁丝分成两段,分别围成一个正方形和一个圆形,要使正方形与圆的面积之和最小,正方形的周长应为多少?
18.(12分)某影院共有1000个座位,票价不分等次.根据该影院的经营经验,当每张票价不超过10元时,票可全部售出,当每张票价高于10元时,每提高1元,将有30张票不能售出.为了获得更好的收益,需给影院定一个合适的票价,应符合的基本条件是:①为方便找零和算账,票价定为1元的整数倍;②影院放映一场电影的成本费用支出为5 750元,票房收入必须高于成本支出,用x(元)表示每张票价,用y(元)表示该影院放映一场的净收入(除去成本费用支出后的收入).
(1)用y表示为x的函数,并求其定义域;
(2)试问在符合基本条件的前提下,每张票价定为多少元时,放映一场的净收入最多?
19.(13分)以x为自变量的二次函数中,m是不小于零的整数,它的图象与x轴交于点A和点B,点A在原点左边,点B在原点右边.
(1)求这个二次函数的解析式;
(2)一次函数y=kx+b的图象经过点A,与这个二次函数的图象交于点C,且.求一次函数的解析式.
参考答案:
1.B
2.B【提示】计算得,则有
3.C
4.D【提示】抛物线开口向下,a<0,又对称轴在y轴右侧,
,b与a异号,b>0,抛物线与y轴交于负半轴,c<0,A正确.抛物线与x轴没有交点,B正确.抛物线全落在x轴下方,不论x取何值,y均小于O,故x=l时,y=a+b+c<0,C正确.x=-1时,y=a-b+c<0,D不正确.
5.D
6.C【提示】设每床每晚收费提高x元,则总收入y与x之间的关系为
所以当x=4,x=6时,y都取最大,结合实际,应选C.
7.B【提示】令由题意即要求两函数图象有两交点,利用数形结合思想,作出两函数图象,得k>0.
8.C【提示】可以由头年1月到第二年1月份来计算.
9.C【提示】当时,对应阴影部分的面积小于整个半圆面积的一半,且随着h的增大,S随之减小,故排除A、B、D,选择C.
10.A【提示】总利润y是一关于x的函数,利用函数值不小于5,可确定a的不等式,找出a的最小值,
设投放x万元经销甲商品,则经销乙商品投放(20 - x)万元,总利润
则即对恒成立,
而的最大值为,且x =20时,
也成立,故应选A.
11.【提示】1年后,世界人口数为54.8(1+x);
2年后,世界人口数为
3年后,世界人口数为
……
16年后即2008年底,世界人口数
12.【提示】由题意得2+b =0,即b= -2,则即函数的零点是
13.(2,3)【提示】设则有,则下一个有根区间是(2,3).
14.②③【提示】在区间[0,3]上,函数图象越来越远离y轴,则前3年中,产量增长的速度越来越慢,则①错,②正确;在区间(3,7]上,函数图象是平行于x轴的线段,说明没有变化,所以第3年后,这种产品停止生产,则③正确,④错误.
15.(0,1]【提示】设是函数f(x)的零点,
则有即’解得
16.解:令
函数f(x)的正零点在区间(1,2)内.
取(1,2)中点
取(1,1.5)中点
取(1. 25,1.5)中点
取(l. 375,1.5)中点
取(1.437 5,1.5).
方程的近似解为x=1.5.
【提示】转化为求函数的零点,确定函数零点所在的区间,用二分法求其近似解.
17.解:设正方形周长为x时,正方形与圆的面积之和为S.
则正方形边长为,圆周长为1 -x,圆半径为
则
当时,S有最小值,
此时正方形的周长为
【提示】建立函数模型,转化为求函数的最值.
18.解:(1)由题意知当x≤10时,y=1 000x -5 750.
当x>10时,
由解之得:
又所求函数表达式为
其定义域为.
(2)当时,x=10时,
当N)时
时,
每张票价为22元时净收入最多.
19.解:(1)抛物线与x轴有两个交点,关于x的方程有两个不相等的实数根,,解得m<2.
又m为不小于零的整数,m=0或1.
又抛物线与x轴的这两个交点,一个在原点的左边,另一个在原点的右边.
,即
当m=0时,,符合题意,当时,,不符合题意,应舍去.
只能取m=0.原二次函数的解析式为
即
(2)由(1)得A(1,0)、B(3,0),AB=4.
设点C的坐标为,则
又抛物线的开口向下,顶点坐标是(1,4).即抛物线上在x轴上方的任何一点的纵坐标都不能大于4.
点C在抛物线x轴下方的部分上,
,解得或
点C的坐标是(-2,-5)或(4,-5).
一次函数解析式为y= kx+b. ①
将A(1,0)、C(2,5)代入①,
得解得
将A(-1,0)、C(4,-5)代入①,得
解得
故所求一次函数解析式为
