2020--2021学年北师大版数学八年级下册第一章三角形的证明同步课时作业 [范围1.1_1.2](word版含答案)
文档属性
| 名称 | 2020--2021学年北师大版数学八年级下册第一章三角形的证明同步课时作业 [范围1.1_1.2](word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 142.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 10:47:31 | ||
图片预览




文档简介
1.1~1.2
一、选择题
1.如果等腰三角形的一个角是80°,那么它的底角是
( )
A.50°
B.50°或20°
C.80°或20°
D.80°或50°
2.如果直角三角形的一个锐角∠A是另一个锐角∠B的3倍,那么∠B的度数是
( )
A.22.5°
B.45°
C.67.5°
D.135°
3.如图K-6-13,在△ABC中,∠C=90°,∠B=30°,AC=3.若P是BC边上任意一点,则AP的长不可能是
( )
图K-6-13
A.7
B.5.3
C.4.8
D.3.5
4.已知下列命题:①若>1,则a>b;②若a+b=0,则|a|=|b|;③等边三角形的三个内角都相等;④底角相等的两个等腰三角形全等.其中原命题与逆命题均为真命题的个数是
( )
A.1
B.2
C.3
D.4
5.如图K-6-14,AB⊥CD,且AB=CD,E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=5,BF=3,EF=2,则AD的长为
( )
图K-6-14
A.4
B.5
C.6
D.7
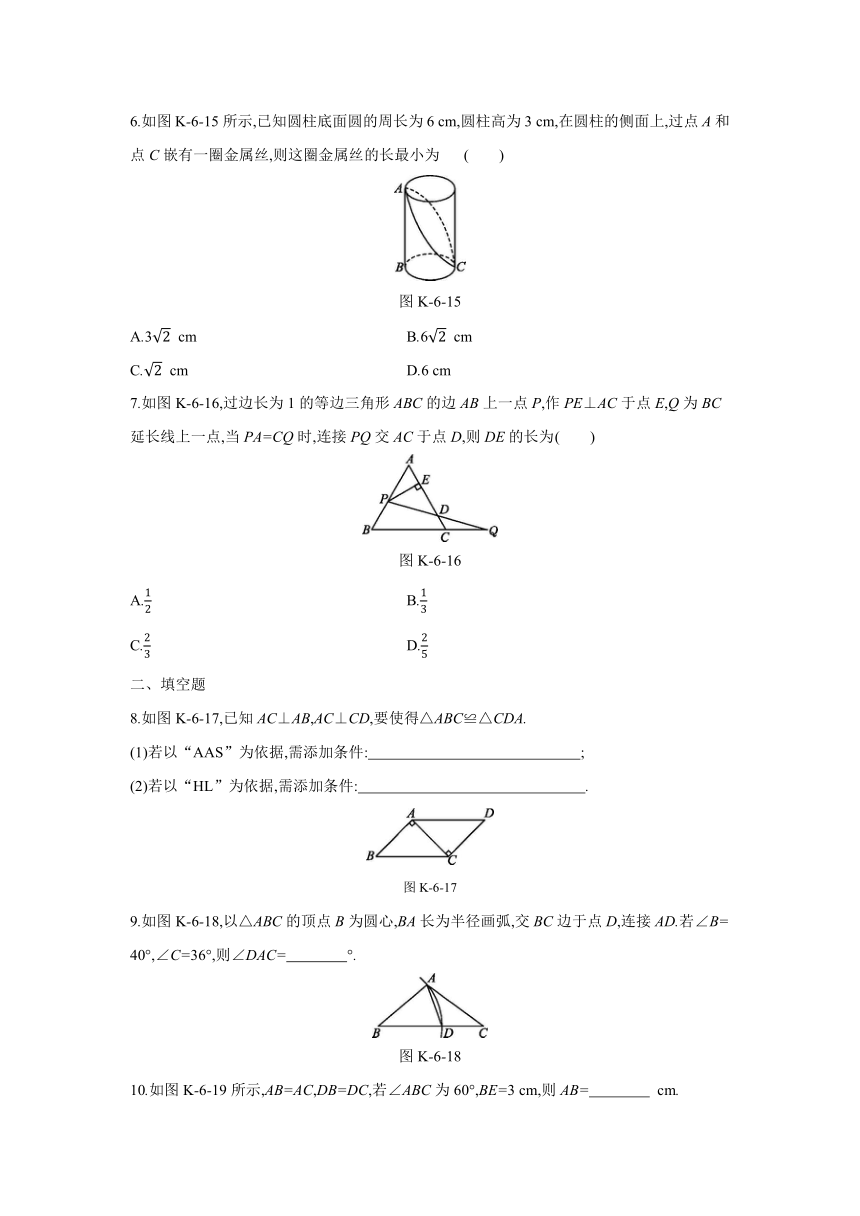
6.如图K-6-15所示,已知圆柱底面圆的周长为6
cm,圆柱高为3
cm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的长最小为
( )
图K-6-15
A.3
cm
B.6
cm
C.
cm
D.6
cm
7.如图K-6-16,过边长为1的等边三角形ABC的边AB上一点P,作PE⊥AC于点E,Q为BC延长线上一点,当PA=CQ时,连接PQ交AC于点D,则DE的长为
( )
图K-6-16
A.
B.
C.
D.
二、填空题
8.如图K-6-17,已知AC⊥AB,AC⊥CD,要使得△ABC≌△CDA.
(1)若以“AAS”为依据,需添加条件:
;?
(2)若以“HL”为依据,需添加条件:
.?
图K-6-17
9.如图K-6-18,以△ABC的顶点B为圆心,BA长为半径画弧,交BC边于点D,连接AD.若∠B=
40°,∠C=36°,则∠DAC= °.?
图K-6-18
10.如图K-6-19所示,AB=AC,DB=DC,若∠ABC为60°,BE=3
cm,则AB=
cm.?
图K-6-19
11.等腰三角形一腰上的高与另一腰的夹角为45°,则等腰三角形的底角为 .?
三、解答题
12.如图K-6-20,点C,E,B,F在一条直线上,AB⊥CF于点B,DE⊥CF于点E,AC=DF,AB=DE.求证:CE=BF.
图K-6-20
13.如图K-6-21,已知∠AOB=60°,点P在边OA上,点M,N在边OB上.
(1)若∠PNO=60°,求证:△PON是等边三角形;
(2)若PM=PN,OP=12,MN=2,求OM的长度.
图K-6-21
14.在海洋上有一个近似于四边形的岛屿,其平面图如图K-6-22甲,小明据此构造出该岛的一个数学模型(如图乙中的四边形ABCD),AC是四边形岛屿上的一条小溪流,其中∠B=90°,
AB=BC=5千米,CD=千米,AD=4千米.
(1)求小溪流AC的长;
(2)求四边形ABCD的面积.(结果保留根号)
图K-6-22
15.如图K-6-23,在Rt△ABC中,∠A=30°,∠ACB=90°,D为AC的中点,E为AB边上一动点,AE=DE,延长ED交BC的延长线于点F.
(1)求证:△BEF是等边三角形;
(2)若AB=12,求DE的长.
图K-6-23
16.如图K-6-24,在△ABC中,∠B=30°,∠C=∠B,AB=2
cm,点P从点B开始以1
cm/s的速度向点C移动,要使△ABP是以AB为腰的等腰三角形,点P的运动时间是多少秒?
图K-6-24
教师详解详析
1.[解析]
D 根据题意,等腰三角形的一个角等于80°,①若这个角是底角,则该等腰三角形的底角的度数是80°;②若这个角是顶角,设等腰三角形的底角是x°,则2x+80=180,解得x=50,即该等腰三角形的底角的度数是50°.故选D.
2.[解析]
A 设∠B=x°,则∠A=3x°,由直角三角形的性质可得∠A+∠B=90°,∴x+3x=90,解得x=22.5,∴∠B=22.5°.故选A.
3.[解析]
A ∵∠C=90°,∠B=30°,∴AB=2AC=6,∴3≤AP≤6.故选A.
4.[解析]
A ①当b<0时,如果>1,那么a②若a+b=0,则|a|=|b|,但是若|a|=|b|,则a+b=0或a=b,∴原命题是真命题,逆命题是假命题,故②不符合题意;
③等边三角形的三个内角都相等,是真命题,逆命题也是真命题,∴③符合题意;
④底角相等的两个等腰三角形不一定全等,
∴原命题是假命题,故④不符合题意.
故选A.
5.[答案]
C
6.[解析]
B 如图,把圆柱的侧面展开,得到长方形,则这圈金属丝的长最小为2AC的长度.∵圆柱底面圆的周长为6
cm,圆柱高为3
cm,
∴AB=3
cm,BC=BC'=3
cm,∴AC2=32+32=18,∴AC=3
cm,∴这圈金属丝的长最小为2AC=6
cm.故选B.
7.[解析]
A 过点P作PF∥BC交AC于点F,如图所示.
∵PF∥BC,△ABC是等边三角形,∴∠PFD=∠QCD,∠APF=∠ABC=60°,∠AFP=∠ACB=60°,∴△APF是等边三角形,∴PA=FP=AF.
∵PE⊥AC,∴AE=EF.
∵PA=FP,PA=CQ,∴FP=CQ.
在△PFD和△QCD中,∵∠PFD=∠QCD,∠PDF=∠QDC,FP=CQ,∴△PFD≌△QCD(AAS),∴FD=CD.∵AE=EF,∴EF+FD=AE+CD=AC,∴DE=AC.
∵AC=1,∴DE=.故选A.
8.[答案]
(1)∠B=∠D (2)BC=DA
9.[答案]
34
[解析]
∵∠B=40°,∠C=36°,
∴∠BAC=180°-∠B-∠C=104°.
∵AB=BD,
∴∠BAD=∠ADB=(180°-∠B)÷2=70°,
∴∠DAC=∠BAC-∠BAD=34°.故答案为34.
10.[答案]
6
[解析]
在△ABD和△ACD中,∵AB=AC,DB=DC,AD=AD,∴△ABD≌△ACD,∴∠BAD=∠CAD.又∵AB=AC,∴BE=CE=3
cm,∴BC=6
cm.∵AB=AC,∠ABC=60°,∴△ABC为等边三角形,∴AB=BC=6
cm.故答案为6.
11.[答案]
67.5°或22.5°
[解析]
有两种情况:
(1)如图①:
若△ABC是锐角三角形,过点B作BD⊥AC于点D,则∠ADB=90°.已知∠ABD=45°,∴∠A=90°-45°=45°.∵AB=AC,∴∠ABC=∠C=×(180°-45°)=67.5°;
(2)如图②:
若△EFG是钝角三角形,过点F作FH⊥GE交GE的延长线于点H,则∠FHE=90°.
已知∠HFE=45°,∴∠HEF=90°-45°=45°,
∴∠FEG=180°-45°=135°.
∵EF=EG,
∴∠EFG=∠G=×(180°-135°)=22.5°.故答案为67.5°或22.5°.
12.证明:∵AB⊥CF,DE⊥CF,
∴∠ABC=∠DEF=90°.
在Rt△ABC和Rt△DEF中,
∵AC=DF,AB=DE,
∴Rt△ABC≌Rt△DEF(HL),∴BC=EF,
∴BC-BE=EF-BE,即CE=BF.
13.解:(1)证明:∵∠AOB=60°,∠PNO=60°,
∴∠OPN=60°,
∴∠PON=∠PNO=∠OPN,
∴△PON是等边三角形.
(2)过点P作PH⊥MN于点H,如图.
∵PM=PN,
∴MH=NH=MN=1.
在Rt△POH中,
∵∠POH=60°,
∴∠OPH=30°,
∴OH=OP=×12=6,
∴OM=OH-MH=6-1=5.
14.解:(1)∵∠B=90°,AB=BC=5千米,
∴AC===5(千米).
(2)∵AC2=(5)2=50,CD2+AD2=()2+(4)2=50,
∴AC2=CD2+AD2,则∠D=90°,
∴S四边形ABCD=S△ABC+S△ACD=×5×5+××4=+2千米2.
15.解:(1)证明:∵∠A=30°,∠ACB=90°,
∴∠B=60°.
∵AE=DE,∴∠ADE=∠A=30°,
∴∠BEF=∠A+∠ADE=60°,
∴∠F=180°-∠B-∠BEF=180°-60°-60°=60°,
∴∠B=∠BEF=∠F,
∴△BEF是等边三角形.
(2)如图,在EF上截取FG=CF,连接CG.
∵∠F=60°,∴△CFG为等边三角形,
∴∠FGC=∠F=∠BEF=60°,
∴∠AED=∠CGD.
∵D为AC的中点,∴AD=CD.
在△ADE和△CDG中,
∵∠ADE=∠CDG,∠AED=∠CGD,AD=CD,
∴△ADE≌△CDG(AAS),
∴AE=CG.
设AE=x,则BE=12-x,
∴CF=CG=AE=x.
易知BC=AB=6,
∴BF=6+x.
∵△BEF是等边三角形,∴BE=BF,
∴12-x=6+x,
解得x=3,∴DE=AE=3.
16.解:(1)若AB=AP,过点A作AD⊥BC于点D.
∵∠C=∠B,∴AB=AC,则此时点P与点C重合.
∵AD⊥BC,∴BD=CD.
∵∠B=30°,AB=2
cm,
∴AD=
cm,
∴BD==3
cm,
∴BC=6
cm,即点P的运动时间是6
s;
(2)若AB=BP.∵AB=2
cm,
∴BP=2
cm,∴点P的运动时间为2
s.
综上可知,要使△ABP是以AB为腰的等腰三角形,点P的运动时间是2
s或6
s.
一、选择题
1.如果等腰三角形的一个角是80°,那么它的底角是
( )
A.50°
B.50°或20°
C.80°或20°
D.80°或50°
2.如果直角三角形的一个锐角∠A是另一个锐角∠B的3倍,那么∠B的度数是
( )
A.22.5°
B.45°
C.67.5°
D.135°
3.如图K-6-13,在△ABC中,∠C=90°,∠B=30°,AC=3.若P是BC边上任意一点,则AP的长不可能是
( )
图K-6-13
A.7
B.5.3
C.4.8
D.3.5
4.已知下列命题:①若>1,则a>b;②若a+b=0,则|a|=|b|;③等边三角形的三个内角都相等;④底角相等的两个等腰三角形全等.其中原命题与逆命题均为真命题的个数是
( )
A.1
B.2
C.3
D.4
5.如图K-6-14,AB⊥CD,且AB=CD,E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=5,BF=3,EF=2,则AD的长为
( )
图K-6-14
A.4
B.5
C.6
D.7
6.如图K-6-15所示,已知圆柱底面圆的周长为6
cm,圆柱高为3
cm,在圆柱的侧面上,过点A和点C嵌有一圈金属丝,则这圈金属丝的长最小为
( )
图K-6-15
A.3
cm
B.6
cm
C.
cm
D.6
cm
7.如图K-6-16,过边长为1的等边三角形ABC的边AB上一点P,作PE⊥AC于点E,Q为BC延长线上一点,当PA=CQ时,连接PQ交AC于点D,则DE的长为
( )
图K-6-16
A.
B.
C.
D.
二、填空题
8.如图K-6-17,已知AC⊥AB,AC⊥CD,要使得△ABC≌△CDA.
(1)若以“AAS”为依据,需添加条件:
;?
(2)若以“HL”为依据,需添加条件:
.?
图K-6-17
9.如图K-6-18,以△ABC的顶点B为圆心,BA长为半径画弧,交BC边于点D,连接AD.若∠B=
40°,∠C=36°,则∠DAC= °.?
图K-6-18
10.如图K-6-19所示,AB=AC,DB=DC,若∠ABC为60°,BE=3
cm,则AB=
cm.?
图K-6-19
11.等腰三角形一腰上的高与另一腰的夹角为45°,则等腰三角形的底角为 .?
三、解答题
12.如图K-6-20,点C,E,B,F在一条直线上,AB⊥CF于点B,DE⊥CF于点E,AC=DF,AB=DE.求证:CE=BF.
图K-6-20
13.如图K-6-21,已知∠AOB=60°,点P在边OA上,点M,N在边OB上.
(1)若∠PNO=60°,求证:△PON是等边三角形;
(2)若PM=PN,OP=12,MN=2,求OM的长度.
图K-6-21
14.在海洋上有一个近似于四边形的岛屿,其平面图如图K-6-22甲,小明据此构造出该岛的一个数学模型(如图乙中的四边形ABCD),AC是四边形岛屿上的一条小溪流,其中∠B=90°,
AB=BC=5千米,CD=千米,AD=4千米.
(1)求小溪流AC的长;
(2)求四边形ABCD的面积.(结果保留根号)
图K-6-22
15.如图K-6-23,在Rt△ABC中,∠A=30°,∠ACB=90°,D为AC的中点,E为AB边上一动点,AE=DE,延长ED交BC的延长线于点F.
(1)求证:△BEF是等边三角形;
(2)若AB=12,求DE的长.
图K-6-23
16.如图K-6-24,在△ABC中,∠B=30°,∠C=∠B,AB=2
cm,点P从点B开始以1
cm/s的速度向点C移动,要使△ABP是以AB为腰的等腰三角形,点P的运动时间是多少秒?
图K-6-24
教师详解详析
1.[解析]
D 根据题意,等腰三角形的一个角等于80°,①若这个角是底角,则该等腰三角形的底角的度数是80°;②若这个角是顶角,设等腰三角形的底角是x°,则2x+80=180,解得x=50,即该等腰三角形的底角的度数是50°.故选D.
2.[解析]
A 设∠B=x°,则∠A=3x°,由直角三角形的性质可得∠A+∠B=90°,∴x+3x=90,解得x=22.5,∴∠B=22.5°.故选A.
3.[解析]
A ∵∠C=90°,∠B=30°,∴AB=2AC=6,∴3≤AP≤6.故选A.
4.[解析]
A ①当b<0时,如果>1,那么a
③等边三角形的三个内角都相等,是真命题,逆命题也是真命题,∴③符合题意;
④底角相等的两个等腰三角形不一定全等,
∴原命题是假命题,故④不符合题意.
故选A.
5.[答案]
C
6.[解析]
B 如图,把圆柱的侧面展开,得到长方形,则这圈金属丝的长最小为2AC的长度.∵圆柱底面圆的周长为6
cm,圆柱高为3
cm,
∴AB=3
cm,BC=BC'=3
cm,∴AC2=32+32=18,∴AC=3
cm,∴这圈金属丝的长最小为2AC=6
cm.故选B.
7.[解析]
A 过点P作PF∥BC交AC于点F,如图所示.
∵PF∥BC,△ABC是等边三角形,∴∠PFD=∠QCD,∠APF=∠ABC=60°,∠AFP=∠ACB=60°,∴△APF是等边三角形,∴PA=FP=AF.
∵PE⊥AC,∴AE=EF.
∵PA=FP,PA=CQ,∴FP=CQ.
在△PFD和△QCD中,∵∠PFD=∠QCD,∠PDF=∠QDC,FP=CQ,∴△PFD≌△QCD(AAS),∴FD=CD.∵AE=EF,∴EF+FD=AE+CD=AC,∴DE=AC.
∵AC=1,∴DE=.故选A.
8.[答案]
(1)∠B=∠D (2)BC=DA
9.[答案]
34
[解析]
∵∠B=40°,∠C=36°,
∴∠BAC=180°-∠B-∠C=104°.
∵AB=BD,
∴∠BAD=∠ADB=(180°-∠B)÷2=70°,
∴∠DAC=∠BAC-∠BAD=34°.故答案为34.
10.[答案]
6
[解析]
在△ABD和△ACD中,∵AB=AC,DB=DC,AD=AD,∴△ABD≌△ACD,∴∠BAD=∠CAD.又∵AB=AC,∴BE=CE=3
cm,∴BC=6
cm.∵AB=AC,∠ABC=60°,∴△ABC为等边三角形,∴AB=BC=6
cm.故答案为6.
11.[答案]
67.5°或22.5°
[解析]
有两种情况:
(1)如图①:
若△ABC是锐角三角形,过点B作BD⊥AC于点D,则∠ADB=90°.已知∠ABD=45°,∴∠A=90°-45°=45°.∵AB=AC,∴∠ABC=∠C=×(180°-45°)=67.5°;
(2)如图②:
若△EFG是钝角三角形,过点F作FH⊥GE交GE的延长线于点H,则∠FHE=90°.
已知∠HFE=45°,∴∠HEF=90°-45°=45°,
∴∠FEG=180°-45°=135°.
∵EF=EG,
∴∠EFG=∠G=×(180°-135°)=22.5°.故答案为67.5°或22.5°.
12.证明:∵AB⊥CF,DE⊥CF,
∴∠ABC=∠DEF=90°.
在Rt△ABC和Rt△DEF中,
∵AC=DF,AB=DE,
∴Rt△ABC≌Rt△DEF(HL),∴BC=EF,
∴BC-BE=EF-BE,即CE=BF.
13.解:(1)证明:∵∠AOB=60°,∠PNO=60°,
∴∠OPN=60°,
∴∠PON=∠PNO=∠OPN,
∴△PON是等边三角形.
(2)过点P作PH⊥MN于点H,如图.
∵PM=PN,
∴MH=NH=MN=1.
在Rt△POH中,
∵∠POH=60°,
∴∠OPH=30°,
∴OH=OP=×12=6,
∴OM=OH-MH=6-1=5.
14.解:(1)∵∠B=90°,AB=BC=5千米,
∴AC===5(千米).
(2)∵AC2=(5)2=50,CD2+AD2=()2+(4)2=50,
∴AC2=CD2+AD2,则∠D=90°,
∴S四边形ABCD=S△ABC+S△ACD=×5×5+××4=+2千米2.
15.解:(1)证明:∵∠A=30°,∠ACB=90°,
∴∠B=60°.
∵AE=DE,∴∠ADE=∠A=30°,
∴∠BEF=∠A+∠ADE=60°,
∴∠F=180°-∠B-∠BEF=180°-60°-60°=60°,
∴∠B=∠BEF=∠F,
∴△BEF是等边三角形.
(2)如图,在EF上截取FG=CF,连接CG.
∵∠F=60°,∴△CFG为等边三角形,
∴∠FGC=∠F=∠BEF=60°,
∴∠AED=∠CGD.
∵D为AC的中点,∴AD=CD.
在△ADE和△CDG中,
∵∠ADE=∠CDG,∠AED=∠CGD,AD=CD,
∴△ADE≌△CDG(AAS),
∴AE=CG.
设AE=x,则BE=12-x,
∴CF=CG=AE=x.
易知BC=AB=6,
∴BF=6+x.
∵△BEF是等边三角形,∴BE=BF,
∴12-x=6+x,
解得x=3,∴DE=AE=3.
16.解:(1)若AB=AP,过点A作AD⊥BC于点D.
∵∠C=∠B,∴AB=AC,则此时点P与点C重合.
∵AD⊥BC,∴BD=CD.
∵∠B=30°,AB=2
cm,
∴AD=
cm,
∴BD==3
cm,
∴BC=6
cm,即点P的运动时间是6
s;
(2)若AB=BP.∵AB=2
cm,
∴BP=2
cm,∴点P的运动时间为2
s.
综上可知,要使△ABP是以AB为腰的等腰三角形,点P的运动时间是2
s或6
s.
