2020—2021学年 北师大版七年级数学下册第4章三角形高频热点专题提升训练(word解析版)
文档属性
| 名称 | 2020—2021学年 北师大版七年级数学下册第4章三角形高频热点专题提升训练(word解析版) |

|
|
| 格式 | doc | ||
| 文件大小 | 200.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 00:00:00 | ||
图片预览

文档简介
2021年度北师大版七年级数学下册《第4章三角形》高频热点专题提升训练(附答案)
1.如果三角形的两条边长分别是8厘米、6厘米,那么第三边的长不可能是( )
A.9厘米 B.4厘米 C.3厘米 D.2厘米
2.如果一个三角形的两个外角之和为270°,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
3.画△ABC的边BC上的高,正确的是( )
A.B.C.D.
4.如图,△ABC中,AB=15,BC=9,BD是AC边上的中线,若△ABD的周长为30,则△BCD的周长是( )
A.20 B.24 C.26 D.28
5.如图,△ABC的高CD、BE相交于点O,如果∠A=60°,那么∠BOC的大小为( )
A.60° B.100° C.120° D.130°
6.如图,将△ABC沿着DE翻折,使B点与B′点重合,若∠1+∠2=80°,则∠B的度数为( )
A.20° B.30° C.40° D.50°
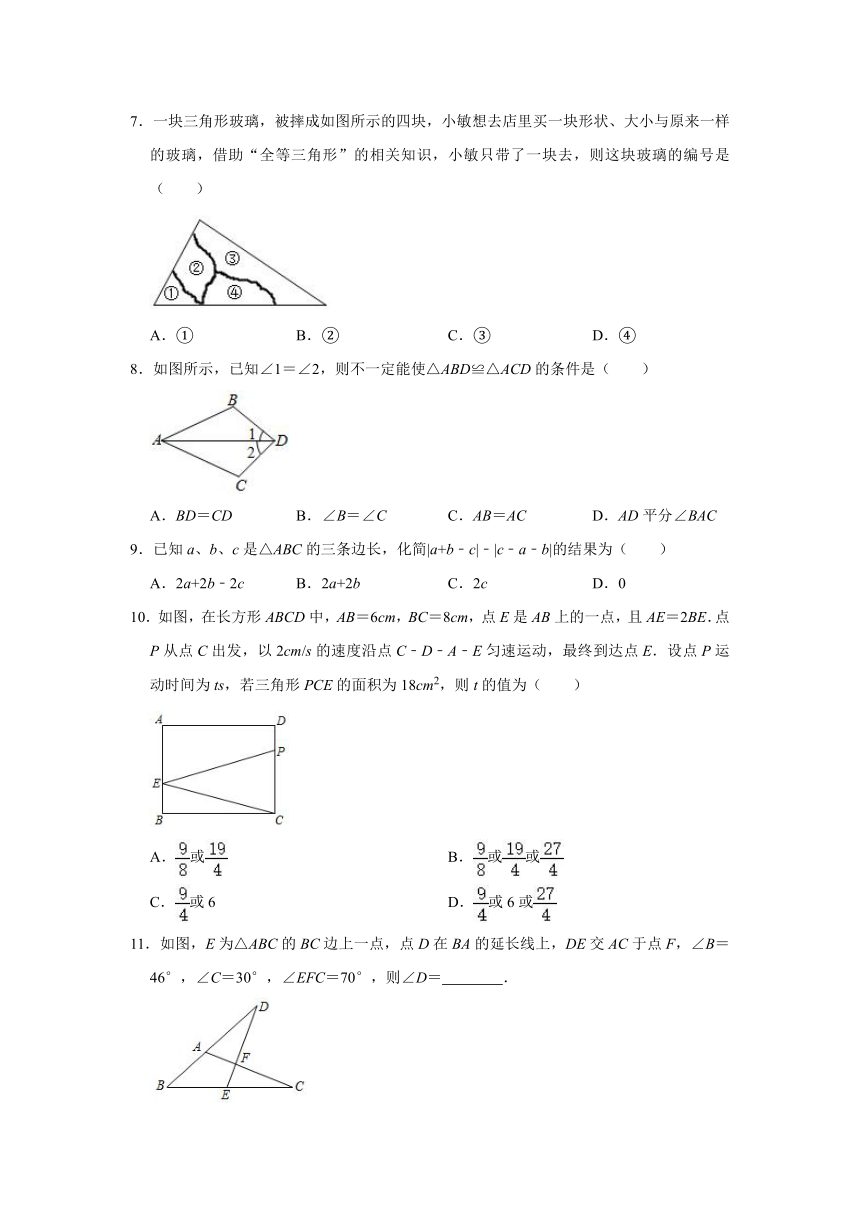
7.一块三角形玻璃,被摔成如图所示的四块,小敏想去店里买一块形状、大小与原来一样的玻璃,借助“全等三角形”的相关知识,小敏只带了一块去,则这块玻璃的编号是( )
A.① B.② C.③ D.④
8.如图所示,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
A.BD=CD B.∠B=∠C C.AB=AC D.AD平分∠BAC
9.已知a、b、c是△ABC的三条边长,化简|a+b﹣c|﹣|c﹣a﹣b|的结果为( )
A.2a+2b﹣2c B.2a+2b C.2c D.0
10.如图,在长方形ABCD中,AB=6cm,BC=8cm,点E是AB上的一点,且AE=2BE.点P从点C出发,以2cm/s的速度沿点C﹣D﹣A﹣E匀速运动,最终到达点E.设点P运动时间为ts,若三角形PCE的面积为18cm2,则t的值为( )
A.或 B.或或
C.或6 D.或6或
11.如图,E为△ABC的BC边上一点,点D在BA的延长线上,DE交AC于点F,∠B=46°,∠C=30°,∠EFC=70°,则∠D= .
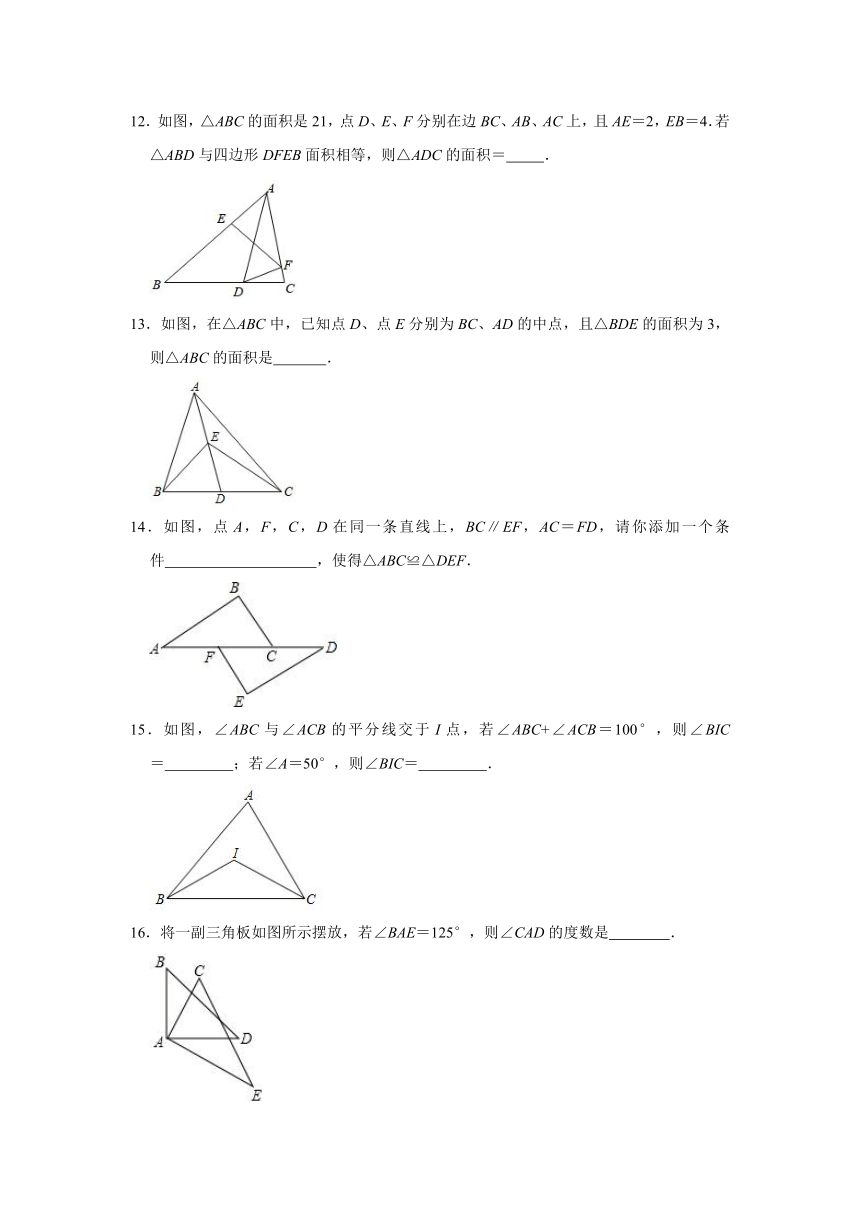
12.如图,△ABC的面积是21,点D、E、F分别在边BC、AB、AC上,且AE=2,EB=4.若△ABD与四边形DFEB面积相等,则△ADC的面积= .
13.如图,在△ABC中,已知点D、点E分别为BC、AD的中点,且△BDE的面积为3,则△ABC的面积是 .
14.如图,点A,F,C,D在同一条直线上,BC∥EF,AC=FD,请你添加一个条件 ,使得△ABC≌△DEF.
15.如图,∠ABC与∠ACB的平分线交于I点,若∠ABC+∠ACB=100°,则∠BIC= ;若∠A=50°,则∠BIC= .
16.将一副三角板如图所示摆放,若∠BAE=125°,则∠CAD的度数是 .
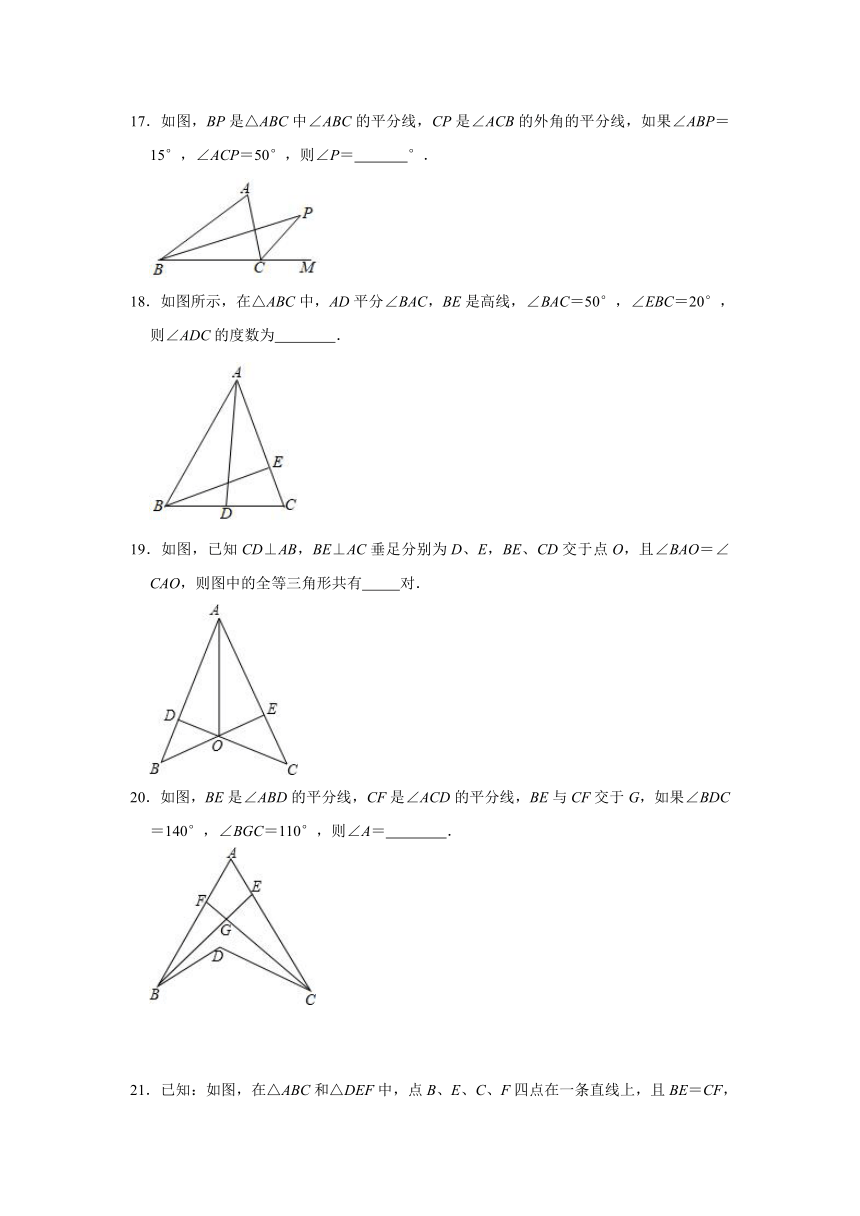
17.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=15°,∠ACP=50°,则∠P= °.
18.如图所示,在△ABC中,AD平分∠BAC,BE是高线,∠BAC=50°,∠EBC=20°,则∠ADC的度数为 .
19.如图,已知CD⊥AB,BE⊥AC垂足分别为D、E,BE、CD交于点O,且∠BAO=∠CAO,则图中的全等三角形共有 对.
20.如图,BE是∠ABD的平分线,CF是∠ACD的平分线,BE与CF交于G,如果∠BDC=140°,∠BGC=110°,则∠A= .
21.已知:如图,在△ABC和△DEF中,点B、E、C、F四点在一条直线上,且BE=CF,AB=DE,∠B=∠DEF.
求证:△ABC≌△DEF.
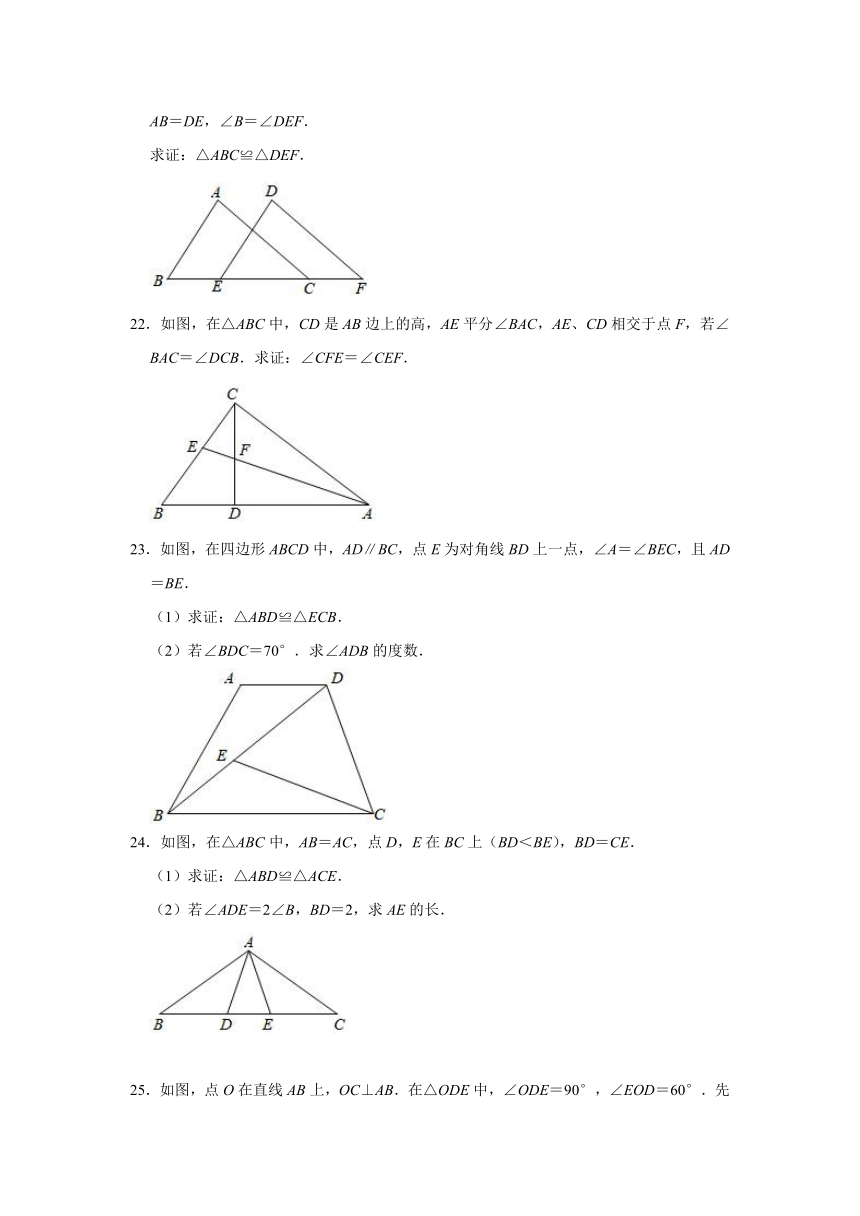
22.如图,在△ABC中,CD是AB边上的高,AE平分∠BAC,AE、CD相交于点F,若∠BAC=∠DCB.求证:∠CFE=∠CEF.
23.如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD=BE.
(1)求证:△ABD≌△ECB.
(2)若∠BDC=70°.求∠ADB的度数.
24.如图,在△ABC中,AB=AC,点D,E在BC上(BD<BE),BD=CE.
(1)求证:△ABD≌△ACE.
(2)若∠ADE=2∠B,BD=2,求AE的长.
25.如图,点O在直线AB上,OC⊥AB.在△ODE中,∠ODE=90°,∠EOD=60°.先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.
(1)当OD在OA与OC之间,且∠COD=25°时,则∠AOE= °.
(2)试探索:在△ODE旋转过程中,∠AOD与∠COE大小的差是否发生变化?若不变,请求出这个差值;若变化,请说明理由;
(3)在△ODE的旋转过程中,若∠AOE=7∠COD,试求∠AOE的大小.
26.如图,△ABC中,AB=AC,AD是BC边上的高,CE是AB边上的高,AE=CE.
求证:(1)△AEF≌△CEB;
(2)AF=2CD.
27.如图,点D是线段CE上一点,且AB=AC,AD=AE,∠BAC=∠DAE.
(1)求证:BD=CE;
(2)若∠B=40°,∠E=80°,求∠CAD的度数.
参考答案
1.解:设第三边为a,
根据三角形的三边关系可得:8﹣6<a<8+6,
解得:2<a<14.
故第三边不可能是2,
故选:D.
2.解:如图:
∵∠EAC+∠FCA=270°,
∴∠BAC+∠ACB=180°﹣∠EAC+180°﹣∠FCA=360°﹣(∠EAC+∠FCA)=90°,
∴∠B=180°﹣(∠BAC+∠ACB)=90°,
即△ABC是直角三角形.
故选:B.
3.解:A.此图形中AD是BC边上的高,符合题意;
B.此图形中CD不是BC边上的高,不符合题意;
C.此图形中CD是AB边上的高,不符合题意;
D.此图形中AD是AB边上的高,不符合题意;
故选:A.
4.解:∵BD是AC边上的中线,
∴AD=CD.
∵△ABD的周长为30,
∴AB+BD+AD=30.
∴BD+AD=30﹣AB=30﹣15=15.
∴△BCD的周长为BC+CD+BD=BC+AD+BD=9+15=24.
故选:B.
5.解:如图,
∵CD、BE均为△ABC的高,
∴∠BEC=∠ADC=90°,
∵∠A=60°,
∴∠OCE=180°﹣∠ADC﹣∠A=180°﹣90°﹣60°=30°,
则∠BOC=∠BEC+∠OCE=90°+30°=120°.
故选:C.
6.解:由翻折可知:∠BED=∠B'ED,∠BDE=∠B'DE,
∵∠1+∠BED+∠B'ED=180°,∠2+∠BDE+∠B'DE=180°,
∴∠1+2∠BED+∠2+2∠BDE=360°,
∵∠1+∠2=80°,
∴2∠BED+2∠BDE=280°,
∴∠BED+∠BDE=140°,
∵∠BED+∠BDE+∠B=180°,
∴∠B=180°﹣140°=40°.
故选:C.
7.解:因为第③块中有完整的两个角以及他们的夹边,利用ASA易证三角形全等,故应带第3块.
故选:C.
8.解:A.BD=CD,∠1=∠2,AD=AD,符合全等三角形的判定定理SAS,能推出△ABD≌△ACD,故本选项不符合题意;
B.∠B=∠C,∠1=∠2,AD=AD,符合全等三角形的判定定理AAS,能推出△ABD≌△ACD,故本选项不符合题意;
C.AB=AC,AD=AD,∠1=∠2,不符合全等三角形的判定定理,不能推出△ABD≌△ACD,故本选项符合题意;
D.∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵AD=AD,∠1=∠2,
∴△ABD≌△ACD(ASA),故本选项不符合题意;
故选:C.
9.解:根据三角形的三边关系,两边之和大于第三边,
得a+b﹣c>0,c﹣a﹣b<0,
故|a+b﹣c|﹣|c﹣a﹣b|=a+b﹣c+c﹣a﹣b=0.
故选:D.
10.解:如图1,当点P在CD上,即0<t≤3时,
∵四边形ABCD是矩形,
∴AB=CD=6cm,AD=BC=8cm.
∵CP=2t(cm),
∴S△PCE=×2t×8=18,
∴t=;
如图2,当点P在BC上,即3<t≤7时,
∵AE=2BE,
∴AE=AB=4.
∵DP=2t﹣6,AP=8﹣(2t﹣6)=14﹣2t.
∴S△PCE=×(4+6)×8﹣(2t﹣6)×6﹣(14﹣2t)×4=18,
解得:t=6;
当点P在AE上,即7<t≤9时,
PE=18﹣2t.
∴S△APE=(18﹣2t)×8=18,
解得:t=<7(舍去).
综上所述,当t=或6时△APE的面积会等于18.
故选:C.
11.解:∵∠B=46°,∠C=30°,
∴∠DAC=∠B+∠C=76°,
∵∠EFC=70°,
∴∠AFD=70°,
∴∠D=180°﹣∠DAC﹣∠AFD=34°,
故答案为:34°.
12.解:如图,连接CE,AD交EF于点G
∵S△ABD=S四边形DFEB,
∴S△AEG=S△DFG,
∴S△AEG+S△AFG=S△DFG+S△AFG,
∴S△AEF=S△ADF,
设△ACE的边AC上的高为h1,
∵S△AEF=?AF?h1,S△AEC=?AC?h1,
设△ACD的边AC上的高为h2,
∵S△ADF=?AF?h2,S△ADC=?AC?h2,
∵S△AEF=S△ADF,
∴h1=h2,
∴S△AEC=S△ADC,
∵AE=2,EB=4,
∴S△AEC=S△BEC=S△ABC,
∵S△ABC=21,
∴S△AEC=7,
∴S△ADC=7.
故答案为:7.
13.解:∵点E为AD的中点,△BDE的面积为3,
∴△ABD的面积为3×2=6,
∵点D为BC的中点,
∴△ABC的面积为6×2=12.
故答案为:12.
14.解:∵BC∥EF,
∴∠BCA=∠EFD,
若添加BC=EF,且AC=FD,由“SAS”可证△ABC≌△DEF;
若添加∠B=∠E,且AC=FD,由“AAS”可证△ABC≌△DEF;
若添加∠A=∠D,且AC=FD,由“ASA”可证△ABC≌△DEF;
故答案为:BC=EF或∠B=∠E或∠A=∠D(答案不唯一).
15.解:∵BI平分∠ABC,CI平分∠ACB,
∴∠IBC=∠ABC,∠ICB=∠ACB,
∴∠IBC+∠ICB=(∠ABC+∠ACB)=50°,
∴∠BIC=180°﹣(∠IBC+∠ICB)=130°;
当∠A=50°时,∠ABC+∠ACB=180°﹣∠A=130°,
∴∠IBC+∠ICB=(∠ABC+∠ACB)=65°,
∴∠BIC=180°﹣(∠IBC+∠ICB)=115°.
故答案为:130°;115°.
16.解:∵∠BAE=125°,
∴∠DAE=∠BAE﹣∠BAD=125°﹣90°=35°,
∴∠CAD=∠CAE﹣∠DAE=90°﹣35°=55°,
故答案为:55°.
17.解:∵BP是△ABC中∠ABC的平分线,∠ABP=15°,
∴∠CBP=∠ABP=15°,
∵CP是∠ACB的外角的平分线,∠ACP=50°,
∴∠PCM=∠ACP=50°,
∴∠P=∠PCM﹣∠CBP=50°﹣15°=35°,
故答案为:35.
18.解:∵AD平分∠BAC,BE是高,∠BAC=50°,
∴∠BAD=∠BAC=25°,∠ABE=40°.
∵∠EBC=20°,
∴∠ADC=∠ABD+∠BAD=∠ABE+∠EBC+∠BAD=40°+20°+25°=85°.
故答案为:85°.
19.解:∵CD⊥AB,BE⊥AC,
∴∠ADO=∠AEO=90°,
∵AO=AO,∠DAO=∠EAO,
∴△ADO≌△AEO(AAS);
∴OD=OE,AD=AE,
∵∠DOB=∠EOC,∠ODB=∠OEC=90°,
∴△BOD≌△COE(ASA);
∴BD=CE,OB=OC,∠B=∠C;
∵AE=AD,∠DAC=∠CAB,∠ADC=∠AEB=90°;
∴△ADC≌△AEB(ASA);
∵AD=AE,BD=CE;
∴AB=AC;
∵OB=OC,AO=AO;
∴△ABO≌△ACO(SSS).
所以共有四对全等三角形.
故答案为:四.
20.解:连接BC,
∵∠BDC=140°,
∴∠DBC+∠DCB=180°﹣140°=40°,
∵∠BGC=110°,
∴∠GBC+∠GCB=180°﹣110°=70°,
∴∠GBD+∠GCD=70°﹣40°=30°,
∵BE是∠ABD的平分线,CF是∠ACD的平分线,
∴∠ABG+∠ACG=∠GBD+∠GCD=30°,
在△ABC中,∠A=180°﹣40°﹣30°﹣30°=80°.
故答案为:80°.
21.证明:∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(SAS).
22.证明:在△ABC中,CD是高,∠BAC=∠DCB,
∴∠CDA=90°,∠BAC+∠ACD=90°,
∴∠DCB+∠ACD=90°,
∴∠ACB=90°;
∵AE是角平分线,
∴∠CAE=∠BAE,
∵∠FDA=90°,∠ACE=90°,
∴∠DAF+∠AFD=90°,∠CAE+∠CEA=90°,
∴∠AFD=∠CEA,
∵∠AFD=∠CFE,
∴∠CFE=∠CEA,
即∠CFE=∠CEF.
23.证明:(1)∵AD∥BC,
∴∠ADB=∠CBE,
在△ABD和△ECB中,
,
∴△ABD≌△ECB(ASA);
(2)∵△ABD≌△ECB,
∴BD=BC,
∴∠BDC=∠BCD=70°,
∴∠DBC=40°,
∴∠ADB=∠CBD=40°.
24.(1)证明:∵AB=AC,
∴∠B=∠C,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS);
(2)解:∵∠ADE=2∠B,
∴∠B=∠BAD,
∴BD=AD=2,
∵△ABD≌△ACE,
∴AE=AD=2.
25.解:(1)∵OC⊥AB,
∴∠AOC=90°,
∵OD在OA和OC之间,∠COD=25°,∠EOD=60°,
∴∠COE=60°﹣25°=35°,
∴∠AOE=90°+35°=125°,
故答案为:125;
(2)在△ODE旋转过程中,∠AOD与∠COE的差不发生变化,
有两种情况:①如图1,
∵∠AOD+∠COD=90°,∠COD+∠COE=60°,
∴∠AOD﹣∠COE=90°﹣60°=30°,
②如图2,
∵∠AOD=∠AOC+∠COD=90°+∠COD,∠COE=∠DOE+∠DOC=60°+∠DOC,
∴∠AOD﹣∠COE=(90°+∠COD)﹣(60°+∠COD)=30°,
即△ODE在旋转过程中,∠AOD与∠COE的差不发生变化,为30°;
(3)如图1、∵∠AOE=7∠COD,∠AOC=90°,∠DOE=60°,
∴90°+60°﹣∠COD=7∠COD,
解得:∠COD=18.75°,
∴∠AOE=7×18.75°=131.25°;
如图2、∵∠AOE=7∠COD,∠AOC=90°,∠DOE=60°,
∴90°+60°+∠COD=7∠COD,
∴∠COD=25°,
∴∠AOE=7×25°=175°;
即∠AOE=131.25°或175°.
26.证明:(1)∵CE⊥AB,
∴∠AEF=∠CEB=90°.
∴∠AFE+∠EAF=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠CFD+∠ECB=90°,
又∵∠AFE=∠CFD,
∴∠EAF=∠ECB.
在△AEF和△CEB中,
,
∴△AEF≌△CEB(ASA);
(2)∵△AEF≌△CEB,
∴AF=BC,
∵AB=AC,AD⊥BC
∴CD=BD,BC=2CD.
∴AF=2CD.
27.解:(1)证明∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)∵△ABD≌△ACE,
∴∠B=∠C=40°,
∵∠E=80°,
∴∠CAE=180°﹣∠C﹣∠E=180°﹣40°﹣80°=60°,
∵AD=AE,
∴∠ADE=∠E,
∴∠DAE=180°﹣2∠E=180°﹣160°=20°,
∴∠CAD=∠CAE﹣∠DAE=60°﹣20°=40°
1.如果三角形的两条边长分别是8厘米、6厘米,那么第三边的长不可能是( )
A.9厘米 B.4厘米 C.3厘米 D.2厘米
2.如果一个三角形的两个外角之和为270°,那么这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.无法确定
3.画△ABC的边BC上的高,正确的是( )
A.B.C.D.
4.如图,△ABC中,AB=15,BC=9,BD是AC边上的中线,若△ABD的周长为30,则△BCD的周长是( )
A.20 B.24 C.26 D.28
5.如图,△ABC的高CD、BE相交于点O,如果∠A=60°,那么∠BOC的大小为( )
A.60° B.100° C.120° D.130°
6.如图,将△ABC沿着DE翻折,使B点与B′点重合,若∠1+∠2=80°,则∠B的度数为( )
A.20° B.30° C.40° D.50°
7.一块三角形玻璃,被摔成如图所示的四块,小敏想去店里买一块形状、大小与原来一样的玻璃,借助“全等三角形”的相关知识,小敏只带了一块去,则这块玻璃的编号是( )
A.① B.② C.③ D.④
8.如图所示,已知∠1=∠2,则不一定能使△ABD≌△ACD的条件是( )
A.BD=CD B.∠B=∠C C.AB=AC D.AD平分∠BAC
9.已知a、b、c是△ABC的三条边长,化简|a+b﹣c|﹣|c﹣a﹣b|的结果为( )
A.2a+2b﹣2c B.2a+2b C.2c D.0
10.如图,在长方形ABCD中,AB=6cm,BC=8cm,点E是AB上的一点,且AE=2BE.点P从点C出发,以2cm/s的速度沿点C﹣D﹣A﹣E匀速运动,最终到达点E.设点P运动时间为ts,若三角形PCE的面积为18cm2,则t的值为( )
A.或 B.或或
C.或6 D.或6或
11.如图,E为△ABC的BC边上一点,点D在BA的延长线上,DE交AC于点F,∠B=46°,∠C=30°,∠EFC=70°,则∠D= .
12.如图,△ABC的面积是21,点D、E、F分别在边BC、AB、AC上,且AE=2,EB=4.若△ABD与四边形DFEB面积相等,则△ADC的面积= .
13.如图,在△ABC中,已知点D、点E分别为BC、AD的中点,且△BDE的面积为3,则△ABC的面积是 .
14.如图,点A,F,C,D在同一条直线上,BC∥EF,AC=FD,请你添加一个条件 ,使得△ABC≌△DEF.
15.如图,∠ABC与∠ACB的平分线交于I点,若∠ABC+∠ACB=100°,则∠BIC= ;若∠A=50°,则∠BIC= .
16.将一副三角板如图所示摆放,若∠BAE=125°,则∠CAD的度数是 .
17.如图,BP是△ABC中∠ABC的平分线,CP是∠ACB的外角的平分线,如果∠ABP=15°,∠ACP=50°,则∠P= °.
18.如图所示,在△ABC中,AD平分∠BAC,BE是高线,∠BAC=50°,∠EBC=20°,则∠ADC的度数为 .
19.如图,已知CD⊥AB,BE⊥AC垂足分别为D、E,BE、CD交于点O,且∠BAO=∠CAO,则图中的全等三角形共有 对.
20.如图,BE是∠ABD的平分线,CF是∠ACD的平分线,BE与CF交于G,如果∠BDC=140°,∠BGC=110°,则∠A= .
21.已知:如图,在△ABC和△DEF中,点B、E、C、F四点在一条直线上,且BE=CF,AB=DE,∠B=∠DEF.
求证:△ABC≌△DEF.
22.如图,在△ABC中,CD是AB边上的高,AE平分∠BAC,AE、CD相交于点F,若∠BAC=∠DCB.求证:∠CFE=∠CEF.
23.如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD=BE.
(1)求证:△ABD≌△ECB.
(2)若∠BDC=70°.求∠ADB的度数.
24.如图,在△ABC中,AB=AC,点D,E在BC上(BD<BE),BD=CE.
(1)求证:△ABD≌△ACE.
(2)若∠ADE=2∠B,BD=2,求AE的长.
25.如图,点O在直线AB上,OC⊥AB.在△ODE中,∠ODE=90°,∠EOD=60°.先将△ODE一边OE与OC重合,然后绕点O顺时针方向旋转,当OE与OB重合时停止旋转.
(1)当OD在OA与OC之间,且∠COD=25°时,则∠AOE= °.
(2)试探索:在△ODE旋转过程中,∠AOD与∠COE大小的差是否发生变化?若不变,请求出这个差值;若变化,请说明理由;
(3)在△ODE的旋转过程中,若∠AOE=7∠COD,试求∠AOE的大小.
26.如图,△ABC中,AB=AC,AD是BC边上的高,CE是AB边上的高,AE=CE.
求证:(1)△AEF≌△CEB;
(2)AF=2CD.
27.如图,点D是线段CE上一点,且AB=AC,AD=AE,∠BAC=∠DAE.
(1)求证:BD=CE;
(2)若∠B=40°,∠E=80°,求∠CAD的度数.
参考答案
1.解:设第三边为a,
根据三角形的三边关系可得:8﹣6<a<8+6,
解得:2<a<14.
故第三边不可能是2,
故选:D.
2.解:如图:
∵∠EAC+∠FCA=270°,
∴∠BAC+∠ACB=180°﹣∠EAC+180°﹣∠FCA=360°﹣(∠EAC+∠FCA)=90°,
∴∠B=180°﹣(∠BAC+∠ACB)=90°,
即△ABC是直角三角形.
故选:B.
3.解:A.此图形中AD是BC边上的高,符合题意;
B.此图形中CD不是BC边上的高,不符合题意;
C.此图形中CD是AB边上的高,不符合题意;
D.此图形中AD是AB边上的高,不符合题意;
故选:A.
4.解:∵BD是AC边上的中线,
∴AD=CD.
∵△ABD的周长为30,
∴AB+BD+AD=30.
∴BD+AD=30﹣AB=30﹣15=15.
∴△BCD的周长为BC+CD+BD=BC+AD+BD=9+15=24.
故选:B.
5.解:如图,
∵CD、BE均为△ABC的高,
∴∠BEC=∠ADC=90°,
∵∠A=60°,
∴∠OCE=180°﹣∠ADC﹣∠A=180°﹣90°﹣60°=30°,
则∠BOC=∠BEC+∠OCE=90°+30°=120°.
故选:C.
6.解:由翻折可知:∠BED=∠B'ED,∠BDE=∠B'DE,
∵∠1+∠BED+∠B'ED=180°,∠2+∠BDE+∠B'DE=180°,
∴∠1+2∠BED+∠2+2∠BDE=360°,
∵∠1+∠2=80°,
∴2∠BED+2∠BDE=280°,
∴∠BED+∠BDE=140°,
∵∠BED+∠BDE+∠B=180°,
∴∠B=180°﹣140°=40°.
故选:C.
7.解:因为第③块中有完整的两个角以及他们的夹边,利用ASA易证三角形全等,故应带第3块.
故选:C.
8.解:A.BD=CD,∠1=∠2,AD=AD,符合全等三角形的判定定理SAS,能推出△ABD≌△ACD,故本选项不符合题意;
B.∠B=∠C,∠1=∠2,AD=AD,符合全等三角形的判定定理AAS,能推出△ABD≌△ACD,故本选项不符合题意;
C.AB=AC,AD=AD,∠1=∠2,不符合全等三角形的判定定理,不能推出△ABD≌△ACD,故本选项符合题意;
D.∵AD平分∠BAC,
∴∠BAD=∠CAD,
∵AD=AD,∠1=∠2,
∴△ABD≌△ACD(ASA),故本选项不符合题意;
故选:C.
9.解:根据三角形的三边关系,两边之和大于第三边,
得a+b﹣c>0,c﹣a﹣b<0,
故|a+b﹣c|﹣|c﹣a﹣b|=a+b﹣c+c﹣a﹣b=0.
故选:D.
10.解:如图1,当点P在CD上,即0<t≤3时,
∵四边形ABCD是矩形,
∴AB=CD=6cm,AD=BC=8cm.
∵CP=2t(cm),
∴S△PCE=×2t×8=18,
∴t=;
如图2,当点P在BC上,即3<t≤7时,
∵AE=2BE,
∴AE=AB=4.
∵DP=2t﹣6,AP=8﹣(2t﹣6)=14﹣2t.
∴S△PCE=×(4+6)×8﹣(2t﹣6)×6﹣(14﹣2t)×4=18,
解得:t=6;
当点P在AE上,即7<t≤9时,
PE=18﹣2t.
∴S△APE=(18﹣2t)×8=18,
解得:t=<7(舍去).
综上所述,当t=或6时△APE的面积会等于18.
故选:C.
11.解:∵∠B=46°,∠C=30°,
∴∠DAC=∠B+∠C=76°,
∵∠EFC=70°,
∴∠AFD=70°,
∴∠D=180°﹣∠DAC﹣∠AFD=34°,
故答案为:34°.
12.解:如图,连接CE,AD交EF于点G
∵S△ABD=S四边形DFEB,
∴S△AEG=S△DFG,
∴S△AEG+S△AFG=S△DFG+S△AFG,
∴S△AEF=S△ADF,
设△ACE的边AC上的高为h1,
∵S△AEF=?AF?h1,S△AEC=?AC?h1,
设△ACD的边AC上的高为h2,
∵S△ADF=?AF?h2,S△ADC=?AC?h2,
∵S△AEF=S△ADF,
∴h1=h2,
∴S△AEC=S△ADC,
∵AE=2,EB=4,
∴S△AEC=S△BEC=S△ABC,
∵S△ABC=21,
∴S△AEC=7,
∴S△ADC=7.
故答案为:7.
13.解:∵点E为AD的中点,△BDE的面积为3,
∴△ABD的面积为3×2=6,
∵点D为BC的中点,
∴△ABC的面积为6×2=12.
故答案为:12.
14.解:∵BC∥EF,
∴∠BCA=∠EFD,
若添加BC=EF,且AC=FD,由“SAS”可证△ABC≌△DEF;
若添加∠B=∠E,且AC=FD,由“AAS”可证△ABC≌△DEF;
若添加∠A=∠D,且AC=FD,由“ASA”可证△ABC≌△DEF;
故答案为:BC=EF或∠B=∠E或∠A=∠D(答案不唯一).
15.解:∵BI平分∠ABC,CI平分∠ACB,
∴∠IBC=∠ABC,∠ICB=∠ACB,
∴∠IBC+∠ICB=(∠ABC+∠ACB)=50°,
∴∠BIC=180°﹣(∠IBC+∠ICB)=130°;
当∠A=50°时,∠ABC+∠ACB=180°﹣∠A=130°,
∴∠IBC+∠ICB=(∠ABC+∠ACB)=65°,
∴∠BIC=180°﹣(∠IBC+∠ICB)=115°.
故答案为:130°;115°.
16.解:∵∠BAE=125°,
∴∠DAE=∠BAE﹣∠BAD=125°﹣90°=35°,
∴∠CAD=∠CAE﹣∠DAE=90°﹣35°=55°,
故答案为:55°.
17.解:∵BP是△ABC中∠ABC的平分线,∠ABP=15°,
∴∠CBP=∠ABP=15°,
∵CP是∠ACB的外角的平分线,∠ACP=50°,
∴∠PCM=∠ACP=50°,
∴∠P=∠PCM﹣∠CBP=50°﹣15°=35°,
故答案为:35.
18.解:∵AD平分∠BAC,BE是高,∠BAC=50°,
∴∠BAD=∠BAC=25°,∠ABE=40°.
∵∠EBC=20°,
∴∠ADC=∠ABD+∠BAD=∠ABE+∠EBC+∠BAD=40°+20°+25°=85°.
故答案为:85°.
19.解:∵CD⊥AB,BE⊥AC,
∴∠ADO=∠AEO=90°,
∵AO=AO,∠DAO=∠EAO,
∴△ADO≌△AEO(AAS);
∴OD=OE,AD=AE,
∵∠DOB=∠EOC,∠ODB=∠OEC=90°,
∴△BOD≌△COE(ASA);
∴BD=CE,OB=OC,∠B=∠C;
∵AE=AD,∠DAC=∠CAB,∠ADC=∠AEB=90°;
∴△ADC≌△AEB(ASA);
∵AD=AE,BD=CE;
∴AB=AC;
∵OB=OC,AO=AO;
∴△ABO≌△ACO(SSS).
所以共有四对全等三角形.
故答案为:四.
20.解:连接BC,
∵∠BDC=140°,
∴∠DBC+∠DCB=180°﹣140°=40°,
∵∠BGC=110°,
∴∠GBC+∠GCB=180°﹣110°=70°,
∴∠GBD+∠GCD=70°﹣40°=30°,
∵BE是∠ABD的平分线,CF是∠ACD的平分线,
∴∠ABG+∠ACG=∠GBD+∠GCD=30°,
在△ABC中,∠A=180°﹣40°﹣30°﹣30°=80°.
故答案为:80°.
21.证明:∵BE=CF,
∴BE+EC=CF+EC,
即BC=EF,
在△ABC与△DEF中,
,
∴△ABC≌△DEF(SAS).
22.证明:在△ABC中,CD是高,∠BAC=∠DCB,
∴∠CDA=90°,∠BAC+∠ACD=90°,
∴∠DCB+∠ACD=90°,
∴∠ACB=90°;
∵AE是角平分线,
∴∠CAE=∠BAE,
∵∠FDA=90°,∠ACE=90°,
∴∠DAF+∠AFD=90°,∠CAE+∠CEA=90°,
∴∠AFD=∠CEA,
∵∠AFD=∠CFE,
∴∠CFE=∠CEA,
即∠CFE=∠CEF.
23.证明:(1)∵AD∥BC,
∴∠ADB=∠CBE,
在△ABD和△ECB中,
,
∴△ABD≌△ECB(ASA);
(2)∵△ABD≌△ECB,
∴BD=BC,
∴∠BDC=∠BCD=70°,
∴∠DBC=40°,
∴∠ADB=∠CBD=40°.
24.(1)证明:∵AB=AC,
∴∠B=∠C,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS);
(2)解:∵∠ADE=2∠B,
∴∠B=∠BAD,
∴BD=AD=2,
∵△ABD≌△ACE,
∴AE=AD=2.
25.解:(1)∵OC⊥AB,
∴∠AOC=90°,
∵OD在OA和OC之间,∠COD=25°,∠EOD=60°,
∴∠COE=60°﹣25°=35°,
∴∠AOE=90°+35°=125°,
故答案为:125;
(2)在△ODE旋转过程中,∠AOD与∠COE的差不发生变化,
有两种情况:①如图1,
∵∠AOD+∠COD=90°,∠COD+∠COE=60°,
∴∠AOD﹣∠COE=90°﹣60°=30°,
②如图2,
∵∠AOD=∠AOC+∠COD=90°+∠COD,∠COE=∠DOE+∠DOC=60°+∠DOC,
∴∠AOD﹣∠COE=(90°+∠COD)﹣(60°+∠COD)=30°,
即△ODE在旋转过程中,∠AOD与∠COE的差不发生变化,为30°;
(3)如图1、∵∠AOE=7∠COD,∠AOC=90°,∠DOE=60°,
∴90°+60°﹣∠COD=7∠COD,
解得:∠COD=18.75°,
∴∠AOE=7×18.75°=131.25°;
如图2、∵∠AOE=7∠COD,∠AOC=90°,∠DOE=60°,
∴90°+60°+∠COD=7∠COD,
∴∠COD=25°,
∴∠AOE=7×25°=175°;
即∠AOE=131.25°或175°.
26.证明:(1)∵CE⊥AB,
∴∠AEF=∠CEB=90°.
∴∠AFE+∠EAF=90°,
∵AD⊥BC,
∴∠ADC=90°,
∴∠CFD+∠ECB=90°,
又∵∠AFE=∠CFD,
∴∠EAF=∠ECB.
在△AEF和△CEB中,
,
∴△AEF≌△CEB(ASA);
(2)∵△AEF≌△CEB,
∴AF=BC,
∵AB=AC,AD⊥BC
∴CD=BD,BC=2CD.
∴AF=2CD.
27.解:(1)证明∵∠BAC=∠DAE,
∴∠BAC+∠CAD=∠DAE+∠CAD,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
,
∴△ABD≌△ACE(SAS),
∴BD=CE;
(2)∵△ABD≌△ACE,
∴∠B=∠C=40°,
∵∠E=80°,
∴∠CAE=180°﹣∠C﹣∠E=180°﹣40°﹣80°=60°,
∵AD=AE,
∴∠ADE=∠E,
∴∠DAE=180°﹣2∠E=180°﹣160°=20°,
∴∠CAD=∠CAE﹣∠DAE=60°﹣20°=40°
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
