2020—2021学年北师大版七年级数学下册第5章生活中的轴对称高频热点专题提升训练(word解析版)
文档属性
| 名称 | 2020—2021学年北师大版七年级数学下册第5章生活中的轴对称高频热点专题提升训练(word解析版) |  | |
| 格式 | doc | ||
| 文件大小 | 224.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 11:08:38 | ||
图片预览


文档简介
2021北师大版七年级数学下册《第5章生活中的轴对称》高频热点专题提升训练(附答案)
1.如图,已知∠B=20°,∠C=30°,若MP和QN分别垂直平分AB和AC,则∠PAQ等于( )
A.50° B.75° C.80° D.105°
2.等腰三角形的两边长分别为2cm和5cm,则该等腰三角形的周长是( )
A.7cm B.9cm C.12cm D.9cm或12cm
3.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若BC=5,AC=4,则△ACE的周长为( )
A.9 B.10 C.13 D.14
4.如图,△ABC中,∠CAB和∠CBA的角平分线交于点P,连接PA、PB、PC,若△PAB、△PBC、△PAC的面积分别为S1、S2、S3,则( )
A.S1<S2+S3 B.S1=S2+S3
C.S1>S2+S3 D.无法确定S1与(S2+S3)的大小
5.如图,△ABC中,AB=BC,点D在AC上,BD⊥BC.设∠BDC=α,∠ABD=β,则( )
A.3α+β=180° B.2α+β=180° C.3α﹣β=90° D.2α﹣β=90°
6.等腰三角形一腰上的高与另一腰的夹角等于30°,则这个等腰三角形的顶角等于( )
A.30° B.60° C.30°或150° D.60°或120°
7.已知等腰三角形的底边长为6,一条腰上的中线把三角形的周长分为两部分,其中一部分比另外一部分长2,则三角形的腰长是 .
8.如图,等腰△ABC的底边BC长为4,面积是16,腰AB的垂直平分线EF分别交AB、AC于点F、E,若点D为BC边上的中点,M为线段EF上一动点,则△BDM的周长的最小值是 .
9.已知一个等腰三角形,其中一条腰上的高与另一条腰的夹角为25°,则该等腰三角形的顶角为 .
10.如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=37°,则∠BAC= .
11.如图,AE是∠CAM的角平分线,点B在射线AM上,DE是线段BC的中垂线交AE于E,过点E作AM的垂线交AM于点F.若∠ACB=28°,∠EBD=25°,则∠AED= °.
12.如图,在△ABC中,点D是BC上的点,∠BAD=∠ABC=35°,将△ABD沿着AD翻折得到△AED,则∠CDE= °.
13.已知C,D两点在线段AB的垂直平分线上,且∠ACB=50°,∠ADB=86°,则∠CAD的度数是 .
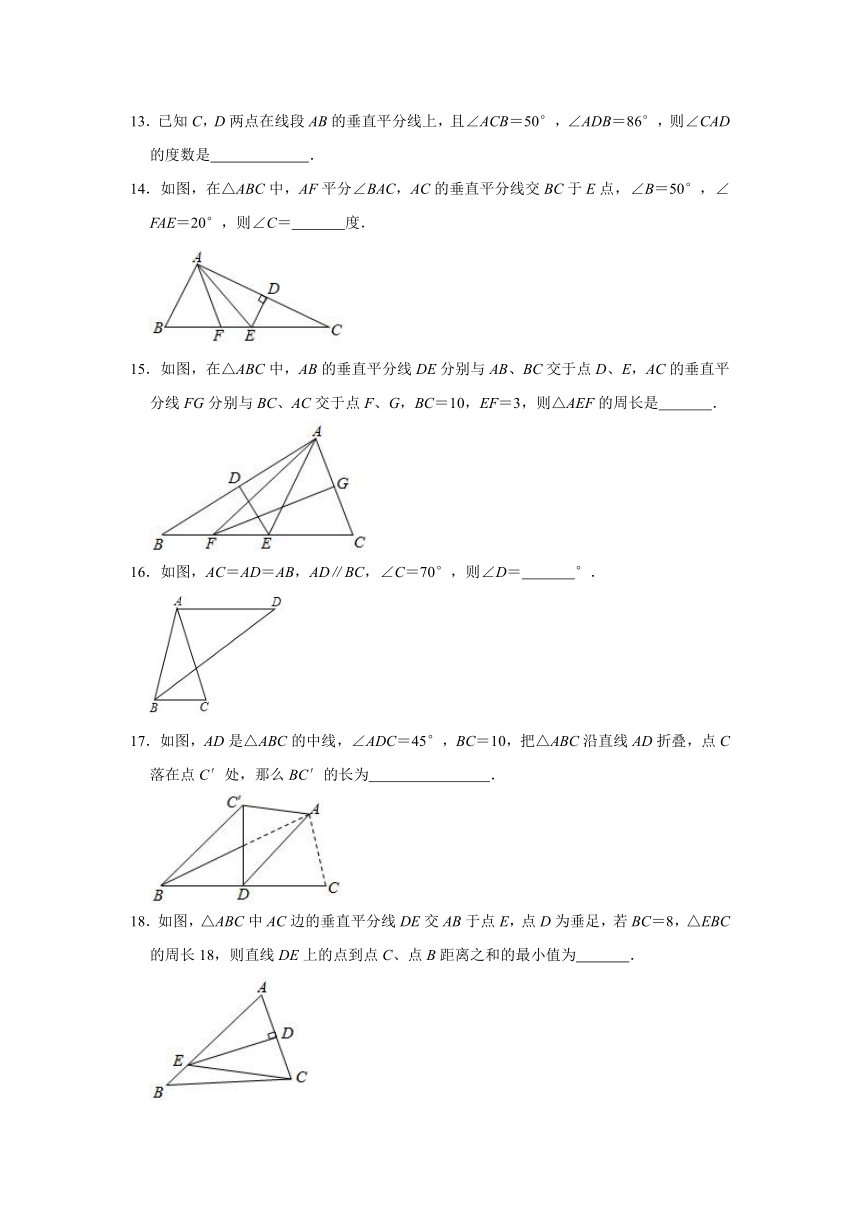
14.如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于E点,∠B=50°,∠FAE=20°,则∠C= 度.
15.如图,在△ABC中,AB的垂直平分线DE分别与AB、BC交于点D、E,AC的垂直平分线FG分别与BC、AC交于点F、G,BC=10,EF=3,则△AEF的周长是 .
16.如图,AC=AD=AB,AD∥BC,∠C=70°,则∠D= °.
17.如图,AD是△ABC的中线,∠ADC=45°,BC=10,把△ABC沿直线AD折叠,点C落在点C′处,那么BC′的长为 .
18.如图,△ABC中AC边的垂直平分线DE交AB于点E,点D为垂足,若BC=8,△EBC的周长18,则直线DE上的点到点C、点B距离之和的最小值为 .
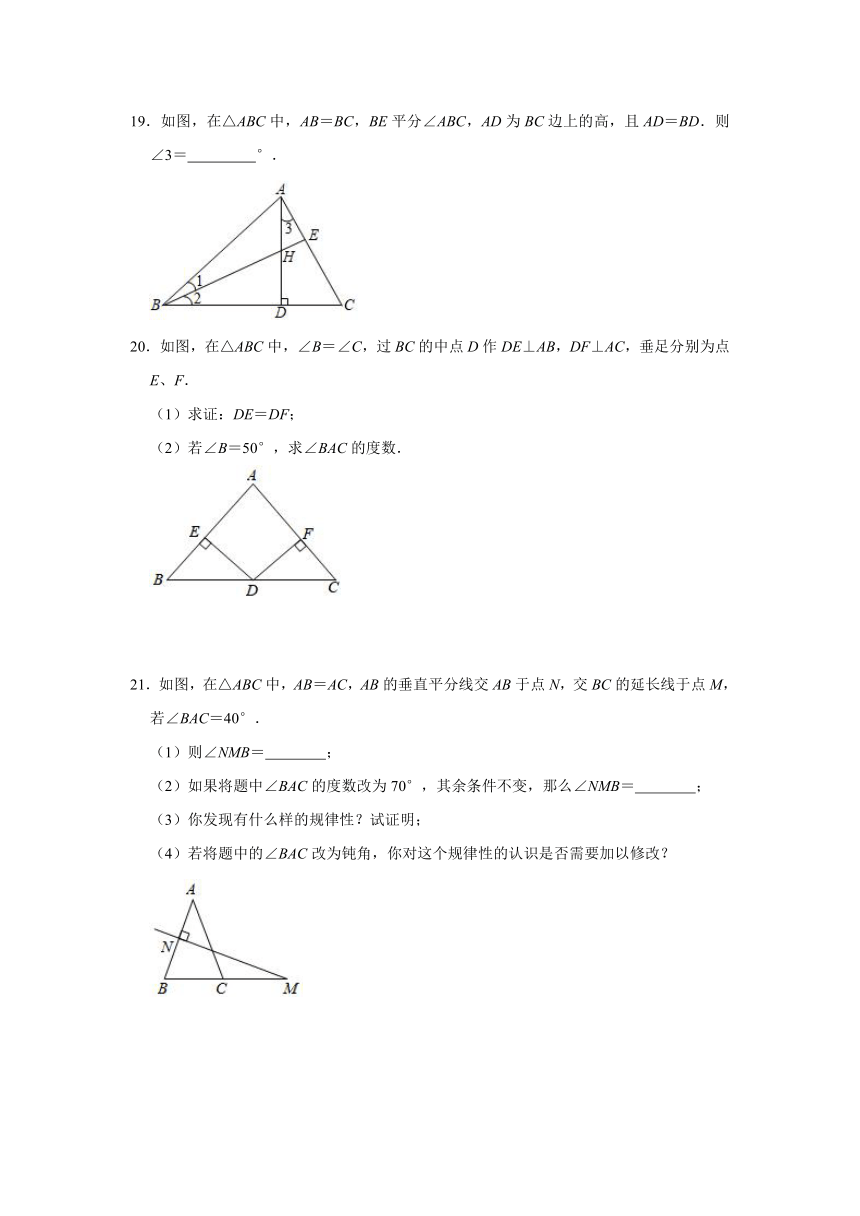
19.如图,在△ABC中,AB=BC,BE平分∠ABC,AD为BC边上的高,且AD=BD.则∠3= °.
20.如图,在△ABC中,∠B=∠C,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E、F.
(1)求证:DE=DF;
(2)若∠B=50°,求∠BAC的度数.
21.如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M,若∠BAC=40°.
(1)则∠NMB= ;
(2)如果将题中∠BAC的度数改为70°,其余条件不变,那么∠NMB= ;
(3)你发现有什么样的规律性?试证明;
(4)若将题中的∠BAC改为钝角,你对这个规律性的认识是否需要加以修改?
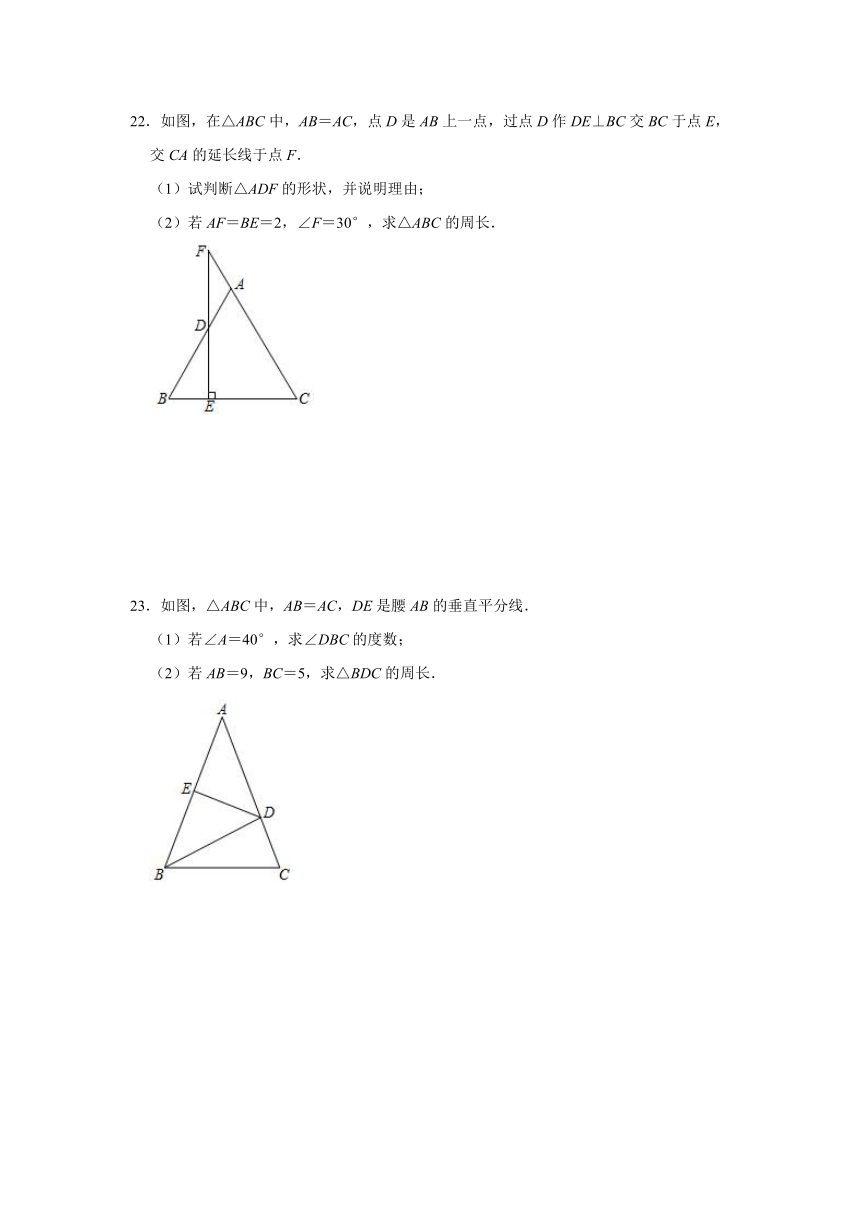
22.如图,在△ABC中,AB=AC,点D是AB上一点,过点D作DE⊥BC交BC于点E,交CA的延长线于点F.
(1)试判断△ADF的形状,并说明理由;
(2)若AF=BE=2,∠F=30°,求△ABC的周长.
23.如图,△ABC中,AB=AC,DE是腰AB的垂直平分线.
(1)若∠A=40°,求∠DBC的度数;
(2)若AB=9,BC=5,求△BDC的周长.
24.已知,在△ABC中,∠ABC=∠ACB,点D为射线CB上一点,过点D作DE⊥AC于点E.
(1)如图1,当点D在线段BC上时,请直接写出∠BAC与∠EDC的数量关系: .
(2)如图2,当点D在CB的延长线上时,画出图形,探究∠BAC与∠EDC的数量关系,并说明理由.
(3)在(2)的条件下,点F为线段BC上一点,过点F作FG⊥AC于点G,连接AF,且∠AFG=∠CFG,∠BAF=∠BFA,延长ED、AB交于点K,求∠EKA的度数.
25.如图,在△ABC中,∠ABC=70°,AB=AC=8,D为BC中点,点N在线段AD上,NM∥AC交AB于点M,BN=3.
(1)求∠CAD度数;
(2)求△BMN的周长.
26.如图,在等边△ABC中,AB=12cm,现有M,N两点分别从点A,B同时出发,沿△ABC的边按顺时针方向运动,已知点M的速度为1cm/s,点N的速度为2cm/s,当点N第一次到达B点时,M,N同时停止运动,设运动时间为t(s).
(1)当t为何值时,M,N两点重合?两点重合在什么位置?
(2)当点M,N在BC边上运动时,是否存在使AM=AN的位置?若存在,请求出此时点M,N运动的时间;若不存在,请说明理由.
27.在△ABC中,AB的垂直平分线l1交BC于点D,AC的垂直平分线l2交BC于点E,l1与l2相交于点O,△ADE的周长为6.
(1)AD与BD的数量关系为 .
(2)求BC的长.
(3)分别连接OA,OB,OC,若△OBC的周长为16,求OA的长.
参考答案
1.解:在△ABC中,∠B=20°,∠C=30°,
∴∠BAC=180°﹣20°﹣30°=130°,
∵MP和QN分别垂直平分AB和AC,
∴PA=PB,QA=QC,
∴∠PAB=∠B=20°,∠QAC=∠C=30°,
∴∠PAQ=130°﹣20°﹣30°=80°,
故选:C.
2.解:当腰长是2cm时,因为2+2<5,不符合三角形的三边关系,舍去;
当腰长是5cm时,因为2+5>5,符合三角形三边关系,此时周长是12cm.
故选:C.
3.解:∵DE是线段AB的垂直平分线,
∴EA=EB,
∴△ACE的周长=EA+EC+AC=EB+EC+AC=BC+AC=9,
故选:A.
4.解:过P点作PD⊥AB于D,PE⊥AC于E,PF⊥BC于F,如图,
∵∠CAB和∠CBA的角平分线交于点P,
∴PD=PE=PF,
∵S1=?AB?PD,S2=?BC?PF,S3=?AC?PE,
∴S2+S3=?(AC+BC)?PD,
∵AB<AC+BC,
∴S1<S2+S3.
故选:A.
5.解:∵AB=BC,
∴∠A=∠C,
∵α﹣∠A=β,α+∠C=90°,
∴2α=90°+β,
∴2α﹣β=90°,
故选:D.
6.解:当高在三角形内部时,如图1,
∵∠ABD=30°,BD⊥AC,
∴∠A=60°;
∴顶角是60°;
当高在三角形外部时,如图2,
∵∠ABD=30°,BD⊥AC于D,
∴∠BAD=60°,
∴∠BAC=180°﹣60°=120°
∴顶角是120°.
故选:D.
7.解:等腰三角形一条腰上的中线把三角形的周长分为两部分,这两部分的差即是腰与底的差的绝对值,
∵其中一部分比另外一部分长2,
∴腰比底大2或底比腰大2,
∴腰为8或4.
故答案为:8或4.
8.解:如图,连接AD.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=?BC?AD=×4×AD=16.
∴AD=8.
∵EF是线段AB的垂直平分线,
∴点B关于直线EF的对称点为点A,
∴AD的长为BM+MD的最小值,
∴△BDM的周长最短=(BM+MD)+BD=AD+BC=6+×8=10.
故答案为:10.
9.解:①如图,等腰三角形为锐角三角形,
∵BD⊥AC,∠ABD=25°,
∴∠A=65°,
即顶角的度数为65°.
②如图,等腰三角形为钝角三角形,
∵BD⊥AC,∠DBA=25°,
∴∠BAD=65°,
∴∠BAC=115°.
故答案为65°或115°.
10.解:∵AE∥BD,
∴∠DBC=∠E=37°,
∵BD平分∠ABC,
∴∠ABC=2∠DBC=74°,
∵AB=AC,
∴∠C=∠ABC=74°,
∴∠BAC=180°﹣∠ABC﹣∠C=32°.
故答案为:32°.
11.解:连接CE,过E作ER⊥AC于R,CD交ER于Q,AE交BC于O,
∵DE是线段BC的中垂线,
∴∠EDC=90°,CE=BE,
∴∠ECB=∠EBD,
∵∠EBD=25°,
∴∠ECB=25°,
∴∠DEB=∠CED=90°﹣25°=65°,
∵ER⊥AC,ED⊥BC,
∴∠QRC=∠QDE=90°,
∴∠ACB+∠CQR=90°,∠EQD+∠QED=90°,
∵∠CQR=∠EQD,
∴∠ACB=∠QED,
∵∠ACB=28°,
∴∠QED=28°,
∵AE平分∠CAM,ER⊥AC,EF⊥AM,
∴ER=EF,
在Rt△ERC和Rt△EFB中,
,
∴Rt△ERC≌Rt△EFB(HL),
∴∠EBF=∠ACE=∠ACB+∠ECD=28°+25°=53°,
∵∠EFB=90°,
∴∠BEF=90°﹣∠EBF=90°﹣53°=37°,
∴∠REF=∠RED+∠BED+∠BEF=28°+65°+37°=130°,
∵∠ARE=∠AFE=90°,
∴∠CAM=360°﹣90°﹣90°﹣130°=50°,
∵AE平分∠CAM,
∴∠CAE=CAM=25°,
∴∠DOE=∠CAE+∠ACB=25°+28°=53°,
∵ED⊥BC,
∴∠EDB=90°,
∴∠AED=90°﹣∠DOE=90°﹣53°=37°,
故答案为:37.
12.解:∵∠BAD=∠ABC=35°,
∴∠ADC=∠BAD+∠ABC=35°+35°=70°,∠ADB=180°﹣35°﹣35°=110°,
∵将△ABD沿着AD翻折得到△AED,
∴∠ADE=∠ADB=110°,
∴∠CDE=∠ADE﹣∠ADC=110°﹣70°=40°,
故答案为:40.
13.解:∵C、D两点在线段AB的中垂线上,
∴CA=CB,DA=DB,
∵CD⊥AB,
∴∠ACD=∠ACB=×50°=25°,∠ADC=∠ADB=×86°=43°,
当点C与点D在线段AB两侧时,∠CAD=180°﹣∠ACD﹣∠ADC=180°﹣25°﹣43°=112°,
当点C与点D′在线段AB同侧时,∠CAD′=∠AD′C﹣∠ACD′=43°﹣25°=18°,
故答案为:18°或112°.
14.解:∵DE是线段AC的垂直平分线,
∴EA=EC,
∴∠EAC=∠C,
∵AF平分∠BAC,
∴∠BAF=∠CAF=∠FAE+∠CAE=20°+∠C,
由三角形内角和定理得,∠B+∠BAC+∠C=180°,即50°+20°+∠C+20°+∠C+∠C=180°,
解得,∠C=30°,
故答案为:30.
15.解:∵DE是线段AB的垂直平分线,
∴EA=EB,
同理,FA=FC,
∴△AEF的周长=FA+EF+EA=EB+EF+FC=BC+EF+EF=16,
故答案为:16.
16.解:∵AD∥BC,
∴∠C=∠DAC=70°,
∵AB=AC,
∴∠ABC=∠C=70°,
∴∠BAC=180°﹣140°=40°,
∴∠BAD=110°,
∵AB=AD,
∴∠D=(180°﹣∠BAD)=35°,
故答案为:35.
17.解:∵AD是△ABC的中线,BC=10,
∴BD=CD=5,
∵把△ABC沿直线AD折叠,
∴CD=C'D,∠ADC=∠ADC'=45°,
∴BD=C'D=5,∠BDC'=90°,
∴BC'====5,
故答案为:.
18.解:如图,DE上取一点P,连接PA,PB,PC.
∵DE垂直平分线段AC,
∴PA=PC,EA=EC,
∴PB+PC=PB+PA≥AB,
∴当点P与E重合时,PB+PC的值最小,最小值就是线段AB的长,
∵△EBC的周长=EB+EC+BC=EB+EA+BC=AB+BC=18,BC=8,
∴AB=18﹣8=10,
∴直线DE上的点到点C、点B距离之和的最小值为10,
故答案为:10.
19.解:∵AD为BC边上的高,
∴∠ADB=90°,
∵AD=BD,
∴∠ABD=∠BAD=(180°﹣∠ADB)=45°,
∵BE平分∠ABC,
∴∠1=∠2=∠ABD=22.5°,BE⊥AC,
∴∠BEA=90°=∠ADB,
∵∠3+∠BEA+∠AHE=180°,∠2+∠ADB+∠BHD=180°,∠AHE=∠BHD,
∴∠3=∠2=22.5°.
故答案为:22.5°.
20.(1)证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
∵D是BC的中点,
∴BD=CD,
在△BED与△CFD中,
,
∴△BED≌△CFD(AAS),
∴DE=DF;
(2)解:∵∠B=50°,
∴∠C=∠B=50°,
∴∠BAC=180°﹣50°﹣50°=80°.
21.解:(1)∵AB=AC,∠BAC=40°,
∴,
∴∠CDM=∠ADN=90°﹣∠A=50°,
∴∠NMB=∠ACB﹣∠CDM=20°.
故答案为:20°.
(2)∵AB=AC,∠BAC=70°,
∴,
∴∠CDM=∠ADN=90°﹣∠A=20°,
∴∠NMB=∠ACB﹣∠CDM=35°.
故答案为:35°.
(3)上述规律为:等腰三角形一腰的垂直平分线与底边相交所成的锐角等于顶角的一半.
证明:设∠A=α,
∵AB=AC,
∴∠B=∠C,
∴∠B=(180°﹣∠A)=(180°﹣α),
∵∠BNM=90°,
∴∠NMB=90°﹣∠B=90°﹣(180°﹣α)=α;
(4)将(1)中的∠A改为钝角,(3)中猜想的结论仍然成立.
证明:设∠A=α,
∵AB=AC,
∴∠B=∠C,
∴∠B=(180°﹣∠A)=(180°﹣α),
∵∠BNM=90°,
∴∠NMB=90°﹣∠B=90°﹣(180°﹣α)=α.
22.解:(1)∵AB=AC,
∴∠B=∠C,
∵FE⊥BC,
∴∠F+∠C=90°,∠BDE+∠B=90°,
∴∠F=∠BDE,
而∠BDE=∠FDA,
∴∠F=∠FDA,
∴AF=AD,
∴△ADF是等腰三角形;
(2)∵AF=AD=2,∠F=30°,
∴∠ADF=∠F=30°,
∵DE⊥BC,
∴∠DEB=90°,
∴DB=2BE=4,
∴AB=AD+DB=6,
∵∠F=30°,
∴∠C=60°,
∵AB=AC,
∴△ABC是等边三角形,
∴△ABC的周长为18.
23.解:(1)∵△ABC中,AB=AC,∠A=40°,
∴∠ABC==70°.
∵DE是腰AB的垂直平分线,
∴AD=BD,∠DBA=∠A=40°,
∴∠DBC=70°﹣40°=30°;
(2)由(1)得:AD=BD,
∴△BDC的周长=BD+CD+BC=AD+CD+BC=AC+BC=AB+BC=9+5=14.
答:△BDC的周长是14.
24.(1)如图1中,作AH⊥BC于H.
∵AB=AC,AH⊥BC,
∴∠BAH=∠CAH,
∵DE⊥AC,
∴∠AHC=∠CED=90°,
∴∠C+∠CAH=90°,∠C+∠EDC=90°,
∴∠CAH=∠EDC,
∴∠BAC=2∠EDC.
故答案为∠BAC=2∠EDC.
(2)如图2中,结论:∠BAC=2∠EDC.
理由:∵AB=AC,AH⊥BC,
∴∠BAH=∠CAH,
∵DE⊥AC,
∴∠AHC=∠CED=90°,
∴∠C+∠CAH=90°,∠C+∠EDC=90°,
∴∠CAH=∠EDC,
∴∠BAC=2∠EDC.
(3)如图2中,设∠C=∠FAC=∠ABC=x,则∠BAF=∠BFA=2x,
∴5x=180°,
∴x=36°,
∴∠EAK=∠ABC+∠C=72°,
∵KE⊥EC,
∴∠E=90°,
∴∠EKA=90°﹣72°=18°.
25.解:(1)∵AB=AC,
∴△ABC是等腰三角形,
又∵∠ABC=70°,
∴∠BAC=180°﹣70°×2=40°,
又∵D为AB中点,
∴AD平分∠BAC,
∴∠CAD=∠BAD=∠BAC=×40°=20°,
故∠CAD度数为20°.
(2)∵NM∥AC,
∴∠ANM=∠CAD,
又∵∠CAD=∠BAD,
∴∠ANM=∠BAD,
∴AM=NM,
∴△BMN的周长=MB+BN+NM=AB+BN,
∵AB=8,BN=3,
∴△BMN的周长=8+3=11.
故△BMN的周长为11.
26.解:(1)由题意,t×1+12=2t,
解得:t=12,
∴当t=12时,M,N两点重合,
此时两点在点C处重合;
(2)结论:当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形.
理由:由(1)知12秒时M、N两点重合,恰好在C处,
如图,假设△AMN是等腰三角形,
∴AN=AM,
∴∠AMN=∠ANM,
∴∠AMC=∠ANB,
∵△ACB是等边三角形,
∴∠C=∠B,
在△ACM和△ABN中,
,
∴△ACM≌△ABN(AAS),
∴CM=BN,
设当点M、N在BC边上运动时,M、N运动的时间y秒时,△AMN是等腰三角形,
∴CM=y﹣12,NB=36﹣2y,
∵CM=NB,
∴y﹣12=36﹣2y,
解得:y=16.故假设成立.
∴当点M、N在BC边上运动时,能得到以MN为底边的等腰三角形AMN,此时M、N运动的时间为16秒.
27.解:(1)∵l1是线段AB的垂直平分线,
∴AD=BD,
故答案为:AD=BD;
(2)∵l2是线段AC的垂直平分线,
∴EA=EC,
∵△ADE的周长为6,
∴AD+DE+AE=6,
∴BD+DE+EC=6,即BC=6;
(3)∵l1是线段AB的垂直平分线,
∴OA=OB,
∵l2是线段AC的垂直平分线,
OA=OC,
∴OB=OC,
∵△OBC的周长为16,BC=6,
∴OB+OC=10,
∴OA=OB=OC=5.
1.如图,已知∠B=20°,∠C=30°,若MP和QN分别垂直平分AB和AC,则∠PAQ等于( )
A.50° B.75° C.80° D.105°
2.等腰三角形的两边长分别为2cm和5cm,则该等腰三角形的周长是( )
A.7cm B.9cm C.12cm D.9cm或12cm
3.如图,在△ABC中,AB的垂直平分线交AB于点D,交BC于点E,连接AE.若BC=5,AC=4,则△ACE的周长为( )
A.9 B.10 C.13 D.14
4.如图,△ABC中,∠CAB和∠CBA的角平分线交于点P,连接PA、PB、PC,若△PAB、△PBC、△PAC的面积分别为S1、S2、S3,则( )
A.S1<S2+S3 B.S1=S2+S3
C.S1>S2+S3 D.无法确定S1与(S2+S3)的大小
5.如图,△ABC中,AB=BC,点D在AC上,BD⊥BC.设∠BDC=α,∠ABD=β,则( )
A.3α+β=180° B.2α+β=180° C.3α﹣β=90° D.2α﹣β=90°
6.等腰三角形一腰上的高与另一腰的夹角等于30°,则这个等腰三角形的顶角等于( )
A.30° B.60° C.30°或150° D.60°或120°
7.已知等腰三角形的底边长为6,一条腰上的中线把三角形的周长分为两部分,其中一部分比另外一部分长2,则三角形的腰长是 .
8.如图,等腰△ABC的底边BC长为4,面积是16,腰AB的垂直平分线EF分别交AB、AC于点F、E,若点D为BC边上的中点,M为线段EF上一动点,则△BDM的周长的最小值是 .
9.已知一个等腰三角形,其中一条腰上的高与另一条腰的夹角为25°,则该等腰三角形的顶角为 .
10.如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E,若∠E=37°,则∠BAC= .
11.如图,AE是∠CAM的角平分线,点B在射线AM上,DE是线段BC的中垂线交AE于E,过点E作AM的垂线交AM于点F.若∠ACB=28°,∠EBD=25°,则∠AED= °.
12.如图,在△ABC中,点D是BC上的点,∠BAD=∠ABC=35°,将△ABD沿着AD翻折得到△AED,则∠CDE= °.
13.已知C,D两点在线段AB的垂直平分线上,且∠ACB=50°,∠ADB=86°,则∠CAD的度数是 .
14.如图,在△ABC中,AF平分∠BAC,AC的垂直平分线交BC于E点,∠B=50°,∠FAE=20°,则∠C= 度.
15.如图,在△ABC中,AB的垂直平分线DE分别与AB、BC交于点D、E,AC的垂直平分线FG分别与BC、AC交于点F、G,BC=10,EF=3,则△AEF的周长是 .
16.如图,AC=AD=AB,AD∥BC,∠C=70°,则∠D= °.
17.如图,AD是△ABC的中线,∠ADC=45°,BC=10,把△ABC沿直线AD折叠,点C落在点C′处,那么BC′的长为 .
18.如图,△ABC中AC边的垂直平分线DE交AB于点E,点D为垂足,若BC=8,△EBC的周长18,则直线DE上的点到点C、点B距离之和的最小值为 .
19.如图,在△ABC中,AB=BC,BE平分∠ABC,AD为BC边上的高,且AD=BD.则∠3= °.
20.如图,在△ABC中,∠B=∠C,过BC的中点D作DE⊥AB,DF⊥AC,垂足分别为点E、F.
(1)求证:DE=DF;
(2)若∠B=50°,求∠BAC的度数.
21.如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点N,交BC的延长线于点M,若∠BAC=40°.
(1)则∠NMB= ;
(2)如果将题中∠BAC的度数改为70°,其余条件不变,那么∠NMB= ;
(3)你发现有什么样的规律性?试证明;
(4)若将题中的∠BAC改为钝角,你对这个规律性的认识是否需要加以修改?
22.如图,在△ABC中,AB=AC,点D是AB上一点,过点D作DE⊥BC交BC于点E,交CA的延长线于点F.
(1)试判断△ADF的形状,并说明理由;
(2)若AF=BE=2,∠F=30°,求△ABC的周长.
23.如图,△ABC中,AB=AC,DE是腰AB的垂直平分线.
(1)若∠A=40°,求∠DBC的度数;
(2)若AB=9,BC=5,求△BDC的周长.
24.已知,在△ABC中,∠ABC=∠ACB,点D为射线CB上一点,过点D作DE⊥AC于点E.
(1)如图1,当点D在线段BC上时,请直接写出∠BAC与∠EDC的数量关系: .
(2)如图2,当点D在CB的延长线上时,画出图形,探究∠BAC与∠EDC的数量关系,并说明理由.
(3)在(2)的条件下,点F为线段BC上一点,过点F作FG⊥AC于点G,连接AF,且∠AFG=∠CFG,∠BAF=∠BFA,延长ED、AB交于点K,求∠EKA的度数.
25.如图,在△ABC中,∠ABC=70°,AB=AC=8,D为BC中点,点N在线段AD上,NM∥AC交AB于点M,BN=3.
(1)求∠CAD度数;
(2)求△BMN的周长.
26.如图,在等边△ABC中,AB=12cm,现有M,N两点分别从点A,B同时出发,沿△ABC的边按顺时针方向运动,已知点M的速度为1cm/s,点N的速度为2cm/s,当点N第一次到达B点时,M,N同时停止运动,设运动时间为t(s).
(1)当t为何值时,M,N两点重合?两点重合在什么位置?
(2)当点M,N在BC边上运动时,是否存在使AM=AN的位置?若存在,请求出此时点M,N运动的时间;若不存在,请说明理由.
27.在△ABC中,AB的垂直平分线l1交BC于点D,AC的垂直平分线l2交BC于点E,l1与l2相交于点O,△ADE的周长为6.
(1)AD与BD的数量关系为 .
(2)求BC的长.
(3)分别连接OA,OB,OC,若△OBC的周长为16,求OA的长.
参考答案
1.解:在△ABC中,∠B=20°,∠C=30°,
∴∠BAC=180°﹣20°﹣30°=130°,
∵MP和QN分别垂直平分AB和AC,
∴PA=PB,QA=QC,
∴∠PAB=∠B=20°,∠QAC=∠C=30°,
∴∠PAQ=130°﹣20°﹣30°=80°,
故选:C.
2.解:当腰长是2cm时,因为2+2<5,不符合三角形的三边关系,舍去;
当腰长是5cm时,因为2+5>5,符合三角形三边关系,此时周长是12cm.
故选:C.
3.解:∵DE是线段AB的垂直平分线,
∴EA=EB,
∴△ACE的周长=EA+EC+AC=EB+EC+AC=BC+AC=9,
故选:A.
4.解:过P点作PD⊥AB于D,PE⊥AC于E,PF⊥BC于F,如图,
∵∠CAB和∠CBA的角平分线交于点P,
∴PD=PE=PF,
∵S1=?AB?PD,S2=?BC?PF,S3=?AC?PE,
∴S2+S3=?(AC+BC)?PD,
∵AB<AC+BC,
∴S1<S2+S3.
故选:A.
5.解:∵AB=BC,
∴∠A=∠C,
∵α﹣∠A=β,α+∠C=90°,
∴2α=90°+β,
∴2α﹣β=90°,
故选:D.
6.解:当高在三角形内部时,如图1,
∵∠ABD=30°,BD⊥AC,
∴∠A=60°;
∴顶角是60°;
当高在三角形外部时,如图2,
∵∠ABD=30°,BD⊥AC于D,
∴∠BAD=60°,
∴∠BAC=180°﹣60°=120°
∴顶角是120°.
故选:D.
7.解:等腰三角形一条腰上的中线把三角形的周长分为两部分,这两部分的差即是腰与底的差的绝对值,
∵其中一部分比另外一部分长2,
∴腰比底大2或底比腰大2,
∴腰为8或4.
故答案为:8或4.
8.解:如图,连接AD.
∵△ABC是等腰三角形,点D是BC边的中点,
∴AD⊥BC,
∴S△ABC=?BC?AD=×4×AD=16.
∴AD=8.
∵EF是线段AB的垂直平分线,
∴点B关于直线EF的对称点为点A,
∴AD的长为BM+MD的最小值,
∴△BDM的周长最短=(BM+MD)+BD=AD+BC=6+×8=10.
故答案为:10.
9.解:①如图,等腰三角形为锐角三角形,
∵BD⊥AC,∠ABD=25°,
∴∠A=65°,
即顶角的度数为65°.
②如图,等腰三角形为钝角三角形,
∵BD⊥AC,∠DBA=25°,
∴∠BAD=65°,
∴∠BAC=115°.
故答案为65°或115°.
10.解:∵AE∥BD,
∴∠DBC=∠E=37°,
∵BD平分∠ABC,
∴∠ABC=2∠DBC=74°,
∵AB=AC,
∴∠C=∠ABC=74°,
∴∠BAC=180°﹣∠ABC﹣∠C=32°.
故答案为:32°.
11.解:连接CE,过E作ER⊥AC于R,CD交ER于Q,AE交BC于O,
∵DE是线段BC的中垂线,
∴∠EDC=90°,CE=BE,
∴∠ECB=∠EBD,
∵∠EBD=25°,
∴∠ECB=25°,
∴∠DEB=∠CED=90°﹣25°=65°,
∵ER⊥AC,ED⊥BC,
∴∠QRC=∠QDE=90°,
∴∠ACB+∠CQR=90°,∠EQD+∠QED=90°,
∵∠CQR=∠EQD,
∴∠ACB=∠QED,
∵∠ACB=28°,
∴∠QED=28°,
∵AE平分∠CAM,ER⊥AC,EF⊥AM,
∴ER=EF,
在Rt△ERC和Rt△EFB中,
,
∴Rt△ERC≌Rt△EFB(HL),
∴∠EBF=∠ACE=∠ACB+∠ECD=28°+25°=53°,
∵∠EFB=90°,
∴∠BEF=90°﹣∠EBF=90°﹣53°=37°,
∴∠REF=∠RED+∠BED+∠BEF=28°+65°+37°=130°,
∵∠ARE=∠AFE=90°,
∴∠CAM=360°﹣90°﹣90°﹣130°=50°,
∵AE平分∠CAM,
∴∠CAE=CAM=25°,
∴∠DOE=∠CAE+∠ACB=25°+28°=53°,
∵ED⊥BC,
∴∠EDB=90°,
∴∠AED=90°﹣∠DOE=90°﹣53°=37°,
故答案为:37.
12.解:∵∠BAD=∠ABC=35°,
∴∠ADC=∠BAD+∠ABC=35°+35°=70°,∠ADB=180°﹣35°﹣35°=110°,
∵将△ABD沿着AD翻折得到△AED,
∴∠ADE=∠ADB=110°,
∴∠CDE=∠ADE﹣∠ADC=110°﹣70°=40°,
故答案为:40.
13.解:∵C、D两点在线段AB的中垂线上,
∴CA=CB,DA=DB,
∵CD⊥AB,
∴∠ACD=∠ACB=×50°=25°,∠ADC=∠ADB=×86°=43°,
当点C与点D在线段AB两侧时,∠CAD=180°﹣∠ACD﹣∠ADC=180°﹣25°﹣43°=112°,
当点C与点D′在线段AB同侧时,∠CAD′=∠AD′C﹣∠ACD′=43°﹣25°=18°,
故答案为:18°或112°.
14.解:∵DE是线段AC的垂直平分线,
∴EA=EC,
∴∠EAC=∠C,
∵AF平分∠BAC,
∴∠BAF=∠CAF=∠FAE+∠CAE=20°+∠C,
由三角形内角和定理得,∠B+∠BAC+∠C=180°,即50°+20°+∠C+20°+∠C+∠C=180°,
解得,∠C=30°,
故答案为:30.
15.解:∵DE是线段AB的垂直平分线,
∴EA=EB,
同理,FA=FC,
∴△AEF的周长=FA+EF+EA=EB+EF+FC=BC+EF+EF=16,
故答案为:16.
16.解:∵AD∥BC,
∴∠C=∠DAC=70°,
∵AB=AC,
∴∠ABC=∠C=70°,
∴∠BAC=180°﹣140°=40°,
∴∠BAD=110°,
∵AB=AD,
∴∠D=(180°﹣∠BAD)=35°,
故答案为:35.
17.解:∵AD是△ABC的中线,BC=10,
∴BD=CD=5,
∵把△ABC沿直线AD折叠,
∴CD=C'D,∠ADC=∠ADC'=45°,
∴BD=C'D=5,∠BDC'=90°,
∴BC'====5,
故答案为:.
18.解:如图,DE上取一点P,连接PA,PB,PC.
∵DE垂直平分线段AC,
∴PA=PC,EA=EC,
∴PB+PC=PB+PA≥AB,
∴当点P与E重合时,PB+PC的值最小,最小值就是线段AB的长,
∵△EBC的周长=EB+EC+BC=EB+EA+BC=AB+BC=18,BC=8,
∴AB=18﹣8=10,
∴直线DE上的点到点C、点B距离之和的最小值为10,
故答案为:10.
19.解:∵AD为BC边上的高,
∴∠ADB=90°,
∵AD=BD,
∴∠ABD=∠BAD=(180°﹣∠ADB)=45°,
∵BE平分∠ABC,
∴∠1=∠2=∠ABD=22.5°,BE⊥AC,
∴∠BEA=90°=∠ADB,
∵∠3+∠BEA+∠AHE=180°,∠2+∠ADB+∠BHD=180°,∠AHE=∠BHD,
∴∠3=∠2=22.5°.
故答案为:22.5°.
20.(1)证明:∵DE⊥AB,DF⊥AC,
∴∠BED=∠CFD=90°,
∵D是BC的中点,
∴BD=CD,
在△BED与△CFD中,
,
∴△BED≌△CFD(AAS),
∴DE=DF;
(2)解:∵∠B=50°,
∴∠C=∠B=50°,
∴∠BAC=180°﹣50°﹣50°=80°.
21.解:(1)∵AB=AC,∠BAC=40°,
∴,
∴∠CDM=∠ADN=90°﹣∠A=50°,
∴∠NMB=∠ACB﹣∠CDM=20°.
故答案为:20°.
(2)∵AB=AC,∠BAC=70°,
∴,
∴∠CDM=∠ADN=90°﹣∠A=20°,
∴∠NMB=∠ACB﹣∠CDM=35°.
故答案为:35°.
(3)上述规律为:等腰三角形一腰的垂直平分线与底边相交所成的锐角等于顶角的一半.
证明:设∠A=α,
∵AB=AC,
∴∠B=∠C,
∴∠B=(180°﹣∠A)=(180°﹣α),
∵∠BNM=90°,
∴∠NMB=90°﹣∠B=90°﹣(180°﹣α)=α;
(4)将(1)中的∠A改为钝角,(3)中猜想的结论仍然成立.
证明:设∠A=α,
∵AB=AC,
∴∠B=∠C,
∴∠B=(180°﹣∠A)=(180°﹣α),
∵∠BNM=90°,
∴∠NMB=90°﹣∠B=90°﹣(180°﹣α)=α.
22.解:(1)∵AB=AC,
∴∠B=∠C,
∵FE⊥BC,
∴∠F+∠C=90°,∠BDE+∠B=90°,
∴∠F=∠BDE,
而∠BDE=∠FDA,
∴∠F=∠FDA,
∴AF=AD,
∴△ADF是等腰三角形;
(2)∵AF=AD=2,∠F=30°,
∴∠ADF=∠F=30°,
∵DE⊥BC,
∴∠DEB=90°,
∴DB=2BE=4,
∴AB=AD+DB=6,
∵∠F=30°,
∴∠C=60°,
∵AB=AC,
∴△ABC是等边三角形,
∴△ABC的周长为18.
23.解:(1)∵△ABC中,AB=AC,∠A=40°,
∴∠ABC==70°.
∵DE是腰AB的垂直平分线,
∴AD=BD,∠DBA=∠A=40°,
∴∠DBC=70°﹣40°=30°;
(2)由(1)得:AD=BD,
∴△BDC的周长=BD+CD+BC=AD+CD+BC=AC+BC=AB+BC=9+5=14.
答:△BDC的周长是14.
24.(1)如图1中,作AH⊥BC于H.
∵AB=AC,AH⊥BC,
∴∠BAH=∠CAH,
∵DE⊥AC,
∴∠AHC=∠CED=90°,
∴∠C+∠CAH=90°,∠C+∠EDC=90°,
∴∠CAH=∠EDC,
∴∠BAC=2∠EDC.
故答案为∠BAC=2∠EDC.
(2)如图2中,结论:∠BAC=2∠EDC.
理由:∵AB=AC,AH⊥BC,
∴∠BAH=∠CAH,
∵DE⊥AC,
∴∠AHC=∠CED=90°,
∴∠C+∠CAH=90°,∠C+∠EDC=90°,
∴∠CAH=∠EDC,
∴∠BAC=2∠EDC.
(3)如图2中,设∠C=∠FAC=∠ABC=x,则∠BAF=∠BFA=2x,
∴5x=180°,
∴x=36°,
∴∠EAK=∠ABC+∠C=72°,
∵KE⊥EC,
∴∠E=90°,
∴∠EKA=90°﹣72°=18°.
25.解:(1)∵AB=AC,
∴△ABC是等腰三角形,
又∵∠ABC=70°,
∴∠BAC=180°﹣70°×2=40°,
又∵D为AB中点,
∴AD平分∠BAC,
∴∠CAD=∠BAD=∠BAC=×40°=20°,
故∠CAD度数为20°.
(2)∵NM∥AC,
∴∠ANM=∠CAD,
又∵∠CAD=∠BAD,
∴∠ANM=∠BAD,
∴AM=NM,
∴△BMN的周长=MB+BN+NM=AB+BN,
∵AB=8,BN=3,
∴△BMN的周长=8+3=11.
故△BMN的周长为11.
26.解:(1)由题意,t×1+12=2t,
解得:t=12,
∴当t=12时,M,N两点重合,
此时两点在点C处重合;
(2)结论:当点M、N在BC边上运动时,可以得到以MN为底边的等腰三角形.
理由:由(1)知12秒时M、N两点重合,恰好在C处,
如图,假设△AMN是等腰三角形,
∴AN=AM,
∴∠AMN=∠ANM,
∴∠AMC=∠ANB,
∵△ACB是等边三角形,
∴∠C=∠B,
在△ACM和△ABN中,
,
∴△ACM≌△ABN(AAS),
∴CM=BN,
设当点M、N在BC边上运动时,M、N运动的时间y秒时,△AMN是等腰三角形,
∴CM=y﹣12,NB=36﹣2y,
∵CM=NB,
∴y﹣12=36﹣2y,
解得:y=16.故假设成立.
∴当点M、N在BC边上运动时,能得到以MN为底边的等腰三角形AMN,此时M、N运动的时间为16秒.
27.解:(1)∵l1是线段AB的垂直平分线,
∴AD=BD,
故答案为:AD=BD;
(2)∵l2是线段AC的垂直平分线,
∴EA=EC,
∵△ADE的周长为6,
∴AD+DE+AE=6,
∴BD+DE+EC=6,即BC=6;
(3)∵l1是线段AB的垂直平分线,
∴OA=OB,
∵l2是线段AC的垂直平分线,
OA=OC,
∴OB=OC,
∵△OBC的周长为16,BC=6,
∴OB+OC=10,
∴OA=OB=OC=5.
