2020-2021学年苏科版八年级数学下册《第11章 反比例函数》章末过关达标检测(Word版 含答案)
文档属性
| 名称 | 2020-2021学年苏科版八年级数学下册《第11章 反比例函数》章末过关达标检测(Word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 13:16:20 | ||
图片预览




文档简介
苏科版八年级数学下册《第11章 反比例函数》章末过关达标检测
(时间:90分钟 满分:120分)
一.选择题(共19题;共38分)
1.反比例函数y=(x>0)的图象如图所示,随着x值的增大,y值( )
A.增大 B.减小 C.不变 D.先减小后增大
第1提图 第3提图 第5提图 第6提图
2.下列四个点中,有三个点在同一反比例函数y=的图象上,则不在这个函数图象上的点是( )
A.(5,1) B.(-1,5) C.(,3) D.(-3,-)
3.如图,在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线y=(x>0)上的一个动点,当点B的横坐标逐渐增大时,△OAB的面积将会( )
A.逐渐增大 B.不变
C.逐渐减小 D.先增大后减小
4.反比例函数y=的图象在每条曲线上,y随x的增大而减小,则k的值可为( )
A.-1 B.0 C.1 D.2
5.如图,正方形ABOC的边长为2,反比例函数y=过点A,则k的值是( )
A.2 B.-2 C.4 D.-4
6.如图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上.反比例函数y=(x>0)的图象经过顶点B,则k的值为( )
A.12 B.20 C.24 D.32
7.某工厂现有材料100吨,若平均每天用去x吨,这批材料能用y天,则y与x之间的函数关系式为( )
A.y=100x B.y= C.y=100- D.y=100-x
8.函数y=的图象经过的点是( )
A.(2,1) B.(2,-1) C.(2,4) D.(-,2)
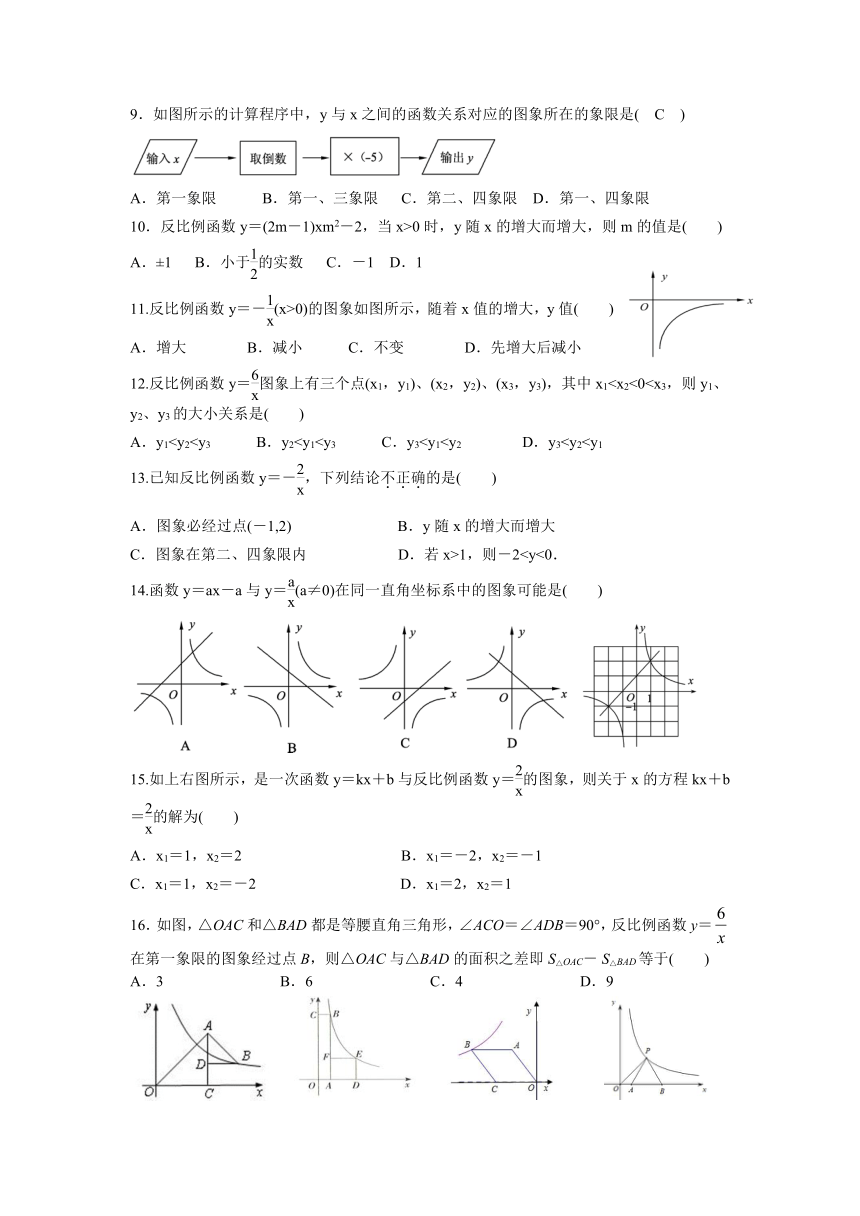
9.如图所示的计算程序中,y与x之间的函数关系对应的图象所在的象限是( C )
A.第一象限 B.第一、三象限 C.第二、四象限 D.第一、四象限
10.反比例函数y=(2m-1)xm2-2,当x>0时,y随x的增大而增大,则m的值是( )
A.±1 B.小于的实数 C.-1 D.1
11.反比例函数y=-(x>0)的图象如图所示,随着x值的增大,y值( )
A.增大 B.减小 C.不变 D.先增大后减小
12.反比例函数y=图象上有三个点(x1,y1)、(x2,y2)、(x3,y3),其中x1A.y113.已知反比例函数y=-,下列结论不正确的是( )
A.图象必经过点(-1,2) B.y随x的增大而增大
C.图象在第二、四象限内 D.若x>1,则-214.函数y=ax-a与y=(a≠0)在同一直角坐标系中的图象可能是( )
15.如上右图所示,是一次函数y=kx+b与反比例函数y=的图象,则关于x的方程kx+b=的解为( )
A.x1=1,x2=2 B.x1=-2,x2=-1
C.x1=1,x2=-2 D.x1=2,x2=1
16.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B,则△OAC与△BAD的面积之差即S△OAC-?S△BAD等于(?? )
A.3 B.6 C.4 D.9
第16题图 第17题图 第18题图 第19题图
17.如图,在平面直角坐标系中,四边形是矩形,四边形是正方形,点、在轴的正半轴上,点在轴的正半轴上,点在上,点、在函数的图象上,若正方形的面积为4,且,则的值为( )
A.24 B.12 C.6 D.3
18.如图,O为坐标原点,菱形OABC的顶点A的坐标为,顶点C在轴的负半轴上,函数的图象经过顶点B,则的值为( )
A. B. C. D.
19.如图,是反比例函数在第一象限内的图象上一点,以为顶点作等边,使落在轴上,则的面积为( )
A.4 B. C. D.
二.填空题(共10题;共20分)
20.已知一个函数的图象与y=的图象关于y轴对称,则该函数的解析式为 .
21.在对物体做功一定的情况下,力F(N)与此物体在力的方向上移动的距离s(m)成反比例函数关系,其图象如图所示,点P(5,1)在图象上,则当力达到10 N时,物体在力的方向上移动的距离是 m.
第21题图 第22题图 第25题图 第26题图 第27题图 第28题图
22.如图,点P在反比例函数y=的图象上,且PD⊥x轴于点D,连接OP,若△POD的面积为3,则k的值是 .
23.已知函数y=的图象经过点(-1,3),若点(2,m)在这个函数图象上,则m=
24.直线y=ax+b(a>0)与双曲线y=相交于A(x1,y1),B(x2,y2)两点,则x1y1+x2y2的值为 .
25.反比例函数的图象如图所示,以下结论:①常数;②在每个象限内,随的增大而增大;③若在该函数图象上,则;④若在该函数图象上,则也在该函数图象上,其中正确的是_______(写出序号).
26.如图,点是正比例函数的图象与反比例函数的图象在第二象限内的交点,交轴于点,且的面积为2,则的值是_________.
27.如图,点是正比例函数与反比例函数在第一象限内的交点,交轴于点,的面积为4,则的值是_______.
28.如图,在平面直角坐标系中,点在函数的图象上,过点分别作轴,轴的垂线,垂足分别为,,取线段的中点,连结并延长交轴于点,则的面积为______.
29.已知如图,一次函数y=ax+b和反比例函数y=的图象相交于A、B两点,不等式ax+b>的解集为_____.
三.解答题(共9小题 共62分)
30.(6分)已知直线与双曲线相交于两点,且点的横坐标为2.
求双曲线解析式和点的坐标;
(2)当时,利用函数图象直接写出的取值范围.
31.(6分)在平面直角坐标系中,反比例函数的图像与一次函数的图像相交于横坐标为的点. (1)求这个一次函数的解析式; (2)如图,已知点在这个一次函数图像上,点在反比例函数的图像上,直线轴,且在点上方,并与轴相交于点.如果点恰好是的中点,求点的坐标.
32.(6分)如图,反比例函数与一次函数的图象交于点,.
(1)求反比例函数与一次函数的解析式.(2)求△OAB的面积.
33.(6分)如图,己知反比例函数的图象与一次函数的图象在第一象限交于,两点.
(1)求反比例函数和一次函数的表达式;(2)已知点,过点作平行于轴的直线,在第一象限内交一次函数的图象于点,交反比例函数的图象于点.若,结合函数图象直接写出的取值范围.
34.(6分)工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800 ℃,然后停止煅烧进行锻造操作,经过8 min时,材料温度降为600 ℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系.(如图)已知该材料初始温度是32 ℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480 ℃时,须停止操作,那么锻造的操作时间有多长?
35.(9分)我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度18 ℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
36.(6分)如图,已知反比例函数y= 与一次函数y=k x+b的图象相交于A(4,1),B(a,2)两点,一次函数的图象与y轴的交点为C.
(1)求反比例函数和一次函数的表达式;
(2)若点D的坐标为(1,0),求△ACD的面积.
37、(9分)如图,点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点. (1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
(3)若C是x轴上一动点,设t=CB-CA,求t的最大值,并求出此时点C的坐标.
38、(8分)阅读下面材料,然后解答问题:
在平面直角坐标系中,以任意两点P(x1,y1),Q(x2,y2)为端点的线段的中点坐标为(,).如图,在平面直角坐标系xOy中,双曲线y=(x<0)和y=(x>0)的图象关于y轴对称,直线y=+与两个图象分别交于A(a,1),B(1,b)两点,点C为线段AB的中点,连接OC、OB.
(1)求a、b、k的值及点C的坐标;
(2)若在坐标平面上有一点D,使得以O、C、B、D为顶点的四边形是平行四边形,请求出点D的坐标.
教师样卷
一.选择题(共19题;共38分)
1.反比例函数y=(x>0)的图象如图所示,随着x值的增大,y值( B )
A.增大 B.减小 C.不变 D.先减小后增大
第1提图 第3提图 第5提图 第6提图
2.下列四个点中,有三个点在同一反比例函数y=的图象上,则不在这个函数图象上的点是( B )
A.(5,1) B.(-1,5) C.(,3) D.(-3,-)
3.如图,在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线y=(x>0)上的一个动点,当点B的横坐标逐渐增大时,△OAB的面积将会( C )
A.逐渐增大 B.不变
C.逐渐减小 D.先增大后减小
4.反比例函数y=的图象在每条曲线上,y随x的增大而减小,则k的值可为( D )
A.-1 B.0 C.1 D.2
5.如图,正方形ABOC的边长为2,反比例函数y=过点A,则k的值是( D )
A.2 B.-2 C.4 D.-4
6.如图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上.反比例函数y=(x>0)的图象经过顶点B,则k的值为( D )
A.12 B.20 C.24 D.32
7.某工厂现有材料100吨,若平均每天用去x吨,这批材料能用y天,则y与x之间的函数关系式为( B )
A.y=100x B.y= C.y=100- D.y=100-x
8.函数y=的图象经过的点是( A )
A.(2,1) B.(2,-1) C.(2,4) D.(-,2)
【解析】把x=2,y=1代入y=中,等式成立,故(2,1)在y=上.
9.如图所示的计算程序中,y与x之间的函数关系对应的图象所在的象限是( C )
A.第一象限 B.第一、三象限 C.第二、四象限 D.第一、四象限
【解析】由题意得y=-,所以图象在第二、四象限.
10.反比例函数y=(2m-1)xm2-2,当x>0时,y随x的增大而增大,则m的值是( C )
A.±1 B.小于的实数 C.-1 D.1
【解析】由题意得解得m=-1.
11.反比例函数y=-(x>0)的图象如图所示,随着x值的增大,y值( A )
A.增大 B.减小 C.不变 D.先增大后减小
【解析】∵k=-1<0,∴y随着x的增大而增大.
12.反比例函数y=图象上有三个点(x1,y1)、(x2,y2)、(x3,y3),其中x1A.y1【解析】∵y=,∴k=6>0,∴图象在每个象限内y随x的增大而减小.∵x1y2,∴y213.已知反比例函数y=-,下列结论不正确的是( B )
A.图象必经过点(-1,2) B.y随x的增大而增大
C.图象在第二、四象限内 D.若x>1,则-2【解析】∵k=-2<0,∴在每个象限内y随x的增大而增大.
14.函数y=ax-a与y=(a≠0)在同一直角坐标系中的图象可能是( D )
【解析】当a<0时,y=的分支在第二、四象限,y=ax-a经过第一、二、四象限.
15.如图所示,是一次函数y=kx+b与反比例函数y=的图象,则关于x的方程kx+b=的解为( C )
A.x1=1,x2=2 B.x1=-2,x2=-1
C.x1=1,x2=-2 D.x1=2,x2=1
【解析】y=kx+b与y=图象的交点横坐标即为kx+b=的解,由图象可得x1=1,x2=-2.
16.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B,则△OAC与△BAD的面积之差即S△OAC-?S△BAD等于(?? A )
A.3 B.6 C.4 D.9
解:设△OAC和△BAD的直角边长分别为a、b,则点B的坐标为(a+b,a﹣b).∵点B在反比例函数y=的第一象限图象上,∴(a+b)(a﹣b)=a2﹣b2=6.∴S△OAC﹣S△BAD=a2﹣b2=(a2﹣b2)=×6=3.故选A.
第16题图 第17题图 第18题图 第19题图
17.如图,在平面直角坐标系中,四边形是矩形,四边形是正方形,点、在轴的正半轴上,点在轴的正半轴上,点在上,点、在函数的图象上,若正方形的面积为4,且,则的值为( C )
A.24 B.12 C.6 D.3
解:∵正方形ADEF的面积为4,∴正方形ADEF的边长为2,∴BF=2AF=4,AB=AF+BF=2+4=6.设B点坐标为(t,6),则E点坐标(t+2,2),∵点B、E在反比例函数y=的图象上,∴k=6t=2(t+2),解得t=1,k=6.故选:C.
18.如图,O为坐标原点,菱形OABC的顶点A的坐标为,顶点C在轴的负半轴上,函数的图象经过顶点B,则的值为( C )
A. B. C. D.
【解析】∵A(﹣3,4),∴OA==5,∵四边形OABC是菱形,∴AO=CB=OC=AB=5,则点B的横坐标为﹣3﹣5=﹣8,故B的坐标为:(﹣8,4),
将点B的坐标代入得,4=,解得:k=﹣32.故选C.
19.如图,是反比例函数在第一象限内的图象上一点,以为顶点作等边,使落在轴上,则的面积为( C )
A.4 B. C. D.
解:如图,作PD⊥OB,∵P(m,m)是反比例函数在第一象限内的图象上一点,∴,解得:m=,∴PD=OD=,
∵△ABP是等边三角形,∴BD=,∴S△POB=OB?PD=(OD+BD)?PD=;故选:C.
二.填空题(共10题;共20分)
20.已知一个函数的图象与y=的图象关于y轴对称,则该函数的解析式为 .
【答案】.y=-
21.在对物体做功一定的情况下,力F(N)与此物体在力的方向上移动的距离s(m)成反比例函数关系,其图象如图所示,点P(5,1)在图象上,则当力达到10 N时,物体在力的方向上移动的距离是 m.
【答案】1.2
第21题图 第22题图 第25题图 第26题图 第27题图 第28题图
22.如图,点P在反比例函数y=的图象上,且PD⊥x轴于点D,连接OP,若△POD的面积为3,则k的值是 .
【答案】-6
23.已知函数y=的图象经过点(-1,3),若点(2,m)在这个函数图象上,则m= .
【答案】-
24.直线y=ax+b(a>0)与双曲线y=相交于A(x1,y1),B(x2,y2)两点,则x1y1+x2y2的值为 .
【答案】6
25.反比例函数的图象如图所示,以下结论:①常数;②在每个象限内,随的增大而增大;③若在该函数图象上,则;④若在该函数图象上,则也在该函数图象上,其中正确的是_______(写出序号).
【答案】③④ 解:∵反比例函数的图象位于一三象限,∴m>0故①错误;当反比例函数的图象位于一三象限时,在每一象限内,y随x的增大而减小,故②错误;将A(-1,h),B(2,k)代入,得到h=-m,2k=m,∵m>0∴h<k,故③正确;将P(x,y)代入得到m=xy,将P′(-x,-y)代入得到m=xy,故P(x,y)在图象上,则P′(-x,-y)也在图象上,故④正确,故答案为:③④.
26.如图,点是正比例函数的图象与反比例函数的图象在第二象限内的交点,交轴于点,且的面积为2,则的值是_________.
【答案】-2 解:过P作PC⊥OA于点C,∵P点在y=-x上,∴∠POA=45°,又PA⊥PO,∴△POA为等腰直角三角形,过P作PC⊥OA于C,则S△POC=S△PCA=,∴S△POA==2,∴k=-2,故答案为:-2.
27.如图,点是正比例函数与反比例函数在第一象限内的交点,交轴于点,的面积为4,则的值是_______.
【答案】4 解:过作于,如图,正比例函数的解析式为,,,为等腰直角三角形,,,,.故答案为4.
28.如图,在平面直角坐标系中,点在函数的图象上,过点分别作轴,轴的垂线,垂足分别为,,取线段的中点,连结并延长交轴于点,则的面积为______.
【答案】9【解析】解:∵PB⊥y轴,PA⊥x轴,∴S矩形APBO=9,∵C点为OB的中点,∴OC=BC,
在△PBC和△DOC中,∴△PBC≌△DOC,∴S△PBC=S△DOC,∴S△APD=S矩形APBO=9.故答案为9.
29.已知如图,一次函数y=ax+b和反比例函数y=的图象相交于A、B两点,不等式ax+b>的解集为_____.
【答案】x>1或﹣3<x<0.解:观察函数图象,当x>1或﹣3<x<0时,ax+b>,
故答案为x>1或﹣3<x<0.
三.解答题(共9小题 共62分)
30.(6分)已知直线与双曲线相交于两点,且点的横坐标为2.
求双曲线解析式和点的坐标;
(2)当时,利用函数图象直接写出的取值范围.
解:(1)把代入得:,即点的坐标为:,将点A的坐标为(2,1)代入中,可得k=2,双曲线解析式为.点和点关于原点中心对称,
点的坐标为:,
(2)根据图象可知:的取值范围为:或.
31.(6分)在平面直角坐标系中,反比例函数的图像与一次函数的图像相交于横坐标为的点. (1)求这个一次函数的解析式; (2)如图,已知点在这个一次函数图像上,点在反比例函数的图像上,直线轴,且在点上方,并与轴相交于点.如果点恰好是的中点,求点的坐标.
解:(1)点在反比例函数图像上且横坐标为,则,由题意,得,
,一次函数解析式;
(2)设,,又点在一次函数图像上,,解得或(舍去)..
32.(6分)如图,反比例函数与一次函数的图象交于点,.
(1)求反比例函数与一次函数的解析式.(2)求△OAB的面积.
解(1)∵反比例函数过点A(,8),∴将点A代入反比例函数即: 解得:a=4,∴反比例函数解析式为:∵点B(m,2)在反比例函数上∴ ,解得m=2,
∴点B(2,2),将A(,8),B(2,2),代入一次函数中, 解得
∴一次函数解析式为:
(2)设一次函数与x轴的交点为C点,∴ C(2.5,0)∴ , ∴ ∴ n=18或n=2
33.(6分)如图,己知反比例函数的图象与一次函数的图象在第一象限交于,两点.
(1)求反比例函数和一次函数的表达式;(2)已知点,过点作平行于轴的直线,在第一象限内交一次函数的图象于点,交反比例函数的图象于点.若,结合函数图象直接写出的取值范围.
解(1)把代入,∴,∴,∴反比例函数解析式为,把,代入,,∴,∴一次函数解析式为.(2)由图象可知:当时,.
34.(6分)工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800 ℃,然后停止煅烧进行锻造操作,经过8 min时,材料温度降为600 ℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系.(如图)已知该材料初始温度是32 ℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480 ℃时,须停止操作,那么锻造的操作时间有多长?
解:(1)停止加热时,设y=(k≠0),由题意,得600=,解得k=4 800.当y=800时,=800,解得x=6,所以点B的坐标为(6,800).材料加热时,设y=ax+32(a≠0),
由题意,得800=6a+32,解得a=128.所以材料加热时,y与x的函数关系式为y=128x+32(0≤x≤6).所以停止加热进行锻造操作时,y与x的函数关系式为y=(6(2)把y=480代入y=4,得x=10,10-6=4(分).答:锻造操作的时间为4分钟.
35.(9分)我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度18 ℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
解:(1)恒温系统在这天保持大棚温度18 ℃的时间为10小时.
(2)因为点B(12,18)在双曲线y=上,所以18=.所以k=216.
(3)当x=16时,y==13.5.所以当x=16时,大棚内的温度约为13.5 ℃.
36.(6分)如图,已知反比例函数y= 与一次函数y=k x+b的图象相交于A(4,1),B(a,2)两点,一次函数的图象与y轴的交点为C.
(1)求反比例函数和一次函数的表达式;
(2)若点D的坐标为(1,0),求△ACD的面积.
解:(1)根据题意有m=4×1=4,B(a,2)又在y=上,所以B(2,2).根据题意有,解得.所以反比例函数表达式为y=,一次函数表达式为y=-x+3.
(2)易知C(0,3),过点A作AE⊥x轴交x轴于点E.
S梯形OCAE=×4=8,S△OCD=×3×1=,S△ADE=×(4-1)×1=,
S△ACD=S梯形OCAE-S△OCD-S△ADE=5.
37、(9分)如图,点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点. (1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
(3)若C是x轴上一动点,设t=CB-CA,求t的最大值,并求出此时点C的坐标.
解:(1)∵点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点,∴m=-2,∴反比例函数解析式为,∴n=1,∴点A(-2,1),
将点A(-2,1),B(1,-2)代入y=kx+b,得
∴一次函数的解析式为y=-x-1;
(2)结合图象知:当-2<x<0或x>1时,一次函数的值小于反比例函数的值;
(3)如解图,作点A关于x轴的对称点A′,连接BA′延长交x轴于点C,则点C即为所求,
∵A(-2,1),∴A′(-2,-1),设直线A′B的解析式为y=mx+n,
∴y=-x-,
令y=0,得x=-5,则C点坐标为(-5,0),
∴t的最大值为A′B==.
38、(8分)阅读下面材料,然后解答问题:
在平面直角坐标系中,以任意两点P(x1,y1),Q(x2,y2)为端点的线段的中点坐标为(,).如图,在平面直角坐标系xOy中,双曲线y=(x<0)和y=(x>0)的图象关于y轴对称,直线y=+与两个图象分别交于A(a,1),B(1,b)两点,点C为线段AB的中点,连接OC、OB.
(1)求a、b、k的值及点C的坐标;
(2)若在坐标平面上有一点D,使得以O、C、B、D为顶点的四边形是平行四边形,请求出点D的坐标.
解:(1)依题意得,解得,∴A(﹣3,1),B(1,3),
∵点B在双曲线y=(x>0)上,∴k=1×3=3,∵点C为线段AB的中点,∴点C坐标为(,),即为(﹣1,2);
(2)将线段OC平移,使点O(0,0)移到点B(1,3),则点C(﹣1,2)移到点D(0,5),此时四边形OCDB是平行四边形;
将线段OC平移,使点C(﹣1,2)移到点B(1,3),则点O(0,0)移到点D(2,1),此时四边形OCBD是平行四边形;
线段BO平移,使点B(1,3)移到点C(﹣1,2),则点O(0,0)移到点D(﹣2,﹣1),此时四边形BODC是平行四边形.
综上所述,符合条件的点D坐标为(0,5)或(2,1)或(﹣2,﹣1).
(时间:90分钟 满分:120分)
一.选择题(共19题;共38分)
1.反比例函数y=(x>0)的图象如图所示,随着x值的增大,y值( )
A.增大 B.减小 C.不变 D.先减小后增大
第1提图 第3提图 第5提图 第6提图
2.下列四个点中,有三个点在同一反比例函数y=的图象上,则不在这个函数图象上的点是( )
A.(5,1) B.(-1,5) C.(,3) D.(-3,-)
3.如图,在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线y=(x>0)上的一个动点,当点B的横坐标逐渐增大时,△OAB的面积将会( )
A.逐渐增大 B.不变
C.逐渐减小 D.先增大后减小
4.反比例函数y=的图象在每条曲线上,y随x的增大而减小,则k的值可为( )
A.-1 B.0 C.1 D.2
5.如图,正方形ABOC的边长为2,反比例函数y=过点A,则k的值是( )
A.2 B.-2 C.4 D.-4
6.如图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上.反比例函数y=(x>0)的图象经过顶点B,则k的值为( )
A.12 B.20 C.24 D.32
7.某工厂现有材料100吨,若平均每天用去x吨,这批材料能用y天,则y与x之间的函数关系式为( )
A.y=100x B.y= C.y=100- D.y=100-x
8.函数y=的图象经过的点是( )
A.(2,1) B.(2,-1) C.(2,4) D.(-,2)
9.如图所示的计算程序中,y与x之间的函数关系对应的图象所在的象限是( C )
A.第一象限 B.第一、三象限 C.第二、四象限 D.第一、四象限
10.反比例函数y=(2m-1)xm2-2,当x>0时,y随x的增大而增大,则m的值是( )
A.±1 B.小于的实数 C.-1 D.1
11.反比例函数y=-(x>0)的图象如图所示,随着x值的增大,y值( )
A.增大 B.减小 C.不变 D.先增大后减小
12.反比例函数y=图象上有三个点(x1,y1)、(x2,y2)、(x3,y3),其中x1
A.图象必经过点(-1,2) B.y随x的增大而增大
C.图象在第二、四象限内 D.若x>1,则-2
15.如上右图所示,是一次函数y=kx+b与反比例函数y=的图象,则关于x的方程kx+b=的解为( )
A.x1=1,x2=2 B.x1=-2,x2=-1
C.x1=1,x2=-2 D.x1=2,x2=1
16.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B,则△OAC与△BAD的面积之差即S△OAC-?S△BAD等于(?? )
A.3 B.6 C.4 D.9
第16题图 第17题图 第18题图 第19题图
17.如图,在平面直角坐标系中,四边形是矩形,四边形是正方形,点、在轴的正半轴上,点在轴的正半轴上,点在上,点、在函数的图象上,若正方形的面积为4,且,则的值为( )
A.24 B.12 C.6 D.3
18.如图,O为坐标原点,菱形OABC的顶点A的坐标为,顶点C在轴的负半轴上,函数的图象经过顶点B,则的值为( )
A. B. C. D.
19.如图,是反比例函数在第一象限内的图象上一点,以为顶点作等边,使落在轴上,则的面积为( )
A.4 B. C. D.
二.填空题(共10题;共20分)
20.已知一个函数的图象与y=的图象关于y轴对称,则该函数的解析式为 .
21.在对物体做功一定的情况下,力F(N)与此物体在力的方向上移动的距离s(m)成反比例函数关系,其图象如图所示,点P(5,1)在图象上,则当力达到10 N时,物体在力的方向上移动的距离是 m.
第21题图 第22题图 第25题图 第26题图 第27题图 第28题图
22.如图,点P在反比例函数y=的图象上,且PD⊥x轴于点D,连接OP,若△POD的面积为3,则k的值是 .
23.已知函数y=的图象经过点(-1,3),若点(2,m)在这个函数图象上,则m=
24.直线y=ax+b(a>0)与双曲线y=相交于A(x1,y1),B(x2,y2)两点,则x1y1+x2y2的值为 .
25.反比例函数的图象如图所示,以下结论:①常数;②在每个象限内,随的增大而增大;③若在该函数图象上,则;④若在该函数图象上,则也在该函数图象上,其中正确的是_______(写出序号).
26.如图,点是正比例函数的图象与反比例函数的图象在第二象限内的交点,交轴于点,且的面积为2,则的值是_________.
27.如图,点是正比例函数与反比例函数在第一象限内的交点,交轴于点,的面积为4,则的值是_______.
28.如图,在平面直角坐标系中,点在函数的图象上,过点分别作轴,轴的垂线,垂足分别为,,取线段的中点,连结并延长交轴于点,则的面积为______.
29.已知如图,一次函数y=ax+b和反比例函数y=的图象相交于A、B两点,不等式ax+b>的解集为_____.
三.解答题(共9小题 共62分)
30.(6分)已知直线与双曲线相交于两点,且点的横坐标为2.
求双曲线解析式和点的坐标;
(2)当时,利用函数图象直接写出的取值范围.
31.(6分)在平面直角坐标系中,反比例函数的图像与一次函数的图像相交于横坐标为的点. (1)求这个一次函数的解析式; (2)如图,已知点在这个一次函数图像上,点在反比例函数的图像上,直线轴,且在点上方,并与轴相交于点.如果点恰好是的中点,求点的坐标.
32.(6分)如图,反比例函数与一次函数的图象交于点,.
(1)求反比例函数与一次函数的解析式.(2)求△OAB的面积.
33.(6分)如图,己知反比例函数的图象与一次函数的图象在第一象限交于,两点.
(1)求反比例函数和一次函数的表达式;(2)已知点,过点作平行于轴的直线,在第一象限内交一次函数的图象于点,交反比例函数的图象于点.若,结合函数图象直接写出的取值范围.
34.(6分)工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800 ℃,然后停止煅烧进行锻造操作,经过8 min时,材料温度降为600 ℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系.(如图)已知该材料初始温度是32 ℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480 ℃时,须停止操作,那么锻造的操作时间有多长?
35.(9分)我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度18 ℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
36.(6分)如图,已知反比例函数y= 与一次函数y=k x+b的图象相交于A(4,1),B(a,2)两点,一次函数的图象与y轴的交点为C.
(1)求反比例函数和一次函数的表达式;
(2)若点D的坐标为(1,0),求△ACD的面积.
37、(9分)如图,点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点. (1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
(3)若C是x轴上一动点,设t=CB-CA,求t的最大值,并求出此时点C的坐标.
38、(8分)阅读下面材料,然后解答问题:
在平面直角坐标系中,以任意两点P(x1,y1),Q(x2,y2)为端点的线段的中点坐标为(,).如图,在平面直角坐标系xOy中,双曲线y=(x<0)和y=(x>0)的图象关于y轴对称,直线y=+与两个图象分别交于A(a,1),B(1,b)两点,点C为线段AB的中点,连接OC、OB.
(1)求a、b、k的值及点C的坐标;
(2)若在坐标平面上有一点D,使得以O、C、B、D为顶点的四边形是平行四边形,请求出点D的坐标.
教师样卷
一.选择题(共19题;共38分)
1.反比例函数y=(x>0)的图象如图所示,随着x值的增大,y值( B )
A.增大 B.减小 C.不变 D.先减小后增大
第1提图 第3提图 第5提图 第6提图
2.下列四个点中,有三个点在同一反比例函数y=的图象上,则不在这个函数图象上的点是( B )
A.(5,1) B.(-1,5) C.(,3) D.(-3,-)
3.如图,在直角坐标系中,点A是x轴正半轴上的一个定点,点B是双曲线y=(x>0)上的一个动点,当点B的横坐标逐渐增大时,△OAB的面积将会( C )
A.逐渐增大 B.不变
C.逐渐减小 D.先增大后减小
4.反比例函数y=的图象在每条曲线上,y随x的增大而减小,则k的值可为( D )
A.-1 B.0 C.1 D.2
5.如图,正方形ABOC的边长为2,反比例函数y=过点A,则k的值是( D )
A.2 B.-2 C.4 D.-4
6.如图,菱形OABC的顶点C的坐标为(3,4),顶点A在x轴的正半轴上.反比例函数y=(x>0)的图象经过顶点B,则k的值为( D )
A.12 B.20 C.24 D.32
7.某工厂现有材料100吨,若平均每天用去x吨,这批材料能用y天,则y与x之间的函数关系式为( B )
A.y=100x B.y= C.y=100- D.y=100-x
8.函数y=的图象经过的点是( A )
A.(2,1) B.(2,-1) C.(2,4) D.(-,2)
【解析】把x=2,y=1代入y=中,等式成立,故(2,1)在y=上.
9.如图所示的计算程序中,y与x之间的函数关系对应的图象所在的象限是( C )
A.第一象限 B.第一、三象限 C.第二、四象限 D.第一、四象限
【解析】由题意得y=-,所以图象在第二、四象限.
10.反比例函数y=(2m-1)xm2-2,当x>0时,y随x的增大而增大,则m的值是( C )
A.±1 B.小于的实数 C.-1 D.1
【解析】由题意得解得m=-1.
11.反比例函数y=-(x>0)的图象如图所示,随着x值的增大,y值( A )
A.增大 B.减小 C.不变 D.先增大后减小
【解析】∵k=-1<0,∴y随着x的增大而增大.
12.反比例函数y=图象上有三个点(x1,y1)、(x2,y2)、(x3,y3),其中x1
A.图象必经过点(-1,2) B.y随x的增大而增大
C.图象在第二、四象限内 D.若x>1,则-2
14.函数y=ax-a与y=(a≠0)在同一直角坐标系中的图象可能是( D )
【解析】当a<0时,y=的分支在第二、四象限,y=ax-a经过第一、二、四象限.
15.如图所示,是一次函数y=kx+b与反比例函数y=的图象,则关于x的方程kx+b=的解为( C )
A.x1=1,x2=2 B.x1=-2,x2=-1
C.x1=1,x2=-2 D.x1=2,x2=1
【解析】y=kx+b与y=图象的交点横坐标即为kx+b=的解,由图象可得x1=1,x2=-2.
16.如图,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函数y=在第一象限的图象经过点B,则△OAC与△BAD的面积之差即S△OAC-?S△BAD等于(?? A )
A.3 B.6 C.4 D.9
解:设△OAC和△BAD的直角边长分别为a、b,则点B的坐标为(a+b,a﹣b).∵点B在反比例函数y=的第一象限图象上,∴(a+b)(a﹣b)=a2﹣b2=6.∴S△OAC﹣S△BAD=a2﹣b2=(a2﹣b2)=×6=3.故选A.
第16题图 第17题图 第18题图 第19题图
17.如图,在平面直角坐标系中,四边形是矩形,四边形是正方形,点、在轴的正半轴上,点在轴的正半轴上,点在上,点、在函数的图象上,若正方形的面积为4,且,则的值为( C )
A.24 B.12 C.6 D.3
解:∵正方形ADEF的面积为4,∴正方形ADEF的边长为2,∴BF=2AF=4,AB=AF+BF=2+4=6.设B点坐标为(t,6),则E点坐标(t+2,2),∵点B、E在反比例函数y=的图象上,∴k=6t=2(t+2),解得t=1,k=6.故选:C.
18.如图,O为坐标原点,菱形OABC的顶点A的坐标为,顶点C在轴的负半轴上,函数的图象经过顶点B,则的值为( C )
A. B. C. D.
【解析】∵A(﹣3,4),∴OA==5,∵四边形OABC是菱形,∴AO=CB=OC=AB=5,则点B的横坐标为﹣3﹣5=﹣8,故B的坐标为:(﹣8,4),
将点B的坐标代入得,4=,解得:k=﹣32.故选C.
19.如图,是反比例函数在第一象限内的图象上一点,以为顶点作等边,使落在轴上,则的面积为( C )
A.4 B. C. D.
解:如图,作PD⊥OB,∵P(m,m)是反比例函数在第一象限内的图象上一点,∴,解得:m=,∴PD=OD=,
∵△ABP是等边三角形,∴BD=,∴S△POB=OB?PD=(OD+BD)?PD=;故选:C.
二.填空题(共10题;共20分)
20.已知一个函数的图象与y=的图象关于y轴对称,则该函数的解析式为 .
【答案】.y=-
21.在对物体做功一定的情况下,力F(N)与此物体在力的方向上移动的距离s(m)成反比例函数关系,其图象如图所示,点P(5,1)在图象上,则当力达到10 N时,物体在力的方向上移动的距离是 m.
【答案】1.2
第21题图 第22题图 第25题图 第26题图 第27题图 第28题图
22.如图,点P在反比例函数y=的图象上,且PD⊥x轴于点D,连接OP,若△POD的面积为3,则k的值是 .
【答案】-6
23.已知函数y=的图象经过点(-1,3),若点(2,m)在这个函数图象上,则m= .
【答案】-
24.直线y=ax+b(a>0)与双曲线y=相交于A(x1,y1),B(x2,y2)两点,则x1y1+x2y2的值为 .
【答案】6
25.反比例函数的图象如图所示,以下结论:①常数;②在每个象限内,随的增大而增大;③若在该函数图象上,则;④若在该函数图象上,则也在该函数图象上,其中正确的是_______(写出序号).
【答案】③④ 解:∵反比例函数的图象位于一三象限,∴m>0故①错误;当反比例函数的图象位于一三象限时,在每一象限内,y随x的增大而减小,故②错误;将A(-1,h),B(2,k)代入,得到h=-m,2k=m,∵m>0∴h<k,故③正确;将P(x,y)代入得到m=xy,将P′(-x,-y)代入得到m=xy,故P(x,y)在图象上,则P′(-x,-y)也在图象上,故④正确,故答案为:③④.
26.如图,点是正比例函数的图象与反比例函数的图象在第二象限内的交点,交轴于点,且的面积为2,则的值是_________.
【答案】-2 解:过P作PC⊥OA于点C,∵P点在y=-x上,∴∠POA=45°,又PA⊥PO,∴△POA为等腰直角三角形,过P作PC⊥OA于C,则S△POC=S△PCA=,∴S△POA==2,∴k=-2,故答案为:-2.
27.如图,点是正比例函数与反比例函数在第一象限内的交点,交轴于点,的面积为4,则的值是_______.
【答案】4 解:过作于,如图,正比例函数的解析式为,,,为等腰直角三角形,,,,.故答案为4.
28.如图,在平面直角坐标系中,点在函数的图象上,过点分别作轴,轴的垂线,垂足分别为,,取线段的中点,连结并延长交轴于点,则的面积为______.
【答案】9【解析】解:∵PB⊥y轴,PA⊥x轴,∴S矩形APBO=9,∵C点为OB的中点,∴OC=BC,
在△PBC和△DOC中,∴△PBC≌△DOC,∴S△PBC=S△DOC,∴S△APD=S矩形APBO=9.故答案为9.
29.已知如图,一次函数y=ax+b和反比例函数y=的图象相交于A、B两点,不等式ax+b>的解集为_____.
【答案】x>1或﹣3<x<0.解:观察函数图象,当x>1或﹣3<x<0时,ax+b>,
故答案为x>1或﹣3<x<0.
三.解答题(共9小题 共62分)
30.(6分)已知直线与双曲线相交于两点,且点的横坐标为2.
求双曲线解析式和点的坐标;
(2)当时,利用函数图象直接写出的取值范围.
解:(1)把代入得:,即点的坐标为:,将点A的坐标为(2,1)代入中,可得k=2,双曲线解析式为.点和点关于原点中心对称,
点的坐标为:,
(2)根据图象可知:的取值范围为:或.
31.(6分)在平面直角坐标系中,反比例函数的图像与一次函数的图像相交于横坐标为的点. (1)求这个一次函数的解析式; (2)如图,已知点在这个一次函数图像上,点在反比例函数的图像上,直线轴,且在点上方,并与轴相交于点.如果点恰好是的中点,求点的坐标.
解:(1)点在反比例函数图像上且横坐标为,则,由题意,得,
,一次函数解析式;
(2)设,,又点在一次函数图像上,,解得或(舍去)..
32.(6分)如图,反比例函数与一次函数的图象交于点,.
(1)求反比例函数与一次函数的解析式.(2)求△OAB的面积.
解(1)∵反比例函数过点A(,8),∴将点A代入反比例函数即: 解得:a=4,∴反比例函数解析式为:∵点B(m,2)在反比例函数上∴ ,解得m=2,
∴点B(2,2),将A(,8),B(2,2),代入一次函数中, 解得
∴一次函数解析式为:
(2)设一次函数与x轴的交点为C点,∴ C(2.5,0)∴ , ∴ ∴ n=18或n=2
33.(6分)如图,己知反比例函数的图象与一次函数的图象在第一象限交于,两点.
(1)求反比例函数和一次函数的表达式;(2)已知点,过点作平行于轴的直线,在第一象限内交一次函数的图象于点,交反比例函数的图象于点.若,结合函数图象直接写出的取值范围.
解(1)把代入,∴,∴,∴反比例函数解析式为,把,代入,,∴,∴一次函数解析式为.(2)由图象可知:当时,.
34.(6分)工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800 ℃,然后停止煅烧进行锻造操作,经过8 min时,材料温度降为600 ℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系.(如图)已知该材料初始温度是32 ℃.
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480 ℃时,须停止操作,那么锻造的操作时间有多长?
解:(1)停止加热时,设y=(k≠0),由题意,得600=,解得k=4 800.当y=800时,=800,解得x=6,所以点B的坐标为(6,800).材料加热时,设y=ax+32(a≠0),
由题意,得800=6a+32,解得a=128.所以材料加热时,y与x的函数关系式为y=128x+32(0≤x≤6).所以停止加热进行锻造操作时,y与x的函数关系式为y=(6
35.(9分)我市某蔬菜生产基地在气温较低时,用装有恒温系统的大棚栽培一种在自然光照且温度为18 ℃的条件下生长最快的新品种.如图是某天恒温系统从开启到关闭及关闭后,大棚内温度y(℃)随时间x(小时)变化的函数图象,其中BC段是双曲线y=的一部分.请根据图中信息解答下列问题:
(1)恒温系统在这天保持大棚内温度18 ℃的时间有多少小时?
(2)求k的值;
(3)当x=16时,大棚内的温度约为多少度?
解:(1)恒温系统在这天保持大棚温度18 ℃的时间为10小时.
(2)因为点B(12,18)在双曲线y=上,所以18=.所以k=216.
(3)当x=16时,y==13.5.所以当x=16时,大棚内的温度约为13.5 ℃.
36.(6分)如图,已知反比例函数y= 与一次函数y=k x+b的图象相交于A(4,1),B(a,2)两点,一次函数的图象与y轴的交点为C.
(1)求反比例函数和一次函数的表达式;
(2)若点D的坐标为(1,0),求△ACD的面积.
解:(1)根据题意有m=4×1=4,B(a,2)又在y=上,所以B(2,2).根据题意有,解得.所以反比例函数表达式为y=,一次函数表达式为y=-x+3.
(2)易知C(0,3),过点A作AE⊥x轴交x轴于点E.
S梯形OCAE=×4=8,S△OCD=×3×1=,S△ADE=×(4-1)×1=,
S△ACD=S梯形OCAE-S△OCD-S△ADE=5.
37、(9分)如图,点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点. (1)求反比例函数和一次函数的解析式;
(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围;
(3)若C是x轴上一动点,设t=CB-CA,求t的最大值,并求出此时点C的坐标.
解:(1)∵点A(-2,n),B(1,-2)是一次函数y=kx+b的图象和反比例函数y=的图象的两个交点,∴m=-2,∴反比例函数解析式为,∴n=1,∴点A(-2,1),
将点A(-2,1),B(1,-2)代入y=kx+b,得
∴一次函数的解析式为y=-x-1;
(2)结合图象知:当-2<x<0或x>1时,一次函数的值小于反比例函数的值;
(3)如解图,作点A关于x轴的对称点A′,连接BA′延长交x轴于点C,则点C即为所求,
∵A(-2,1),∴A′(-2,-1),设直线A′B的解析式为y=mx+n,
∴y=-x-,
令y=0,得x=-5,则C点坐标为(-5,0),
∴t的最大值为A′B==.
38、(8分)阅读下面材料,然后解答问题:
在平面直角坐标系中,以任意两点P(x1,y1),Q(x2,y2)为端点的线段的中点坐标为(,).如图,在平面直角坐标系xOy中,双曲线y=(x<0)和y=(x>0)的图象关于y轴对称,直线y=+与两个图象分别交于A(a,1),B(1,b)两点,点C为线段AB的中点,连接OC、OB.
(1)求a、b、k的值及点C的坐标;
(2)若在坐标平面上有一点D,使得以O、C、B、D为顶点的四边形是平行四边形,请求出点D的坐标.
解:(1)依题意得,解得,∴A(﹣3,1),B(1,3),
∵点B在双曲线y=(x>0)上,∴k=1×3=3,∵点C为线段AB的中点,∴点C坐标为(,),即为(﹣1,2);
(2)将线段OC平移,使点O(0,0)移到点B(1,3),则点C(﹣1,2)移到点D(0,5),此时四边形OCDB是平行四边形;
将线段OC平移,使点C(﹣1,2)移到点B(1,3),则点O(0,0)移到点D(2,1),此时四边形OCBD是平行四边形;
线段BO平移,使点B(1,3)移到点C(﹣1,2),则点O(0,0)移到点D(﹣2,﹣1),此时四边形BODC是平行四边形.
综上所述,符合条件的点D坐标为(0,5)或(2,1)或(﹣2,﹣1).
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
