2012年中考复习专题一实数

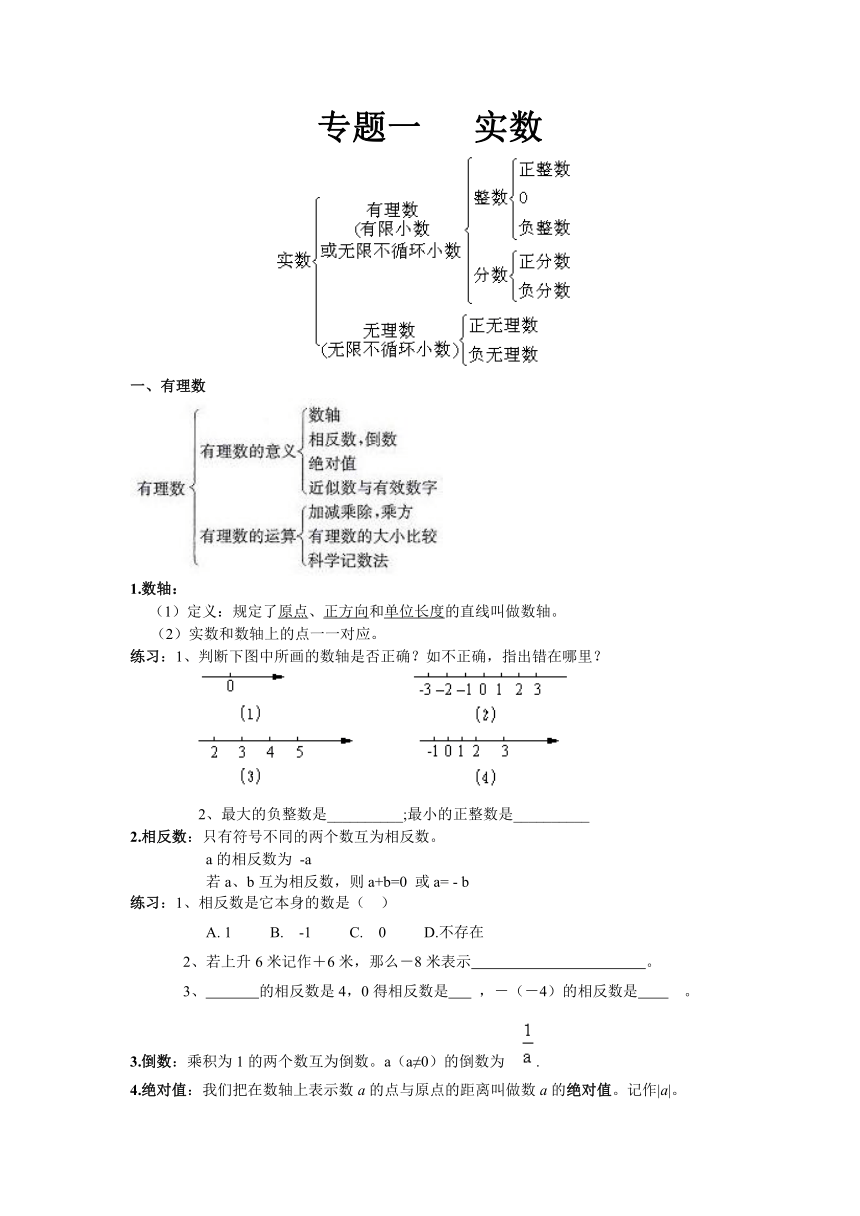
专题一 实数
一、有理数
1.数轴：
（1）定义：规定了原点、正方向和单位长度的直线叫做数轴。
（2）实数和数轴上的点一一对应。
练习：1、判断下图中所画的数轴是否正确？如不正确，指出错在哪里？
2、最大的负整数是__________;最小的正整数是__________
2.相反数：只有符号不同的两个数互为相反数。
a的相反数为 -a
若a、b互为相反数，则a+b=0 或a= - b
练习：1、相反数是它本身的数是（ ）
A. 1 B. -1 C. 0 D.不存在
2、若上升6米记作＋6米，那么－8米表示 。
3、 的相反数是4，0得相反数是 ，－（－4）的相反数是 。
3.倒数：乘积为1的两个数互为倒数。a（a≠0）的倒数为 .
4.绝对值：我们把在数轴上表示数a的点与原点的距离叫做数a的绝对值。记作|a|。
（3）有关性质
a） 互为相反数的两个数的绝对值相等 即
b）任何数的绝对值为非负数
c）任何数的绝对值都不小于它本身
d）且
练习：1、下列各式中，等号成立的是（ ）
A、－=6 B、=－6 C、－=－1 D、=－3.14
2、在数轴上表示的数8与－2这两个点之间的距离是 （ ）
A、6 B、10 C、-10 D-6
3、一个有理数的绝对值等于其本身，这个数是 （ ）
A、正数 B、非负数 C、零 D、负数
4、绝对值最小的数是 ，－3的绝对值是 。
5.实数的大小比较
（1）正数>0；负数<0；正数>负数；两个正数，绝对值大的正数大；两个负数，绝对值大的反而小。
（2）用数轴比较： 右边的数大于左边的数。
练习：5、2.5、、―4、3.25、、―4、0、1各数用数轴上的点表示出来，并用“＜”号连接起来。
6.科学记数法、近似数和有效数字。
（1）科学记数法：一般地，把一个大于10的数记成a×的形式，其中a 是整数数位只有一位的数（即1≤a<10），n是正整数，这种记数法叫做科学记数法。
练习：用科学记数法记出下列各数：
(1)696 000； (2)1 000 000； (3)58 000； (4)―7 800 000。
（2）近似数
（3）有效数字：从左边第一个不是0的数字起，到精确到的数位止，所有的数字，都叫做这个数字的有效数字。
练习：例1：下列由四舍五入法得到的近似数，各精确到哪一位 各有哪几个有效数字
(1)132.4； (2)0.0572； (3)2.40万
例2：用四舍五入法，按括号中的要求把下列各数取近似数。
(1)0.34082(精确到千分位)；
(2)64.8 (精确到个位)；
(3)1.504 (精确到0.01)；
(4)0.0692 (保留2个有效数字)；
(5)30542 (保留3个有效数字)。
7.实数的运算
加法：①有理数加法法则：
（a）同号两数相加，取相同的符号，并把绝对值相加
（b）异号两数相加，
若绝对值不等，取绝对值较大的符号，并用较大的绝对值减去较小的绝对值
互为相反数的两个数相加得0
（c）一个数同0相加，仍得这个数。
练习：（1）（＋5）＋（＋6）
（2）（－17）＋（－29）
（3）（＋4）＋（－21）
（4）（－10）＋（＋10）
（5）（－7）＋0
（1）
（2）
（3）
②有理数的加法运算律
交换律：a＋b＝b＋a
结合律：（a＋b）＋c ＝a＋（b＋c）
计算
16＋（－25）＋24＋（－35）
（2）
（3）10袋小麦称重记录如下：
107，105，96，106，104，103，97，98，108，101
求这10袋小麦的总重量和平均重量是多少？
减法：有理数减法法则:减去一个数，等于加上这个数的相反数。表示为：a – b = a +（―b）。
计算：
(1)(―32)―(+5)； (2)7.3―(―6.8)； (3)(―2)―(―25)； (4)12―21
乘法：有理数乘法的法则：两数相乘，同号得正，异号得负，并把绝对值相乘；任何数同0相乘，都得0?
练习：
①(－5)×(－6)
②
乘法交换律： a b = b a
乘法结合律： (ab)c=a(bc)
不等于0的数相乘，积的符号由负因数的个数决定，当负因数有奇数个时，积为负；当负因数有偶数个时，积为正.
几个数相乘，有一个因数为0，积就为0.
乘法分配律：一个数同两个数的和相乘，等于把这个数分别同这两个数相乘，再把积相加。即a(b＋c)＝ab＋ac.
练习： ①4×(―12)+(―5)×(―8)+16；
②
除法：有理数除法则：除以一个数等于乘上这个数的倒数.
注意：0不能作除数.
两数相除，同号得正，异号得负，并把绝对值相除.
0除以任何一个不等于0的数，都得0.
练习：（1）；
(2) ；
(3) 。
乘方：
n个相同的因数a 相乘，即，记作。
计算：(1) ；
(2) ；
(3)
正数的任何次幂都是正数；
负数的奇次幂是负数，负数的偶次幂是正数。
有理数混合运算的运算顺序规定如下：
①先算乘方，再算乘除，最后算加减；
②同级运算，按照从左至右的顺序进行；
③如果有括号，就先算小括号里的，再算中括号里的，最后算大括号里的。
计算：
3＋50÷22×()－1
有理数及其运算训练
（1）
（2）
（3）
（1）
（2）
（3）
（4）
(1)――+；
(2)(+9)―(+10)+(―2)―(―8)+3。
(1)(―12)―(+8)+(―6)―(―5)；
(2)(+3.7)―(―2.1)―1.8+(―2.6)；
(3)(―16)+(+20)―(+10)―(―11)；
(4)
(1)
(2)
(1) (―)÷(―)；
(2) ；
(3)
二、无理数
定义：无限不循环小数叫做无理数，如π=3.1415926…，，－1.010010001…，都是无理数
练习：1、实数3.14，，，，，0.10110111011110…，π， 中，有（ ）个无理数？
A．2个 B．3个 C．4个 D．5个
2、下列说法中，正确的是（ ）
A．带根号的数是无理数 B．无理数都是开不尽方的数
C．无限小数都是无理数 D．无限不循环小数是无理数
3、下列命题中，正确的个数是（ ）
①两个有理数的和是有理数； ②两个无理数的和是无理数；
③两个无理数的积是无理数； ④无理数乘以有理数是无理数；
⑤无理数除以有理数是无理数； ⑥有理数除以无理数是无理数。
A．0个 B．2个 C．4个 D．6个
无理数的特征：(1)．圆周率及一些含有的数；
(2)．有一定的规律，但不循环的无限小数。
(3)．开不尽方的数 (注意:带根号的数不一定是无理数)
开方：
算术平方根：如果一个正数的平方等于，即那么这个正数就叫做的算术平方根，记作“”，读作“根号”。
平方根: 如果一个数的平方等于，即那么这个正数就叫做的平方根（也叫做二次方根）
平方根的性质：
　 1．一个正数有两个平方根，它们互为相反数．
　　2．0有一个平方根，它是0本身．
3．负数没有平方根．
4、重要公式：
练习：判断下列各数是否有平方根。若有，求出其平方根；若没有，请说明理由。
（1）169； （2）；（3）14；（4）7 ；（5）-16
（6）等于多少？
（7）已知，求的值。
（8）如果一个正数的平方根为2a-7和a+4，求这个正数。
无理数训练：
（1）3的算术平方根为 ，的平方根为 。
（2）如果的平方根为，则 。
（3）的算术平方根的倒数为 ，算术平方根的相反数为 ，
算术平方根的立方为 。
（4）平方根等于它本身的数是 ，算术平方根等于它本身的数是 。
（5） （6）
（7） （8）
（9）若，求的值。
（10）若互为相反数，求的值
（11）已知的整数部分为，小数部分为，求的值。