2012年中考复习专题四一元一次方程
图片预览




文档简介
专题四 一元一次方程
一、一元一次方程:只含有一个未知数,且未知数次数是一的整式方程叫一元一次方程。通常形式是kx+b=0(k,b为常数,且k≠0)。
★ 判断一个方程是否是一元一次方程要抓住三点:⑴方程是整式方程;⑵化简后方程中只含有一个未知数;⑶经整理后方程中未知数的次数是1.
例:1、下列各式中是一元一次方程的有( )
x-1=4x ②5(x-1)=0③-5x=+1④6=x+6⑤x-1=⑥5x-7=8(2x+3)
A.6个 B.5个 C.4个 D.3个
2、已知方程2+3x=5是一元一次方程,则m= .
二、等式的性质:
(1)等式两边同时加一个数或减一同一个数,等式两边相等。
如果a=b,那么a+c=b+c
如果a=b,那么a-c=b-c
(2)等式两边同时乘一个数或除以同一个数(0除外),等式两边相等。
如果a=b,那么ac=bc
如果a=b(c≠0),那么
补充:
(3)(对称性):如果a=b,那么b=a
(4)(传递性):如果a=b,b=c,那么a=c
(5)(可加性):如果a=b,c=d,那么a+c=b+d
例:1、下列运用等式的性质对等式进行的变形中,正确的是 ( )
三、解方程就是求出使方程中等号左右两边相等的未知数的值,这个值就是方程的解。
例:1、方程2m+x=1和3x-1=2x+1有相同的解,则m的值为( ).
A.0 B.1 C.-2 D.-
2、方程的解是( )
A. B. C. 1 D. -1
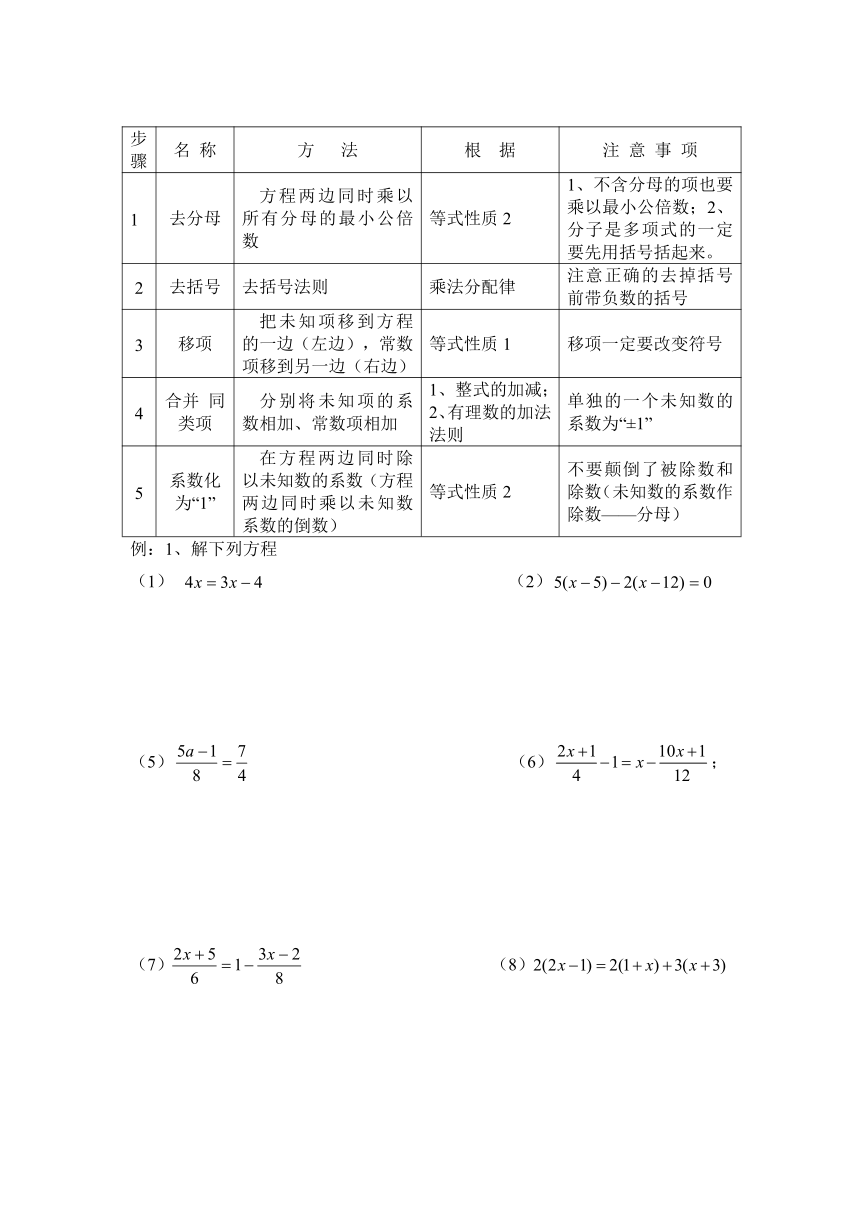
解一元一次方程有五个基本步骤:
步骤 名 称 方 法 根 据 注 意 事 项
1 去分母 方程两边同时乘以所有分母的最小公倍数 等式性质2 1、不含分母的项也要乘以最小公倍数;2、分子是多项式的一定要先用括号括起来。
2 去括号 去括号法则 乘法分配律 注意正确的去掉括号前带负数的括号
3 移项 把未知项移到方程的一边(左边),常数项移到另一边(右边) 等式性质1 移项一定要改变符号
4 合并 同类项 分别将未知项的系数相加、常数项相加 1、整式的加减;2、有理数的加法法则 单独的一个未知数的系数为“±1”
5 系数化为“1” 在方程两边同时除以未知数的系数(方程两边同时乘以未知数系数的倒数) 等式性质2 不要颠倒了被除数和除数(未知数的系数作除数——分母)
例:1、解下列方程
(1) (2)
(5) (6);
(7) (8)
2、当n为何值时关于x的方程的解为0?
四、实际问题与一元一次方程
1、列一元一次方程应用题的一般步骤:
审:审清题意,找出问题中的已知量和未知量;
设:用字母表示题目中的一个未知数;
列:根据所设的未知数找出等量关系列方程;
解:解方程,求未知数;
验:检验方程的解:一看单位是否统一;二看是否符合题意;
答:写出答案
2、实际问题的常见类型
销售问题
利润=售价—成本,
利润率=利润÷成本×100%
利润=成本×利润率
折扣:售价=商品标价×折扣
例:东方商场把进价为1890元的某商品按标价的8折出售,仍获利10%,则该商品的标价为多少?
(2).行程问题
路程=速度×时间
①相向问题:甲走的路程+乙走的路程=两地距离
追及问题:第一,同地不同时出发:前者走的路程=追者走的路程;
第二,同时不同地出发:前者走的路程+两地距离=追者所走的路程
③航行问题:
基本量、基本数量关系: 路程=速度×时间,
顺水速=静水速+水速, 逆水速=静水速-水速,
例:1、甲、乙两地相距162公里,一列慢车从甲站开出,每小时走48公里,一列快车从乙站开出,每小时走60公里试问:
两列火车同时相向而行,多少时间可以相遇?
两车同时反向而行,几小时后两车相距270公里?
若两车相向而行,慢车先开出1小时,再用多少时间两车才能相遇?
(4)若两车相向而行,快车先开25分钟,快车开了几小时与慢车相遇
3、一轮船航行于两个码头之间,逆水需10小时,顺水需6小时。已知水流速度为3千米/时,求该船在静水中的速度和两码头间的距离。
(3) 调配问题
劳动力调配问题:抓住从甲处人数与乙处人数间的关系来考虑
例:某车间22名工人生产螺钉和螺母,每人每天平均生产螺钉1200个或螺母2000个,一个螺钉要配两个螺母,为了使每天的产品刚好配套,应该分配多少名工人生产螺钉,多少工人生产螺母?
(4) 工程问题
基本量、基本数量关系:把总工作量看作单位“1”
工作量=工作效率×工作时间;
相等关系:各部分工作量之和等于1
例:要加工200个零件,甲先单独加工了5小时,然后又与乙一起加工4小时,完成了任务.已知甲每小时比乙多加工2个零件,求甲、乙每小时各加工多少个零件.
(5) 数字问题
两位数=十位数字×10+个位数字
例题7:一个两位数,十位上的数与个位上的数字之和为11,如果十位上的数字与个位上的数字对调,则所得的新数比原来大63,求原来两位数。
(6) 和差倍分问题(年龄问题)
基本相等关系:增长量=原有量×增长率,
现有量=原有量+增长量或现有量=原有量-降低量
例:小兵今年13岁,约翰的年龄的3倍比小兵的年龄的2倍多10岁,求约翰的年龄。
一元一次方程训练题:
1、下列各式中是一元一次方程的是( )
A. B.
C. D.
2、已知等式,则下列等式中不一定成立的是( )
(A) (B)
(C) (D)
3、方程的解是( )
(A) (B) (C) (D)
4、方程的解是,则等于( )
(A) (B) (C) (D)
5、解方程时,去分母后,正确结果是( )
A. B.
C. C.
6、电视机售价连续两次降价10%,降价后每台电视机的售价为a 元,则该电视机的原价为( )
A. 0.81a 元 B. 1.21a元 C. 元 D. 元
7、某商店卖出两件衣服,每件60元,其中一件赚25%,另一件亏25%,那么这两件衣服卖出后,商店是 ( )
A.不赚不亏 B.赚8元 C.亏8元 D. 赚8元
二、解方程:
1、 2、
3、 4、
5、 6、
7、 8、
三、已知是方程的根,
求代数式的值.
四、列方程解应用题
1、甲、乙骑自行车同时从相距65千米的两地相向而行,2小时相遇.甲比乙每小时多骑2.5千米,求甲乙的时速各是多少?
2.某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个。两个甲种部件和三个乙种部件配成一套,问加工甲乙部件各安排多少人才能使每天加工的甲、乙两种部件刚好配套?
3、一项工程,甲单独做20天完成,乙单独做10天完成,现在由乙先独做几天后,剩下的部分由甲独做,先后共花12天完成,问乙做了几天?
4、甲、乙两队完成某项工作,甲单独完成比乙单独完成快15天,如果甲单独先工作10天,再由乙单独工作15天,就可完成这项工作的,求甲、乙两人单独完成这项工作各需多少天?
5、一个两位数,十位数字与个位数字之和是13,如果把十位数字与个位数字对调得到的两位数比原数大45,求这个两位数.
6、有一个两位数,它的十位上的数字比个位上的数字大4,且这个两位数比构成它的两个数码之和的7倍还要大3,求这个两位数.
7、小华参加日语培训,为期8天,这8天的和为100,问小华几号结束培训?
8、三个连续偶数的和比其中最大的一个数大10,这三个连续偶数是什么?
9、有一块棱长为4厘米的正方体铜块,要将它熔化后铸成长2厘米、宽4厘米的长方体铜块,铸成后的铜块的高是多少厘米(不计损耗)?
10、将一罐满水的直径为40厘米,高为60厘米的圆柱形水桶里的水全部灌于另一半径为30厘米的圆柱形水桶里,问这时水的高度是多少?
一、一元一次方程:只含有一个未知数,且未知数次数是一的整式方程叫一元一次方程。通常形式是kx+b=0(k,b为常数,且k≠0)。
★ 判断一个方程是否是一元一次方程要抓住三点:⑴方程是整式方程;⑵化简后方程中只含有一个未知数;⑶经整理后方程中未知数的次数是1.
例:1、下列各式中是一元一次方程的有( )
x-1=4x ②5(x-1)=0③-5x=+1④6=x+6⑤x-1=⑥5x-7=8(2x+3)
A.6个 B.5个 C.4个 D.3个
2、已知方程2+3x=5是一元一次方程,则m= .
二、等式的性质:
(1)等式两边同时加一个数或减一同一个数,等式两边相等。
如果a=b,那么a+c=b+c
如果a=b,那么a-c=b-c
(2)等式两边同时乘一个数或除以同一个数(0除外),等式两边相等。
如果a=b,那么ac=bc
如果a=b(c≠0),那么
补充:
(3)(对称性):如果a=b,那么b=a
(4)(传递性):如果a=b,b=c,那么a=c
(5)(可加性):如果a=b,c=d,那么a+c=b+d
例:1、下列运用等式的性质对等式进行的变形中,正确的是 ( )
三、解方程就是求出使方程中等号左右两边相等的未知数的值,这个值就是方程的解。
例:1、方程2m+x=1和3x-1=2x+1有相同的解,则m的值为( ).
A.0 B.1 C.-2 D.-
2、方程的解是( )
A. B. C. 1 D. -1
解一元一次方程有五个基本步骤:
步骤 名 称 方 法 根 据 注 意 事 项
1 去分母 方程两边同时乘以所有分母的最小公倍数 等式性质2 1、不含分母的项也要乘以最小公倍数;2、分子是多项式的一定要先用括号括起来。
2 去括号 去括号法则 乘法分配律 注意正确的去掉括号前带负数的括号
3 移项 把未知项移到方程的一边(左边),常数项移到另一边(右边) 等式性质1 移项一定要改变符号
4 合并 同类项 分别将未知项的系数相加、常数项相加 1、整式的加减;2、有理数的加法法则 单独的一个未知数的系数为“±1”
5 系数化为“1” 在方程两边同时除以未知数的系数(方程两边同时乘以未知数系数的倒数) 等式性质2 不要颠倒了被除数和除数(未知数的系数作除数——分母)
例:1、解下列方程
(1) (2)
(5) (6);
(7) (8)
2、当n为何值时关于x的方程的解为0?
四、实际问题与一元一次方程
1、列一元一次方程应用题的一般步骤:
审:审清题意,找出问题中的已知量和未知量;
设:用字母表示题目中的一个未知数;
列:根据所设的未知数找出等量关系列方程;
解:解方程,求未知数;
验:检验方程的解:一看单位是否统一;二看是否符合题意;
答:写出答案
2、实际问题的常见类型
销售问题
利润=售价—成本,
利润率=利润÷成本×100%
利润=成本×利润率
折扣:售价=商品标价×折扣
例:东方商场把进价为1890元的某商品按标价的8折出售,仍获利10%,则该商品的标价为多少?
(2).行程问题
路程=速度×时间
①相向问题:甲走的路程+乙走的路程=两地距离
追及问题:第一,同地不同时出发:前者走的路程=追者走的路程;
第二,同时不同地出发:前者走的路程+两地距离=追者所走的路程
③航行问题:
基本量、基本数量关系: 路程=速度×时间,
顺水速=静水速+水速, 逆水速=静水速-水速,
例:1、甲、乙两地相距162公里,一列慢车从甲站开出,每小时走48公里,一列快车从乙站开出,每小时走60公里试问:
两列火车同时相向而行,多少时间可以相遇?
两车同时反向而行,几小时后两车相距270公里?
若两车相向而行,慢车先开出1小时,再用多少时间两车才能相遇?
(4)若两车相向而行,快车先开25分钟,快车开了几小时与慢车相遇
3、一轮船航行于两个码头之间,逆水需10小时,顺水需6小时。已知水流速度为3千米/时,求该船在静水中的速度和两码头间的距离。
(3) 调配问题
劳动力调配问题:抓住从甲处人数与乙处人数间的关系来考虑
例:某车间22名工人生产螺钉和螺母,每人每天平均生产螺钉1200个或螺母2000个,一个螺钉要配两个螺母,为了使每天的产品刚好配套,应该分配多少名工人生产螺钉,多少工人生产螺母?
(4) 工程问题
基本量、基本数量关系:把总工作量看作单位“1”
工作量=工作效率×工作时间;
相等关系:各部分工作量之和等于1
例:要加工200个零件,甲先单独加工了5小时,然后又与乙一起加工4小时,完成了任务.已知甲每小时比乙多加工2个零件,求甲、乙每小时各加工多少个零件.
(5) 数字问题
两位数=十位数字×10+个位数字
例题7:一个两位数,十位上的数与个位上的数字之和为11,如果十位上的数字与个位上的数字对调,则所得的新数比原来大63,求原来两位数。
(6) 和差倍分问题(年龄问题)
基本相等关系:增长量=原有量×增长率,
现有量=原有量+增长量或现有量=原有量-降低量
例:小兵今年13岁,约翰的年龄的3倍比小兵的年龄的2倍多10岁,求约翰的年龄。
一元一次方程训练题:
1、下列各式中是一元一次方程的是( )
A. B.
C. D.
2、已知等式,则下列等式中不一定成立的是( )
(A) (B)
(C) (D)
3、方程的解是( )
(A) (B) (C) (D)
4、方程的解是,则等于( )
(A) (B) (C) (D)
5、解方程时,去分母后,正确结果是( )
A. B.
C. C.
6、电视机售价连续两次降价10%,降价后每台电视机的售价为a 元,则该电视机的原价为( )
A. 0.81a 元 B. 1.21a元 C. 元 D. 元
7、某商店卖出两件衣服,每件60元,其中一件赚25%,另一件亏25%,那么这两件衣服卖出后,商店是 ( )
A.不赚不亏 B.赚8元 C.亏8元 D. 赚8元
二、解方程:
1、 2、
3、 4、
5、 6、
7、 8、
三、已知是方程的根,
求代数式的值.
四、列方程解应用题
1、甲、乙骑自行车同时从相距65千米的两地相向而行,2小时相遇.甲比乙每小时多骑2.5千米,求甲乙的时速各是多少?
2.某车间有技术工人85人,平均每天每人可加工甲种部件16个或乙种部件10个。两个甲种部件和三个乙种部件配成一套,问加工甲乙部件各安排多少人才能使每天加工的甲、乙两种部件刚好配套?
3、一项工程,甲单独做20天完成,乙单独做10天完成,现在由乙先独做几天后,剩下的部分由甲独做,先后共花12天完成,问乙做了几天?
4、甲、乙两队完成某项工作,甲单独完成比乙单独完成快15天,如果甲单独先工作10天,再由乙单独工作15天,就可完成这项工作的,求甲、乙两人单独完成这项工作各需多少天?
5、一个两位数,十位数字与个位数字之和是13,如果把十位数字与个位数字对调得到的两位数比原数大45,求这个两位数.
6、有一个两位数,它的十位上的数字比个位上的数字大4,且这个两位数比构成它的两个数码之和的7倍还要大3,求这个两位数.
7、小华参加日语培训,为期8天,这8天的和为100,问小华几号结束培训?
8、三个连续偶数的和比其中最大的一个数大10,这三个连续偶数是什么?
9、有一块棱长为4厘米的正方体铜块,要将它熔化后铸成长2厘米、宽4厘米的长方体铜块,铸成后的铜块的高是多少厘米(不计损耗)?
10、将一罐满水的直径为40厘米,高为60厘米的圆柱形水桶里的水全部灌于另一半径为30厘米的圆柱形水桶里,问这时水的高度是多少?
同课章节目录
