第8章平面图形的全等与相似复习学案

侨 润 中 学 教 学 案 八 年级 数学学科
第 5 周 第 1 节 总 21 课时 主备人 唐云玲 授课人 上课时间 2012 年 3月 12日
课题 第8章平面图形的全等和相似 课型 复习题
教学目标 理解全等和相似的概念，能识别全等和相似中的对应元素。掌握全等和相似的性质与判定方法。能运用全等和相似的判定和性质进行简单证明。了解全等和相似多边形的概念和性质
重点 掌握全等和相似的性质与判定方法 难点 能运用全等和相似的判定和性质进行简单证明
激情导入
教 学 过 程 教学措施
一．知识要点：1. 叫做全等形，全等形的形状 ，大小 ；2. 叫做相似形，相似形的形状 ，大小 。3. 叫做全等三角形。4.全等三角形的性质：全等三角形的对应边 ，对应角 。5全等三角形的判定方法有：（1）ASA （又叫做 ）：用自然语言叙述为 ；例如在图1中，应满足 、 、 能用ASA推出△ABC≌△DEF；（2）AAS （又叫做 ）：用自然语言叙述为 ；例如在图1中，应满足 、 、 能用ASA推出△ABC≌△DEF；（3）SAS （又叫做 ）：用自然语言叙述为 ；例如在图1中，应满足 、 、 能用ASA推出△ABC≌△DEF；（4）SSS （又叫做 ）：用自然语言叙述为 ；例如在图1中，应满足 、 、 就能用ASA推出△ABC≌△DEF；
教 学 过 程 教学措施
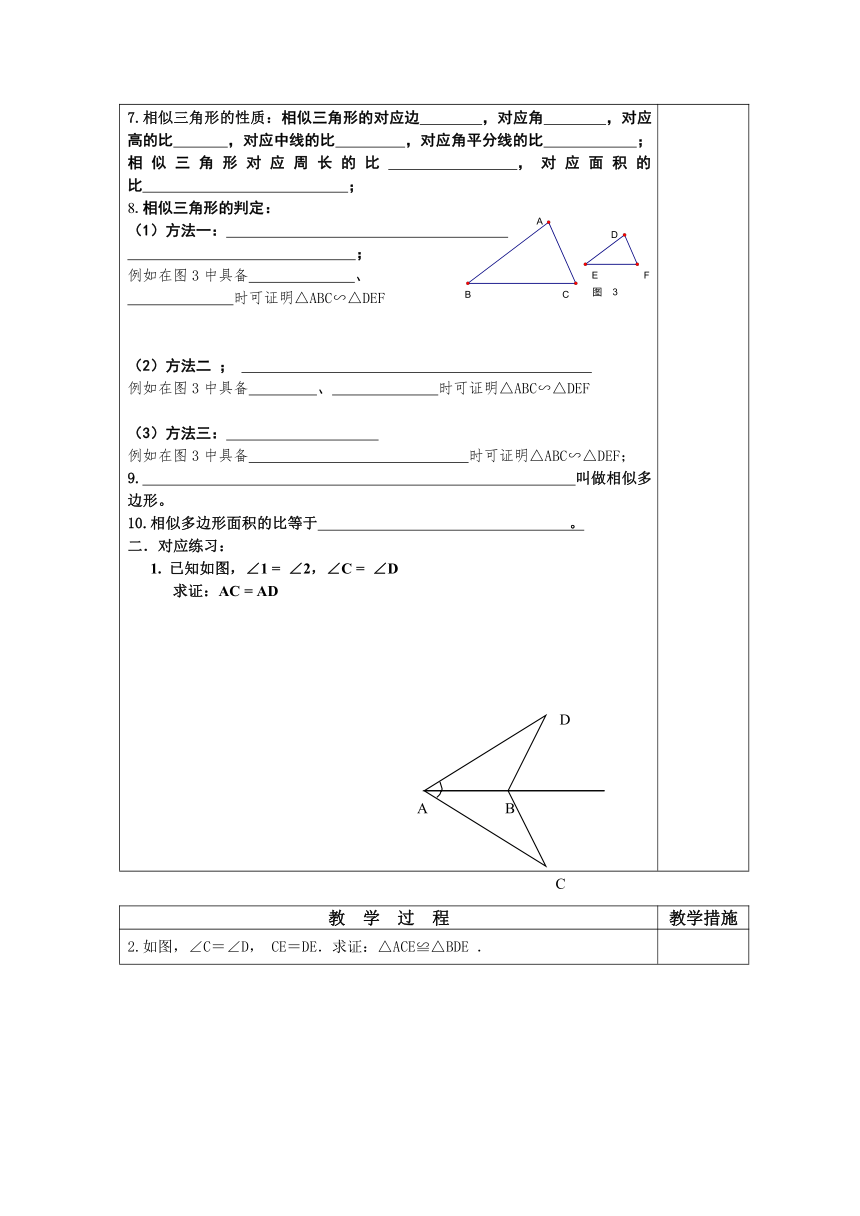
6. 叫做相似三角形；全等三角形与相似三角形的关系 。7.相似三角形的性质：相似三角形的对应边 ，对应角 ，对应高的比 ，对应中线的比 ，对应角平分线的比 ；相似三角形对应周长的比 ，对应面积的比 ；8.相似三角形的判定： （1）方法一： ；例如在图3中具备 、 时可证明△ABC∽△DEF（2）方法二 ； 例如在图3中具备 、 时可证明△ABC∽△DEF（3）方法三： 例如在图3中具备 时可证明△ABC∽△DEF；9. 叫做相似多边形。10.相似多边形面积的比等于 。二．对应练习： 1. 已知如图，∠1 = ∠2，∠C = ∠D 求证：AC = AD
教 学 过 程 教学措施
2.如图，∠C＝∠D， CE＝DE．求证：△ACE≌△BDE ．3.已知如图,AE＝AC,AB＝AD,∠EAB＝∠CAD,试说明:∠B＝∠D4、如图，E、C在BF上，AB=DE，AC=DF，BE=CF，求证：∠A=∠D。 A D B E C F
教 学 过 程 教学措施
5.依据下列各组条件,判定△ABC与△DEF是否相似,并说明为什么：⑴ ∠A=120°, AB=7cm, AC=14cm, ∠D=120°, DE=3cm, DF=6cm.（2）AB=4cm, BC=6cm, AC=8cm, DE=12cm , EF=18cm, DF=24cm6.如图:试说明△ADC∽△ACB △ADC∽△CDB
感悟反思
A
B
D
C
A
D
B
C