全等三角形综合练习(无答案)
文档属性
| 名称 | 全等三角形综合练习(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 64.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-15 00:00:00 | ||
图片预览


文档简介
三角形全等典型例题分析
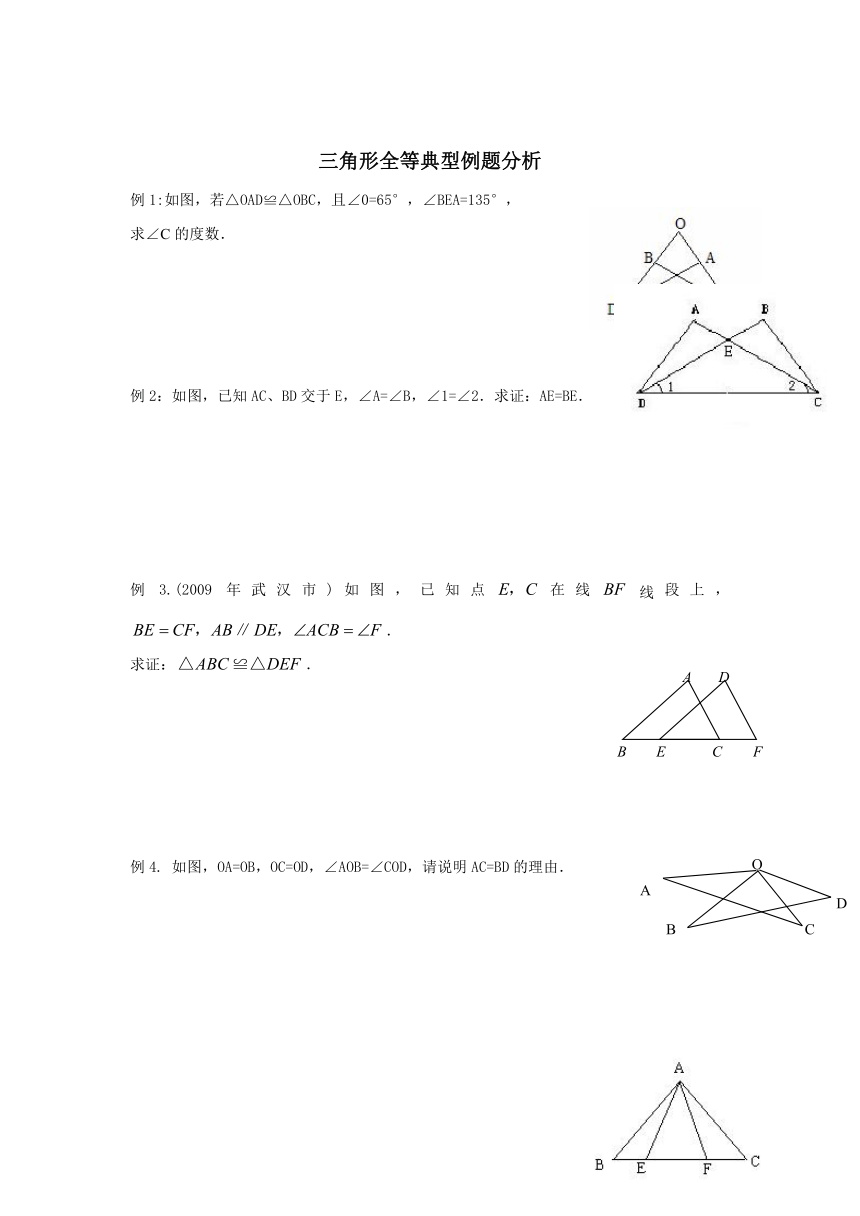
例1:如图,若△OAD≌△OBC,且∠0=65°,∠BEA=135°,
求∠C的度数.
例2:如图,已知AC、BD交于E,∠A=∠B,∠1=∠2.求证:AE=BE.
例3.(2009年武汉市)如图,已知点在线线段上,.
求证:.
例4. 如图,OA=OB,OC=OD,∠AOB=∠COD,请说明AC=BD的理由.
例5.如图,AE=AF,∠AEF=∠AFE,BE=CF,说明AB=AC。
例6.如图,是一个风筝模型的框架,由DE=DF,EH=FH,就说明∠DEH=∠DFH。试用你所学的知识说明理由。
例7. 如图,已知∠B=∠E=90°,AC=DF,BF=EC.求证:AB=DE.
例8.(2009年浙江省)已知命题:如图,点A,D,B,E在同一条直线上,且AD=BE,∠A=∠FDE,则△ABC≌△DEF.判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一个适当条件 使它成为真命题,并加以证明.
例9:如图所示,已知AD为等腰三角形ABC的底角的平分线,∠C=90°,求证:AB=AC+CD.
巩固练习
1.△ABC≌△DEF,且△ABC的周长为12,若AB=3,EF=4,则AC= .
2.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带去 块.
3. 如图所示,等腰直角三角形ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,若AB=15,则△BDE的周长为 。
4. (2011广东湛江19,4分)如图,点在同一直线上, ,,
(填“是”或“不是”) 的对顶角,要使,还需添加一个条件,这个条件可以是 (只需写出一个).
5.把下列说明Rt△ABC≌Rt△DEF的条件或根据补充完整.
(1) _______,∠A=∠D ( ASA )
(2) AC=DF,________ (SAS)
(3) AB=DE,BC=EF ( )
(4) AC=DF, ______ ( HL )
(5) ∠A=∠D, BC=EF ( )
(6) ________,AC=DF ( AAS )
6. (2011上海,5,4分)下列命题中,真命题是( ).
(A)周长相等的锐角三角形都全等; (B) 周长相等的直角三角形都全等
(C)周长相等的钝角三角形都全等; (D) 周长相等的等腰直角三角形都全等
7. (2011江苏宿迁,7,3分)如图,已知∠1=∠2,
则不一定能使△ABD≌△ACD的条件是( )
A.AB=AC B.BD=CD
C.∠B=∠C D.∠ BDA=∠CDA
8.如图,AB平分∠CAD,E为AB上一点,若AC=AD,则下列结论错误的是( )
A、BC=BD; B、CE=DE;
C、BA平分∠CBD; D、图中有两对全等三角
9.如图,已知AB=AC,BD=DC,那么下列结论中不正确的是( )
A.△ABD≌△ACD B.∠ADB=90°
C.∠BAD是∠B的一半 D.AD平分∠BAC
10.(8分)已知:如图,A、C、F、D在同一直线上,AF=DC,AB=DE,BC=EF,
求证:△ABC≌△DEF.
11. (2011山东菏泽,15(2),6分)已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.求证:AB=DC
12.(8分)如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是28,AB=20cm,AC=8cm,求DE的长.
C
E
B
F
D
A
B
A
O
C
D
A
B
C
E
D
(第3题图)
(第2题图)
B
C
D
E
F
A
A
E
B
D
C
F
例1:如图,若△OAD≌△OBC,且∠0=65°,∠BEA=135°,
求∠C的度数.
例2:如图,已知AC、BD交于E,∠A=∠B,∠1=∠2.求证:AE=BE.
例3.(2009年武汉市)如图,已知点在线线段上,.
求证:.
例4. 如图,OA=OB,OC=OD,∠AOB=∠COD,请说明AC=BD的理由.
例5.如图,AE=AF,∠AEF=∠AFE,BE=CF,说明AB=AC。
例6.如图,是一个风筝模型的框架,由DE=DF,EH=FH,就说明∠DEH=∠DFH。试用你所学的知识说明理由。
例7. 如图,已知∠B=∠E=90°,AC=DF,BF=EC.求证:AB=DE.
例8.(2009年浙江省)已知命题:如图,点A,D,B,E在同一条直线上,且AD=BE,∠A=∠FDE,则△ABC≌△DEF.判断这个命题是真命题还是假命题,如果是真命题,请给出证明;如果是假命题,请添加一个适当条件 使它成为真命题,并加以证明.
例9:如图所示,已知AD为等腰三角形ABC的底角的平分线,∠C=90°,求证:AB=AC+CD.
巩固练习
1.△ABC≌△DEF,且△ABC的周长为12,若AB=3,EF=4,则AC= .
2.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是带去 块.
3. 如图所示,等腰直角三角形ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,若AB=15,则△BDE的周长为 。
4. (2011广东湛江19,4分)如图,点在同一直线上, ,,
(填“是”或“不是”) 的对顶角,要使,还需添加一个条件,这个条件可以是 (只需写出一个).
5.把下列说明Rt△ABC≌Rt△DEF的条件或根据补充完整.
(1) _______,∠A=∠D ( ASA )
(2) AC=DF,________ (SAS)
(3) AB=DE,BC=EF ( )
(4) AC=DF, ______ ( HL )
(5) ∠A=∠D, BC=EF ( )
(6) ________,AC=DF ( AAS )
6. (2011上海,5,4分)下列命题中,真命题是( ).
(A)周长相等的锐角三角形都全等; (B) 周长相等的直角三角形都全等
(C)周长相等的钝角三角形都全等; (D) 周长相等的等腰直角三角形都全等
7. (2011江苏宿迁,7,3分)如图,已知∠1=∠2,
则不一定能使△ABD≌△ACD的条件是( )
A.AB=AC B.BD=CD
C.∠B=∠C D.∠ BDA=∠CDA
8.如图,AB平分∠CAD,E为AB上一点,若AC=AD,则下列结论错误的是( )
A、BC=BD; B、CE=DE;
C、BA平分∠CBD; D、图中有两对全等三角
9.如图,已知AB=AC,BD=DC,那么下列结论中不正确的是( )
A.△ABD≌△ACD B.∠ADB=90°
C.∠BAD是∠B的一半 D.AD平分∠BAC
10.(8分)已知:如图,A、C、F、D在同一直线上,AF=DC,AB=DE,BC=EF,
求证:△ABC≌△DEF.
11. (2011山东菏泽,15(2),6分)已知:如图,∠ABC=∠DCB,BD、CA分别是∠ABC、∠DCB的平分线.求证:AB=DC
12.(8分)如图,在△ABC中,AD为∠BAC的平分线,DE⊥AB于E,DF⊥AC于F,△ABC面积是28,AB=20cm,AC=8cm,求DE的长.
C
E
B
F
D
A
B
A
O
C
D
A
B
C
E
D
(第3题图)
(第2题图)
B
C
D
E
F
A
A
E
B
D
C
F
