1.6函数y=Asin(x+φ)的性质与图象-【新教材】2020-2021学年北师大版(2019)高中数学必修第二册课件(74张PPT)
文档属性
| 名称 | 1.6函数y=Asin(x+φ)的性质与图象-【新教材】2020-2021学年北师大版(2019)高中数学必修第二册课件(74张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 00:00:00 | ||
图片预览









文档简介
函数y=Asin(????????+ φ )
的性质与图象
?
授课教师:
温故知新
学习目标
1. 了解匀速圆周运动的数学模型.
2. 理解A,????, φ对函数图象变化的影响,并掌握由y=sinx的图象得到y=Asin(????????+φ)的图象.(难点)
3. 知道函数y=Asin(????????+φ)中常数A,????, φ的物理意义,理解振幅、相位、初相的概念.(重点)
?
课文精讲
问题提出
“南昌之星”摩天轮于2006年竣工,总高度160 m,直径153 m匀速旋转一圈需时30 min.
以摩天轮的中心为原点建立平面直角坐标系,画示意图,如图.
课文精讲
设座舱A为起始位置如图,OA与x轴所形成的角为?????????,因为转一圈需要30 min,所以每分所转的角度为 .
经过x min后,OA旋转到OA′, OA′与x轴所形成角的大小为 .
?
?????????????????????????
?
????????????????=????????????
?
课文精讲
因为直径为153 m,总高度为160 m,所以OA的长为76.5 m,轮子的最低点与地面距离为160-153=7(m),原点O距离地面的距离为7+76.5=83.5(m).从而点A′到地面的距离y与时间x的关系为
y =76.5sin ??????????????????????????+83.5.
?
课文精讲
在物理和工程技术中会遇到一些问题,其中的函数关系都是形如y=Asin(????x+φ)(其中A,????,φ是常数,A>0,????>0)的形式.这类函数有什么性质呢?
从解析式来看,若A=1,????=1, φ =0,函数y=Asin(????x+φ)就是y=sinx.下面,我们就来探究A,????,φ的取值对y=Asin(????x+φ)的图象的影响.
?
课文精讲
实例分析
考虑这类函数的一个特例:y=sin2x,x∈R.
1.周期
由sin2x=sin(2x+2π)= sin 2(x+π),根据周期函数的定义,y=sin2x是周期函数,π是y=
sin2x的最小正周期.
探究????对y=sin????????的图象的影响
?
课文精讲
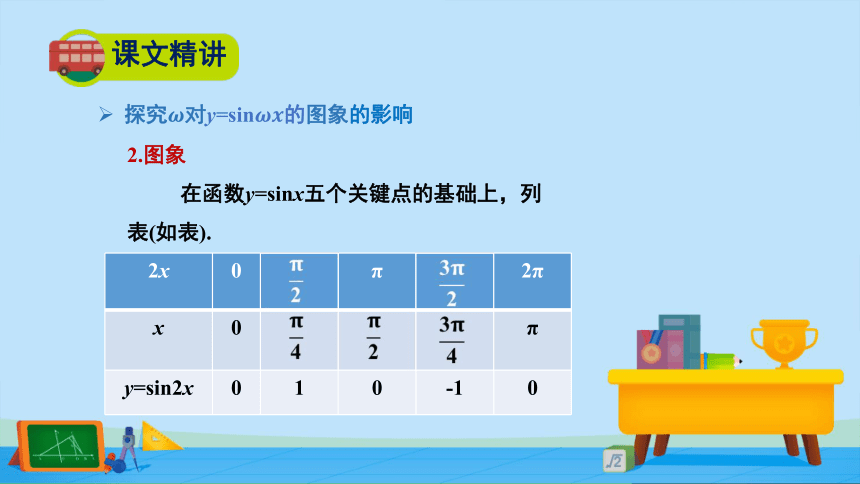
2.图象
在函数y=sinx五个关键点的基础上,列表(如表).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}2x
0
π
2π
x
0
π
y=sin2x
0
1
0
-1
0
探究????对y=sin????????的图象的影响
?
课文精讲
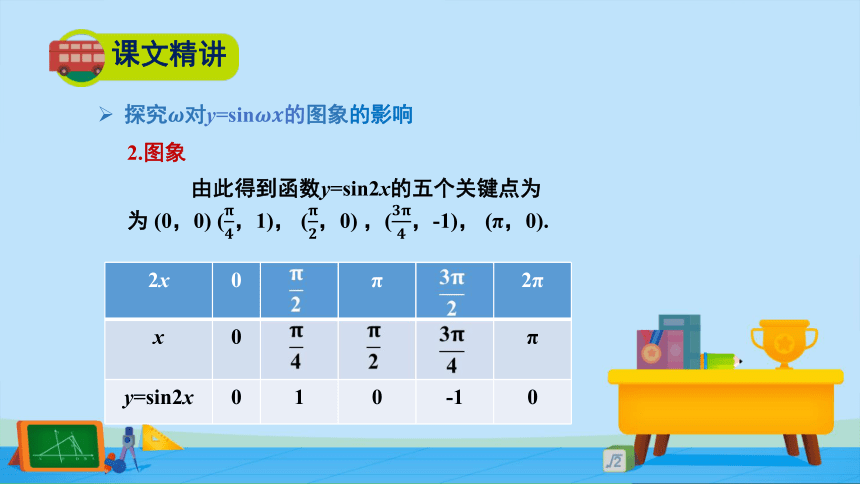
2.图象
由此得到函数y=sin2x的五个关键点为为 (0,0) (????????,1), (????????,0) ,(????????????,-1), (π,0).
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}2x
0
π
2π
x
0
π
y=sin2x
0
1
0
-1
0
探究????对y=sin????????的图象的影响
?
课文精讲
2.图象
画出该函数在一个周期[0,π]上的图象.由函数y=sin2x的周期性,把图象向左、右延拓,得到y=sin2x在R上的图象(如图).
探究????对y=sin????????的图象的影响
?
课文精讲
2.图象
从函数y=sin2x的图象看出,将函数y=sin x图象上每个点的横坐标都缩短为原来的????????,纵坐标不变,就得到函数y=sin2x的图象(如图),且最小正周期变为π.
?
探究????对y=sin????????的图象的影响
?
课文精讲
3.单调性
从图象上可以看出,函数y=sin2x在区间[kπ ?????????, kπ+ ????????],k∈Z 上单调递增;在区间
[kπ +????????, kπ+ ????????????],k∈Z上单调递减.
?
探究????对y=sin????????的图象的影响
?
课文精讲
4.最大(小)值和值域
在区间[0,π]上,当x=????????时,函数y=sin2x,取得最大值1;当x=????????????时,函数y=sin2x取得最小值-1.由函数y=sin2x的周期性可知,当x=kπ+????????,k∈Z时,它取得最大值1;当x=kπ+????????????,k∈Z时,它取得最小值-1.
?
探究????对y=sin????????的图象的影响
?
课文精讲
4.最大(小)值和值域
函数y=sin2x 的图象夹在两条平行线y=1和y=?1之间,所以它的值域是[-1,1].
?
探究????对y=sin????????的图象的影响
?
典型例题
例1:求函数y=sin????????x的周期,并画出其图象.
?
解:由y=sinx的周期性可知, y=sin????????x=
sin????????????+?????????=sin????????(x+ 6????) .根据周期函数
的定义, y=sin????????x是周期函数, 6????是它的
最小正周期.
?
典型例题
例1:求函数y=sin????????x的周期,并画出其图象.
?
解:在函数y=sinx五个关键点的基础上,列
表(如表).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
0
π
2π
x
0
6π
0
1
0
-1
0
典型例题
例1:求函数y=sin????????x的周期,并画出其图象.
?
解:于是得到函数y=sin????????x在区间上的五个关
键点为 (0,0) (?????????????,1), (3π,0) ,(????????????,
-1), (6π,0).
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
0
π
2π
x
0
6π
0
1
0
-1
0
典型例题
例1:求函数y=sin????????x的周期,并画出其图象.
?
解:画出该函数在一个周期[0,6π]上的图象.
由函数y=sin????????x的周期性,把图象向左、
右延拓,得到y=sin????????x 在R上的图象(如图).
?
典型例题
例1:求函数y=sin????????x的周期,并画出其图象.
?
解:从函数y=sin????????x的图象看出,对同一个x值,
将函数y=sinx图象上每个点的横坐标都伸
长到原来的3倍,纵坐标不变,就得到函
数y=sin????????x的图象(如图).
?
课文精讲
一般地,对于????>0,有
sin????x= sin(????x +2π)= sin????????+????????????.
根据周期函数的定义,T=????????????是函数y=sin????x的最小正周期·
?
探究????对y=sin????????的图象的影响
?
课文精讲
函数y=sin????x的图象是将函数y=sinx图象上所有点的横坐标缩短到原来的?????????(当????>1时)或伸长(当0?
探究????对y=sin????????的图象的影响
?
课文精讲
sin(x +φ)的图象
横坐标伸长(0<????<1)或缩短到(????>1)原来的????????倍,纵坐标不变
?
sin(????????+φ)的图象
?
探究????对y=sin????????的图象的影响
?
课文精讲
①????的作用:引起周期T=????????????的改变,这种变换叫
横向伸缩.
?
③函数y=Asin(????x+φ)(????>0,≠1)的图象横向伸
长,周期变大,x的系数变小;横向缩短,周
期变小,x的系数变大.
?
② y=Asin(x+φ)的图象与y=Asin(????x+φ)的图象形
状不同.
?
探究????对y=sin????????的图象的影响
?
课文精讲
考虑这类函数的一个特例: y=sin?????????????.
我们已经知道,函数y=sin?????????????的图象是由函数y=sin????的图象平移得到的.令?????????????=0,得????=????????,即函数y=sin????图象上的点(????,0)向右平移到点(????????,0),所以函数 y=sin?????????????的图象是将函数y=sin????图象上的所有点向右平移????????个单位长度得到的.
?
探究????对y=sin????????的图象的影响
?
课文精讲
从而将刻画函数y=sinx基本形状的五个关键点 (0,0) (????????,1), (π,0) ,(????????????,-1), (2π,0)向右平移??????????个单位长度,得到刻画函数y=sin?????????????基本形状的五个关键点为点 (????????,0),(????????????,1), (????????????,0) ,(????????????????,-1), (????????????,0).
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
画出该函数在一个周期[????????,?????????????]上的图象.由函数y=sin?????????????的周期性,把图延拓到R,得到该函数在R上的图象(如图).
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
从图象上可以看出,函数y=sin??????????????在区间[2kπ?????????, 2kπ+ ????????????],k∈Z上都单调递增;在区间[2kπ+????????????, 2kπ+ ?????????????????],k∈Z上都单调递减.
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
当x=2kπ+????????????,k∈Z时,它取得最大值1;当x=2kπ+ ???????????????? ,k∈Z时,它取得最小值-1.
函数y=sin?????????????的图象夹在两条平行线y=1和y=-1之间,所以它的值域是[-1,1].
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
思考
怎样通过平移函数y=sinx的图象得到y=sin????+?????????的图象?
?
函数y=sinx上的所有点向左平移????????个单位长度得到y=sin????+?????????的图象.
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
概括
函数y=sin(x+φ)与函数y=sinx的周期相同,由x+φ=0,得x=?φ,即函数y=sinx图象上的点(0,0)平移到了点(-φ,0).
函数y=sin(x+φ)的图象,可以看作将函数y=sinx图象上的所有点向左(φ>0)或向右(φ<0)平移|φ|个单位长度得到的.
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
下面来研究函数y=sin????????+??????????的性质.
?
1.周期
y=sin????????+??????????=sin????????+????????+????????=sin[????????+????+????????]
根据周期函数的定义, y=sin????????+??????????是周期函数,π是它的最小正周期. 即函数, y=sin????????+??????????与函数y=sin2x周期相同·
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
2.图象
通过表确定五个关键点.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
0
π
2π
x
0
1
0
-1
0
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
2.图象
由此得到在区间[??????????????, ?????????????????????]上刻画该函数基本形状的五个关键点为??????????????,????,??????????,????, ?????????????????,????, ????????????,?????, ????????????????????,????.
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
2.图象
画出函数y=sin????????+??????????在区间[??????????????, ?????????????????????]上的图象.由函数y=sin????????+??????????的周期性,把图象向左、右延拓,就可得到它在R上的图象(如图).
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
2.图象
它也可以由函数y=sin2x的图象向左平移?????????????得到·
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
3.单调性
从图可以看出,函数y=sin????????+??????????在区间[kπ ?????????, kπ+??????????],k∈Z 上单调递增;在区间
[kπ+??????????, kπ+ ????????????],k∈Z上单调递减.
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
4.最大(小)值和值域
当x=kπ+ ?????????,k∈Z时, 函数y=sin????????+??????????取得最大值1;当x=kπ+????????????,k∈Z时,它取得最小值-1.
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
4.最大(小)值和值域
函数y=sin??????????????????的图象夹在两条平行线y=1和y=?1之间,所以它的值域是[-1,1].
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
概括
函数y=sin(????x +φ)与函数y=sin????x有相同的周期,由????x +φ =0,得x=?????????,即函数y=sin????x 图象上的点(0,0)平移到点(??????????,0).函数y=sin(????x +φ)的图象,可以看作将函数y=sin????x图象上的所有点向左(φ>0)向右(φ<0)平移|????????|个单位长度得到的.
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
概括
在函数y=sin(????x +φ)中, φ决定了x=0时的函数值,通常称φ为初相,????x +φ为相位.
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
概括
①φ的变化引起图象位置的变化.
② y=sin(x+φ)的图象与y=sinx的图象形状完全
一样,且由y=sinx的图象向左(右)平移得到;
y=sinx的图象
探究????对y=sin(x+φ)的图象的影响
?
向左(φ>0)或向右(φ<0)平移| φ |个单位长度
y=sin(x+φ)的图象
课文精讲
谢 谢
课文精讲
探究????对y=Asin(????x+φ)的图象的影响
?
探究函数y=2sin????????+????????的周期,并画出它的图象.
?
函数y=2sin????????+?????????与函数y=sin????????+?????????有相同的周期,即它的周期是π.
?
课文精讲
前面已经画出了函数y=2sin????????+?????????的图象,并讨论了它的性质,所以从解析表达式上容易得到,对于同一个x值,函数y=2sin????????+?????????图象上点的纵坐标等于函数y=sin????????+?????????图象上点的纵坐标的2倍.
?
探究????对y=Asin(????x+φ)的图象的影响
?
课文精讲
这表明,函数y=2sin????????+????????的图象,可以看作是将函数y=sin????????+????????图象上所有点的纵坐标伸长到原来的2倍(横坐标不变)而得到的.
?
探究????对y=Asin(????x+φ)的图象的影响
?
课文精讲
如图.
探究????对y=Asin(????x+φ)的图象的影响
?
课文精讲
概括
y=Asin(????x +φ)(A>0)的图象是将y=sin(????x +φ)的图象上的每个点的纵坐标伸长(当A>1时)
或缩短(当0?
探究????对y=Asin(????x+φ)的图象的影响
?
课文精讲
如何更好的理解呢?
①若A>0,则函数y=Asin(????x +φ)的值域为 [-A ,A],最大值为A,最小值为-A.
若A <0,则函数y=Asin(????x +φ)的值域为
[A ,-A] ,最大值为-A,最小值为A.
?
探究????对y=Asin(????x+φ)的图象的影响
?
②A的作用:引起值域的改变,这种变换叫
纵向伸缩.
课文精讲
如何更好的理解呢?
③|A|的大小反映了曲线y=Asin(????x +φ)的波
动幅度的大小.
?
探究????对y=Asin(????x+φ)的图象的影响
?
④y=Asin(????x +φ)与y=sin(????x +φ)的图象形状
不同.
?
课文精讲
思考
函数y=2sin????????+?????????+1与函数y=sin????????+?????????的图象有什么不同?
?
探究????对y=Asin(????x+φ)的图象的影响
?
课文精讲
综上关于????,φ,A这三个参数的讨论,可知探究函数y=Asin(????x+φ)(A>0,????>0,x∈R)性质的一般步骤:
第1步,确定周期T=????????????;
第2步,在y=sinx五个关键点(0,0),????????,????,
(????,????), ????????????,?????, ????????,???? 的基础上确定该函数的五个关键点;
?
探究????对y=Asin(????x+φ)的图象的影响
?
课文精讲
综上关于????,φ ,A这三个参数的讨论,可知探究函数y=Asin(????x+φ)(A>0,????>0,x∈R)性质的一般步骤:
第3步,用光滑曲线顺次连接五个关键点,即可画出函数y=Asin(????x+φ)(在一个周期上的图象,再利用其周期性把图象延拓到R,就可以得到它在R上的图象;
?
探究????对y=Asin(????x+φ)的图象的影响
?
课文精讲
综上关于????,φ ,A这三个参数的讨论,可知探究函数y=Asin(????x+φ)(A>0,????>0,x∈R)性质的一般步骤:
第4步,借助图象讨论性质.
实际上,这也是讨论周期函数的一般方法和步骤.
?
探究????对y=Asin(????x+φ)的图象的影响
?
课文精讲
步骤1
由y=sinx的图象得到y=Asin(????????+ φ ) (A>0,????>0)的图象的两种方法:
?
画出y=sinx的图象
得到y=sin(????+φ )的图象
?
得到y=sin(????????+ φ )的图象
?
得到y=Asin(????????+φ)的图象
?
向左(右)平移
| φ |个单位长度
步骤2
步骤3
步骤4
横坐标变为原来的????????倍
?
纵坐标变为原来的????倍
?
探究????对y=Asin(????x+φ)的图象的影响
?
课文精讲
由y=sinx的图象得到y=Asin(????????+ φ ) (A>0,????>0)的图象的两种方法:
?
步骤1
画出y=sinx的图象
得到y=sin????????的图象
?
得到y=sin(????????+ φ )的图象
?
得到y=Asin(????????+ φ)的图象
?
向左(右)平移|????|????个单位长度
?
步骤2
步骤3
步骤4
横坐标变为原来的????????倍
?
纵坐标变为原来的????倍
?
探究????对y=Asin(????x+φ)的图象的影响
?
典型例题
例2:画出函数y=cos????????????的图象,并讨论其基本性质.
?
解:方法一:
直接运用y=Asin(????x+φ)的结果,先变形,
y=cos????????????=sin??????????????????????=sin?????????????+????????,
再用上面的一般方法来研究.
?
典型例题
例2:画出函数y=cos????????????的图象,并讨论其基本性质.
?
解:方法二:使用类似y=Asin(????x+φ)的研究方法
(1)周期
因为y=cos????的周期是2π,所以cos????????????=
cos????????????+????????= cos???????? (x+4π),该函数的周期
为T=4π.
?
典型例题
例2:画出函数y=cos????????????的图象,并讨论其基本性质.
?
解:方法二:使用类似y=Asin(????x+φ)的研究方法
(2)图象
刻画函数y=cos????在区间[0,2π]上图象基
本形状的五个关键点为(0,1),????????,????,
(????,?????), ????????????,????, ????????,????.
?
典型例题
例2:画出函数y=cos????????????的图象,并讨论其基本性质.
?
解:方法二:使用类似y=Asin(????x+φ)的研究方法
(2)图象
由此得到刻画函数y=cos????????????在区间[0,
4π]上图象基本形状的五个关键点为(0,1),
?????????(????,????) , (????????,?????), ????????,????,
????????,????.
?
典型例题
例2:画出函数y=cos????????????的图象,并讨论其基本性质.
?
解:方法二:使用类似y=Asin(????x+φ)的研究方法
(2)图象
用光滑曲线顺次连接五个关键点画出函
数y=cos????????????在区间[0,4π]上的图象.由它的周
期性,把图象向左、右延拓,就可以得到它
在R上的图象(如图).
?
典型例题
例2:画出函数y=cos????????????的图象,并讨论其基本性质.
?
解:方法二:使用类似y=Asin(????x+φ)的研究方法
(2)图象
?
典型例题
例2:画出函数y=cos????????????的图象,并讨论其基本性质.
?
解:方法二:使用类似y=Asin(????x+φ)的研究方法
(3)其他性质
设????=????????????,则函数y=cosu的单调递增
区间[2kπ-π,2kπ],k∈Z.
由2kπ-π≤ ???????????? ≤ 2kπ,k∈Z,得4kπ-2π
≤ ????≤???????????? , k∈Z.
?
典型例题
例2:画出函数y=cos????????????的图象,并讨论其基本性质.
?
解:方法二:使用类似y=Asin(????x+φ)的研究方法
(3)其他性质
?
所以函数y=cos????????????的单调递增区间是[4kπ-2π,4kπ],k∈Z.
类似地,函数y=cos????????????的单调递减区间是[4kπ,4kπ+2π],k∈Z.
?
典型例题
例2:画出函数y=cos????????????的图象,并讨论其基本性质.
?
解:方法二:使用类似y=Asin(????x+φ)的研究方法
(3)其他性质
?
函数y=cosu,u∈R取得最大值的u的集合是{u| u= 2kπ,k∈Z}.
典型例题
例2:画出函数y=cos????????????的图象,并讨论其基本性质.
?
解:方法二:使用类似y=Asin(????x+φ)的研究方法
(3)其他性质
?
由?????????????= 2kπ ,得x= 4kπ,k∈Z,所以当x∈{x|x= 4kπ,k∈Z}时,函数y=cos????????????, x∈R取得最大值1.
?
典型例题
例2:画出函数y=cos????????????的图象,并讨论其基本性质.
?
解:方法二:使用类似y=Asin(????x+φ)的研究方法
(3)其他性质
?
类似地,当x∈{x|x= 4kπ+ 2π,k∈Z}时,函数y=cos????????????, x∈R取得最小值-1.
?
函数y=cos?????????????, x∈R的值域为[-1,1].
?
综合练习
若函数y=sin(2x + ????????) ,则它的最小正周期T=______.
?
解:T=????????????=????.
?
????
?
综合练习
已知函数f(x)=2sin(2x + ????????).
(1)求函数在[0,π]的单调递增区间;
(2)关于x的不等式f(x)<1的解集.
?
解: (1)令2kπ- ?????????≤2x + ????????≤2kπ+ ????????,
解得kπ- ?????????????????≤x≤kπ+????????????, k∈Z,
故 f(x)的单调递增区间[kπ- ?????????????????, kπ+????????????],
?
综合练习
已知函数f(x)=2sin(2x + ????????).
(1)求函数在[0,π]的单调递增区间;
(2)关于x的不等式f(x)<1的解集.
?
解:(1) 令k=0,单调递增区间为[-????????????????,????????????] ,
令k=1,单调递增区间为[????????????????,????????????????????],
故f(x)在[0,π]上的单调递增区间为[????,????????????] ∪[????????????????,????].
?
综合练习
已知函数f(x)=2sin(2x + ????????).
(1)求函数在[0,π]的单调递增区间;
(2)关于x的不等式f(x)<1的解集.
?
解: (2) 由f(x)=2sin(2x + ????????)<1得:
sin(2x + ????????)<????????,
故2kπ+ ?????????????<2x + ????????≤2kπ+ ????????????????,k∈Z,
解得:kπ+ ?????????<x≤kπ+ ????????????????????,k∈Z,
?
综合练习
已知函数f(x)=2sin(2x + ????????).
(1)求函数在[0,π]的单调递增区间;
(2)关于x的不等式f(x)<1的解集.
?
解: (2)所以f(x)<1的解集为:
(kπ+ ?????????, kπ+ ????????????????????).
?
本课小结
再 见
的性质与图象
?
授课教师:
温故知新
学习目标
1. 了解匀速圆周运动的数学模型.
2. 理解A,????, φ对函数图象变化的影响,并掌握由y=sinx的图象得到y=Asin(????????+φ)的图象.(难点)
3. 知道函数y=Asin(????????+φ)中常数A,????, φ的物理意义,理解振幅、相位、初相的概念.(重点)
?
课文精讲
问题提出
“南昌之星”摩天轮于2006年竣工,总高度160 m,直径153 m匀速旋转一圈需时30 min.
以摩天轮的中心为原点建立平面直角坐标系,画示意图,如图.
课文精讲
设座舱A为起始位置如图,OA与x轴所形成的角为?????????,因为转一圈需要30 min,所以每分所转的角度为 .
经过x min后,OA旋转到OA′, OA′与x轴所形成角的大小为 .
?
?????????????????????????
?
????????????????=????????????
?
课文精讲
因为直径为153 m,总高度为160 m,所以OA的长为76.5 m,轮子的最低点与地面距离为160-153=7(m),原点O距离地面的距离为7+76.5=83.5(m).从而点A′到地面的距离y与时间x的关系为
y =76.5sin ??????????????????????????+83.5.
?
课文精讲
在物理和工程技术中会遇到一些问题,其中的函数关系都是形如y=Asin(????x+φ)(其中A,????,φ是常数,A>0,????>0)的形式.这类函数有什么性质呢?
从解析式来看,若A=1,????=1, φ =0,函数y=Asin(????x+φ)就是y=sinx.下面,我们就来探究A,????,φ的取值对y=Asin(????x+φ)的图象的影响.
?
课文精讲
实例分析
考虑这类函数的一个特例:y=sin2x,x∈R.
1.周期
由sin2x=sin(2x+2π)= sin 2(x+π),根据周期函数的定义,y=sin2x是周期函数,π是y=
sin2x的最小正周期.
探究????对y=sin????????的图象的影响
?
课文精讲
2.图象
在函数y=sinx五个关键点的基础上,列表(如表).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}2x
0
π
2π
x
0
π
y=sin2x
0
1
0
-1
0
探究????对y=sin????????的图象的影响
?
课文精讲
2.图象
由此得到函数y=sin2x的五个关键点为为 (0,0) (????????,1), (????????,0) ,(????????????,-1), (π,0).
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}2x
0
π
2π
x
0
π
y=sin2x
0
1
0
-1
0
探究????对y=sin????????的图象的影响
?
课文精讲
2.图象
画出该函数在一个周期[0,π]上的图象.由函数y=sin2x的周期性,把图象向左、右延拓,得到y=sin2x在R上的图象(如图).
探究????对y=sin????????的图象的影响
?
课文精讲
2.图象
从函数y=sin2x的图象看出,将函数y=sin x图象上每个点的横坐标都缩短为原来的????????,纵坐标不变,就得到函数y=sin2x的图象(如图),且最小正周期变为π.
?
探究????对y=sin????????的图象的影响
?
课文精讲
3.单调性
从图象上可以看出,函数y=sin2x在区间[kπ ?????????, kπ+ ????????],k∈Z 上单调递增;在区间
[kπ +????????, kπ+ ????????????],k∈Z上单调递减.
?
探究????对y=sin????????的图象的影响
?
课文精讲
4.最大(小)值和值域
在区间[0,π]上,当x=????????时,函数y=sin2x,取得最大值1;当x=????????????时,函数y=sin2x取得最小值-1.由函数y=sin2x的周期性可知,当x=kπ+????????,k∈Z时,它取得最大值1;当x=kπ+????????????,k∈Z时,它取得最小值-1.
?
探究????对y=sin????????的图象的影响
?
课文精讲
4.最大(小)值和值域
函数y=sin2x 的图象夹在两条平行线y=1和y=?1之间,所以它的值域是[-1,1].
?
探究????对y=sin????????的图象的影响
?
典型例题
例1:求函数y=sin????????x的周期,并画出其图象.
?
解:由y=sinx的周期性可知, y=sin????????x=
sin????????????+?????????=sin????????(x+ 6????) .根据周期函数
的定义, y=sin????????x是周期函数, 6????是它的
最小正周期.
?
典型例题
例1:求函数y=sin????????x的周期,并画出其图象.
?
解:在函数y=sinx五个关键点的基础上,列
表(如表).
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
0
π
2π
x
0
6π
0
1
0
-1
0
典型例题
例1:求函数y=sin????????x的周期,并画出其图象.
?
解:于是得到函数y=sin????????x在区间上的五个关
键点为 (0,0) (?????????????,1), (3π,0) ,(????????????,
-1), (6π,0).
?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
0
π
2π
x
0
6π
0
1
0
-1
0
典型例题
例1:求函数y=sin????????x的周期,并画出其图象.
?
解:画出该函数在一个周期[0,6π]上的图象.
由函数y=sin????????x的周期性,把图象向左、
右延拓,得到y=sin????????x 在R上的图象(如图).
?
典型例题
例1:求函数y=sin????????x的周期,并画出其图象.
?
解:从函数y=sin????????x的图象看出,对同一个x值,
将函数y=sinx图象上每个点的横坐标都伸
长到原来的3倍,纵坐标不变,就得到函
数y=sin????????x的图象(如图).
?
课文精讲
一般地,对于????>0,有
sin????x= sin(????x +2π)= sin????????+????????????.
根据周期函数的定义,T=????????????是函数y=sin????x的最小正周期·
?
探究????对y=sin????????的图象的影响
?
课文精讲
函数y=sin????x的图象是将函数y=sinx图象上所有点的横坐标缩短到原来的?????????(当????>1时)或伸长(当0?
探究????对y=sin????????的图象的影响
?
课文精讲
sin(x +φ)的图象
横坐标伸长(0<????<1)或缩短到(????>1)原来的????????倍,纵坐标不变
?
sin(????????+φ)的图象
?
探究????对y=sin????????的图象的影响
?
课文精讲
①????的作用:引起周期T=????????????的改变,这种变换叫
横向伸缩.
?
③函数y=Asin(????x+φ)(????>0,≠1)的图象横向伸
长,周期变大,x的系数变小;横向缩短,周
期变小,x的系数变大.
?
② y=Asin(x+φ)的图象与y=Asin(????x+φ)的图象形
状不同.
?
探究????对y=sin????????的图象的影响
?
课文精讲
考虑这类函数的一个特例: y=sin?????????????.
我们已经知道,函数y=sin?????????????的图象是由函数y=sin????的图象平移得到的.令?????????????=0,得????=????????,即函数y=sin????图象上的点(????,0)向右平移到点(????????,0),所以函数 y=sin?????????????的图象是将函数y=sin????图象上的所有点向右平移????????个单位长度得到的.
?
探究????对y=sin????????的图象的影响
?
课文精讲
从而将刻画函数y=sinx基本形状的五个关键点 (0,0) (????????,1), (π,0) ,(????????????,-1), (2π,0)向右平移??????????个单位长度,得到刻画函数y=sin?????????????基本形状的五个关键点为点 (????????,0),(????????????,1), (????????????,0) ,(????????????????,-1), (????????????,0).
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
画出该函数在一个周期[????????,?????????????]上的图象.由函数y=sin?????????????的周期性,把图延拓到R,得到该函数在R上的图象(如图).
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
从图象上可以看出,函数y=sin??????????????在区间[2kπ?????????, 2kπ+ ????????????],k∈Z上都单调递增;在区间[2kπ+????????????, 2kπ+ ?????????????????],k∈Z上都单调递减.
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
当x=2kπ+????????????,k∈Z时,它取得最大值1;当x=2kπ+ ???????????????? ,k∈Z时,它取得最小值-1.
函数y=sin?????????????的图象夹在两条平行线y=1和y=-1之间,所以它的值域是[-1,1].
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
思考
怎样通过平移函数y=sinx的图象得到y=sin????+?????????的图象?
?
函数y=sinx上的所有点向左平移????????个单位长度得到y=sin????+?????????的图象.
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
概括
函数y=sin(x+φ)与函数y=sinx的周期相同,由x+φ=0,得x=?φ,即函数y=sinx图象上的点(0,0)平移到了点(-φ,0).
函数y=sin(x+φ)的图象,可以看作将函数y=sinx图象上的所有点向左(φ>0)或向右(φ<0)平移|φ|个单位长度得到的.
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
下面来研究函数y=sin????????+??????????的性质.
?
1.周期
y=sin????????+??????????=sin????????+????????+????????=sin[????????+????+????????]
根据周期函数的定义, y=sin????????+??????????是周期函数,π是它的最小正周期. 即函数, y=sin????????+??????????与函数y=sin2x周期相同·
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
2.图象
通过表确定五个关键点.
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}
0
π
2π
x
0
1
0
-1
0
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
2.图象
由此得到在区间[??????????????, ?????????????????????]上刻画该函数基本形状的五个关键点为??????????????,????,??????????,????, ?????????????????,????, ????????????,?????, ????????????????????,????.
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
2.图象
画出函数y=sin????????+??????????在区间[??????????????, ?????????????????????]上的图象.由函数y=sin????????+??????????的周期性,把图象向左、右延拓,就可得到它在R上的图象(如图).
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
2.图象
它也可以由函数y=sin2x的图象向左平移?????????????得到·
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
3.单调性
从图可以看出,函数y=sin????????+??????????在区间[kπ ?????????, kπ+??????????],k∈Z 上单调递增;在区间
[kπ+??????????, kπ+ ????????????],k∈Z上单调递减.
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
4.最大(小)值和值域
当x=kπ+ ?????????,k∈Z时, 函数y=sin????????+??????????取得最大值1;当x=kπ+????????????,k∈Z时,它取得最小值-1.
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
4.最大(小)值和值域
函数y=sin??????????????????的图象夹在两条平行线y=1和y=?1之间,所以它的值域是[-1,1].
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
概括
函数y=sin(????x +φ)与函数y=sin????x有相同的周期,由????x +φ =0,得x=?????????,即函数y=sin????x 图象上的点(0,0)平移到点(??????????,0).函数y=sin(????x +φ)的图象,可以看作将函数y=sin????x图象上的所有点向左(φ>0)向右(φ<0)平移|????????|个单位长度得到的.
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
概括
在函数y=sin(????x +φ)中, φ决定了x=0时的函数值,通常称φ为初相,????x +φ为相位.
?
探究????对y=sin(x+φ)的图象的影响
?
课文精讲
概括
①φ的变化引起图象位置的变化.
② y=sin(x+φ)的图象与y=sinx的图象形状完全
一样,且由y=sinx的图象向左(右)平移得到;
y=sinx的图象
探究????对y=sin(x+φ)的图象的影响
?
向左(φ>0)或向右(φ<0)平移| φ |个单位长度
y=sin(x+φ)的图象
课文精讲
谢 谢
课文精讲
探究????对y=Asin(????x+φ)的图象的影响
?
探究函数y=2sin????????+????????的周期,并画出它的图象.
?
函数y=2sin????????+?????????与函数y=sin????????+?????????有相同的周期,即它的周期是π.
?
课文精讲
前面已经画出了函数y=2sin????????+?????????的图象,并讨论了它的性质,所以从解析表达式上容易得到,对于同一个x值,函数y=2sin????????+?????????图象上点的纵坐标等于函数y=sin????????+?????????图象上点的纵坐标的2倍.
?
探究????对y=Asin(????x+φ)的图象的影响
?
课文精讲
这表明,函数y=2sin????????+????????的图象,可以看作是将函数y=sin????????+????????图象上所有点的纵坐标伸长到原来的2倍(横坐标不变)而得到的.
?
探究????对y=Asin(????x+φ)的图象的影响
?
课文精讲
如图.
探究????对y=Asin(????x+φ)的图象的影响
?
课文精讲
概括
y=Asin(????x +φ)(A>0)的图象是将y=sin(????x +φ)的图象上的每个点的纵坐标伸长(当A>1时)
或缩短(当0
探究????对y=Asin(????x+φ)的图象的影响
?
课文精讲
如何更好的理解呢?
①若A>0,则函数y=Asin(????x +φ)的值域为 [-A ,A],最大值为A,最小值为-A.
若A <0,则函数y=Asin(????x +φ)的值域为
[A ,-A] ,最大值为-A,最小值为A.
?
探究????对y=Asin(????x+φ)的图象的影响
?
②A的作用:引起值域的改变,这种变换叫
纵向伸缩.
课文精讲
如何更好的理解呢?
③|A|的大小反映了曲线y=Asin(????x +φ)的波
动幅度的大小.
?
探究????对y=Asin(????x+φ)的图象的影响
?
④y=Asin(????x +φ)与y=sin(????x +φ)的图象形状
不同.
?
课文精讲
思考
函数y=2sin????????+?????????+1与函数y=sin????????+?????????的图象有什么不同?
?
探究????对y=Asin(????x+φ)的图象的影响
?
课文精讲
综上关于????,φ,A这三个参数的讨论,可知探究函数y=Asin(????x+φ)(A>0,????>0,x∈R)性质的一般步骤:
第1步,确定周期T=????????????;
第2步,在y=sinx五个关键点(0,0),????????,????,
(????,????), ????????????,?????, ????????,???? 的基础上确定该函数的五个关键点;
?
探究????对y=Asin(????x+φ)的图象的影响
?
课文精讲
综上关于????,φ ,A这三个参数的讨论,可知探究函数y=Asin(????x+φ)(A>0,????>0,x∈R)性质的一般步骤:
第3步,用光滑曲线顺次连接五个关键点,即可画出函数y=Asin(????x+φ)(在一个周期上的图象,再利用其周期性把图象延拓到R,就可以得到它在R上的图象;
?
探究????对y=Asin(????x+φ)的图象的影响
?
课文精讲
综上关于????,φ ,A这三个参数的讨论,可知探究函数y=Asin(????x+φ)(A>0,????>0,x∈R)性质的一般步骤:
第4步,借助图象讨论性质.
实际上,这也是讨论周期函数的一般方法和步骤.
?
探究????对y=Asin(????x+φ)的图象的影响
?
课文精讲
步骤1
由y=sinx的图象得到y=Asin(????????+ φ ) (A>0,????>0)的图象的两种方法:
?
画出y=sinx的图象
得到y=sin(????+φ )的图象
?
得到y=sin(????????+ φ )的图象
?
得到y=Asin(????????+φ)的图象
?
向左(右)平移
| φ |个单位长度
步骤2
步骤3
步骤4
横坐标变为原来的????????倍
?
纵坐标变为原来的????倍
?
探究????对y=Asin(????x+φ)的图象的影响
?
课文精讲
由y=sinx的图象得到y=Asin(????????+ φ ) (A>0,????>0)的图象的两种方法:
?
步骤1
画出y=sinx的图象
得到y=sin????????的图象
?
得到y=sin(????????+ φ )的图象
?
得到y=Asin(????????+ φ)的图象
?
向左(右)平移|????|????个单位长度
?
步骤2
步骤3
步骤4
横坐标变为原来的????????倍
?
纵坐标变为原来的????倍
?
探究????对y=Asin(????x+φ)的图象的影响
?
典型例题
例2:画出函数y=cos????????????的图象,并讨论其基本性质.
?
解:方法一:
直接运用y=Asin(????x+φ)的结果,先变形,
y=cos????????????=sin??????????????????????=sin?????????????+????????,
再用上面的一般方法来研究.
?
典型例题
例2:画出函数y=cos????????????的图象,并讨论其基本性质.
?
解:方法二:使用类似y=Asin(????x+φ)的研究方法
(1)周期
因为y=cos????的周期是2π,所以cos????????????=
cos????????????+????????= cos???????? (x+4π),该函数的周期
为T=4π.
?
典型例题
例2:画出函数y=cos????????????的图象,并讨论其基本性质.
?
解:方法二:使用类似y=Asin(????x+φ)的研究方法
(2)图象
刻画函数y=cos????在区间[0,2π]上图象基
本形状的五个关键点为(0,1),????????,????,
(????,?????), ????????????,????, ????????,????.
?
典型例题
例2:画出函数y=cos????????????的图象,并讨论其基本性质.
?
解:方法二:使用类似y=Asin(????x+φ)的研究方法
(2)图象
由此得到刻画函数y=cos????????????在区间[0,
4π]上图象基本形状的五个关键点为(0,1),
?????????(????,????) , (????????,?????), ????????,????,
????????,????.
?
典型例题
例2:画出函数y=cos????????????的图象,并讨论其基本性质.
?
解:方法二:使用类似y=Asin(????x+φ)的研究方法
(2)图象
用光滑曲线顺次连接五个关键点画出函
数y=cos????????????在区间[0,4π]上的图象.由它的周
期性,把图象向左、右延拓,就可以得到它
在R上的图象(如图).
?
典型例题
例2:画出函数y=cos????????????的图象,并讨论其基本性质.
?
解:方法二:使用类似y=Asin(????x+φ)的研究方法
(2)图象
?
典型例题
例2:画出函数y=cos????????????的图象,并讨论其基本性质.
?
解:方法二:使用类似y=Asin(????x+φ)的研究方法
(3)其他性质
设????=????????????,则函数y=cosu的单调递增
区间[2kπ-π,2kπ],k∈Z.
由2kπ-π≤ ???????????? ≤ 2kπ,k∈Z,得4kπ-2π
≤ ????≤???????????? , k∈Z.
?
典型例题
例2:画出函数y=cos????????????的图象,并讨论其基本性质.
?
解:方法二:使用类似y=Asin(????x+φ)的研究方法
(3)其他性质
?
所以函数y=cos????????????的单调递增区间是[4kπ-2π,4kπ],k∈Z.
类似地,函数y=cos????????????的单调递减区间是[4kπ,4kπ+2π],k∈Z.
?
典型例题
例2:画出函数y=cos????????????的图象,并讨论其基本性质.
?
解:方法二:使用类似y=Asin(????x+φ)的研究方法
(3)其他性质
?
函数y=cosu,u∈R取得最大值的u的集合是{u| u= 2kπ,k∈Z}.
典型例题
例2:画出函数y=cos????????????的图象,并讨论其基本性质.
?
解:方法二:使用类似y=Asin(????x+φ)的研究方法
(3)其他性质
?
由?????????????= 2kπ ,得x= 4kπ,k∈Z,所以当x∈{x|x= 4kπ,k∈Z}时,函数y=cos????????????, x∈R取得最大值1.
?
典型例题
例2:画出函数y=cos????????????的图象,并讨论其基本性质.
?
解:方法二:使用类似y=Asin(????x+φ)的研究方法
(3)其他性质
?
类似地,当x∈{x|x= 4kπ+ 2π,k∈Z}时,函数y=cos????????????, x∈R取得最小值-1.
?
函数y=cos?????????????, x∈R的值域为[-1,1].
?
综合练习
若函数y=sin(2x + ????????) ,则它的最小正周期T=______.
?
解:T=????????????=????.
?
????
?
综合练习
已知函数f(x)=2sin(2x + ????????).
(1)求函数在[0,π]的单调递增区间;
(2)关于x的不等式f(x)<1的解集.
?
解: (1)令2kπ- ?????????≤2x + ????????≤2kπ+ ????????,
解得kπ- ?????????????????≤x≤kπ+????????????, k∈Z,
故 f(x)的单调递增区间[kπ- ?????????????????, kπ+????????????],
?
综合练习
已知函数f(x)=2sin(2x + ????????).
(1)求函数在[0,π]的单调递增区间;
(2)关于x的不等式f(x)<1的解集.
?
解:(1) 令k=0,单调递增区间为[-????????????????,????????????] ,
令k=1,单调递增区间为[????????????????,????????????????????],
故f(x)在[0,π]上的单调递增区间为[????,????????????] ∪[????????????????,????].
?
综合练习
已知函数f(x)=2sin(2x + ????????).
(1)求函数在[0,π]的单调递增区间;
(2)关于x的不等式f(x)<1的解集.
?
解: (2) 由f(x)=2sin(2x + ????????)<1得:
sin(2x + ????????)<????????,
故2kπ+ ?????????????<2x + ????????≤2kπ+ ????????????????,k∈Z,
解得:kπ+ ?????????<x≤kπ+ ????????????????????,k∈Z,
?
综合练习
已知函数f(x)=2sin(2x + ????????).
(1)求函数在[0,π]的单调递增区间;
(2)关于x的不等式f(x)<1的解集.
?
解: (2)所以f(x)<1的解集为:
(kπ+ ?????????, kπ+ ????????????????????).
?
本课小结
再 见
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
