7.3三角形-2020-2021学年苏科版七年级数学下册专题复习提升训练(含答案)
文档属性
| 名称 | 7.3三角形-2020-2021学年苏科版七年级数学下册专题复习提升训练(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 774.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-09 23:34:59 | ||
图片预览

文档简介
专题复习提升训练卷7.3三角形-20-21苏科版七年级数学下册
一、选择题
1、对图理解错误的是 ( )
A.∠A,∠B,∠ACB是△ABC的内角 B.∠BCD是与∠ACB相邻的外角
C.∠BCD+∠A=180° D.△ABC的三条边分别是线段AB,BC,AC
(2) (6) (7)
2、如图,在△ABC中有四条线段DE,BE,EG,FG,其中有一条线段是△ABC的中线,则该线段是 ( )
A.DE B.BE C.EG D.FG
3、若△ABC的一个外角为50°,则△ABC一定是 ( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.锐角三角形或钝角三角形
4、下列说法正确的是 ( )
A.一个直角三角形一定不是等腰三角形 B.一个等腰三角形一定不是锐角三角形
C.一个钝角三角形一定不是等腰三角形 D.一个等边三角形一定不是钝角三角形
5、下列说法不正确的是 ( )
A.三角形的中线在三角形的内部 B.三角形的角平分线在三角形的内部
C.三角形的高都在三角形的内部 D.三角形必有一条高在三角形的内部
6、如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于点E,F为AB上的一点,CF⊥AD于点H.
下列说法正确的是 ( )
A.AD是△ABE的角平分线 B.BE是△ABD中边AD上的中线
C.CH为△ACD中边AD上的高 D.AH为△ABC的角平分线
7、如图,在三角形ABC中,,,AD平分交BC于D,DE?AB交AC于E,
则的大小是( )
A.45° B.54° C.39° D.50°
8、如图,在△ABC中,∠BAC=60°,BD、CE分别平分∠ABC、∠ACB,BD、CE相交于点O,
则∠BOC的度数是( )
A.120° B.130° C.75° D.150°
(9) (10) (11)
9、如图,已知 AB//CD,则( )
A.∠1=∠2+∠3 B.∠1=2∠2+∠3 C.∠1=2∠2-∠3 D.∠1=180°-∠2-∠3
10、如图,已知//b,那么下列式子中,结果等于180°的是 ( )
A.+β+γ B.+β-γ C.-+β+γ D.-β+γ
11、小明把一副含45、30°角的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D =30°,
则∠α+∠β等于( )
A.180° B.210° C.360° D.270°
12、如图,AB和CD相交于点O,∠A=∠C,则下列结论中不能完全确定正确的是( )
A.∠B=∠D B.∠1=∠A+∠D C.∠2>∠D D.∠C=∠D
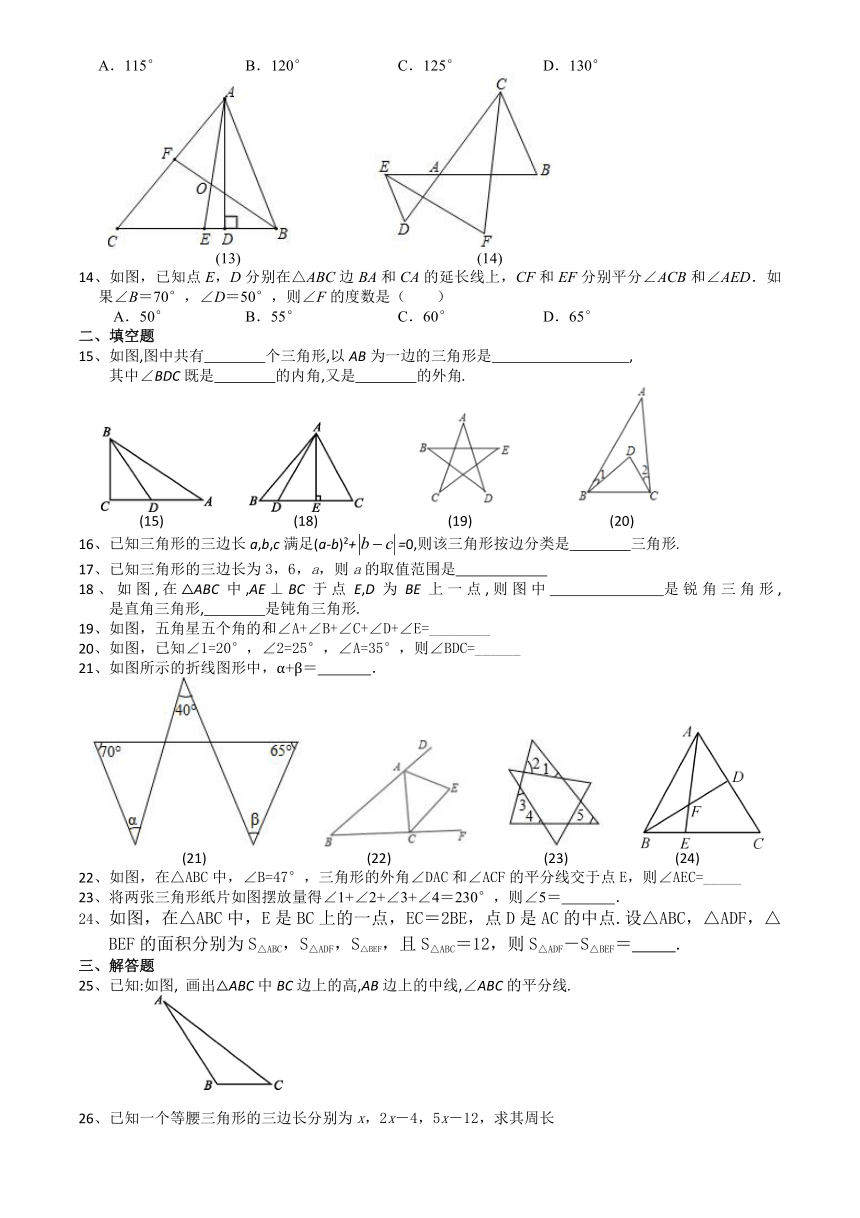
13、如图,在△ABC中,AD是高,AE、BF是两内角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数之和为( )
A.115° B.120° C.125° D.130°
(14)
14、如图,已知点E,D分别在△ABC边BA和CA的延长线上,CF和EF分别平分∠ACB和∠AED.如果∠B=70°,∠D=50°,则∠F的度数是( )
A.50° B.55° C.60° D.65°
二、填空题
15、如图,图中共有 个三角形,以AB为一边的三角形是 ,
其中∠BDC既是 的内角,又是 的外角.?
(15) (18) (19) (20)
16、已知三角形的三边长a,b,c满足(a-b)2+=0,则该三角形按边分类是 三角形.
17、已知三角形的三边长为3,6,a,则a的取值范围是
18、如图,在△ABC中,AE⊥BC于点E,D为BE上一点,则图中 是锐角三角形, 是直角三角形, 是钝角三角形.
19、如图,五角星五个角的和∠A+∠B+∠C+∠D+∠E=________
20、如图,已知∠1=20°,∠2=25°,∠A=35°,则∠BDC=______
21、如图所示的折线图形中,α+β= .
(22) (23) (24)
22、如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=_____
23、将两张三角形纸片如图摆放量得∠1+∠2+∠3+∠4=230°,则∠5= .
24、如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点.设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF-S△BEF= .
三、解答题
25、已知:如图, 画出△ABC中BC边上的高,AB边上的中线,∠ABC的平分线.
26、已知一个等腰三角形的三边长分别为x,2x-4,5x-12,求其周长
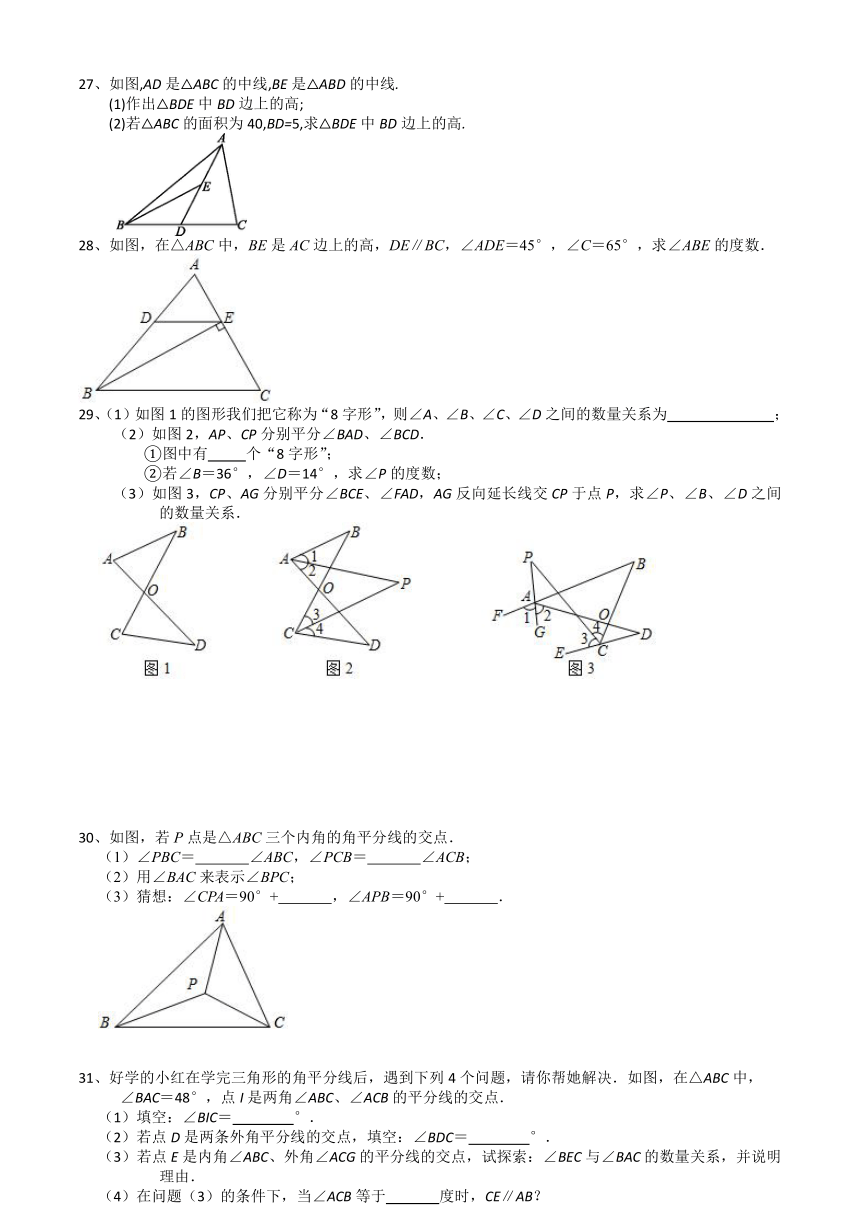
27、如图,AD是△ABC的中线,BE是△ABD的中线.
(1)作出△BDE中BD边上的高;
(2)若△ABC的面积为40,BD=5,求△BDE中BD边上的高.
28、如图,在△ABC中,BE是AC边上的高,DE∥BC,∠ADE=45°,∠C=65°,求∠ABE的度数.
29、(1)如图1的图形我们把它称为“8字形”,则∠A、∠B、∠C、∠D之间的数量关系为 ;
(2)如图2,AP、CP分别平分∠BAD、∠BCD.
①图中有 个“8字形”;
②若∠B=36°,∠D=14°,求∠P的度数;
(3)如图3,CP、AG分别平分∠BCE、∠FAD,AG反向延长线交CP于点P,求∠P、∠B、∠D之间的数量关系.
30、如图,若P点是△ABC三个内角的角平分线的交点.
(1)∠PBC= ∠ABC,∠PCB= ∠ACB;
(2)用∠BAC来表示∠BPC;
(3)猜想:∠CPA=90°+ ,∠APB=90°+ .
31、好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决.如图,在△ABC中,
∠BAC=48°,点I是两角∠ABC、∠ACB的平分线的交点.
(1)填空:∠BIC= °.
(2)若点D是两条外角平分线的交点,填空:∠BDC= °.
(3)若点E是内角∠ABC、外角∠ACG的平分线的交点,试探索:∠BEC与∠BAC的数量关系,并说明理由.
(4)在问题(3)的条件下,当∠ACB等于 度时,CE∥AB?
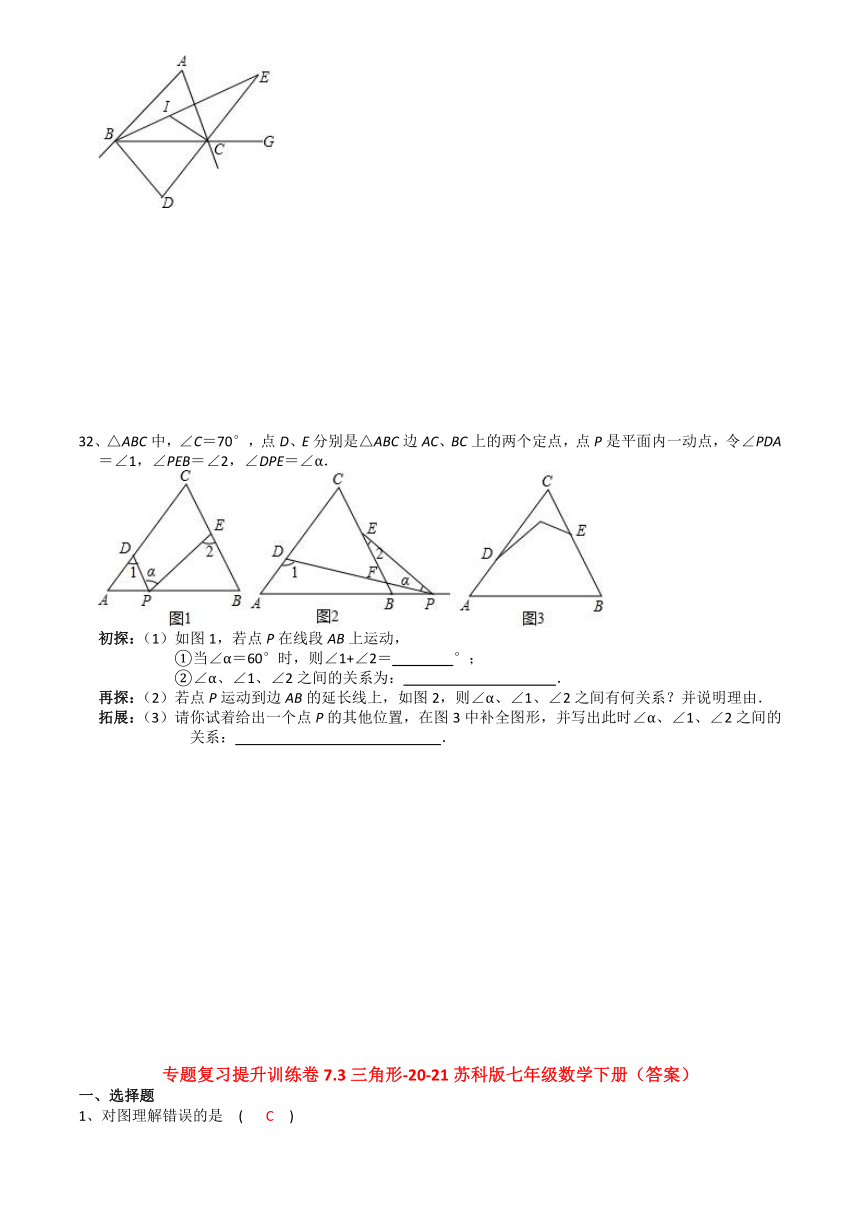
32、△ABC中,∠C=70°,点D、E分别是△ABC边AC、BC上的两个定点,点P是平面内一动点,令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
初探:(1)如图1,若点P在线段AB上运动,
①当∠α=60°时,则∠1+∠2= °;
②∠α、∠1、∠2之间的关系为: .
再探:(2)若点P运动到边AB的延长线上,如图2,则∠α、∠1、∠2之间有何关系?并说明理由.
拓展:(3)请你试着给出一个点P的其他位置,在图3中补全图形,并写出此时∠α、∠1、∠2之间的关系: .
专题复习提升训练卷7.3三角形-20-21苏科版七年级数学下册(答案)
一、选择题
1、对图理解错误的是 ( C )
A.∠A,∠B,∠ACB是△ABC的内角 B.∠BCD是与∠ACB相邻的外角
C.∠BCD+∠A=180° D.△ABC的三条边分别是线段AB,BC,AC
2、如图,在△ABC中有四条线段DE,BE,EG,FG,其中有一条线段是△ABC的中线,则该线段是 ( B )
A.DE B.BE C.EG D.FG
3、若△ABC的一个外角为50°,则△ABC一定是 ( B )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.锐角三角形或钝角三角形
4、下列说法正确的是 ( D )
A.一个直角三角形一定不是等腰三角形 B.一个等腰三角形一定不是锐角三角形
C.一个钝角三角形一定不是等腰三角形 D.一个等边三角形一定不是钝角三角形
5、下列说法不正确的是 ( C )
A.三角形的中线在三角形的内部 B.三角形的角平分线在三角形的内部
C.三角形的高都在三角形的内部 D.三角形必有一条高在三角形的内部
6、如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于点E,F为AB上的一点,CF⊥AD于点H.
下列说法正确的是 ( C )
A.AD是△ABE的角平分线 B.BE是△ABD中边AD上的中线
C.CH为△ACD中边AD上的高 D.AH为△ABC的角平分线
7、如图,在三角形ABC中,,,AD平分交BC于D,DE?AB交AC于E,
则的大小是( )
A.45° B.54° C.39° D.50°
解:∵,∴∠BAC=180°-
∵AD平分,∴∠BAD=∠BAC=39°
∵DE?AB,∴==,故选C.
8、如图,在△ABC中,∠BAC=60°,BD、CE分别平分∠ABC、∠ACB,BD、CE相交于点O,
则∠BOC的度数是( )
A.120° B.130° C.75° D.150°
解:∵∠BAC=60°,∴∠ABC+∠ACB=,
∵BD,CE分别平分∠ABC,∠ACB, ∴OBC=ABC,OCB=ACB,
∴OBC+OCB=(∠ABC+ACB)
∴∠BOC=180°-(∠ABC+∠ACB)=180°-×=120°.
故选:A.
9、如图,已知 AB//CD,则( A )
A.∠1=∠2+∠3 B.∠1=2∠2+∠3 C.∠1=2∠2-∠3 D.∠1=180°-∠2-∠3
10、如图,已知//b,那么下列式子中,结果等于180°的是 ( B )
A.+β+γ B.+β-γ C.-+β+γ D.-β+γ
11、小明把一副含45、30°角的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D =30°,
则∠α+∠β等于( B )
A.180° B.210° C.360° D.270°
12、如图,AB和CD相交于点O,∠A=∠C,则下列结论中不能完全确定正确的是( )
A.∠B=∠D B.∠1=∠A+∠D C.∠2>∠D D.∠C=∠D
解:∵∠A+∠AOD+∠D=180°,∠C+∠COB+∠B=180°,∠A=∠C,∠AOD=∠BOC,
∴∠B=∠D,
∵∠1=∠2=∠A+∠D,
∴∠2>∠D,
故选项A,B,C正确,
故选:D.
13、如图,在△ABC中,AD是高,AE、BF是两内角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数之和为( )
A.115° B.120° C.125° D.130°
解:∵∠CAB=50°,∠C=60°∴∠ABC=180°﹣50°﹣60°=70°,
又∵AD是高,∴∠ADC=90°,∴∠DAC=180°﹣90°﹣∠C=30°,
∵AE、BF是角平分线,∴∠CBF=∠ABF=35°,∠EAF=25°,
∴∠DAE=∠DAC﹣∠EAF=5°,∠AFB=∠C+∠CBF=60°+35°=95°,
∴∠BOA=∠EAF+∠AFB=25°+95°=120°,
∴∠DAE+∠BOA=5°+120°=125°.故选:C.
14、如图,已知点E,D分别在△ABC边BA和CA的延长线上,CF和EF分别平分∠ACB和∠AED.如果∠B=70°,∠D=50°,则∠F的度数是( )
A.50° B.55° C.60° D.65°
解:如图,设AB交CF于点G,
∵CF、EF分别平分∠ACB和∠AED, ∴∠BCF=∠ACF,∠DEF=∠AEF,
∵∠BCF+∠B=∠AEF+∠F;∠BCF+∠ACF+∠B=∠DEF+∠AEF+∠D,
即2∠BCF+∠B=2∠AEF+∠D,
又∵∠B=70°,∠D=50°,
∴∠BCF+70°=∠AEF+∠F①,2∠BCF+70°=2∠AEF+50°②,
①×2﹣②得,70°=2∠F﹣50°,
解得∠F=60°.
故选:C.
二、填空题
15、如图,图中共有 个三角形,以AB为一边的三角形是 ,
其中∠BDC既是 的内角,又是 的外角.?
答案: 3 △ABC, △ABD △BCD △ABD
16、已知三角形的三边长a,b,c满足(a-b)2+=0,则该三角形按边分类是 等边 三角形.
17、已知三角形的三边长为3,6,a,则a的取值范围是 318、如图,在△ABC中,AE⊥BC于点E,D为BE上一点,则图中 是锐角三角形, 是直角三角形, 是钝角三角形.
答案: △ABC,△ADC △ADE,△ACE,△ABE △ABD
19、如图,五角星五个角的和∠A+∠B+∠C+∠D+∠E=___180°_____
20、如图,已知∠1=20°,∠2=25°,∠A=35°,则∠BDC=__80°_____
21、如图所示的折线图形中,α+β= .
解:方法一:如图,连接BC.
在△EBC中,∠1+∠2=180°﹣∠E=140°,
在四边形ABCD中,∠A+∠ABC+∠BCD+∠D=360°,
∴70°+α+∠1+∠2+β+65°=360°,
∴α+β=360°﹣70°﹣65°﹣140°=85°,
方法二:∵α+70=40+?4,
β+65=40+?3
∴α+70+β+65=40+?4+40+?3
∴α+β=40+180-70-65=85°
故答案为85°.
22、如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=__66.5°___
23、将两张三角形纸片如图摆放量得∠1+∠2+∠3+∠4=230°,则∠5= .
解:如图所示:∠1+∠2+∠6=180°,∠3+∠4+∠7=180°,
∵∠1+∠2+∠3+∠4=230°,∴∠1+∠2+∠6+∠3+∠4+∠7=360°,∴∠6+∠7=130°,
∴∠5=180°﹣(∠6+∠7)=50°. 故答案为:50°.
24、如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点.设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF-S△BEF=2 .
三、解答题
25、已知:如图, 画出△ABC中BC边上的高,AB边上的中线,∠ABC的平分线.
解: 如图所示.(1)过点A画AD⊥CB交CB的延长线于点D,则AD即为△ABC的BC边上的高.
(2)画AB边的中点F,连结CF,则CF即为AB边的中线.
(3)画BE平分∠ABC交AC于点E,则线段BE即为∠ABC的平分线.
26、已知一个等腰三角形的三边长分别为x,2x-4,5x-12,求其周长=_________
解:①当x=2x-4时,x=4,即三边长为4,4,8.此时不能构成三角形;
②当x=5x-12时,x=3,即三边长为3,2,3,其周长为8;
③当2x-4=5x-12时,x=,
即三边长为,,,不能构成三角形.
故三角形周长为8.
27、如图,AD是△ABC的中线,BE是△ABD的中线.
(1)作出△BDE中BD边上的高;
(2)若△ABC的面积为40,BD=5,求△BDE中BD边上的高.
解:(1)如图, EF为△BDE中BD边上的高
(2)因为AD是△ABC的中线,所以S△ABD=S△ABC.
同理,S△BDE=S△ABD, 所以S△BDE=S△ABC.
因为S△BDE=BD·EF,所以BD·EF=S△ABC.
又因为△ABC的面积为40,BD=5, 所以EF=4.
即△BDE中BD边上的高是4.
28、如图,在△ABC中,BE是AC边上的高,DE∥BC,∠ADE=45°,∠C=65°,求∠ABE的度数.
解:∵DE∥BC,∠ADE=45°,∴∠ABC=∠ADE=45°,
∵BE是AC边上的高,∴∠BEC=90°,
∵∠C=65°,∴∠EBC=90°﹣∠C=25°,
∴∠ABE=∠ABC﹣∠EBC=45°﹣25°=20°.
29、(1)如图1的图形我们把它称为“8字形”,则∠A、∠B、∠C、∠D之间的数量关系为 ;
(2)如图2,AP、CP分别平分∠BAD、∠BCD.
①图中有 个“8字形”;
②若∠B=36°,∠D=14°,求∠P的度数;
(3)如图3,CP、AG分别平分∠BCE、∠FAD,AG反向延长线交CP于点P,求∠P、∠B、∠D之间的数量关系.
【解析】(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180°,
又∵∠AOB=∠COD,∴∠A+∠B=∠C+∠D, 故答案为:∠A+∠B=∠C+∠D.
(2)①图中,有6个“8字形”. 故答案为6.
②∵AP平分∠BAD,∴∠1=∠2, ∵PC平分∠BCD,∴∠3=∠4,
∵∠1+∠B=∠3+∠P①, ∠2+∠P=∠4+∠D②,
①﹣②得,2∠P=∠B+∠D=50°,∴∠P=25°.
(3)结论:2∠P=∠B+∠D.
理由:∵CP平分∠BCE,∴∠3=∠4,
∵AG平分∠DAF,∴∠1=∠2, ∵∠PAB=∠1,∴∠2=∠PAB,
∵∠P+∠PAB=∠B+∠4, ∴∠P+∠2=∠B+∠4 ③,
∵∠P+∠PAD=∠D+∠PCD,∴∠P+(180°﹣∠2)=∠D+(180°﹣∠3)④,
③+④得,2∠P=∠B+∠D.
30、如图,若P点是△ABC三个内角的角平分线的交点.
(1)∠PBC= ∠ABC,∠PCB= ∠ACB;
(2)用∠BAC来表示∠BPC;
(3)猜想:∠CPA=90°+ ,∠APB=90°+ .
解:(1)∵P点是△ABC三个内角的角平分线的交点,
∴∠PBC=∠ABC,∠PCB=∠ACB,
故答案为:,;
(2)∵∠PBC=∠ABC,∠PCB=∠ACB,
∴∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠BAC)=180°﹣90°+∠BAC=90°+∠BAC;
(3)猜想:∠CPA=90°+∠ABC,∠APB=90°+∠ACB;
理由如下:∵AP平分∠BAC,CP平分∠ACB
∴∠PAC=,∠ACP=
∴∠CPA=180°﹣(∠PAC+∠ACP)=180°﹣(∠BAC+∠ACB)
=180°﹣(1800﹣∠ABC)=180°﹣90°+∠ABC=90°+∠ABC;
同理可得:∠APB=90°+∠ACB.
故答案为:,∠ACB.
31、好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决.如图,在△ABC中,
∠BAC=48°,点I是两角∠ABC、∠ACB的平分线的交点.
(1)填空:∠BIC= °.
(2)若点D是两条外角平分线的交点,填空:∠BDC= °.
(3)若点E是内角∠ABC、外角∠ACG的平分线的交点,试探索:∠BEC与∠BAC的数量关系,并说明理由.
(4)在问题(3)的条件下,当∠ACB等于 度时,CE∥AB?
【解析】(1)∵∠A=48°,∴∠ABC+∠ACB=180°﹣48°=132°,
∵点I是两角∠ABC、∠ACB的平分线的交点,
∴∠IBC+∠ICB=(∠ABC+∠ACB)=66°,
∴∠BIC=180°﹣66°=114°.故答案为114.
(2)由题意:∠IBD=∠ICD=90°,∴∠BDC+∠BIC=180°,
∴∠BDC=66°.故答案为66.
(3)设∠ACE=∠ECG=x,∠ABI=∠IBC=y,
∴2x=2y+∠A①,
x=y+∠E②,
①÷2﹣②可得∠E=∠A.
(4)∵CE∥AB,∴∠ECA=∠A=48°,
∴∠ECG=∠ECA=∠ABC=48°,
∴∠ACB=180°﹣48°﹣48°=84°, 故答案为84.
32、△ABC中,∠C=70°,点D、E分别是△ABC边AC、BC上的两个定点,点P是平面内一动点,令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
初探:(1)如图1,若点P在线段AB上运动,
①当∠α=60°时,则∠1+∠2= °;
②∠α、∠1、∠2之间的关系为: .
再探:(2)若点P运动到边AB的延长线上,如图2,则∠α、∠1、∠2之间有何关系?并说明理由.
拓展:(3)请你试着给出一个点P的其他位置,在图3中补全图形,并写出此时∠α、∠1、∠2之间的关系: .
【解析】(1)①如图1中,连接PC.∵∠1=∠DCP+∠DPC,∠2=∠ECP+∠CPE,
∴∠1+∠2=∠DCP+∠DCP+∠ECP+∠EPC=∠ACB+∠DPE=∠ACB+∠α,
∵∠ACB=70°,∠α=60°,∴∠1+∠2=60°+70°=130°.
②由①可知,∠1+∠2=∠ACB+∠α=70°+∠α,
故答案为130,70°+∠α.
(2)结论:∠1=70°+∠2+∠α.
理由:如图2中,∵∠1=∠C+∠CFD,∠CFD=∠2+∠α,∴∠1=70°+∠2+∠α.
(3)结论:∠1+∠2=430°﹣∠α.
理由:如图3中,∵∠1=∠DCP+∠DPC,∠2=∠ECP+∠CPE,
∴∠1+∠2=∠DCP+∠DPC+∠ECP+∠EPC=∠ACB+360°﹣∠DPE=70°+360°﹣∠α,
∴∠1+∠2=430°﹣∠α.
故答案为∠1+∠2=430°﹣∠α.
一、选择题
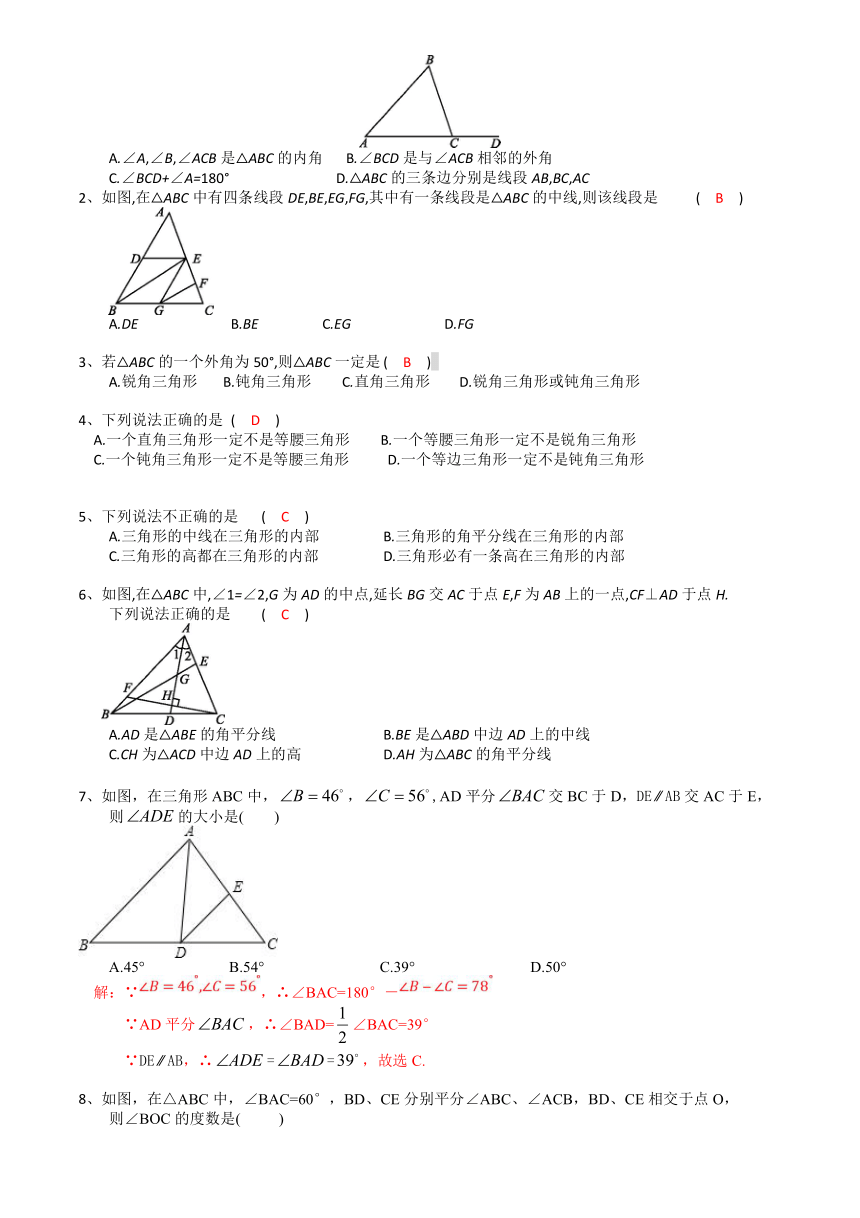
1、对图理解错误的是 ( )
A.∠A,∠B,∠ACB是△ABC的内角 B.∠BCD是与∠ACB相邻的外角
C.∠BCD+∠A=180° D.△ABC的三条边分别是线段AB,BC,AC
(2) (6) (7)
2、如图,在△ABC中有四条线段DE,BE,EG,FG,其中有一条线段是△ABC的中线,则该线段是 ( )
A.DE B.BE C.EG D.FG
3、若△ABC的一个外角为50°,则△ABC一定是 ( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.锐角三角形或钝角三角形
4、下列说法正确的是 ( )
A.一个直角三角形一定不是等腰三角形 B.一个等腰三角形一定不是锐角三角形
C.一个钝角三角形一定不是等腰三角形 D.一个等边三角形一定不是钝角三角形
5、下列说法不正确的是 ( )
A.三角形的中线在三角形的内部 B.三角形的角平分线在三角形的内部
C.三角形的高都在三角形的内部 D.三角形必有一条高在三角形的内部
6、如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于点E,F为AB上的一点,CF⊥AD于点H.
下列说法正确的是 ( )
A.AD是△ABE的角平分线 B.BE是△ABD中边AD上的中线
C.CH为△ACD中边AD上的高 D.AH为△ABC的角平分线
7、如图,在三角形ABC中,,,AD平分交BC于D,DE?AB交AC于E,
则的大小是( )
A.45° B.54° C.39° D.50°
8、如图,在△ABC中,∠BAC=60°,BD、CE分别平分∠ABC、∠ACB,BD、CE相交于点O,
则∠BOC的度数是( )
A.120° B.130° C.75° D.150°
(9) (10) (11)
9、如图,已知 AB//CD,则( )
A.∠1=∠2+∠3 B.∠1=2∠2+∠3 C.∠1=2∠2-∠3 D.∠1=180°-∠2-∠3
10、如图,已知//b,那么下列式子中,结果等于180°的是 ( )
A.+β+γ B.+β-γ C.-+β+γ D.-β+γ
11、小明把一副含45、30°角的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D =30°,
则∠α+∠β等于( )
A.180° B.210° C.360° D.270°
12、如图,AB和CD相交于点O,∠A=∠C,则下列结论中不能完全确定正确的是( )
A.∠B=∠D B.∠1=∠A+∠D C.∠2>∠D D.∠C=∠D
13、如图,在△ABC中,AD是高,AE、BF是两内角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数之和为( )
A.115° B.120° C.125° D.130°
(14)
14、如图,已知点E,D分别在△ABC边BA和CA的延长线上,CF和EF分别平分∠ACB和∠AED.如果∠B=70°,∠D=50°,则∠F的度数是( )
A.50° B.55° C.60° D.65°
二、填空题
15、如图,图中共有 个三角形,以AB为一边的三角形是 ,
其中∠BDC既是 的内角,又是 的外角.?
(15) (18) (19) (20)
16、已知三角形的三边长a,b,c满足(a-b)2+=0,则该三角形按边分类是 三角形.
17、已知三角形的三边长为3,6,a,则a的取值范围是
18、如图,在△ABC中,AE⊥BC于点E,D为BE上一点,则图中 是锐角三角形, 是直角三角形, 是钝角三角形.
19、如图,五角星五个角的和∠A+∠B+∠C+∠D+∠E=________
20、如图,已知∠1=20°,∠2=25°,∠A=35°,则∠BDC=______
21、如图所示的折线图形中,α+β= .
(22) (23) (24)
22、如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=_____
23、将两张三角形纸片如图摆放量得∠1+∠2+∠3+∠4=230°,则∠5= .
24、如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点.设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF-S△BEF= .
三、解答题
25、已知:如图, 画出△ABC中BC边上的高,AB边上的中线,∠ABC的平分线.
26、已知一个等腰三角形的三边长分别为x,2x-4,5x-12,求其周长
27、如图,AD是△ABC的中线,BE是△ABD的中线.
(1)作出△BDE中BD边上的高;
(2)若△ABC的面积为40,BD=5,求△BDE中BD边上的高.
28、如图,在△ABC中,BE是AC边上的高,DE∥BC,∠ADE=45°,∠C=65°,求∠ABE的度数.
29、(1)如图1的图形我们把它称为“8字形”,则∠A、∠B、∠C、∠D之间的数量关系为 ;
(2)如图2,AP、CP分别平分∠BAD、∠BCD.
①图中有 个“8字形”;
②若∠B=36°,∠D=14°,求∠P的度数;
(3)如图3,CP、AG分别平分∠BCE、∠FAD,AG反向延长线交CP于点P,求∠P、∠B、∠D之间的数量关系.
30、如图,若P点是△ABC三个内角的角平分线的交点.
(1)∠PBC= ∠ABC,∠PCB= ∠ACB;
(2)用∠BAC来表示∠BPC;
(3)猜想:∠CPA=90°+ ,∠APB=90°+ .
31、好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决.如图,在△ABC中,
∠BAC=48°,点I是两角∠ABC、∠ACB的平分线的交点.
(1)填空:∠BIC= °.
(2)若点D是两条外角平分线的交点,填空:∠BDC= °.
(3)若点E是内角∠ABC、外角∠ACG的平分线的交点,试探索:∠BEC与∠BAC的数量关系,并说明理由.
(4)在问题(3)的条件下,当∠ACB等于 度时,CE∥AB?
32、△ABC中,∠C=70°,点D、E分别是△ABC边AC、BC上的两个定点,点P是平面内一动点,令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
初探:(1)如图1,若点P在线段AB上运动,
①当∠α=60°时,则∠1+∠2= °;
②∠α、∠1、∠2之间的关系为: .
再探:(2)若点P运动到边AB的延长线上,如图2,则∠α、∠1、∠2之间有何关系?并说明理由.
拓展:(3)请你试着给出一个点P的其他位置,在图3中补全图形,并写出此时∠α、∠1、∠2之间的关系: .
专题复习提升训练卷7.3三角形-20-21苏科版七年级数学下册(答案)
一、选择题
1、对图理解错误的是 ( C )
A.∠A,∠B,∠ACB是△ABC的内角 B.∠BCD是与∠ACB相邻的外角
C.∠BCD+∠A=180° D.△ABC的三条边分别是线段AB,BC,AC
2、如图,在△ABC中有四条线段DE,BE,EG,FG,其中有一条线段是△ABC的中线,则该线段是 ( B )
A.DE B.BE C.EG D.FG
3、若△ABC的一个外角为50°,则△ABC一定是 ( B )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.锐角三角形或钝角三角形
4、下列说法正确的是 ( D )
A.一个直角三角形一定不是等腰三角形 B.一个等腰三角形一定不是锐角三角形
C.一个钝角三角形一定不是等腰三角形 D.一个等边三角形一定不是钝角三角形
5、下列说法不正确的是 ( C )
A.三角形的中线在三角形的内部 B.三角形的角平分线在三角形的内部
C.三角形的高都在三角形的内部 D.三角形必有一条高在三角形的内部
6、如图,在△ABC中,∠1=∠2,G为AD的中点,延长BG交AC于点E,F为AB上的一点,CF⊥AD于点H.
下列说法正确的是 ( C )
A.AD是△ABE的角平分线 B.BE是△ABD中边AD上的中线
C.CH为△ACD中边AD上的高 D.AH为△ABC的角平分线
7、如图,在三角形ABC中,,,AD平分交BC于D,DE?AB交AC于E,
则的大小是( )
A.45° B.54° C.39° D.50°
解:∵,∴∠BAC=180°-
∵AD平分,∴∠BAD=∠BAC=39°
∵DE?AB,∴==,故选C.
8、如图,在△ABC中,∠BAC=60°,BD、CE分别平分∠ABC、∠ACB,BD、CE相交于点O,
则∠BOC的度数是( )
A.120° B.130° C.75° D.150°
解:∵∠BAC=60°,∴∠ABC+∠ACB=,
∵BD,CE分别平分∠ABC,∠ACB, ∴OBC=ABC,OCB=ACB,
∴OBC+OCB=(∠ABC+ACB)
∴∠BOC=180°-(∠ABC+∠ACB)=180°-×=120°.
故选:A.
9、如图,已知 AB//CD,则( A )
A.∠1=∠2+∠3 B.∠1=2∠2+∠3 C.∠1=2∠2-∠3 D.∠1=180°-∠2-∠3
10、如图,已知//b,那么下列式子中,结果等于180°的是 ( B )
A.+β+γ B.+β-γ C.-+β+γ D.-β+γ
11、小明把一副含45、30°角的直角三角板如图摆放,其中∠C=∠F=90°,∠A=45°,∠D =30°,
则∠α+∠β等于( B )
A.180° B.210° C.360° D.270°
12、如图,AB和CD相交于点O,∠A=∠C,则下列结论中不能完全确定正确的是( )
A.∠B=∠D B.∠1=∠A+∠D C.∠2>∠D D.∠C=∠D
解:∵∠A+∠AOD+∠D=180°,∠C+∠COB+∠B=180°,∠A=∠C,∠AOD=∠BOC,
∴∠B=∠D,
∵∠1=∠2=∠A+∠D,
∴∠2>∠D,
故选项A,B,C正确,
故选:D.
13、如图,在△ABC中,AD是高,AE、BF是两内角平分线,它们相交于点O,∠CAB=50°,∠C=60°,求∠DAE和∠BOA的度数之和为( )
A.115° B.120° C.125° D.130°
解:∵∠CAB=50°,∠C=60°∴∠ABC=180°﹣50°﹣60°=70°,
又∵AD是高,∴∠ADC=90°,∴∠DAC=180°﹣90°﹣∠C=30°,
∵AE、BF是角平分线,∴∠CBF=∠ABF=35°,∠EAF=25°,
∴∠DAE=∠DAC﹣∠EAF=5°,∠AFB=∠C+∠CBF=60°+35°=95°,
∴∠BOA=∠EAF+∠AFB=25°+95°=120°,
∴∠DAE+∠BOA=5°+120°=125°.故选:C.
14、如图,已知点E,D分别在△ABC边BA和CA的延长线上,CF和EF分别平分∠ACB和∠AED.如果∠B=70°,∠D=50°,则∠F的度数是( )
A.50° B.55° C.60° D.65°
解:如图,设AB交CF于点G,
∵CF、EF分别平分∠ACB和∠AED, ∴∠BCF=∠ACF,∠DEF=∠AEF,
∵∠BCF+∠B=∠AEF+∠F;∠BCF+∠ACF+∠B=∠DEF+∠AEF+∠D,
即2∠BCF+∠B=2∠AEF+∠D,
又∵∠B=70°,∠D=50°,
∴∠BCF+70°=∠AEF+∠F①,2∠BCF+70°=2∠AEF+50°②,
①×2﹣②得,70°=2∠F﹣50°,
解得∠F=60°.
故选:C.
二、填空题
15、如图,图中共有 个三角形,以AB为一边的三角形是 ,
其中∠BDC既是 的内角,又是 的外角.?
答案: 3 △ABC, △ABD △BCD △ABD
16、已知三角形的三边长a,b,c满足(a-b)2+=0,则该三角形按边分类是 等边 三角形.
17、已知三角形的三边长为3,6,a,则a的取值范围是 3
答案: △ABC,△ADC △ADE,△ACE,△ABE △ABD
19、如图,五角星五个角的和∠A+∠B+∠C+∠D+∠E=___180°_____
20、如图,已知∠1=20°,∠2=25°,∠A=35°,则∠BDC=__80°_____
21、如图所示的折线图形中,α+β= .
解:方法一:如图,连接BC.
在△EBC中,∠1+∠2=180°﹣∠E=140°,
在四边形ABCD中,∠A+∠ABC+∠BCD+∠D=360°,
∴70°+α+∠1+∠2+β+65°=360°,
∴α+β=360°﹣70°﹣65°﹣140°=85°,
方法二:∵α+70=40+?4,
β+65=40+?3
∴α+70+β+65=40+?4+40+?3
∴α+β=40+180-70-65=85°
故答案为85°.
22、如图,在△ABC中,∠B=47°,三角形的外角∠DAC和∠ACF的平分线交于点E,则∠AEC=__66.5°___
23、将两张三角形纸片如图摆放量得∠1+∠2+∠3+∠4=230°,则∠5= .
解:如图所示:∠1+∠2+∠6=180°,∠3+∠4+∠7=180°,
∵∠1+∠2+∠3+∠4=230°,∴∠1+∠2+∠6+∠3+∠4+∠7=360°,∴∠6+∠7=130°,
∴∠5=180°﹣(∠6+∠7)=50°. 故答案为:50°.
24、如图,在△ABC中,E是BC上的一点,EC=2BE,点D是AC的中点.设△ABC,△ADF,△BEF的面积分别为S△ABC,S△ADF,S△BEF,且S△ABC=12,则S△ADF-S△BEF=2 .
三、解答题
25、已知:如图, 画出△ABC中BC边上的高,AB边上的中线,∠ABC的平分线.
解: 如图所示.(1)过点A画AD⊥CB交CB的延长线于点D,则AD即为△ABC的BC边上的高.
(2)画AB边的中点F,连结CF,则CF即为AB边的中线.
(3)画BE平分∠ABC交AC于点E,则线段BE即为∠ABC的平分线.
26、已知一个等腰三角形的三边长分别为x,2x-4,5x-12,求其周长=_________
解:①当x=2x-4时,x=4,即三边长为4,4,8.此时不能构成三角形;
②当x=5x-12时,x=3,即三边长为3,2,3,其周长为8;
③当2x-4=5x-12时,x=,
即三边长为,,,不能构成三角形.
故三角形周长为8.
27、如图,AD是△ABC的中线,BE是△ABD的中线.
(1)作出△BDE中BD边上的高;
(2)若△ABC的面积为40,BD=5,求△BDE中BD边上的高.
解:(1)如图, EF为△BDE中BD边上的高
(2)因为AD是△ABC的中线,所以S△ABD=S△ABC.
同理,S△BDE=S△ABD, 所以S△BDE=S△ABC.
因为S△BDE=BD·EF,所以BD·EF=S△ABC.
又因为△ABC的面积为40,BD=5, 所以EF=4.
即△BDE中BD边上的高是4.
28、如图,在△ABC中,BE是AC边上的高,DE∥BC,∠ADE=45°,∠C=65°,求∠ABE的度数.
解:∵DE∥BC,∠ADE=45°,∴∠ABC=∠ADE=45°,
∵BE是AC边上的高,∴∠BEC=90°,
∵∠C=65°,∴∠EBC=90°﹣∠C=25°,
∴∠ABE=∠ABC﹣∠EBC=45°﹣25°=20°.
29、(1)如图1的图形我们把它称为“8字形”,则∠A、∠B、∠C、∠D之间的数量关系为 ;
(2)如图2,AP、CP分别平分∠BAD、∠BCD.
①图中有 个“8字形”;
②若∠B=36°,∠D=14°,求∠P的度数;
(3)如图3,CP、AG分别平分∠BCE、∠FAD,AG反向延长线交CP于点P,求∠P、∠B、∠D之间的数量关系.
【解析】(1)∵∠A+∠B+∠AOB=180°,∠C+∠D+∠COD=180°,
又∵∠AOB=∠COD,∴∠A+∠B=∠C+∠D, 故答案为:∠A+∠B=∠C+∠D.
(2)①图中,有6个“8字形”. 故答案为6.
②∵AP平分∠BAD,∴∠1=∠2, ∵PC平分∠BCD,∴∠3=∠4,
∵∠1+∠B=∠3+∠P①, ∠2+∠P=∠4+∠D②,
①﹣②得,2∠P=∠B+∠D=50°,∴∠P=25°.
(3)结论:2∠P=∠B+∠D.
理由:∵CP平分∠BCE,∴∠3=∠4,
∵AG平分∠DAF,∴∠1=∠2, ∵∠PAB=∠1,∴∠2=∠PAB,
∵∠P+∠PAB=∠B+∠4, ∴∠P+∠2=∠B+∠4 ③,
∵∠P+∠PAD=∠D+∠PCD,∴∠P+(180°﹣∠2)=∠D+(180°﹣∠3)④,
③+④得,2∠P=∠B+∠D.
30、如图,若P点是△ABC三个内角的角平分线的交点.
(1)∠PBC= ∠ABC,∠PCB= ∠ACB;
(2)用∠BAC来表示∠BPC;
(3)猜想:∠CPA=90°+ ,∠APB=90°+ .
解:(1)∵P点是△ABC三个内角的角平分线的交点,
∴∠PBC=∠ABC,∠PCB=∠ACB,
故答案为:,;
(2)∵∠PBC=∠ABC,∠PCB=∠ACB,
∴∠BPC=180°﹣(∠PBC+∠PCB)=180°﹣(∠ABC+∠ACB)
=180°﹣(180°﹣∠BAC)=180°﹣90°+∠BAC=90°+∠BAC;
(3)猜想:∠CPA=90°+∠ABC,∠APB=90°+∠ACB;
理由如下:∵AP平分∠BAC,CP平分∠ACB
∴∠PAC=,∠ACP=
∴∠CPA=180°﹣(∠PAC+∠ACP)=180°﹣(∠BAC+∠ACB)
=180°﹣(1800﹣∠ABC)=180°﹣90°+∠ABC=90°+∠ABC;
同理可得:∠APB=90°+∠ACB.
故答案为:,∠ACB.
31、好学的小红在学完三角形的角平分线后,遇到下列4个问题,请你帮她解决.如图,在△ABC中,
∠BAC=48°,点I是两角∠ABC、∠ACB的平分线的交点.
(1)填空:∠BIC= °.
(2)若点D是两条外角平分线的交点,填空:∠BDC= °.
(3)若点E是内角∠ABC、外角∠ACG的平分线的交点,试探索:∠BEC与∠BAC的数量关系,并说明理由.
(4)在问题(3)的条件下,当∠ACB等于 度时,CE∥AB?
【解析】(1)∵∠A=48°,∴∠ABC+∠ACB=180°﹣48°=132°,
∵点I是两角∠ABC、∠ACB的平分线的交点,
∴∠IBC+∠ICB=(∠ABC+∠ACB)=66°,
∴∠BIC=180°﹣66°=114°.故答案为114.
(2)由题意:∠IBD=∠ICD=90°,∴∠BDC+∠BIC=180°,
∴∠BDC=66°.故答案为66.
(3)设∠ACE=∠ECG=x,∠ABI=∠IBC=y,
∴2x=2y+∠A①,
x=y+∠E②,
①÷2﹣②可得∠E=∠A.
(4)∵CE∥AB,∴∠ECA=∠A=48°,
∴∠ECG=∠ECA=∠ABC=48°,
∴∠ACB=180°﹣48°﹣48°=84°, 故答案为84.
32、△ABC中,∠C=70°,点D、E分别是△ABC边AC、BC上的两个定点,点P是平面内一动点,令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
初探:(1)如图1,若点P在线段AB上运动,
①当∠α=60°时,则∠1+∠2= °;
②∠α、∠1、∠2之间的关系为: .
再探:(2)若点P运动到边AB的延长线上,如图2,则∠α、∠1、∠2之间有何关系?并说明理由.
拓展:(3)请你试着给出一个点P的其他位置,在图3中补全图形,并写出此时∠α、∠1、∠2之间的关系: .
【解析】(1)①如图1中,连接PC.∵∠1=∠DCP+∠DPC,∠2=∠ECP+∠CPE,
∴∠1+∠2=∠DCP+∠DCP+∠ECP+∠EPC=∠ACB+∠DPE=∠ACB+∠α,
∵∠ACB=70°,∠α=60°,∴∠1+∠2=60°+70°=130°.
②由①可知,∠1+∠2=∠ACB+∠α=70°+∠α,
故答案为130,70°+∠α.
(2)结论:∠1=70°+∠2+∠α.
理由:如图2中,∵∠1=∠C+∠CFD,∠CFD=∠2+∠α,∴∠1=70°+∠2+∠α.
(3)结论:∠1+∠2=430°﹣∠α.
理由:如图3中,∵∠1=∠DCP+∠DPC,∠2=∠ECP+∠CPE,
∴∠1+∠2=∠DCP+∠DPC+∠ECP+∠EPC=∠ACB+360°﹣∠DPE=70°+360°﹣∠α,
∴∠1+∠2=430°﹣∠α.
故答案为∠1+∠2=430°﹣∠α.
同课章节目录
- 第7章 平面图形的认识(二)
- 7.1 探索直线平行的条件
- 7.2 探索平行线的性质
- 7.3 图形的平移
- 7.4 认识三角形
- 7.5 多边形的内角和与外角和
- 第8章 幂的运算
- 8.1 同底数幂的乘法
- 8.2 幂的乘方与积的乘方
- 8.3 同底数幂的除法
- 第9章 整式乘法与因式分解
- 9.1 单项式乘单项式
- 9.2 单项式乘多项式
- 9.3 多项式乘多项式
- 9.4 乘法公式
- 9.5 多项式的因式分解
- 第10章 二元一次方程组
- 10.1 二元一次方程
- 10.2 二元一次方程组
- 10.3 解二元一次方程组
- 10.4 三元一次方程组
- 10.5 用二元一次方程解决问题
- 第11章 一元一次不等式
- 11.1 生活中的不等式
- 11.2 不等式的解集
- 11.3 不等式的性质
- 11.4 解一元一次不等式
- 11.5 用一元一次不等式解决问题
- 11.6 一元一次不等式组
- 第12章 证明
- 12.1 定义与命题
- 12.2 证明
- 12.3 互逆命题
