5.2 探索轴对称的性质课件(28张)
文档属性
| 名称 | 5.2 探索轴对称的性质课件(28张) |  | |
| 格式 | pptx | ||
| 文件大小 | 385.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 13:30:34 | ||
图片预览





文档简介
5.2探索轴对称的性质
进一步复习生活中的轴对称现象,探索并掌握轴对称的性质.
01
02
03
学习目标
会利用轴对称的性质作对称点、对称图形、对称轴等.
经历丰富材料的学习过程,提高对图形的观察、分析、判断、归纳等能力.
掌握轴对称的性质.
会利用轴对称的性质作对称点、对称图形、对称轴等.
重点:
难点:
学习重难点
情景导入
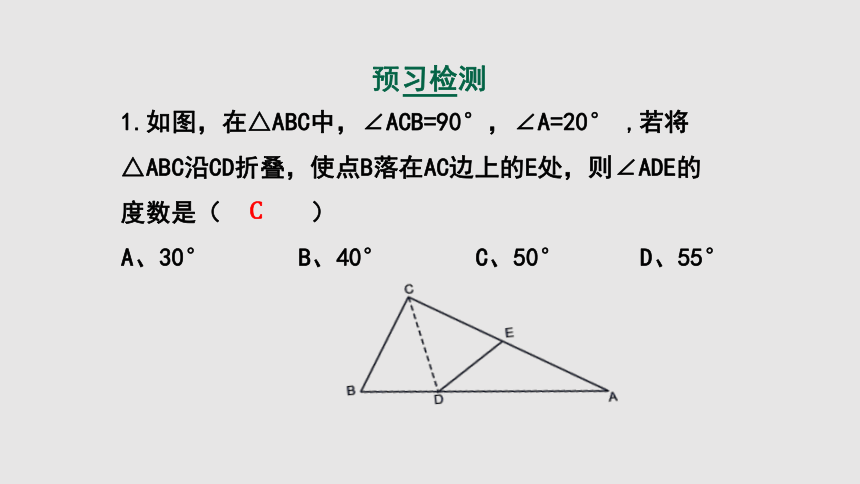
预习检测
1.如图,在△ABC中,∠ACB=90°,∠A=20° ,若将△ABC沿CD折叠,使点B落在AC边上的E处,则∠ADE的度数是( )
C
A、30° B、40° C、50° D、55°
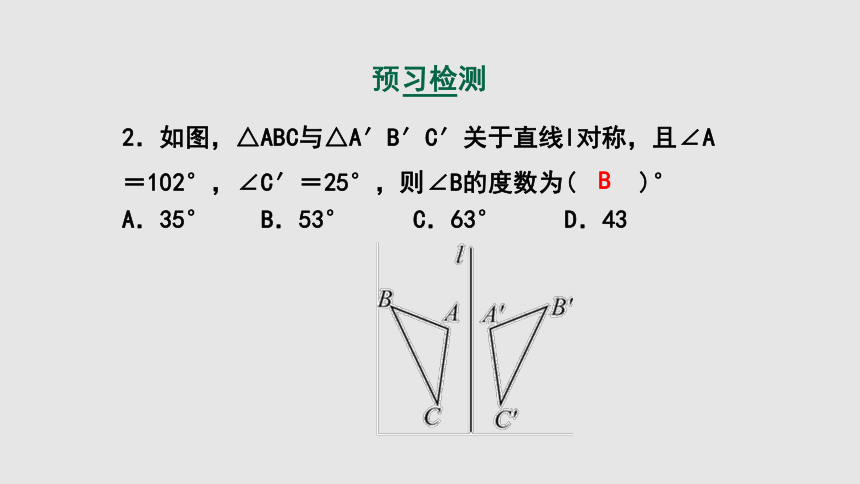
2.如图,△ABC与△A′B′C′关于直线l对称,且∠A=102°,∠C′=25°,则∠B的度数为( )°
B
A.35° B.53° C.63° D.43
预习检测
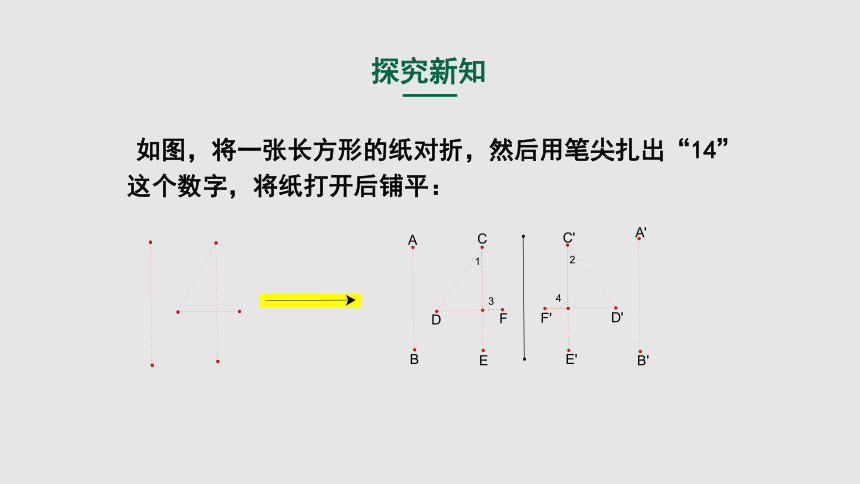
探究新知
如图,将一张长方形的纸对折,然后用笔尖扎出“14”这个数字,将纸打开后铺平:
探究新知
(1)两个“14”有什么关系?
打开
(2)设折痕所在直线为l,连接点E和E′的线段和l有什么关系?连接点F和F′的线段呢?
被直线l垂直平分.
成轴对称图形.
(3)线段AB与A′B′,CD与C′D′有什么关系?
(4)∠1与∠2有什么关系?∠3与∠4呢?
AB = A′B′,CD = C′D′.
∠1=∠2,∠3=∠4.
打开
探究新知
做一做
右图是一个轴对称图形:
(1)找出它的对称轴.
(2)连接点A与点A1的线段与对称轴有什么关系?连接点B与点B1的线段呢?
B
C
D
D1
C1
B1
3
4
1
2
都被对称轴垂直平分.
(3)线段AD与线段A1D1有什么关系?线段BC与B1C1呢?为什么?
AD=A1D1,BC=B1C1.
(4)∠1与∠2有什么关系?∠3与∠4呢?说说你的理由?
∠1=∠2,∠3=∠4.
思考:综合以上问题,你能得到什么结论?
B
C
D
D1
C1
B1
3
4
1
2
做一做
归纳总结
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.
轴对称的基本性质:
典例精析
【例1】 下列“禁止行人通行,注意危险,禁止非机动车通行,限速60”四个交通标志图中,为轴对称图形的是( )
B
探究新知
【例2】将一张正方形纸片按如图①,图②所示的方向对折,然后沿图③中的虚线剪裁得到图④,将图④的纸片展开铺平,再得到的图案是( )
图①
图②
图③
图④
A
B
C
D
B
变式训练
下面是四位同学作△ABC关于直线MN的轴对称图形,其中正确的是( )
B
﹒
探究新知
问题1:如何画一个点的轴对称图形?
画出点A关于直线l的对称点A′.
﹒
A
A′
O
作法:
(1)过点A作l的垂线,垂足为点O.
(2)在垂线上截取OA′=OA.
点A′就是点A关于直线l的对称点.
????
?
探究新知
如何画一条线段的对称图形?
已知线段AB,画出AB关于直线l的对称线段.
A
B
(图1)
(图2)
(图3)
A
B
l
l
A
B
l
A ′
A ′
B ′
(B ′)
想一想
如果有一个图形和一条直线,如何画出与这个图形关于这条直线对称的图形呢?
如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
A
B
C
探究新知
作法:(1)过点A画直线l的垂线,垂足为点O,在垂线上截取OA′=OA,A′就是点A关于直线l的对称点.
(3)连接A′B′,B′C′,C′A′,得到△ A′B′C′即为所求.
(2)同理,分别画出点B,C关于直线l的对称点B′,C′ .
A
B
C
A′
B′
C′
O
归纳总结
作轴对称图形的方法
几何图形都可以看作由点组成.对于某些图形,只要作出图形中一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
想一想
下图是一个图案的一半,其中的虚线是这个图案的对称轴,画出这个图案的另一半.
课堂练习
B
1.作已知点关于某直线的对称点的第一步是( )
A.过已知点作一条直线与已知直线相交
B.过已知点作一条直线与已知直线垂直
C.过已知点作一条直线与已知直线平行
D.不确定
课堂练习
2.如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为( )
A.10° B.20° C.30° D.40°
A
A
?
B
?
C
?
D
?
B’
?
课堂练习
3.如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若得∠AOB′=70°,则∠B′OG的度数为________.
55°
课堂练习
4.如图,把下列图形补成关于直线l的对称图形.
????
?
????
?
课堂练习
5.如图给出了一个图案的一半,虚线 l 是这个图案的对称轴.整个图案是个什么形状?请准确地画出它的另一半.
B
A
C
D
E
F
G
H
l
总结
轴对称的性质
性质
作图方法
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.
(1)找特征点;
(2)作垂线;
(3)截取等长;
(4)依次连线.
谢谢观看!
进一步复习生活中的轴对称现象,探索并掌握轴对称的性质.
01
02
03
学习目标
会利用轴对称的性质作对称点、对称图形、对称轴等.
经历丰富材料的学习过程,提高对图形的观察、分析、判断、归纳等能力.
掌握轴对称的性质.
会利用轴对称的性质作对称点、对称图形、对称轴等.
重点:
难点:
学习重难点
情景导入
预习检测
1.如图,在△ABC中,∠ACB=90°,∠A=20° ,若将△ABC沿CD折叠,使点B落在AC边上的E处,则∠ADE的度数是( )
C
A、30° B、40° C、50° D、55°
2.如图,△ABC与△A′B′C′关于直线l对称,且∠A=102°,∠C′=25°,则∠B的度数为( )°
B
A.35° B.53° C.63° D.43
预习检测
探究新知
如图,将一张长方形的纸对折,然后用笔尖扎出“14”这个数字,将纸打开后铺平:
探究新知
(1)两个“14”有什么关系?
打开
(2)设折痕所在直线为l,连接点E和E′的线段和l有什么关系?连接点F和F′的线段呢?
被直线l垂直平分.
成轴对称图形.
(3)线段AB与A′B′,CD与C′D′有什么关系?
(4)∠1与∠2有什么关系?∠3与∠4呢?
AB = A′B′,CD = C′D′.
∠1=∠2,∠3=∠4.
打开
探究新知
做一做
右图是一个轴对称图形:
(1)找出它的对称轴.
(2)连接点A与点A1的线段与对称轴有什么关系?连接点B与点B1的线段呢?
B
C
D
D1
C1
B1
3
4
1
2
都被对称轴垂直平分.
(3)线段AD与线段A1D1有什么关系?线段BC与B1C1呢?为什么?
AD=A1D1,BC=B1C1.
(4)∠1与∠2有什么关系?∠3与∠4呢?说说你的理由?
∠1=∠2,∠3=∠4.
思考:综合以上问题,你能得到什么结论?
B
C
D
D1
C1
B1
3
4
1
2
做一做
归纳总结
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.
轴对称的基本性质:
典例精析
【例1】 下列“禁止行人通行,注意危险,禁止非机动车通行,限速60”四个交通标志图中,为轴对称图形的是( )
B
探究新知
【例2】将一张正方形纸片按如图①,图②所示的方向对折,然后沿图③中的虚线剪裁得到图④,将图④的纸片展开铺平,再得到的图案是( )
图①
图②
图③
图④
A
B
C
D
B
变式训练
下面是四位同学作△ABC关于直线MN的轴对称图形,其中正确的是( )
B
﹒
探究新知
问题1:如何画一个点的轴对称图形?
画出点A关于直线l的对称点A′.
﹒
A
A′
O
作法:
(1)过点A作l的垂线,垂足为点O.
(2)在垂线上截取OA′=OA.
点A′就是点A关于直线l的对称点.
????
?
探究新知
如何画一条线段的对称图形?
已知线段AB,画出AB关于直线l的对称线段.
A
B
(图1)
(图2)
(图3)
A
B
l
l
A
B
l
A ′
A ′
B ′
(B ′)
想一想
如果有一个图形和一条直线,如何画出与这个图形关于这条直线对称的图形呢?
如图,已知△ABC和直线l,作出与△ABC关于直线l对称的图形.
A
B
C
探究新知
作法:(1)过点A画直线l的垂线,垂足为点O,在垂线上截取OA′=OA,A′就是点A关于直线l的对称点.
(3)连接A′B′,B′C′,C′A′,得到△ A′B′C′即为所求.
(2)同理,分别画出点B,C关于直线l的对称点B′,C′ .
A
B
C
A′
B′
C′
O
归纳总结
作轴对称图形的方法
几何图形都可以看作由点组成.对于某些图形,只要作出图形中一些特殊点(如线段端点)的对称点,连接这些对称点,就可以得到原图形的轴对称图形.
想一想
下图是一个图案的一半,其中的虚线是这个图案的对称轴,画出这个图案的另一半.
课堂练习
B
1.作已知点关于某直线的对称点的第一步是( )
A.过已知点作一条直线与已知直线相交
B.过已知点作一条直线与已知直线垂直
C.过已知点作一条直线与已知直线平行
D.不确定
课堂练习
2.如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB'关于直线AD对称,点B的对称点是点B',则∠CAB'的度数为( )
A.10° B.20° C.30° D.40°
A
A
?
B
?
C
?
D
?
B’
?
课堂练习
3.如图,把一张长方形的纸按图那样折叠后,B、D两点落在B′、D′点处,若得∠AOB′=70°,则∠B′OG的度数为________.
55°
课堂练习
4.如图,把下列图形补成关于直线l的对称图形.
????
?
????
?
课堂练习
5.如图给出了一个图案的一半,虚线 l 是这个图案的对称轴.整个图案是个什么形状?请准确地画出它的另一半.
B
A
C
D
E
F
G
H
l
总结
轴对称的性质
性质
作图方法
在轴对称图形或两个成轴对称的图形中,对应点所连的线段被对称轴垂直平分,对应线段相等,对应角相等.
(1)找特征点;
(2)作垂线;
(3)截取等长;
(4)依次连线.
谢谢观看!
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
