4.3.1探索全等三角形的条件课件(19张)
文档属性
| 名称 | 4.3.1探索全等三角形的条件课件(19张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 371.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 00:00:00 | ||
图片预览




文档简介
探索三角形全等的条件(1)
1、探索“边边边”定理证明两个三角形全等;
2、掌握三角形的稳定性。
学习目标
掌握“边边边”定理证明两个三角形全等;
掌握三角形的稳定性。
重点
难点
熟练运用“边边边”定理证明两个三角形全等。
学习重点和难点
我们知道:如果两个三角形全等,那么他们的对应边相等,对应角相等。
反过来,当两个三角形具备什么条件,即它们有多少组边或角分别相等时就全等?
思考
对应边相等,对应角相等.
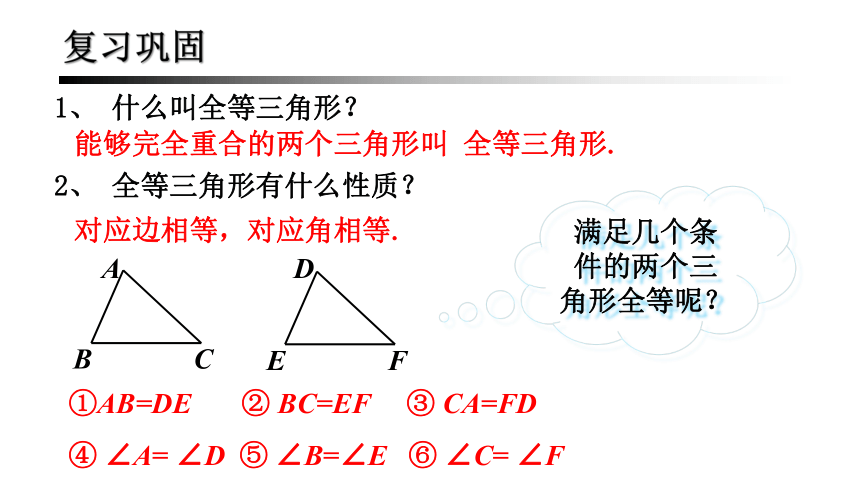
1、 什么叫全等三角形?
能够完全重合的两个三角形叫 全等三角形.
2、 全等三角形有什么性质?
①AB=DE ② BC=EF ③ CA=FD
④ ∠A= ∠D ⑤ ∠B=∠E ⑥ ∠C= ∠F
A
B
C
D
E
F
满足几个条件的两个三角形全等呢?
复习巩固
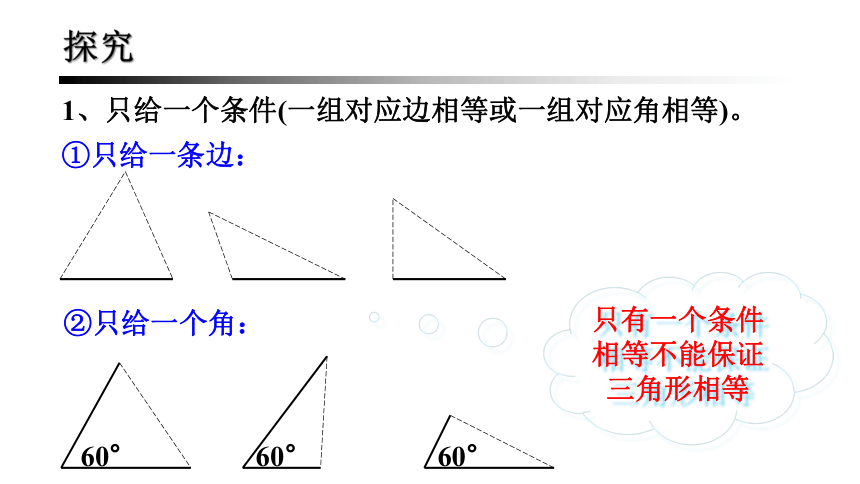
1、只给一个条件(一组对应边相等或一组对应角相等)。
①只给一条边:
②只给一个角:
60°
60°
60°
只有一个条件相等不能保证三角形相等
探究
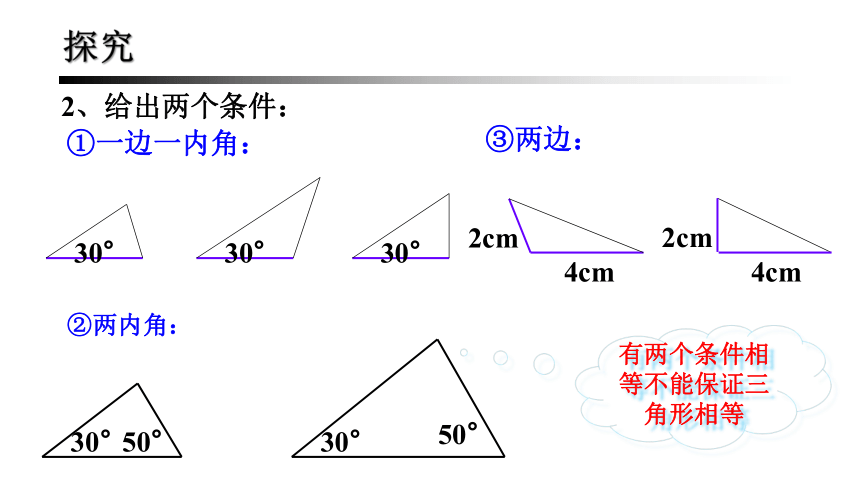
2、给出两个条件:
①一边一内角:
30°
30°
30°
②两内角:
30°
30°
50°
50°
③两边:
2cm
4cm
2cm
4cm
有两个条件相等不能保证三角形相等
探究
如果给出三个条件画三角形,你能说出有哪几种可能的情况吗?
1.三个角
2.三条边
3.两边一角
4.两角一边
那么我就开始探究一下如果给出这些条件,能否画出唯一三角形。
思考
给出三个角:
已知一个三角形的三个内角分别为40°,60°和80°,你能画出这个三角形吗?能画出多少个?形状大小都一样吗?
三个内角对应相等的两个三角形不一定全等
40°
60°
80°
60°
80°
40°
探究
给出三个边:
已知一个三角形的三条边分别为4cm ,5cm和7cm,你能画出这个三角形吗?你能画出几个?大小形状都一样吗?
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。
4cm
5cm
7cm
4cm
5cm
7cm
三边证全等
数学表达式:
在△ABC和△A'B'C'中
AB=A'B'
BC=B'C'
AC=A'C'
所以△ABC≌△ A'B'C' (SSS)
A
B
C
A'
B'
C'
三边证全等
如图所示,在△ABC和△EFD中,AD=FC,AB=FE,BC=ED.说明△ABC≌△FED.
证:因为AD=FC,所以AD+DC=FC+DC,
即AC=FD,在△ABC和△FED中,
∴△ABC≌△FED(SSS).
AC=FD,(已证)
AB=FE,(已知)
BC=ED,(已知)
【例1】
(1)取出三根硬纸条钉成一个三角形,你能拉动其中两边,使这个三角形的形状发生变化吗?
(2)取出四根硬纸条钉成一个四边形,拉动其中两边,这个四边形的形状改变了吗?钉成 一个五边形,又会怎么样?
(3)上面的现象说明了什么?
探究
三角形的框架,它的大小和形状是固定不变的,三角形的这个性质叫做三角形的稳定性。
你能举几个应用三角形稳定性的例子吗?
三角形的稳定性
观察
1.下列各组条件中能判定△ABC≌△DEF的是( )
(A)AB=DE,BC=EF
(B)∠A=∠D,∠C=∠F
(C)AB=DE,BC=EF,△ABC的周长等于△DEF的周长
(D)∠ A=∠D,∠B=∠ E, ∠C=∠F
C
练习
2.如图,△ABC中,AB=AC,EB=EC,则由“SSS”可以判定( )
(A)△ABD≌△ACD
(B)△ABE≌△ACE
(C)△BDE≌△CDE
(D)以上答案都不对
练习
B
3.如图,若AB=AC,AD=AE,则需要_______________ 条件就可根据“SSS”判断△ABE≌△ACD.
BE=CD或BD=CE
练习
1、三角形全等的条件:
三边对应相等的两个三角形全等(“边边边”或“SSS”)
2、三角形具有稳定性。
课堂总结
1、探索“边边边”定理证明两个三角形全等;
2、掌握三角形的稳定性。
学习目标
掌握“边边边”定理证明两个三角形全等;
掌握三角形的稳定性。
重点
难点
熟练运用“边边边”定理证明两个三角形全等。
学习重点和难点
我们知道:如果两个三角形全等,那么他们的对应边相等,对应角相等。
反过来,当两个三角形具备什么条件,即它们有多少组边或角分别相等时就全等?
思考
对应边相等,对应角相等.
1、 什么叫全等三角形?
能够完全重合的两个三角形叫 全等三角形.
2、 全等三角形有什么性质?
①AB=DE ② BC=EF ③ CA=FD
④ ∠A= ∠D ⑤ ∠B=∠E ⑥ ∠C= ∠F
A
B
C
D
E
F
满足几个条件的两个三角形全等呢?
复习巩固
1、只给一个条件(一组对应边相等或一组对应角相等)。
①只给一条边:
②只给一个角:
60°
60°
60°
只有一个条件相等不能保证三角形相等
探究
2、给出两个条件:
①一边一内角:
30°
30°
30°
②两内角:
30°
30°
50°
50°
③两边:
2cm
4cm
2cm
4cm
有两个条件相等不能保证三角形相等
探究
如果给出三个条件画三角形,你能说出有哪几种可能的情况吗?
1.三个角
2.三条边
3.两边一角
4.两角一边
那么我就开始探究一下如果给出这些条件,能否画出唯一三角形。
思考
给出三个角:
已知一个三角形的三个内角分别为40°,60°和80°,你能画出这个三角形吗?能画出多少个?形状大小都一样吗?
三个内角对应相等的两个三角形不一定全等
40°
60°
80°
60°
80°
40°
探究
给出三个边:
已知一个三角形的三条边分别为4cm ,5cm和7cm,你能画出这个三角形吗?你能画出几个?大小形状都一样吗?
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。
4cm
5cm
7cm
4cm
5cm
7cm
三边证全等
数学表达式:
在△ABC和△A'B'C'中
AB=A'B'
BC=B'C'
AC=A'C'
所以△ABC≌△ A'B'C' (SSS)
A
B
C
A'
B'
C'
三边证全等
如图所示,在△ABC和△EFD中,AD=FC,AB=FE,BC=ED.说明△ABC≌△FED.
证:因为AD=FC,所以AD+DC=FC+DC,
即AC=FD,在△ABC和△FED中,
∴△ABC≌△FED(SSS).
AC=FD,(已证)
AB=FE,(已知)
BC=ED,(已知)
【例1】
(1)取出三根硬纸条钉成一个三角形,你能拉动其中两边,使这个三角形的形状发生变化吗?
(2)取出四根硬纸条钉成一个四边形,拉动其中两边,这个四边形的形状改变了吗?钉成 一个五边形,又会怎么样?
(3)上面的现象说明了什么?
探究
三角形的框架,它的大小和形状是固定不变的,三角形的这个性质叫做三角形的稳定性。
你能举几个应用三角形稳定性的例子吗?
三角形的稳定性
观察
1.下列各组条件中能判定△ABC≌△DEF的是( )
(A)AB=DE,BC=EF
(B)∠A=∠D,∠C=∠F
(C)AB=DE,BC=EF,△ABC的周长等于△DEF的周长
(D)∠ A=∠D,∠B=∠ E, ∠C=∠F
C
练习
2.如图,△ABC中,AB=AC,EB=EC,则由“SSS”可以判定( )
(A)△ABD≌△ACD
(B)△ABE≌△ACE
(C)△BDE≌△CDE
(D)以上答案都不对
练习
B
3.如图,若AB=AC,AD=AE,则需要_______________ 条件就可根据“SSS”判断△ABE≌△ACD.
BE=CD或BD=CE
练习
1、三角形全等的条件:
三边对应相等的两个三角形全等(“边边边”或“SSS”)
2、三角形具有稳定性。
课堂总结
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
