4.3.3探索全等三角形的条件课件(15张)
文档属性
| 名称 | 4.3.3探索全等三角形的条件课件(15张) |  | |
| 格式 | pptx | ||
| 文件大小 | 136.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 13:43:57 | ||
图片预览





文档简介
探索三角形全等的条件(3)
1、探索三角形全等的条件 “边角边”.
2、熟练运用 “边角边”的内容,解决简单的证明问题.
学习目标
理解判定三角形全等的 “SAS”的条件。
重点
难点
运用判定三角形全等的 “SAS”的条件。
学习重点和难点
已知一个三角形的两条边和一个角,那么这两条边与这一个角的位置关系有几种可能的情况?
(1)两边及夹角
思考
(2)两边及其一边的对角
两边和它们的夹角对应相等的两个三角形全等,简写为“边角边”或“SAS”。
结论:
与同桌画出的三角形完全一样吗?
探究
三角形两边分别为2.5cm,3.5cm,它们所夹的角为40°,你能画出这个三角形吗?
(1)两边及夹角:
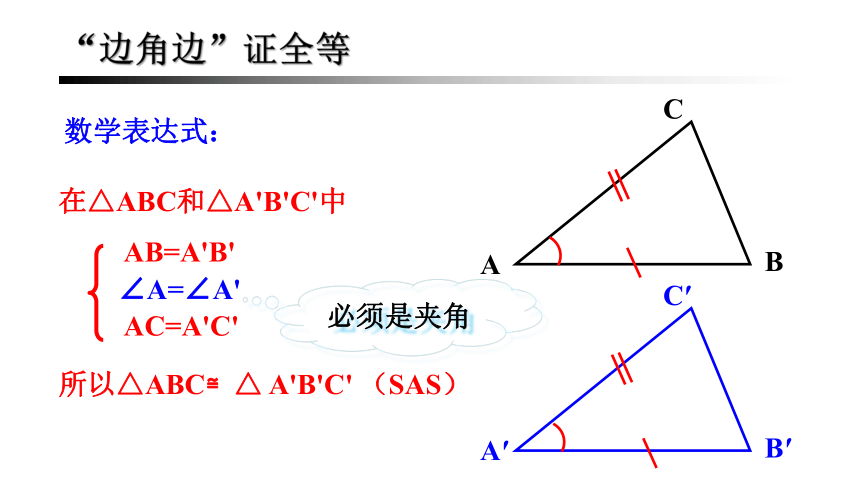
∠A=∠A'
AC=A'C'
AB=A'B'
所以△ABC≌△ A'B'C' (SAS)
在△ABC和△A'B'C'中
A
B
C
A′
B′
C′
“边角边”证全等
数学表达式:
必须是夹角
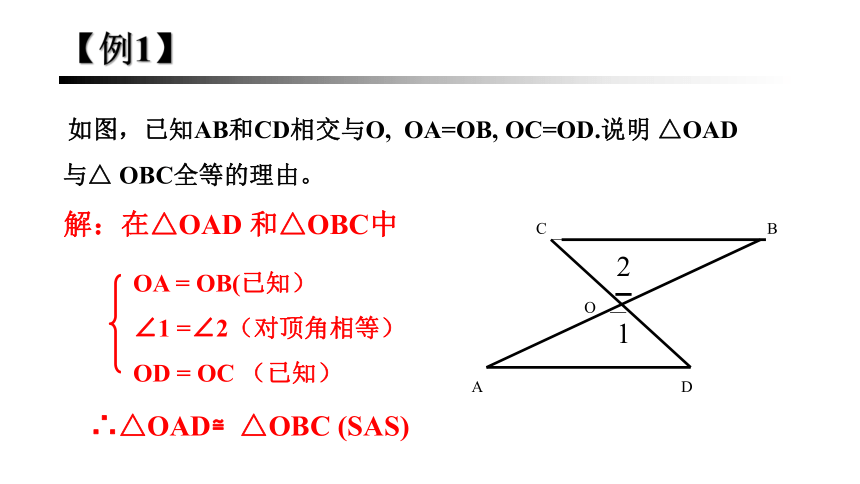
如图,已知AB和CD相交与O, OA=OB, OC=OD.说明 △OAD与△ OBC全等的理由。
C
B
A
D
O
2
1
解:在△OAD 和△OBC中
OA = OB(已知)
∠1 =∠2(对顶角相等)
OD = OC (已知)
∴△OAD≌△OBC (SAS)
【例1】
练习
已知:如图, AB=CB ,∠ABD= ∠CBD ,
△ABD和△CBD 全等吗?
A
B
C
D
在△ ABD 和△ CBD中
AB=CB
∠ABD= ∠CBD
BD=BD
∴△ ABD ≌△ CBD (SAS )
证明:
练习
在△ABC中,AB=AC,AD是∠BAC的角平分线。
那么BD与CD相等吗?为什么?
D
C
B
A
解:相等。
∵AD是∠BAC的角平分线
∴∠BAD=∠CAD
在△ABD和△ACD中
AB=AC
∠BAD=∠CAD
AD=AD
∴△ABD≌△ACD(SAS)∴BD=CD
两边及其一边所对的角对应相等,两个三角形不一定全等。
结论:
现在与同桌画出的三角形完全一样吗?
探究
(2)两边及其中一边的对角:
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40°,情况又怎样?
练习
如图,已知AB=AC,AD=AE,∠1=∠2.试说明:△ABD≌△ACE.
解:因为∠1=∠2,
所以∠1+∠EAB=∠2+∠EAB,
即∠BAD=∠CAE.
在△ABD和△ ACE中
所以△ABD≌△ACE(SAS).
AB=AC
∠BAD=∠CAE
AD=AE
练习
点M是等腰梯形ABCD底边AB的中点,求证△AMD≌△BMC.
证明:∵点M是等腰梯形ABCD底边AB的中点
∴AD=BC,∠A=∠B
AM=BM
在△ADM和△BCM中
∴△AMD≌△BMC (SAS)
AD=BC
∠A=∠B
AM=BM
练习
如图,已知点E,A,C在同一条直线上,AB∥CD,AB=CE,AC=CD.试说明:BC=ED.
证:因为AB∥CD,
所以∠BAC=∠ECD.
在△ABC和△CED中,
所以△ABC≌△CED(SAS),
所以BC=ED.
AB=CE
∠BAC=∠ECD
AC=CD
课堂总结
本节课学习了哪种判断全等三角形的方法?
用此方法判定时,需要注意什么?
再 见
1、探索三角形全等的条件 “边角边”.
2、熟练运用 “边角边”的内容,解决简单的证明问题.
学习目标
理解判定三角形全等的 “SAS”的条件。
重点
难点
运用判定三角形全等的 “SAS”的条件。
学习重点和难点
已知一个三角形的两条边和一个角,那么这两条边与这一个角的位置关系有几种可能的情况?
(1)两边及夹角
思考
(2)两边及其一边的对角
两边和它们的夹角对应相等的两个三角形全等,简写为“边角边”或“SAS”。
结论:
与同桌画出的三角形完全一样吗?
探究
三角形两边分别为2.5cm,3.5cm,它们所夹的角为40°,你能画出这个三角形吗?
(1)两边及夹角:
∠A=∠A'
AC=A'C'
AB=A'B'
所以△ABC≌△ A'B'C' (SAS)
在△ABC和△A'B'C'中
A
B
C
A′
B′
C′
“边角边”证全等
数学表达式:
必须是夹角
如图,已知AB和CD相交与O, OA=OB, OC=OD.说明 △OAD与△ OBC全等的理由。
C
B
A
D
O
2
1
解:在△OAD 和△OBC中
OA = OB(已知)
∠1 =∠2(对顶角相等)
OD = OC (已知)
∴△OAD≌△OBC (SAS)
【例1】
练习
已知:如图, AB=CB ,∠ABD= ∠CBD ,
△ABD和△CBD 全等吗?
A
B
C
D
在△ ABD 和△ CBD中
AB=CB
∠ABD= ∠CBD
BD=BD
∴△ ABD ≌△ CBD (SAS )
证明:
练习
在△ABC中,AB=AC,AD是∠BAC的角平分线。
那么BD与CD相等吗?为什么?
D
C
B
A
解:相等。
∵AD是∠BAC的角平分线
∴∠BAD=∠CAD
在△ABD和△ACD中
AB=AC
∠BAD=∠CAD
AD=AD
∴△ABD≌△ACD(SAS)∴BD=CD
两边及其一边所对的角对应相等,两个三角形不一定全等。
结论:
现在与同桌画出的三角形完全一样吗?
探究
(2)两边及其中一边的对角:
以2.5cm,3.5cm为三角形的两边,长度为2.5cm的边所对的角为40°,情况又怎样?
练习
如图,已知AB=AC,AD=AE,∠1=∠2.试说明:△ABD≌△ACE.
解:因为∠1=∠2,
所以∠1+∠EAB=∠2+∠EAB,
即∠BAD=∠CAE.
在△ABD和△ ACE中
所以△ABD≌△ACE(SAS).
AB=AC
∠BAD=∠CAE
AD=AE
练习
点M是等腰梯形ABCD底边AB的中点,求证△AMD≌△BMC.
证明:∵点M是等腰梯形ABCD底边AB的中点
∴AD=BC,∠A=∠B
AM=BM
在△ADM和△BCM中
∴△AMD≌△BMC (SAS)
AD=BC
∠A=∠B
AM=BM
练习
如图,已知点E,A,C在同一条直线上,AB∥CD,AB=CE,AC=CD.试说明:BC=ED.
证:因为AB∥CD,
所以∠BAC=∠ECD.
在△ABC和△CED中,
所以△ABC≌△CED(SAS),
所以BC=ED.
AB=CE
∠BAC=∠ECD
AC=CD
课堂总结
本节课学习了哪种判断全等三角形的方法?
用此方法判定时,需要注意什么?
再 见
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
