六年级下册数学教案 3.1 解决问题的策略 转化苏教版
文档属性
| 名称 | 六年级下册数学教案 3.1 解决问题的策略 转化苏教版 |  | |
| 格式 | doc | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 08:39:17 | ||
图片预览




文档简介
《解决问题的策略——转化》教学设计
【教学目标】
1.让学生经历回顾与探索运用转化策略解决问题的过程,初步感受转化策略的价值。
2.使学生初步学会运用转化的策略分析问题,并能根据问题的特点确定具体的转化方法,从而有效地解决问题。
3.使学生进一步积累运用转化策略解决问题的经验,增强解决问题的策略意识,获得成功的体验。
【教学重点】 感受“转化”策略的价值,会用“转化”的策略解决问题。
【教学难点】 会用“转化”的策略解决问题。
【教学过程】
课前交流,孕伏转化策略:
教师:同学们,大家好,很高兴再次能和大家再一起学习,为了缓和紧张的气氛,我给大家讲个小故事吧!(学生拭目以待)
教师:播放PPT,用优美的语言和动作来诠释故事内容。
教师:好的故事总能给人以启迪,从这个故事中,你受到了哪些启发呢?学生自由交流感受,教师适时小结:儿子能将复杂的事情与简单的事情相转化,从而巧妙的解决了问题,真是了不起,相信同学们也会有不俗的表现。
一、情境出示,合作探究
1、巧设例题,感知“转化”。
数学与生活息息相关,为了优化教学过程,我创造性地使用了教材,创设了我去喷绘版面,要按照面积收费,从而对面积的大小产生争议这一生活中的问题情境,引出例题1。(点课件)
先让学生猜测谁的面积大,再组织学生小组讨论、验证自己的猜测,我根据学生的汇报利用Powerpoint课件,形象直观的演示转化过程。
学生汇报预设:
师:有答案了吗?哪个图形的面积大?谁来说说。
生1:第一个图形的面积大。
生2:第二个图形的面积大。
生3:两个图形的面积相等。
师:你是如何比较出来的?
生:(边演示边说)我们把这块切开放到这块,都变成了长5个格、宽4个格的长方形。
教师注意引导学生说出方法,如何平移、旋转的?
师:听明白了吗?想的巧妙,讲的也非常清楚。谁再来说一说?)
师:原来的图形不规则,不容易比较大小。同学们都是利用了图形凹凸的特点想到了这个好办法,非常善于观察、思考。下面我们再来清晰的演示一下这个变化过程。请看,(课件演示)平移,旋转,瞧,哪个图形面积大?(相等)真是一目了然,原来的两个不规则图形通过平移、旋转都变成了规则的的图形。 (板书:不规则图形 规则图形)你们知道吗,这是一种解决问题的策略,这种策略就叫转化(板书课题)
进一步引导:
师:这样转化,什么变了?什么没变?
生:周长变了,面积没变。
师:还有什么变了?(形状变了。)
师:你抓住了问题的关键,的确,这样转化,形状变了,面积却没变。(板书:形变积不变)
二、唤醒记忆,回顾转化策略
1.图形面积、体积方面的应用。
师:同学们,其实,在以前的学习中,我们就经常用到转化的策略解决问题,比如说一些图形的面积公式、体积公式的推导,就常常用到转化的策略,你们能想起来吗?自己先想一想,然后跟小组的伙伴交流交流。
小组汇报过程预设:
生:在学习图形的面积时,三角形的面积。把两个完全一样的三角形拼成一个平行四边形。
师:这是把一个三角形的面积转化成了平行四边形面积的一半。没错,这就是转化。
师:还有谁想说?
生:把两个完全一样的梯形拼成一个平行四边形。
师:这是把什么转化成什么?
生:梯形转化成平行四边形
师:准确的说,这是把梯形转化成平行四边形面积的(一半)这也是转化。还有吗?
生:把平行四边行转化成长方形。
生:圆也是把圆分成若干个小扇形,然后再拼成一个近似的长方形。
生:圆柱是把圆柱转化成长方体。
师:这也是用转化解决的新问题。
课件出示:
平行四边形的面积公式推导 三角形的面积公式推导
梯形的面积公式推导 圆的面积公式推导
圆柱的体积公式推导 圆锥的体积公式推导
师:大家来看,我们曾经用转化的策略解决了这么多新问题。选一个你最喜欢的、或者感觉有困难的,二人小组互相说一说。
2.数与计算方面的应用。
师:从某种意义上来说,学习数学就是不断学会转化的过程。不仅在图形的世界里常常应用转化的策略解决问题,而且,在看似简单的计算中也蕴含着转化,回忆一下,在学习数与计算时,哪些地方用到了转化的策略呢?
小组汇报过程预设:
生:小数乘法是转化为整数乘法,分数除法是转化为分数乘法来进行计算的……
(出示课件)
师:请看,这儿有一组题,可以动笔算一算,体会体会转化的作用,看看从中你又能发现什么,然后在小组内交流交流。
(学生活动是巡视关注:是否会表达。)
生:计算+,是把异分母分数转化成同分母分数。
师:说的真好,谁能像他这样,举个例子也说说自己的发现。
生:2.5×0.4是把小数乘法转化整数乘法。
… … … …
师:说得真完整。
师:很高兴你和大家分享你的发现,重复的我们就不说了,谁还有不同的发现?
师:在计算这几个题的时候,我们都用到了转化的策略,转化前和转化后有什么关系?
生:得数相同。
师:你可真了不起,一下就抓住了转化的实质,转化前和转化后结果不变。(板书:得数相等)
三、实践应用,体验转化策略
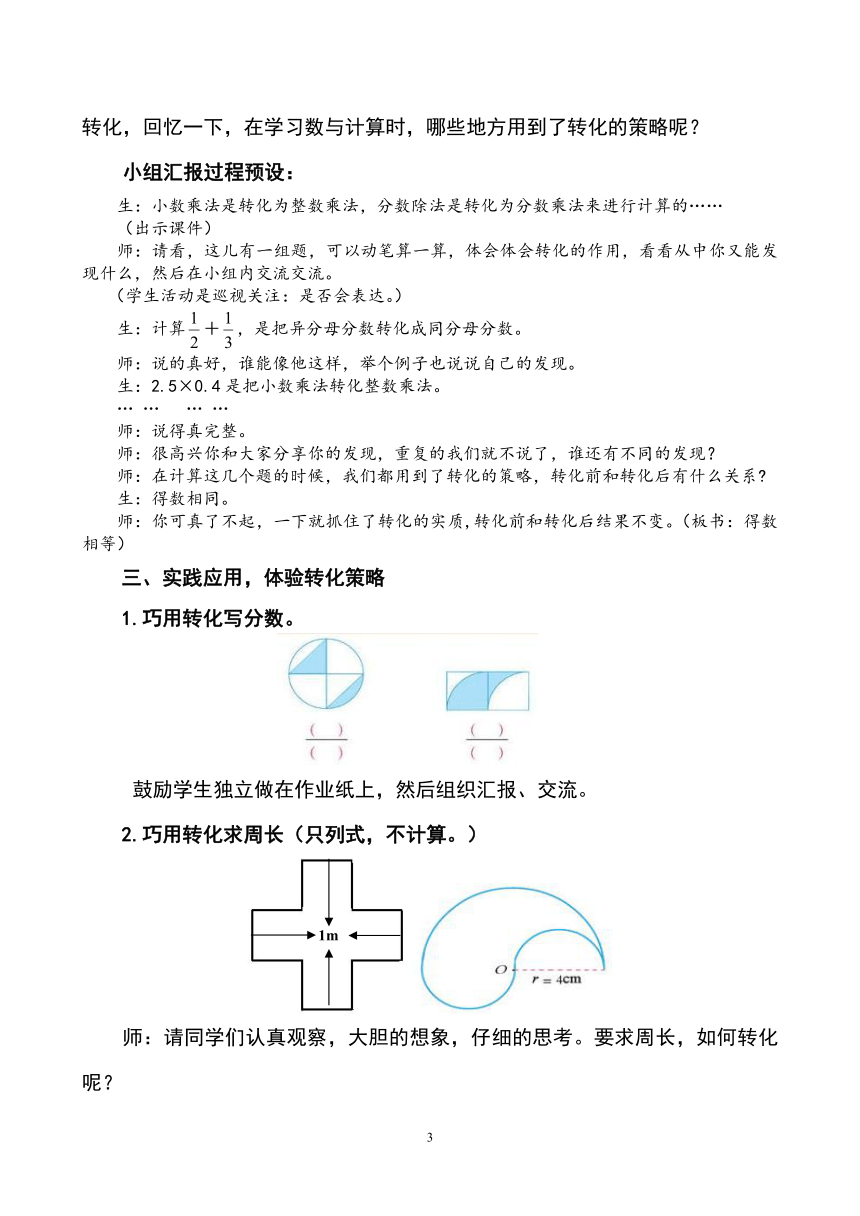
1.巧用转化写分数。
鼓励学生独立做在作业纸上,然后组织汇报、交流。
2.巧用转化求周长(只列式,不计算。)
师:请同学们认真观察,大胆的想象,仔细的思考。要求周长,如何转化呢?
生独立完成,小组汇报过程预设:
师:这么快就会了,谁来说?
生:… … … …
(第二幅图过程预设)
师:如果要求这个图形的周长,该怎样转化呢?
生1:把左边的半圆平移到右边,转化成一个小圆,用大圆周长的一半加上小圆的周长。
师:还有不同的想法吗?
生2:整个一个图形可以转化成一个大圆。
师:怎么就能转化成大圆的周长?
引导学生思考大小圆之间的关系。
生:大圆的周长是小圆周长的2倍。
师:你怎么知道大圆的周长就是小圆周长的2倍?
生:大圆半径是小圆的2倍,大圆周长也是小圆的2倍,小圆的周长是大圆的二分之一,合起来就是一个大圆的周长。
师:咱们同学们真了不起,想到了不同的转化方法,并且这种转化的方法使问题变得非常简单。
3、计算中的转化
出示题目:+++
生:通分!(异口同声)
师:除了通分,那有没有更简便的方法呢?
课件出示正方形图
引导学生分析涂色部分的大小可以用1减去空白部分的大小,1-
师:明明是个加法算式,怎么变成减法算式了?
生:因为这里还空缺一个。
师:听明白了吗?这位同学借助图形帮助进行算式的转化,非常善于观察和思考。
4、关注生活
(1)下图的蒙古包是由一个圆柱和一个圆锥组成。蒙古包所占的空间大约是多少立方米?(只列式,不计算)
(2)求阴影部分的面积。
(3)课本74页,第一题。
生独立思考的基础上,课小组讨论汇报。这三个问题比较难,教师可以给予相应的提示。
四、畅谈收获,提升转化策略
师:通过今天的研究探索,你一定有很多的感想。最后我们用一个小故事来结束本节的学习。
小故事:从前,有位老太太有两个儿子,大儿子是卖雨伞的,小儿子是卖西瓜的。于是,老太太成天忧心忡忡,每逢下雨天,她担心西瓜卖不掉;天晴时,又担心雨伞卖不出去。日子过得非常忧郁。(让学生为老太太出谋划策)
后来,一位聪明人告诉她:“老太太,你真是好福气!下雨天,你大儿子家生意兴隆;天晴时,你小儿子家顾客盈门,哪一天都有好消息呀!”这位老太太一想,立刻笑逐颜开了。
所以有些时候,换个角度去想问题,你会发现真的很不一样!其实自己快乐与否,重在心态。只要你用乐观的心态去面对,无论任何事情,都会是快乐的!希望大家在生活中快乐地转化,在数学中灵活地转化!
课堂小结:
学习数学讲策略,数学策略真不少。
复杂转化为简单,陌生转化为熟悉,
抽象转化为具体,未知转化为已知。
转化策略在身边,处处留心记心间
附件1:板书
附件2:学生用学案。
附件1
板书:
转化的策略
,
,
附件2
解决问题的策略
———转化的策略
【设问导读】
1.观察下面两个图像,比较它们图形的面积大小。
2.同学们,其实,在以前的学习中,我们就经常用到转化的策略解决问题,比如说一些图形的面积公式、体积公式的推导,就常常用到转化的策略,你们能想起来吗?自己先想一想,然后跟小组的伙伴交流交流。
3.从某种意义上来说,学习数学就是不断学会转化的过程。不仅在图形的世界里常常应用转化的策略解决问题,而且,在看似简单的计算中也蕴含着转化,回忆一下,在学习数与计算时,哪些地方用到了转化的策略呢?
【自学检测】
1.巧用转化写分数。
2.巧用转化求周长(只列式,不计算。)
【巩固提升】
1.巧用转化计算:+++=
2.下图的蒙古包是由一个圆柱和一个圆锥组成。蒙古包所占的空间大约是多少立方米?(只列式,不计算)
3.求阴影部分的面积。
4.课本74页,第一题。
【课堂小结】
这节课你有什么收获?
9
【教学目标】
1.让学生经历回顾与探索运用转化策略解决问题的过程,初步感受转化策略的价值。
2.使学生初步学会运用转化的策略分析问题,并能根据问题的特点确定具体的转化方法,从而有效地解决问题。
3.使学生进一步积累运用转化策略解决问题的经验,增强解决问题的策略意识,获得成功的体验。
【教学重点】 感受“转化”策略的价值,会用“转化”的策略解决问题。
【教学难点】 会用“转化”的策略解决问题。
【教学过程】
课前交流,孕伏转化策略:
教师:同学们,大家好,很高兴再次能和大家再一起学习,为了缓和紧张的气氛,我给大家讲个小故事吧!(学生拭目以待)
教师:播放PPT,用优美的语言和动作来诠释故事内容。
教师:好的故事总能给人以启迪,从这个故事中,你受到了哪些启发呢?学生自由交流感受,教师适时小结:儿子能将复杂的事情与简单的事情相转化,从而巧妙的解决了问题,真是了不起,相信同学们也会有不俗的表现。
一、情境出示,合作探究
1、巧设例题,感知“转化”。
数学与生活息息相关,为了优化教学过程,我创造性地使用了教材,创设了我去喷绘版面,要按照面积收费,从而对面积的大小产生争议这一生活中的问题情境,引出例题1。(点课件)
先让学生猜测谁的面积大,再组织学生小组讨论、验证自己的猜测,我根据学生的汇报利用Powerpoint课件,形象直观的演示转化过程。
学生汇报预设:
师:有答案了吗?哪个图形的面积大?谁来说说。
生1:第一个图形的面积大。
生2:第二个图形的面积大。
生3:两个图形的面积相等。
师:你是如何比较出来的?
生:(边演示边说)我们把这块切开放到这块,都变成了长5个格、宽4个格的长方形。
教师注意引导学生说出方法,如何平移、旋转的?
师:听明白了吗?想的巧妙,讲的也非常清楚。谁再来说一说?)
师:原来的图形不规则,不容易比较大小。同学们都是利用了图形凹凸的特点想到了这个好办法,非常善于观察、思考。下面我们再来清晰的演示一下这个变化过程。请看,(课件演示)平移,旋转,瞧,哪个图形面积大?(相等)真是一目了然,原来的两个不规则图形通过平移、旋转都变成了规则的的图形。 (板书:不规则图形 规则图形)你们知道吗,这是一种解决问题的策略,这种策略就叫转化(板书课题)
进一步引导:
师:这样转化,什么变了?什么没变?
生:周长变了,面积没变。
师:还有什么变了?(形状变了。)
师:你抓住了问题的关键,的确,这样转化,形状变了,面积却没变。(板书:形变积不变)
二、唤醒记忆,回顾转化策略
1.图形面积、体积方面的应用。
师:同学们,其实,在以前的学习中,我们就经常用到转化的策略解决问题,比如说一些图形的面积公式、体积公式的推导,就常常用到转化的策略,你们能想起来吗?自己先想一想,然后跟小组的伙伴交流交流。
小组汇报过程预设:
生:在学习图形的面积时,三角形的面积。把两个完全一样的三角形拼成一个平行四边形。
师:这是把一个三角形的面积转化成了平行四边形面积的一半。没错,这就是转化。
师:还有谁想说?
生:把两个完全一样的梯形拼成一个平行四边形。
师:这是把什么转化成什么?
生:梯形转化成平行四边形
师:准确的说,这是把梯形转化成平行四边形面积的(一半)这也是转化。还有吗?
生:把平行四边行转化成长方形。
生:圆也是把圆分成若干个小扇形,然后再拼成一个近似的长方形。
生:圆柱是把圆柱转化成长方体。
师:这也是用转化解决的新问题。
课件出示:
平行四边形的面积公式推导 三角形的面积公式推导
梯形的面积公式推导 圆的面积公式推导
圆柱的体积公式推导 圆锥的体积公式推导
师:大家来看,我们曾经用转化的策略解决了这么多新问题。选一个你最喜欢的、或者感觉有困难的,二人小组互相说一说。
2.数与计算方面的应用。
师:从某种意义上来说,学习数学就是不断学会转化的过程。不仅在图形的世界里常常应用转化的策略解决问题,而且,在看似简单的计算中也蕴含着转化,回忆一下,在学习数与计算时,哪些地方用到了转化的策略呢?
小组汇报过程预设:
生:小数乘法是转化为整数乘法,分数除法是转化为分数乘法来进行计算的……
(出示课件)
师:请看,这儿有一组题,可以动笔算一算,体会体会转化的作用,看看从中你又能发现什么,然后在小组内交流交流。
(学生活动是巡视关注:是否会表达。)
生:计算+,是把异分母分数转化成同分母分数。
师:说的真好,谁能像他这样,举个例子也说说自己的发现。
生:2.5×0.4是把小数乘法转化整数乘法。
… … … …
师:说得真完整。
师:很高兴你和大家分享你的发现,重复的我们就不说了,谁还有不同的发现?
师:在计算这几个题的时候,我们都用到了转化的策略,转化前和转化后有什么关系?
生:得数相同。
师:你可真了不起,一下就抓住了转化的实质,转化前和转化后结果不变。(板书:得数相等)
三、实践应用,体验转化策略
1.巧用转化写分数。
鼓励学生独立做在作业纸上,然后组织汇报、交流。
2.巧用转化求周长(只列式,不计算。)
师:请同学们认真观察,大胆的想象,仔细的思考。要求周长,如何转化呢?
生独立完成,小组汇报过程预设:
师:这么快就会了,谁来说?
生:… … … …
(第二幅图过程预设)
师:如果要求这个图形的周长,该怎样转化呢?
生1:把左边的半圆平移到右边,转化成一个小圆,用大圆周长的一半加上小圆的周长。
师:还有不同的想法吗?
生2:整个一个图形可以转化成一个大圆。
师:怎么就能转化成大圆的周长?
引导学生思考大小圆之间的关系。
生:大圆的周长是小圆周长的2倍。
师:你怎么知道大圆的周长就是小圆周长的2倍?
生:大圆半径是小圆的2倍,大圆周长也是小圆的2倍,小圆的周长是大圆的二分之一,合起来就是一个大圆的周长。
师:咱们同学们真了不起,想到了不同的转化方法,并且这种转化的方法使问题变得非常简单。
3、计算中的转化
出示题目:+++
生:通分!(异口同声)
师:除了通分,那有没有更简便的方法呢?
课件出示正方形图
引导学生分析涂色部分的大小可以用1减去空白部分的大小,1-
师:明明是个加法算式,怎么变成减法算式了?
生:因为这里还空缺一个。
师:听明白了吗?这位同学借助图形帮助进行算式的转化,非常善于观察和思考。
4、关注生活
(1)下图的蒙古包是由一个圆柱和一个圆锥组成。蒙古包所占的空间大约是多少立方米?(只列式,不计算)
(2)求阴影部分的面积。
(3)课本74页,第一题。
生独立思考的基础上,课小组讨论汇报。这三个问题比较难,教师可以给予相应的提示。
四、畅谈收获,提升转化策略
师:通过今天的研究探索,你一定有很多的感想。最后我们用一个小故事来结束本节的学习。
小故事:从前,有位老太太有两个儿子,大儿子是卖雨伞的,小儿子是卖西瓜的。于是,老太太成天忧心忡忡,每逢下雨天,她担心西瓜卖不掉;天晴时,又担心雨伞卖不出去。日子过得非常忧郁。(让学生为老太太出谋划策)
后来,一位聪明人告诉她:“老太太,你真是好福气!下雨天,你大儿子家生意兴隆;天晴时,你小儿子家顾客盈门,哪一天都有好消息呀!”这位老太太一想,立刻笑逐颜开了。
所以有些时候,换个角度去想问题,你会发现真的很不一样!其实自己快乐与否,重在心态。只要你用乐观的心态去面对,无论任何事情,都会是快乐的!希望大家在生活中快乐地转化,在数学中灵活地转化!
课堂小结:
学习数学讲策略,数学策略真不少。
复杂转化为简单,陌生转化为熟悉,
抽象转化为具体,未知转化为已知。
转化策略在身边,处处留心记心间
附件1:板书
附件2:学生用学案。
附件1
板书:
转化的策略
,
,
附件2
解决问题的策略
———转化的策略
【设问导读】
1.观察下面两个图像,比较它们图形的面积大小。
2.同学们,其实,在以前的学习中,我们就经常用到转化的策略解决问题,比如说一些图形的面积公式、体积公式的推导,就常常用到转化的策略,你们能想起来吗?自己先想一想,然后跟小组的伙伴交流交流。
3.从某种意义上来说,学习数学就是不断学会转化的过程。不仅在图形的世界里常常应用转化的策略解决问题,而且,在看似简单的计算中也蕴含着转化,回忆一下,在学习数与计算时,哪些地方用到了转化的策略呢?
【自学检测】
1.巧用转化写分数。
2.巧用转化求周长(只列式,不计算。)
【巩固提升】
1.巧用转化计算:+++=
2.下图的蒙古包是由一个圆柱和一个圆锥组成。蒙古包所占的空间大约是多少立方米?(只列式,不计算)
3.求阴影部分的面积。
4.课本74页,第一题。
【课堂小结】
这节课你有什么收获?
9
