七年级下学期_多边形及其内角和
文档属性
| 名称 | 七年级下学期_多边形及其内角和 |

|
|
| 格式 | zip | ||
| 文件大小 | 123.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-15 00:00:00 | ||
图片预览




文档简介
多边形及其内角和
目标认知
学习目标:
1.了解多边形,多边形的对角线,正多边形等有关的概念;
2.掌握多边形内角和与外角和公式;
3.灵活运用多边形内角和与外角和公式解决有关问题,体验并掌握探索、归纳图形性质的推理方法,
进一步培养说理和进行简单推理的能力.
重点:
多边形内角和及外角和公式的灵活应用.
难点:
1.多边形内角和公式的推导.
2.多边形内角和及外角和公式的应用
知识要点梳理
知识点一:多边形及有关概念
1、 多边形的定义:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.
(1)多边形的一些要素:
边:组成多边形的各条线段叫做多边形的边.
顶点:每相邻两条边的公共端点叫做多边形的顶点.
内角:多边形相邻两边组成的角叫多边形的内角,一个n边形有n个内角。
外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角。
(2)在定义中应注意:
①一些线段(多边形的边数是大于等于3的正整数);
②首尾顺次相连,二者缺一不可;
③理解时要特别注意“在同一平面内”这个条件,其目的是为了排除几个点不共面的情况,即空间
多边形.
2、多边形的分类:
(1)多边形可分为凸多边形和凹多边形,画出多边形的任何一条边所在的直线,如果整个多边形都在这
条直线的同一侧,则此多边形为凸多边形,反之为凹多边形(见图1).本章所讲的多边形都是指凸
多边形.
凸多边形 凹多边形
图1
(2)多边形通常还以边数命名,多边形有n条边就叫做n边形.三角形、四边形都属于多边形,其中三角
形是边数最少的多边形.
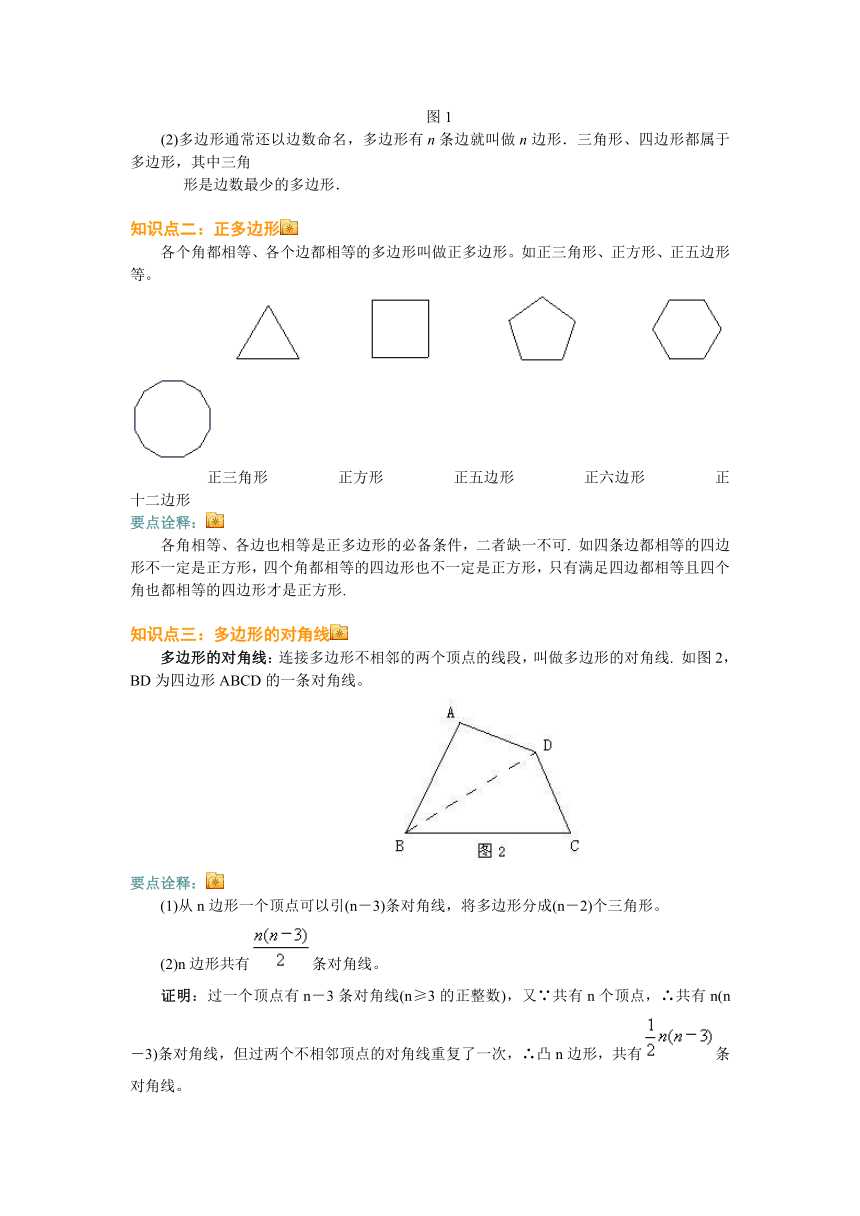
知识点二:正多边形
各个角都相等、各个边都相等的多边形叫做正多边形。如正三角形、正方形、正五边形等。
正三角形 正方形 正五边形 正六边形 正十二边形
要点诠释:
各角相等、各边也相等是正多边形的必备条件,二者缺一不可. 如四条边都相等的四边形不一定是正方形,四个角都相等的四边形也不一定是正方形,只有满足四边都相等且四个角也都相等的四边形才是正方形.
知识点三:多边形的对角线
多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线. 如图2,BD为四边形ABCD的一条对角线。
要点诠释:
(1)从n边形一个顶点可以引(n-3)条对角线,将多边形分成(n-2)个三角形。
(2)n边形共有条对角线。
证明:过一个顶点有n-3条对角线(n≥3的正整数),又∵共有n个顶点,∴共有n(n-3)条对角线,但过两个不相邻顶点的对角线重复了一次,∴凸n边形,共有条对角线。
知识点四:多边形的内角和公式
1.公式:边形的内角和为.
2.公式的证明:
证法1:在边形内任取一点,并把这点与各个顶点连接起来,共构成个三角形,这个三角形的内角和为,再减去一个周角,即得到边形的内角和为.
证法2:从边形一个顶点作对角线,可以作条对角线,并且边形被分成个三角形,这个三角形内角和恰好是边形的内角和,等于.
证法3:在边形的一边上取一点与各个顶点相连,得个三角形,边形内角和等于这个三角形的内角和减去所取的一点处的一个平角的度数,
即.
要点诠释:
(1)注意:以上各推导方法体现出将多边形问题转化为三角形问题来解决的基础思想。
(2)内角和定理的应用:
①已知多边形的边数,求其内角和;
②已知多边形内角和,求其边数。
知识点五:多边形的外角和公式
1.公式:多边形的外角和等于360°.
2.多边形外角和公式的证明:多边形的每个内角和与它相邻的外角都是邻补角,所以边形的内角和加外角和为,外角和等于.注意:n边形的外角和恒等于360°,它与边数的多少无关。
要点诠释:
(1)外角和公式的应用:
①已知外角度数,求正多边形边数;
②已知正多边形边数,求外角度数.
(2)多边形的边数与内角和、外角和的关系:
①n边形的内角和等于(n-2)·180°(n≥3,n是正整数),可见多边形内角和与边数n有关,每增加
1条边,内角和增加180°。
②多边形的外角和等于360°,与边数的多少无关。
知识点六:镶嵌的概念和特征
1、定义:用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做用多边形覆盖平面(或平面镶嵌)。这里的多边形可以形状相同,也可以形状不相同。
2、实现镶嵌的条件:拼接在同一点的各个角的和恰好等于360°;相邻的多边形有公共边。
3、常见的一些正多边形的镶嵌问题:
(1)用正多边形实现镶嵌的条件:边长相等;顶点公用;在一个顶点处各正多边形的内角之和为360°。
(2)只用一种正多边形镶嵌地面
对于给定的某种正多边形,怎样判断它能否拼成一个平面图形,且不留一点空隙?解决问题的关键在于正多边形的内角特点。当围绕一点拼在一起的几个正多边形的内角加在一起恰好组成一个周角360°时,就能铺成一个平面图形。
事实上,正n边形的每一个内角为,要求k个正n边形各有一个内角拼于一点,恰好覆盖地面,这样360°=,由此导出k==2+,而k是正整数,所以n只能取3,4,6。因而,用相同的正多边形地砖铺地面,只有正三角形、正方形、正六边形的地砖可以用。
注意:任意四边形的内角和都等于360°。所以用一批形状、大小完全相同但不规则的四边形地砖也可以铺成无空隙的地板,用任意相同的三角形也可以铺满地面。
(3)用两种或两种以上的正多边形镶嵌地面
用两种或两种以上边长相等的正多边形组合成平面图形,关键是相关正多边形“交接处各角之和能否拼成一个周角”的问题。例如,用正三角形与正方形、正三角形与正六边形、正三角形与正十二边形、正四边形与正八边形都可以作平面镶嵌,见下图:
又如,用一个正三角形、两个正方形、一个正六边形结合在一起恰好能够铺满地面,因为它们的交接处各角之和恰好为一个周角360°。
规律方法指导
1.内角和与边数成正比:边数增加,内角和增加;边数减少,内角和减少. 每增加一条边,内角的和
就增加180°(反过来也成立),且多边形的内角和必须是180°的整数倍.
2.多边形外角和恒等于360°,与边数的多少无关.
3.多边形最多有三个内角为锐角,最少没有锐角(如矩形);多边形的外角中最多有三个钝角,最少
没有钝角.
4.在运用多边形的内角和公式与外角的性质求值时,常与方程思想相结合,运用方程思想是解决本节
问题的常用方法.
5.在解决多边形的内角和问题时,通常转化为与三角形相关的角来解决. 三角形是一种基本图形,是
研究复杂图形的基础,同时注意转化思想在数学中的应用.
经典例题透析
类型一:多边形内角和及外角和定理应用
1.一个多边形的内角和等于它的外角和的5倍,它是几边形?
思路点拨:本题实际告诉了这个多边形的内角和是.
解析:设这个多边形是边形,
则它的内角和是,
所以,解得.
所以这个多边形是十二边形.
总结升华:本题是多边形的内角和定理和外角和定理的综合运用. 只要设出边数,根据条件列出关于的方程,求出的值即可,这是一种常用的解题思路.
举一反三:
【变式1】若一个多边形的内角和与外角和的总度数为1800°,求这个多边形的边数.
【答案】设这个多边形的边数为,根据题意得:
,
解得.
所以多边形的边数为10.
【变式2】一个多边形除了一个内角外,其余各内角和为2750°,求这个多边形的内角和是多少?
【答案】设这个多边形的边数为,这个内角为,
则,
即.
因为等式左边是180°的整数倍,所以等式右边也是180°的整数倍.
又因为,
所以,此时.
所以这个多边形的内角和是:.
【变式3】个多边形的内角和与某一个外角的度数总和为1350°,求这个多边形的边数。
【答案】可设多边形的边数为n,某一个外角为α
则(n-2)×180+α=1350
从而(n-2)=
因为边数n为正整数,所以α=90,n=9
类型二:多边形对角线公式的运用
2.某校七年级六班举行篮球比赛,比赛采用单循环积分制(即每两个班都进行一次比赛).你能算出一共需要进行多少场比赛吗?
思路点拨:本题体现与体育学科的综合,解题方法参照多边形对角线条数的求法,即多边形的对角线条数加上边数. 如图:
解析:共需要比赛(场).
所以一共需要进行15场比赛.
总结升华:对于其他学科问题要善于把它与数学知识联系在一起,便于解决.
举一反三:
【变式1】一个多边形共有20条对角线,则多边形的边数是( ).
A.6 B.7 C.8 D.9
【答案】C. 提示:一个多边形的对角线条数为条,将6、7、8、9分别代入,结果为20的即为正确答案.
【变式2】一个十二边形有几条对角线。
解析:过十二边形的任意一个顶点可以画9条对角线,那么十二个顶点可以画12×9条对角线,
但每条对角线在每个顶点都数了一次,所以实际对角线的条数应该为12×9÷2=54(条)
∴十二边形的对角线共有54条。
总结升华:对于一个n边形的对角线的条数,我们可以总结出规律条,牢记这个公式,以后只要用相应的n的值代入即可求出对角线的条数,要记住这个公式只有在理解的基础之上才能记得牢。
类型三:可转化为多边形内角和问题
3.如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
思路点拨: 设法将这几个角转移到一个多边形中,然后利用多边形内角和公式求解.
解析:连接BF,则∠A+∠G=∠1+∠2.
∴∠A+∠ABC+∠C+∠D+∠E+∠EFG+∠G
=∠1+∠2+∠ABC+∠C+∠D+∠E+∠EFG.
=(5-2) ·180°= 540°.
总结升华:本题通过作辅助线,把∠A与∠G的和转化为∠1与∠2的和,从而把问题变为求五边形的内角和运算,“转化思想”是解决本题的关键.
举一反三:
【变式1】如图所示,∠1+∠2+∠3+∠4+∠5+∠6=__________.
【答案】360°.(提示:把∠1、∠2、∠3、∠4、∠5、∠6转移到同一个多边形内.)
【变式2】如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数。
解析:连结ED,在ΔAOB和ΔDOE中,
∵∠AOB=∠DOE,
∴∠1+∠2=∠A+∠B
∴∠A+∠B+∠C+∠CDO+∠OEF+∠F
=∠2+∠1+∠C+∠CDO+∠OEF+∠F
=∠C+∠CDE+∠DEF+∠F=360°
类型四:实际应用题
4.如图,一辆小汽车从P市出发,先到B市,再到C市,再到A市,最后返回P市,这辆小汽车共转了多少度角?
思路点拨:根据多边形的外角和定理解决.
解析:如图,
当小汽车从P出发行驶到B市,由B市向C市行驶时转的角是,由C市向A市行驶时转的角是,
由A市向P市行驶时转的角是.
因此,小汽车从P市出发,经B市、C 市、A市,又回到P市,共转.
总结升华:旋转的角度是指原来前进的方向与转弯后的方向的夹角.小汽车沿任意多边形行驶一周回到原处,转过的角度都是360°。
举一反三:
【变式1】如图所示,小亮从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,当他第一次回到出发点时,一共走了__________m.
【答案】240. 提示:小亮每次向右转的角度相同,并且前进的路程也相同,因此当他第一次回到出发点A时,所走的路程是一个正多边形的周长,每次转的角度是这个正多边形的一个外角,所以这个正多边形的边数是360°÷15°=24,所以小亮一共走了10×24=240(m)
【变式2】小华从点A出发向前走10米,向右转36°,然后继续向前走10米,再向右转36°,他以同样的方法继续走下去,他能回到点A吗?若能,当他走回点A时共走了多少米?若不能,写出理由。
解析:可以走回到A点,共走100米,理由,根据多边形的外角和是360°可知,每次向右转36°,
并且都走10米,可得,小华共转10次,故共走100米。
所以,可以走回到A点,共走100米。
【变式3】如图所示是某厂生产的一块模板,已知该模板的边AB∥CF,CD∥AE. 按规定AB、CD的延长线相交成80°角,因交点不在模板上,不便测量. 这时师傅告诉徒弟只需测一个角,便知道AB、CD的延长线的夹角是否合乎规定,你知道需测哪一个角吗?说明理由.
思路点拨:本题中将AB、CD延长后会得到一个五边形,根据五边形内角和为540°,又由AB∥CF,CD∥AE,可知∠BAE+∠AEF+∠EFC=360°,从540°中减去80°再减去360°,剩下∠C的度数为100°,所以只需测∠C的度数即可,同理还可直接测∠A的度数.
解析:测∠A或∠C的度数,只需∠A=100°或∠C=100°,
即知模板中AB、CD的延长线的夹角是否符合规定.
理由如下:连接AF,∵AB∥CF,
∴∠BAF+∠AFC=180°.
又∵∠EAF+∠E+∠AFE=180°,
∴∠BAE+∠E+∠EFC=360°.
若∠C=100°,
则AB、CD的延长线的夹角=540°- 360°- 100°= 80°,
即符合规定.
同理:若连接CE,可得∠AEF+∠F+∠DCF=360°.
若∠A=100°,则也符合规定.
总结升华:本题实际上是多边形内角和的逆运算,关键在于正确添加辅助线.
类型五:镶嵌问题
5.分别画出用相同边长的下列正多边形组合铺满地面的设计图。
(1)正方形和正八边形;
(2)正三角形和正十二边形;
(3)正三角形、正方形和正六边形。
思路点拨:只要在拼接处各多边形的内角的和能构成一个周角,那么这些多边形就能作平面镶嵌。
解析:正三角形、正方形、正六边形、正八边形、正十二边形的每一个内角分别是60°、90°、120°、135°、150°。
(1)因为90+2×135=360,所以一个顶点处有1个正方形、2个正八边形,如图(1)所示。
(2)因为60+2×150=360,所以一个顶点处有1个正三角形、2个正十二边形,如图(2)所示。
(3)因为60+2×90+120=360,所以一个顶点处有1个正三角形、1个正六边形和2个正方形,如图(3)
所示。
总结升华:用两种以上边长相等的正多边形组合成平面图形,实质上是相关正多边形“交接处各角之和能否拼成一个周角”的问题。
举一反三:
【变式1】分别用形状、大小完全相同的①三角形木板;②四边形木板;③正五边形木板;④正六边形木板作平面镶嵌,其中不能镶嵌成地板的是( )
A、① B、② C、③ D、④
【答案】C
解析:用同一种多边形木板铺地面,只有正三角形、四边形、正六边形的木板可以用,不能用正五边形木板,故选C。
【变式2】用三块正多边形的木板铺地,拼在一起并相交于一点的各边完全吻合,其中两块木板的边数都是8,则第三块木板的边数应是( )
A、4 B、5 C、6 D、8
【答案】A (提示:先算出正八边形一个内角的度数,再乘以2,然后用360°减去刚才得到的积,便得到第三块木板一个内角的度数,进而得到第三块木板的边数)
【变式3】(2010内蒙古赤峰)下面平面图形中,不能镶嵌平面的图形是 ( )
A.任意一个三角形 B.任意一个四边形
C.任意一个正五边形 D.任意一个正六边形
【答案】C
解析:把两个三角形的6个内角放在一处,恰好是360°;四边形的内角和为360°,能够镶嵌平面;正六边形每一个内角是120°,120是360的约数,也能够镶嵌平面;正五边形的每一个内角是108°,108不是360的约数,不能镶嵌平面.
学习成果测评
基础达标:
选择题
1.多边形的内角和不可能是( ).
A.1800° B.540° C.800° D.360°
2.一个多边形的内角中,锐角的个数最多有( ).
A.3个 B.4个 C.5个 D.6个
3.四边形中,如果有一组对角都是直角,那么另一组对角可能( ).
A.都是钝角; B.都是锐角
C.是一个锐角、一个钝角 D.是一个锐角、一个直角
4.若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是( ).
A.十三边形 B.十二边形 C.十一边形 D.十边形
5.如图,国旗上的五角星的五个角的度数是相同的,每一个角的度数都是( ).
A.30° B.35° C.36° D.42°
6.如图,∠A+∠B+∠C+∠D+∠E+∠F=( ).
A.180° B.360° C.540° D.720°
7.如图,至少去掉( )个点,才能使留下的任何三个点都不能组成一个正三角形( ).
A.2 B.3 C.4 D.5
8.从一个边形中除去一个角后,其余个内角和是2580°,则原多边形的边数是( ).
A.15 B.17 C.19 D.13
9.(2010广东肇庆)一个多边形的内角和是外角和的2倍,则这个多边形是 ( )
A.四边形 B.五边形 C.六边形 D.八边形
10.(2010福建泉州)如图所示,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC
上,将△ABC沿着DE折叠压平,A与重合,若∠A=70°,则∠1+∠2= ( )
A.140° B.130° C.110° D.70°
填空题
11.如果一个多边形的每一个内角都相等,且每一个内角都大于135°, 那么这个多边形的边数最少为__.
12.已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比为9:2,则这个多边形的边数
为_______.
13.一个多边形,每个内角的度数都比它相邻的外角度数的2倍多45°,则它是_______边形.
14.(为整数,且)边形的内角和比边形的内角和小_________度.
15.一个多边形的每一个外角的度数等于与其相邻内角的度数的,则这个多边形是___________边形.
16.如图所示,一个顶角为40°的等腰三角形纸片,剪去一个顶角后,得到一个四边形,则
∠1+∠2=___________.
17.一个多边形的每个内角都等于120°,则从此多边形一个顶点出发引出___________条对角线.
18.小勇制造了一个简单的机器人,小勇遥控它每前行1m就向左转30°,再向前行1m又向左转30°,问
它需要走___________m才能走回原地.
解答题
19.凸边形的个内角与某一个外角的总和为1450°,则的值是多少?
20.四个村庄地理位置如图,点A、B、C、D处,为了解决四个村庄饮水问题,现准备兴建一座地下水供水厂,问建在何处,材料费用最低,画出示意图,并说明理由.
能力提升
1.如图所示,用火柴杆摆出一系列三角形图案,按这种方式摆下去,当摆到20层()时,需要多少根火柴
2.如图所示,某厂规定一块模板中AB、CD的延长线相交成80°角,因交点不在板上,不便测量,工人师傅连接AC,测得∠BAC=34°,∠DCA=65°,此时AB、CD的延长线相交的角是否符合规定?为什么?
3.将一块正六边形硬纸片如图(1),做成一个底面仍为正六边形且高相等的无盖纸盒(侧面均垂直于底面,如图(2),需要在每一个顶点处减去一个四边形,如图(1)中的四边形AGA′H,求∠GA′H的大小.
(1) (2)
4.(开放性问题)一个长方形被截掉一个角后,得到一个多边形,此多边形的内角和是多少度?
综合探究:
1.如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
2.已知六边形ABCDEF,如图,它的每个内角都相等,且AB=1,BC=CD=DE=9,求这个六边形的周长.
答案与解析
基础达标:
选择题
1.C.
提示:根据多边形内角和定理,可知,内角和一定是180°的整数倍,故其不可能为多边
形的内角和.
2.A.
3.C.
4.A.
5.C.
提示:将五角星的五个角转移到一个三角形中,由三角形内角和定理以及五角星的各个角都相等,
即可求出各个角的度数.
6.B.
提示:∠A+∠B、∠C+∠D、∠E+∠F转移到中间三角形的外角位置上.
7.C.
8.B.
提示:设除去的内角为,则,即,
又∵为整数,∴,.
9.C.
提示:已知任意多边形的外角和是360°,可以知道其内角和是720°.
利用内角和公式可知这个多边形是一个六边形.
10.A.
提示:由∠A=70°得∠AED+∠ADE=110°,再由折叠可知,
故
填空题
11.9.
12.11.
13.八.
提示:由于外角和度数为360°,则可设出边数,
再根据内角和公式列方程解题. 设边数为,
则有,解得.
14.180°.
提示:.
15.八.
提示:设每个外角为,则,
解得,而多边形边数.
16.220°.
提示:由顶角为40°可知两底角和为140°,
∴∠1+∠2=360°-140°=220°.
此题考察三角形、四边形的内角和定理.
17.3.
18.12.
提示:机器人走过了一个外角为30°的正多边形,由任意多边形的外角和均为360°,
所以有,得,所以它需要走12m才能走回原地.
解答题
19.解:设这个外角为,则有,
因为为整数,所以解得,.
20.连结AC、BD交于点O,则点O就是要求的点.
能力提升
1.630根.
提示:实际摆放层数和增加的三角形的数量是一样的,
所以在第20层时,一共有1+2+…+20个三角形.
2.解:不符合规定,因为AB、CD的延长线相交成的角为81°.
3.60°.
提示:四边形AGA′H中,边A′H与A′G一定与正六边形各边垂直,
又由正六边形一个内角为120°,可得∠GA′H的大小为60°.
4.提示:本题是开放性问题,应分情况进行讨论,要注意长方形去掉一个角后所有可能情况.
解:长方形去掉一个角后得到的多边形有3种情况,如图:
它们分别是三角形、四边形、五边形,所以内角和分别为180°、360°、 540°.
综合探究
1.解:如图,
∵∠3=360°-∠D-∠E-∠F,
∴∠1=180°-∠3=180°-(360°-∠D-∠E-∠F)
=∠D+∠E+∠F-180°.
又∵∠2=∠B+∠C,
∴∠A+∠1+∠2=∠A+∠D+∠E+∠F-180°+∠B+∠C=180°,
即∠A+∠B+∠C+∠D+∠E+∠F=360°.
2.解:如图所示,
延长AB、DC交于G,延长CD、FE交于H,延长BA、EF交于L.
由六边形的每个内角都相等知,
它的每个外角都等于.
∴△CBG、△DHE、△AFL和△GHL都是等边三角形,
∴GH=GC+CD+DH=BC+CD+DE=27,GL=27,
即GB+AB+AL=BC+AB+AF=27,∴9+1+AF=27,
∴AF=17.
同理,由LH=27,即LF+FE+EH=27,得EF=1.
∴六边形ABCDEF的周长为1+9×3+1+17=46.
目标认知
学习目标:
1.了解多边形,多边形的对角线,正多边形等有关的概念;
2.掌握多边形内角和与外角和公式;
3.灵活运用多边形内角和与外角和公式解决有关问题,体验并掌握探索、归纳图形性质的推理方法,
进一步培养说理和进行简单推理的能力.
重点:
多边形内角和及外角和公式的灵活应用.
难点:
1.多边形内角和公式的推导.
2.多边形内角和及外角和公式的应用
知识要点梳理
知识点一:多边形及有关概念
1、 多边形的定义:在平面内,由一些线段首尾顺次相接组成的图形叫做多边形.
(1)多边形的一些要素:
边:组成多边形的各条线段叫做多边形的边.
顶点:每相邻两条边的公共端点叫做多边形的顶点.
内角:多边形相邻两边组成的角叫多边形的内角,一个n边形有n个内角。
外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角。
(2)在定义中应注意:
①一些线段(多边形的边数是大于等于3的正整数);
②首尾顺次相连,二者缺一不可;
③理解时要特别注意“在同一平面内”这个条件,其目的是为了排除几个点不共面的情况,即空间
多边形.
2、多边形的分类:
(1)多边形可分为凸多边形和凹多边形,画出多边形的任何一条边所在的直线,如果整个多边形都在这
条直线的同一侧,则此多边形为凸多边形,反之为凹多边形(见图1).本章所讲的多边形都是指凸
多边形.
凸多边形 凹多边形
图1
(2)多边形通常还以边数命名,多边形有n条边就叫做n边形.三角形、四边形都属于多边形,其中三角
形是边数最少的多边形.
知识点二:正多边形
各个角都相等、各个边都相等的多边形叫做正多边形。如正三角形、正方形、正五边形等。
正三角形 正方形 正五边形 正六边形 正十二边形
要点诠释:
各角相等、各边也相等是正多边形的必备条件,二者缺一不可. 如四条边都相等的四边形不一定是正方形,四个角都相等的四边形也不一定是正方形,只有满足四边都相等且四个角也都相等的四边形才是正方形.
知识点三:多边形的对角线
多边形的对角线:连接多边形不相邻的两个顶点的线段,叫做多边形的对角线. 如图2,BD为四边形ABCD的一条对角线。
要点诠释:
(1)从n边形一个顶点可以引(n-3)条对角线,将多边形分成(n-2)个三角形。
(2)n边形共有条对角线。
证明:过一个顶点有n-3条对角线(n≥3的正整数),又∵共有n个顶点,∴共有n(n-3)条对角线,但过两个不相邻顶点的对角线重复了一次,∴凸n边形,共有条对角线。
知识点四:多边形的内角和公式
1.公式:边形的内角和为.
2.公式的证明:
证法1:在边形内任取一点,并把这点与各个顶点连接起来,共构成个三角形,这个三角形的内角和为,再减去一个周角,即得到边形的内角和为.
证法2:从边形一个顶点作对角线,可以作条对角线,并且边形被分成个三角形,这个三角形内角和恰好是边形的内角和,等于.
证法3:在边形的一边上取一点与各个顶点相连,得个三角形,边形内角和等于这个三角形的内角和减去所取的一点处的一个平角的度数,
即.
要点诠释:
(1)注意:以上各推导方法体现出将多边形问题转化为三角形问题来解决的基础思想。
(2)内角和定理的应用:
①已知多边形的边数,求其内角和;
②已知多边形内角和,求其边数。
知识点五:多边形的外角和公式
1.公式:多边形的外角和等于360°.
2.多边形外角和公式的证明:多边形的每个内角和与它相邻的外角都是邻补角,所以边形的内角和加外角和为,外角和等于.注意:n边形的外角和恒等于360°,它与边数的多少无关。
要点诠释:
(1)外角和公式的应用:
①已知外角度数,求正多边形边数;
②已知正多边形边数,求外角度数.
(2)多边形的边数与内角和、外角和的关系:
①n边形的内角和等于(n-2)·180°(n≥3,n是正整数),可见多边形内角和与边数n有关,每增加
1条边,内角和增加180°。
②多边形的外角和等于360°,与边数的多少无关。
知识点六:镶嵌的概念和特征
1、定义:用一些不重叠摆放的多边形把平面的一部分完全覆盖,通常把这类问题叫做用多边形覆盖平面(或平面镶嵌)。这里的多边形可以形状相同,也可以形状不相同。
2、实现镶嵌的条件:拼接在同一点的各个角的和恰好等于360°;相邻的多边形有公共边。
3、常见的一些正多边形的镶嵌问题:
(1)用正多边形实现镶嵌的条件:边长相等;顶点公用;在一个顶点处各正多边形的内角之和为360°。
(2)只用一种正多边形镶嵌地面
对于给定的某种正多边形,怎样判断它能否拼成一个平面图形,且不留一点空隙?解决问题的关键在于正多边形的内角特点。当围绕一点拼在一起的几个正多边形的内角加在一起恰好组成一个周角360°时,就能铺成一个平面图形。
事实上,正n边形的每一个内角为,要求k个正n边形各有一个内角拼于一点,恰好覆盖地面,这样360°=,由此导出k==2+,而k是正整数,所以n只能取3,4,6。因而,用相同的正多边形地砖铺地面,只有正三角形、正方形、正六边形的地砖可以用。
注意:任意四边形的内角和都等于360°。所以用一批形状、大小完全相同但不规则的四边形地砖也可以铺成无空隙的地板,用任意相同的三角形也可以铺满地面。
(3)用两种或两种以上的正多边形镶嵌地面
用两种或两种以上边长相等的正多边形组合成平面图形,关键是相关正多边形“交接处各角之和能否拼成一个周角”的问题。例如,用正三角形与正方形、正三角形与正六边形、正三角形与正十二边形、正四边形与正八边形都可以作平面镶嵌,见下图:
又如,用一个正三角形、两个正方形、一个正六边形结合在一起恰好能够铺满地面,因为它们的交接处各角之和恰好为一个周角360°。
规律方法指导
1.内角和与边数成正比:边数增加,内角和增加;边数减少,内角和减少. 每增加一条边,内角的和
就增加180°(反过来也成立),且多边形的内角和必须是180°的整数倍.
2.多边形外角和恒等于360°,与边数的多少无关.
3.多边形最多有三个内角为锐角,最少没有锐角(如矩形);多边形的外角中最多有三个钝角,最少
没有钝角.
4.在运用多边形的内角和公式与外角的性质求值时,常与方程思想相结合,运用方程思想是解决本节
问题的常用方法.
5.在解决多边形的内角和问题时,通常转化为与三角形相关的角来解决. 三角形是一种基本图形,是
研究复杂图形的基础,同时注意转化思想在数学中的应用.
经典例题透析
类型一:多边形内角和及外角和定理应用
1.一个多边形的内角和等于它的外角和的5倍,它是几边形?
思路点拨:本题实际告诉了这个多边形的内角和是.
解析:设这个多边形是边形,
则它的内角和是,
所以,解得.
所以这个多边形是十二边形.
总结升华:本题是多边形的内角和定理和外角和定理的综合运用. 只要设出边数,根据条件列出关于的方程,求出的值即可,这是一种常用的解题思路.
举一反三:
【变式1】若一个多边形的内角和与外角和的总度数为1800°,求这个多边形的边数.
【答案】设这个多边形的边数为,根据题意得:
,
解得.
所以多边形的边数为10.
【变式2】一个多边形除了一个内角外,其余各内角和为2750°,求这个多边形的内角和是多少?
【答案】设这个多边形的边数为,这个内角为,
则,
即.
因为等式左边是180°的整数倍,所以等式右边也是180°的整数倍.
又因为,
所以,此时.
所以这个多边形的内角和是:.
【变式3】个多边形的内角和与某一个外角的度数总和为1350°,求这个多边形的边数。
【答案】可设多边形的边数为n,某一个外角为α
则(n-2)×180+α=1350
从而(n-2)=
因为边数n为正整数,所以α=90,n=9
类型二:多边形对角线公式的运用
2.某校七年级六班举行篮球比赛,比赛采用单循环积分制(即每两个班都进行一次比赛).你能算出一共需要进行多少场比赛吗?
思路点拨:本题体现与体育学科的综合,解题方法参照多边形对角线条数的求法,即多边形的对角线条数加上边数. 如图:
解析:共需要比赛(场).
所以一共需要进行15场比赛.
总结升华:对于其他学科问题要善于把它与数学知识联系在一起,便于解决.
举一反三:
【变式1】一个多边形共有20条对角线,则多边形的边数是( ).
A.6 B.7 C.8 D.9
【答案】C. 提示:一个多边形的对角线条数为条,将6、7、8、9分别代入,结果为20的即为正确答案.
【变式2】一个十二边形有几条对角线。
解析:过十二边形的任意一个顶点可以画9条对角线,那么十二个顶点可以画12×9条对角线,
但每条对角线在每个顶点都数了一次,所以实际对角线的条数应该为12×9÷2=54(条)
∴十二边形的对角线共有54条。
总结升华:对于一个n边形的对角线的条数,我们可以总结出规律条,牢记这个公式,以后只要用相应的n的值代入即可求出对角线的条数,要记住这个公式只有在理解的基础之上才能记得牢。
类型三:可转化为多边形内角和问题
3.如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.
思路点拨: 设法将这几个角转移到一个多边形中,然后利用多边形内角和公式求解.
解析:连接BF,则∠A+∠G=∠1+∠2.
∴∠A+∠ABC+∠C+∠D+∠E+∠EFG+∠G
=∠1+∠2+∠ABC+∠C+∠D+∠E+∠EFG.
=(5-2) ·180°= 540°.
总结升华:本题通过作辅助线,把∠A与∠G的和转化为∠1与∠2的和,从而把问题变为求五边形的内角和运算,“转化思想”是解决本题的关键.
举一反三:
【变式1】如图所示,∠1+∠2+∠3+∠4+∠5+∠6=__________.
【答案】360°.(提示:把∠1、∠2、∠3、∠4、∠5、∠6转移到同一个多边形内.)
【变式2】如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数。
解析:连结ED,在ΔAOB和ΔDOE中,
∵∠AOB=∠DOE,
∴∠1+∠2=∠A+∠B
∴∠A+∠B+∠C+∠CDO+∠OEF+∠F
=∠2+∠1+∠C+∠CDO+∠OEF+∠F
=∠C+∠CDE+∠DEF+∠F=360°
类型四:实际应用题
4.如图,一辆小汽车从P市出发,先到B市,再到C市,再到A市,最后返回P市,这辆小汽车共转了多少度角?
思路点拨:根据多边形的外角和定理解决.
解析:如图,
当小汽车从P出发行驶到B市,由B市向C市行驶时转的角是,由C市向A市行驶时转的角是,
由A市向P市行驶时转的角是.
因此,小汽车从P市出发,经B市、C 市、A市,又回到P市,共转.
总结升华:旋转的角度是指原来前进的方向与转弯后的方向的夹角.小汽车沿任意多边形行驶一周回到原处,转过的角度都是360°。
举一反三:
【变式1】如图所示,小亮从A点出发前进10m,向右转15°,再前进10m,又向右转15°,…,这样一直走下去,当他第一次回到出发点时,一共走了__________m.
【答案】240. 提示:小亮每次向右转的角度相同,并且前进的路程也相同,因此当他第一次回到出发点A时,所走的路程是一个正多边形的周长,每次转的角度是这个正多边形的一个外角,所以这个正多边形的边数是360°÷15°=24,所以小亮一共走了10×24=240(m)
【变式2】小华从点A出发向前走10米,向右转36°,然后继续向前走10米,再向右转36°,他以同样的方法继续走下去,他能回到点A吗?若能,当他走回点A时共走了多少米?若不能,写出理由。
解析:可以走回到A点,共走100米,理由,根据多边形的外角和是360°可知,每次向右转36°,
并且都走10米,可得,小华共转10次,故共走100米。
所以,可以走回到A点,共走100米。
【变式3】如图所示是某厂生产的一块模板,已知该模板的边AB∥CF,CD∥AE. 按规定AB、CD的延长线相交成80°角,因交点不在模板上,不便测量. 这时师傅告诉徒弟只需测一个角,便知道AB、CD的延长线的夹角是否合乎规定,你知道需测哪一个角吗?说明理由.
思路点拨:本题中将AB、CD延长后会得到一个五边形,根据五边形内角和为540°,又由AB∥CF,CD∥AE,可知∠BAE+∠AEF+∠EFC=360°,从540°中减去80°再减去360°,剩下∠C的度数为100°,所以只需测∠C的度数即可,同理还可直接测∠A的度数.
解析:测∠A或∠C的度数,只需∠A=100°或∠C=100°,
即知模板中AB、CD的延长线的夹角是否符合规定.
理由如下:连接AF,∵AB∥CF,
∴∠BAF+∠AFC=180°.
又∵∠EAF+∠E+∠AFE=180°,
∴∠BAE+∠E+∠EFC=360°.
若∠C=100°,
则AB、CD的延长线的夹角=540°- 360°- 100°= 80°,
即符合规定.
同理:若连接CE,可得∠AEF+∠F+∠DCF=360°.
若∠A=100°,则也符合规定.
总结升华:本题实际上是多边形内角和的逆运算,关键在于正确添加辅助线.
类型五:镶嵌问题
5.分别画出用相同边长的下列正多边形组合铺满地面的设计图。
(1)正方形和正八边形;
(2)正三角形和正十二边形;
(3)正三角形、正方形和正六边形。
思路点拨:只要在拼接处各多边形的内角的和能构成一个周角,那么这些多边形就能作平面镶嵌。
解析:正三角形、正方形、正六边形、正八边形、正十二边形的每一个内角分别是60°、90°、120°、135°、150°。
(1)因为90+2×135=360,所以一个顶点处有1个正方形、2个正八边形,如图(1)所示。
(2)因为60+2×150=360,所以一个顶点处有1个正三角形、2个正十二边形,如图(2)所示。
(3)因为60+2×90+120=360,所以一个顶点处有1个正三角形、1个正六边形和2个正方形,如图(3)
所示。
总结升华:用两种以上边长相等的正多边形组合成平面图形,实质上是相关正多边形“交接处各角之和能否拼成一个周角”的问题。
举一反三:
【变式1】分别用形状、大小完全相同的①三角形木板;②四边形木板;③正五边形木板;④正六边形木板作平面镶嵌,其中不能镶嵌成地板的是( )
A、① B、② C、③ D、④
【答案】C
解析:用同一种多边形木板铺地面,只有正三角形、四边形、正六边形的木板可以用,不能用正五边形木板,故选C。
【变式2】用三块正多边形的木板铺地,拼在一起并相交于一点的各边完全吻合,其中两块木板的边数都是8,则第三块木板的边数应是( )
A、4 B、5 C、6 D、8
【答案】A (提示:先算出正八边形一个内角的度数,再乘以2,然后用360°减去刚才得到的积,便得到第三块木板一个内角的度数,进而得到第三块木板的边数)
【变式3】(2010内蒙古赤峰)下面平面图形中,不能镶嵌平面的图形是 ( )
A.任意一个三角形 B.任意一个四边形
C.任意一个正五边形 D.任意一个正六边形
【答案】C
解析:把两个三角形的6个内角放在一处,恰好是360°;四边形的内角和为360°,能够镶嵌平面;正六边形每一个内角是120°,120是360的约数,也能够镶嵌平面;正五边形的每一个内角是108°,108不是360的约数,不能镶嵌平面.
学习成果测评
基础达标:
选择题
1.多边形的内角和不可能是( ).
A.1800° B.540° C.800° D.360°
2.一个多边形的内角中,锐角的个数最多有( ).
A.3个 B.4个 C.5个 D.6个
3.四边形中,如果有一组对角都是直角,那么另一组对角可能( ).
A.都是钝角; B.都是锐角
C.是一个锐角、一个钝角 D.是一个锐角、一个直角
4.若从一个多边形的一个顶点出发,最多可以引10条对角线,则它是( ).
A.十三边形 B.十二边形 C.十一边形 D.十边形
5.如图,国旗上的五角星的五个角的度数是相同的,每一个角的度数都是( ).
A.30° B.35° C.36° D.42°
6.如图,∠A+∠B+∠C+∠D+∠E+∠F=( ).
A.180° B.360° C.540° D.720°
7.如图,至少去掉( )个点,才能使留下的任何三个点都不能组成一个正三角形( ).
A.2 B.3 C.4 D.5
8.从一个边形中除去一个角后,其余个内角和是2580°,则原多边形的边数是( ).
A.15 B.17 C.19 D.13
9.(2010广东肇庆)一个多边形的内角和是外角和的2倍,则这个多边形是 ( )
A.四边形 B.五边形 C.六边形 D.八边形
10.(2010福建泉州)如图所示,在折纸活动中,小明制作了一张△ABC纸片,点D、E分别在边AB、AC
上,将△ABC沿着DE折叠压平,A与重合,若∠A=70°,则∠1+∠2= ( )
A.140° B.130° C.110° D.70°
填空题
11.如果一个多边形的每一个内角都相等,且每一个内角都大于135°, 那么这个多边形的边数最少为__.
12.已知一个多边形的每一个外角都相等,一个内角与一个外角的度数之比为9:2,则这个多边形的边数
为_______.
13.一个多边形,每个内角的度数都比它相邻的外角度数的2倍多45°,则它是_______边形.
14.(为整数,且)边形的内角和比边形的内角和小_________度.
15.一个多边形的每一个外角的度数等于与其相邻内角的度数的,则这个多边形是___________边形.
16.如图所示,一个顶角为40°的等腰三角形纸片,剪去一个顶角后,得到一个四边形,则
∠1+∠2=___________.
17.一个多边形的每个内角都等于120°,则从此多边形一个顶点出发引出___________条对角线.
18.小勇制造了一个简单的机器人,小勇遥控它每前行1m就向左转30°,再向前行1m又向左转30°,问
它需要走___________m才能走回原地.
解答题
19.凸边形的个内角与某一个外角的总和为1450°,则的值是多少?
20.四个村庄地理位置如图,点A、B、C、D处,为了解决四个村庄饮水问题,现准备兴建一座地下水供水厂,问建在何处,材料费用最低,画出示意图,并说明理由.
能力提升
1.如图所示,用火柴杆摆出一系列三角形图案,按这种方式摆下去,当摆到20层()时,需要多少根火柴
2.如图所示,某厂规定一块模板中AB、CD的延长线相交成80°角,因交点不在板上,不便测量,工人师傅连接AC,测得∠BAC=34°,∠DCA=65°,此时AB、CD的延长线相交的角是否符合规定?为什么?
3.将一块正六边形硬纸片如图(1),做成一个底面仍为正六边形且高相等的无盖纸盒(侧面均垂直于底面,如图(2),需要在每一个顶点处减去一个四边形,如图(1)中的四边形AGA′H,求∠GA′H的大小.
(1) (2)
4.(开放性问题)一个长方形被截掉一个角后,得到一个多边形,此多边形的内角和是多少度?
综合探究:
1.如图所示,求∠A+∠B+∠C+∠D+∠E+∠F的度数.
2.已知六边形ABCDEF,如图,它的每个内角都相等,且AB=1,BC=CD=DE=9,求这个六边形的周长.
答案与解析
基础达标:
选择题
1.C.
提示:根据多边形内角和定理,可知,内角和一定是180°的整数倍,故其不可能为多边
形的内角和.
2.A.
3.C.
4.A.
5.C.
提示:将五角星的五个角转移到一个三角形中,由三角形内角和定理以及五角星的各个角都相等,
即可求出各个角的度数.
6.B.
提示:∠A+∠B、∠C+∠D、∠E+∠F转移到中间三角形的外角位置上.
7.C.
8.B.
提示:设除去的内角为,则,即,
又∵为整数,∴,.
9.C.
提示:已知任意多边形的外角和是360°,可以知道其内角和是720°.
利用内角和公式可知这个多边形是一个六边形.
10.A.
提示:由∠A=70°得∠AED+∠ADE=110°,再由折叠可知,
故
填空题
11.9.
12.11.
13.八.
提示:由于外角和度数为360°,则可设出边数,
再根据内角和公式列方程解题. 设边数为,
则有,解得.
14.180°.
提示:.
15.八.
提示:设每个外角为,则,
解得,而多边形边数.
16.220°.
提示:由顶角为40°可知两底角和为140°,
∴∠1+∠2=360°-140°=220°.
此题考察三角形、四边形的内角和定理.
17.3.
18.12.
提示:机器人走过了一个外角为30°的正多边形,由任意多边形的外角和均为360°,
所以有,得,所以它需要走12m才能走回原地.
解答题
19.解:设这个外角为,则有,
因为为整数,所以解得,.
20.连结AC、BD交于点O,则点O就是要求的点.
能力提升
1.630根.
提示:实际摆放层数和增加的三角形的数量是一样的,
所以在第20层时,一共有1+2+…+20个三角形.
2.解:不符合规定,因为AB、CD的延长线相交成的角为81°.
3.60°.
提示:四边形AGA′H中,边A′H与A′G一定与正六边形各边垂直,
又由正六边形一个内角为120°,可得∠GA′H的大小为60°.
4.提示:本题是开放性问题,应分情况进行讨论,要注意长方形去掉一个角后所有可能情况.
解:长方形去掉一个角后得到的多边形有3种情况,如图:
它们分别是三角形、四边形、五边形,所以内角和分别为180°、360°、 540°.
综合探究
1.解:如图,
∵∠3=360°-∠D-∠E-∠F,
∴∠1=180°-∠3=180°-(360°-∠D-∠E-∠F)
=∠D+∠E+∠F-180°.
又∵∠2=∠B+∠C,
∴∠A+∠1+∠2=∠A+∠D+∠E+∠F-180°+∠B+∠C=180°,
即∠A+∠B+∠C+∠D+∠E+∠F=360°.
2.解:如图所示,
延长AB、DC交于G,延长CD、FE交于H,延长BA、EF交于L.
由六边形的每个内角都相等知,
它的每个外角都等于.
∴△CBG、△DHE、△AFL和△GHL都是等边三角形,
∴GH=GC+CD+DH=BC+CD+DE=27,GL=27,
即GB+AB+AL=BC+AB+AF=27,∴9+1+AF=27,
∴AF=17.
同理,由LH=27,即LF+FE+EH=27,得EF=1.
∴六边形ABCDEF的周长为1+9×3+1+17=46.
