七年级数学三角形的内角
图片预览




文档简介
(共18张PPT)
人教版数学教材七年级下
7.2 与三角形有关的角(1)
三角形的内角
大家都已经知道三角形的三个内角和为180度,你能证明吗?
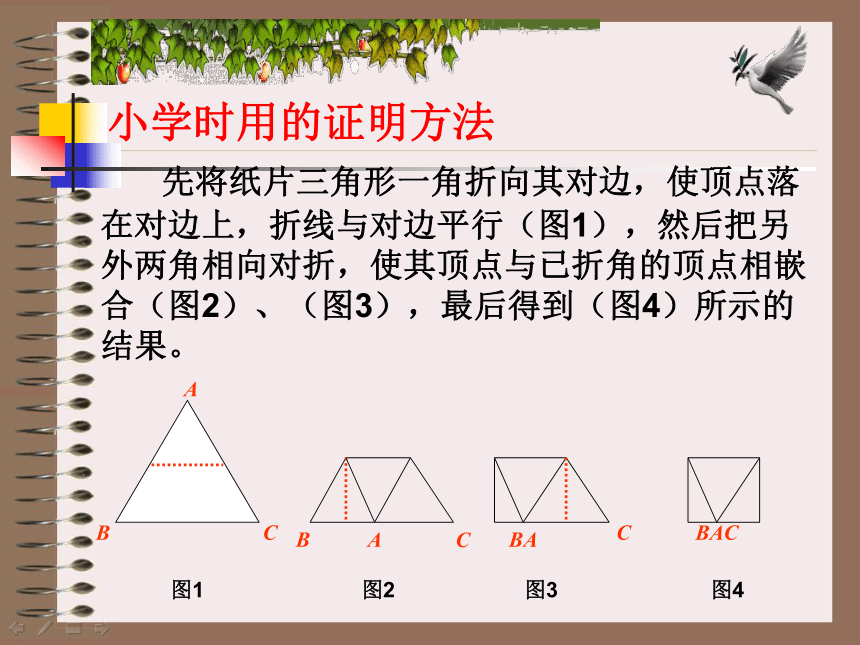
先将纸片三角形一角折向其对边,使顶点落在对边上,折线与对边平行(图1),然后把另外两角相向对折,使其顶点与已折角的顶点相嵌合(图2)、(图3),最后得到(图4)所示的结果。
A
C
B
图1
B
A
C
图2
BA
C
图3
BAC
图4
小学时用的证明方法
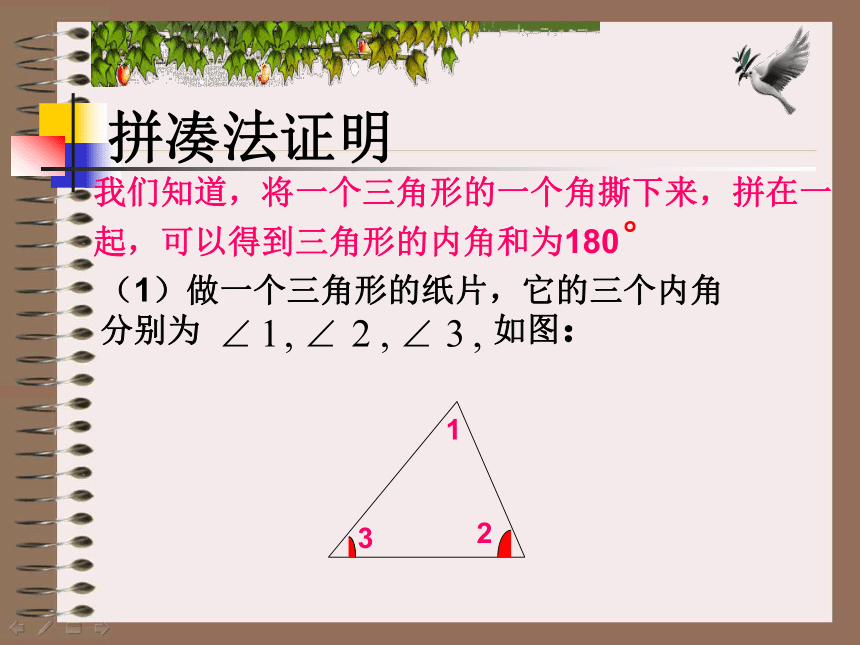
我们知道,将一个三角形的一个角撕下来,拼在一起,可以得到三角形的内角和为180°
(1)做一个三角形的纸片,它的三个内角
分别为
如图:
1
2
3
拼凑法证明
(2)将∠1撕下,如图,其中∠1的顶点与∠2的顶点重合,它的一条边与∠2的一条边重合,∠1的另一条边b与∠3的一条边a平行吗?Why
1
2
3
1
a
b
拼凑法证明
∠ 3与∠ 4的大小有什么关系?为什么?
(3)如图,将∠ 3与∠ 2的公共边延长,它与b所夹的角为∠ 4。
拼凑法证明
1
2
3
1
a
b
4
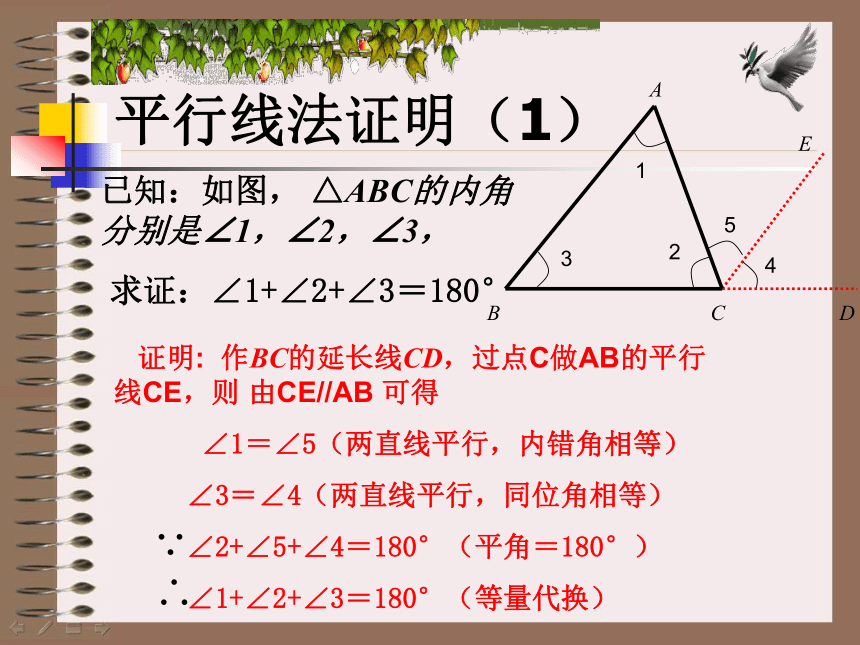
已知:如图, △ABC的内角分别是∠1,∠2,∠3,
求证:∠1+∠2+∠3=180°
证明: 作BC的延长线CD,过点C做AB的平行线CE,则 由CE//AB 可得
∠1=∠5(两直线平行,内错角相等)
∠3=∠4(两直线平行,同位角相等)
∠2+∠5+∠4=180°(平角=180°)
∠1+∠2+∠3=180°(等量代换)
A
B
C
5
4
D
E
2
3
1
平行线法证明(1)
A
B
C
Q
P
在证明三角形内角和定理时,小明的想法是把三个角“凑”到A处,他过点A作直线PQ//BC,他的想法可行吗?
3
2
1
证明: 过点A作PQ//BC,则
∠2=∠B(两直线平行,内错角相等)
∠3=∠C(两直线平行,内错角相等)
∠1+∠2+∠3=180°(一平角=180°)
∠1+∠B +∠C=180°(等量代换)
平行线法证明(2)
经典例题
C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西 40°方向,从C岛看A、B两岛的视角∠ACB 是多少度?
分析:A、B、C三岛的连线构成△ABC,所求的是△ ABC的一个内角.如果能求出∠CAB、 ∠ABC,就能求出∠ACB.
解:
D
A
B
E
C
北
答:从C岛看A、B两岛的视角∠ACB 是90°.
D
A
B
E
C
北
还有其他解法吗?
经典例题
猜一猜
(1)下图中小明所拿三角形被遮住的两个内角是什么角?小颖的呢?试着说明理由.
下图中三角形被遮住的两个内角可能是什么角 将所得结果与(1)的结果进行比较.
猜一猜
按三角形内角的大小分类
三角形的分类
锐角三角形
三个内角都是锐角
钝角三角形
有一个内角是钝角
直角三角形
有一个内角是直角
注意:1.常用符号“Rt ABC”来表示直角三角形ABC.
直角边
直角边
斜边
2.把直角所对的边称为直角三角形的斜边,
夹直角的两条边称为直角边.
3.直角三角形的两个锐角互余.
A
B
C
对号入座
锐角三角形
直角三角形
钝角三角形
⑦
②
①
③
④
⑤
⑥
学习了本节课你有哪些 收获?
B
A
D
C
1、从A处观测C处的仰角∠CAB =30°,从B处观测C处时仰角∠CB D=45°,从C处观测A、B两处时的视角∠ACB 是多少度?
练 习
2、证明:四边形的内角和
为360o.
3、如图,一种滑翔伞的形
状是左右对称的四边形ABCD,其中∠A =150°, ∠B = ∠D= 40°, 求∠C的度数.
B
A
C
D
40°
150°
40°
作 业
人教版数学教材七年级下
7.2 与三角形有关的角(1)
三角形的内角
大家都已经知道三角形的三个内角和为180度,你能证明吗?
先将纸片三角形一角折向其对边,使顶点落在对边上,折线与对边平行(图1),然后把另外两角相向对折,使其顶点与已折角的顶点相嵌合(图2)、(图3),最后得到(图4)所示的结果。
A
C
B
图1
B
A
C
图2
BA
C
图3
BAC
图4
小学时用的证明方法
我们知道,将一个三角形的一个角撕下来,拼在一起,可以得到三角形的内角和为180°
(1)做一个三角形的纸片,它的三个内角
分别为
如图:
1
2
3
拼凑法证明
(2)将∠1撕下,如图,其中∠1的顶点与∠2的顶点重合,它的一条边与∠2的一条边重合,∠1的另一条边b与∠3的一条边a平行吗?Why
1
2
3
1
a
b
拼凑法证明
∠ 3与∠ 4的大小有什么关系?为什么?
(3)如图,将∠ 3与∠ 2的公共边延长,它与b所夹的角为∠ 4。
拼凑法证明
1
2
3
1
a
b
4
已知:如图, △ABC的内角分别是∠1,∠2,∠3,
求证:∠1+∠2+∠3=180°
证明: 作BC的延长线CD,过点C做AB的平行线CE,则 由CE//AB 可得
∠1=∠5(两直线平行,内错角相等)
∠3=∠4(两直线平行,同位角相等)
∠2+∠5+∠4=180°(平角=180°)
∠1+∠2+∠3=180°(等量代换)
A
B
C
5
4
D
E
2
3
1
平行线法证明(1)
A
B
C
Q
P
在证明三角形内角和定理时,小明的想法是把三个角“凑”到A处,他过点A作直线PQ//BC,他的想法可行吗?
3
2
1
证明: 过点A作PQ//BC,则
∠2=∠B(两直线平行,内错角相等)
∠3=∠C(两直线平行,内错角相等)
∠1+∠2+∠3=180°(一平角=180°)
∠1+∠B +∠C=180°(等量代换)
平行线法证明(2)
经典例题
C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80°方向,C岛在B岛的北偏西 40°方向,从C岛看A、B两岛的视角∠ACB 是多少度?
分析:A、B、C三岛的连线构成△ABC,所求的是△ ABC的一个内角.如果能求出∠CAB、 ∠ABC,就能求出∠ACB.
解:
D
A
B
E
C
北
答:从C岛看A、B两岛的视角∠ACB 是90°.
D
A
B
E
C
北
还有其他解法吗?
经典例题
猜一猜
(1)下图中小明所拿三角形被遮住的两个内角是什么角?小颖的呢?试着说明理由.
下图中三角形被遮住的两个内角可能是什么角 将所得结果与(1)的结果进行比较.
猜一猜
按三角形内角的大小分类
三角形的分类
锐角三角形
三个内角都是锐角
钝角三角形
有一个内角是钝角
直角三角形
有一个内角是直角
注意:1.常用符号“Rt ABC”来表示直角三角形ABC.
直角边
直角边
斜边
2.把直角所对的边称为直角三角形的斜边,
夹直角的两条边称为直角边.
3.直角三角形的两个锐角互余.
A
B
C
对号入座
锐角三角形
直角三角形
钝角三角形
⑦
②
①
③
④
⑤
⑥
学习了本节课你有哪些 收获?
B
A
D
C
1、从A处观测C处的仰角∠CAB =30°,从B处观测C处时仰角∠CB D=45°,从C处观测A、B两处时的视角∠ACB 是多少度?
练 习
2、证明:四边形的内角和
为360o.
3、如图,一种滑翔伞的形
状是左右对称的四边形ABCD,其中∠A =150°, ∠B = ∠D= 40°, 求∠C的度数.
B
A
C
D
40°
150°
40°
作 业
