六年级数学下册试题 一课一练《图形与几何-图形的运动》 人教版(含答案)
文档属性
| 名称 | 六年级数学下册试题 一课一练《图形与几何-图形的运动》 人教版(含答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 690.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 10:30:37 | ||
图片预览


文档简介
《图形与几何-图形的运动》
一、填空题
1.下列现象,哪些是“平移”,哪些是“旋转”?分别填在括号里.
(1)张叔叔在笔直的公路上开车,方向盘的运动是
现象.
(2)升国旗时,国旗的升降运动是
现象.
(3)自行车的车轮转了一圈又一圈是
现象.
(4)妈妈用拖布擦地,是
现象.
2.边长4cm的正方形按2:1放大,得到的图形的面积是
cm2.
3.在横线上填“平移”或“旋转”.
(1)一辆汽车在一段笔直高速公路上行驶,这时车身的运动是
,车轮的运动是
.
(2)钟面上分钟的运动是
,秒钟的运动是
.
4.从4:15到4:30,分针将会按
时针方向旋转
°.
5.下面哪些图形是轴对称图形?请在括号中打“√”.
6.把长方形的每条边放大到原来的5倍,放大后的长方形与原来长方形对应边长的比是
;把底9厘米、高6厘米的三角形按1:3的比缩小后,三角形的底是
厘米,高是
厘米.
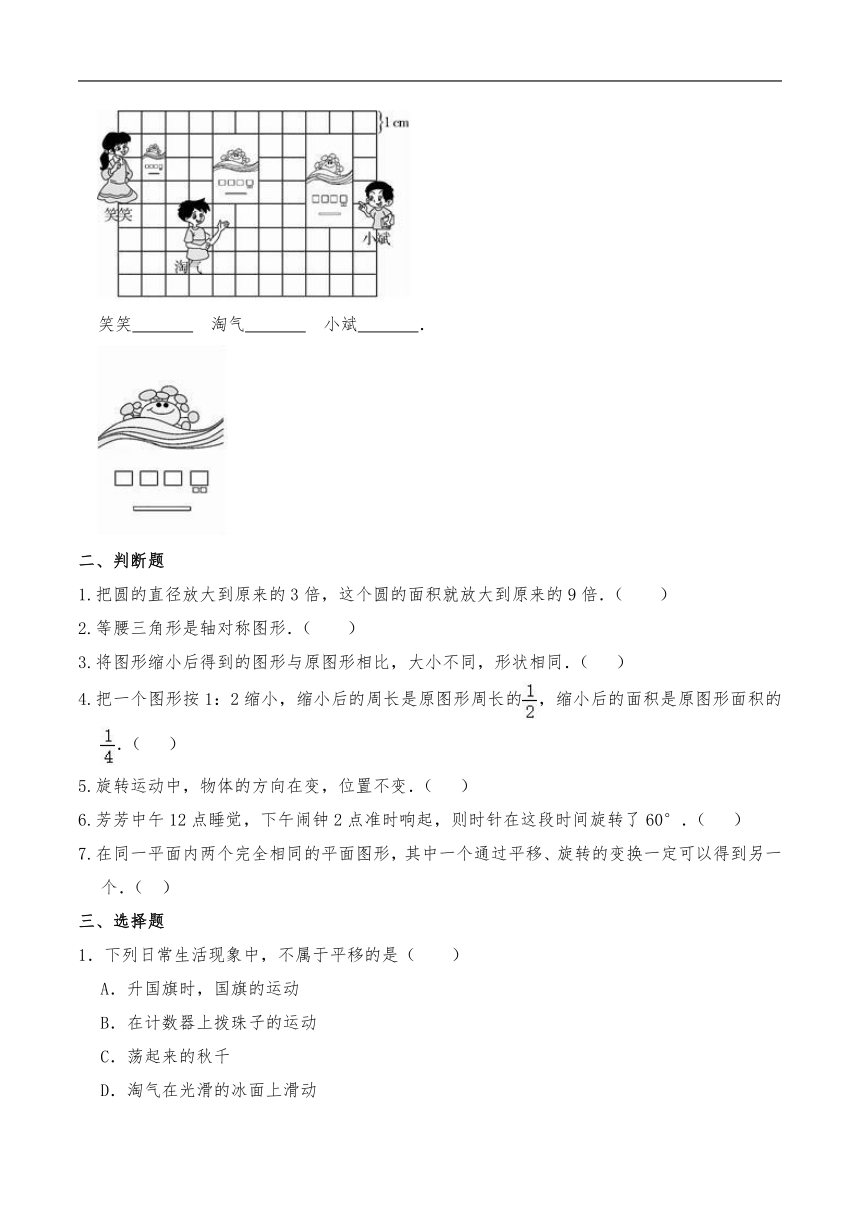
7.一张贺卡的长是6cm,宽是4cm,下面是三位小朋友画在方格纸上的贺卡示意图,谁画得像?在横线里画“√”.
笑笑
淘气
小斌
.
二、判断题
1.把圆的直径放大到原来的3倍,这个圆的面积就放大到原来的9倍.(
)
2.等腰三角形是轴对称图形.(
)
3.将图形缩小后得到的图形与原图形相比,大小不同,形状相同.(
)
4.把一个图形按1:2缩小,缩小后的周长是原图形周长的,缩小后的面积是原图形面积的.(
)
5.旋转运动中,物体的方向在变,位置不变.(
)
6.芳芳中午12点睡觉,下午闹钟2点准时响起,则时针在这段时间旋转了60°.(
)
7.在同一平面内两个完全相同的平面图形,其中一个通过平移、旋转的变换一定可以得到另一个.(
)
三、选择题
1.下列日常生活现象中,不属于平移的是( )
A.升国旗时,国旗的运动
B.在计数器上拨珠子的运动
C.荡起来的秋千
D.淘气在光滑的冰面上滑动
2.下面的哪组图形经过平移能够互相重合?( )
A.
B.
C.
3.有无数条对称轴的图形是( )
A.长方形
B.正方形
C.等边三角形
D.圆形
4.把一个正方形的各边按1:3缩小后,现在的图形和原来图形的面积比是( )
A.1:3
B.3:1
C.1:9
5.下面说法正确的是( )
A.旋转改变图形的形状和大小
B.平移改变图形的形状和大小
C.平移和旋转都不改变图形的形状和大小
6.下列图形中,对称轴最多的是( )
A.长方形
B.平行四边形
C.等边三角形
D.圆
7.一个三角形是轴对称图形,这个三角形一定是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
8.下列图形中对称轴最多的是( )
A.圆形
B.正方形
C.长方形
四.计算题
1.将图1的三角形按比例缩小后得到图2的三角形,求未知数x.
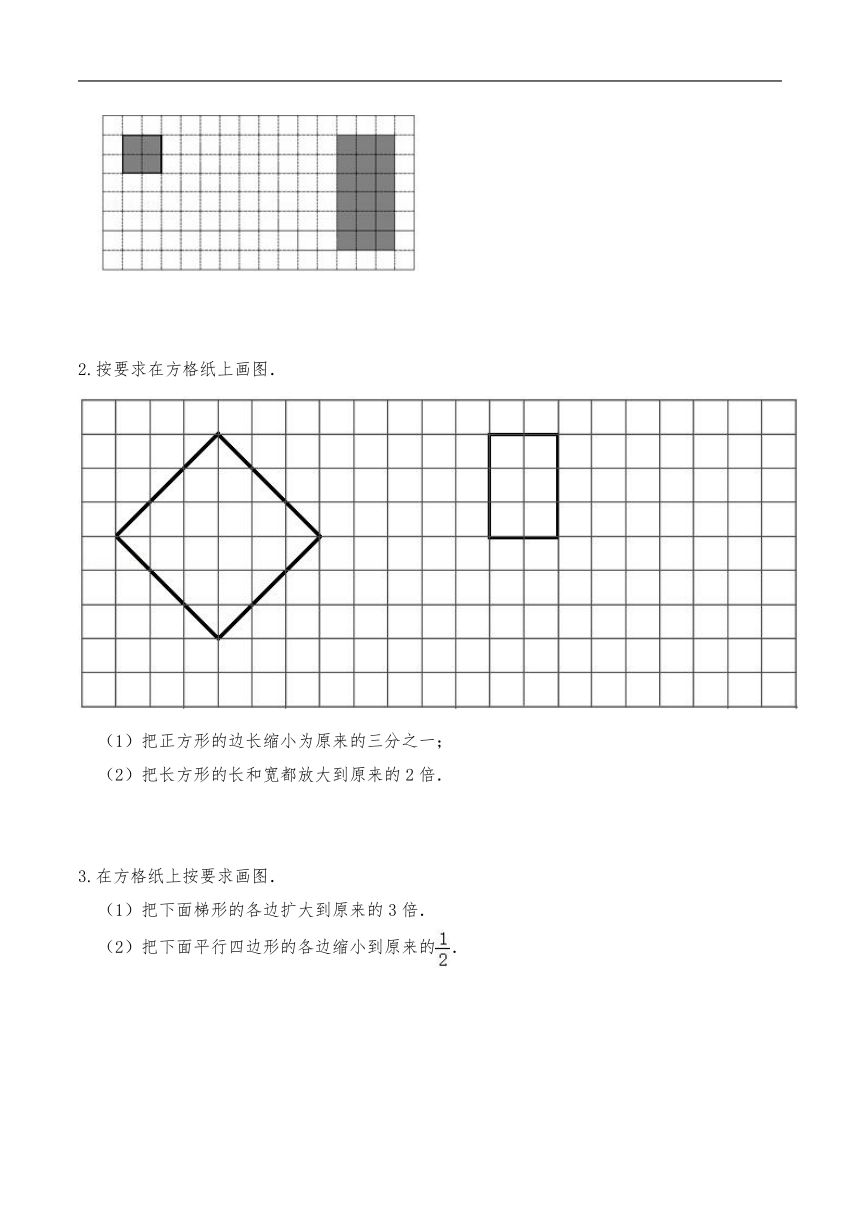
2.画出图形A按2:1放大后的图形C;画出图形B按1:2缩小后的图形D.
五、应用题
1.一个正方形放大后的边长是9厘米,放大后的面积是原来的9倍.这个正方形原来的边长是多少厘米?
2.小明在电脑上把一张长方形图片按比例放大后如图,放大后的宽是多少厘米?
六、操作题
1.画一画:把正方形各边放大到原来的2倍,把长方形各边缩小为原来的.
2.按要求在方格纸上画图.
(1)把正方形的边长缩小为原来的三分之一;
(2)把长方形的长和宽都放大到原来的2倍.
3.在方格纸上按要求画图.
(1)把下面梯形的各边扩大到原来的3倍.
(2)把下面平行四边形的各边缩小到原来的.
4.
(1)按照2:1的比画出三角形放大后的图形,新图形面积是原来面积的
倍.
(2)画出三角形绕A点逆时针方向旋转90°后的图形,旋转后B点的位置是(
,
).
(3)画一个平行四边形,面积与放大后的三角形面积相等.
(4)涂色的正方形与大正方形的面积比是
.
5.按1:2的比在图中画出三角形A缩小后的图形B,再画出和三角形A面积相等的平行四边形C和梯形D各一个.
6.操作题
(1)画出图①的另一半,使它成为一个轴对称图形.
(2)画出将图②绕A点顺时针旋转90°后的图形.
(3)图中圆的圆心位置用数对表示是(
,
).画出将圆先向右平移7格再向下平移2格后的图形.画出将圆按3:1的比放大后的图形,放大后面积与原来面积之比是
.
7.(1)把图中的长方形按1:2的比例缩小后的图形在网格线上画出来.
(2)把图中的梯形按2:1的比例放大后的图形在网格线上画出来.
(3)计算放大后的梯形的面积(1格长按1cm计算).
七、解答题
1.用4个相同的小正方形可以拼成下面几种图形.
(1)上面四个图形中,是轴对称图形的有
和
,(填序号)
(2)在不是轴对称图形的图形上,再添上一个小正方形,使它成为轴对称图形.
(3)画出上图中三角形先向南移动3格再向西移动2格后的图形,
2.按要求画一画.(每个小正方形的边长是1厘米)
(1)按2:1画出如图中正方形放大后的图形,在放大后的正方形里画一个最大的圆,并画出这个图形的对称轴.
(2)画出梯形绕点O按逆时针旋转90°后的图形,此时点A用数对表示是(
,
).
3.按要求在如图方格纸上画图.
①把图形绕点O顺时针旋转90度,得到图形B.
②把图形B向右平移4格得到图形C.
4.把图中的平行四边形先按2:1的比放大,画出放大后的图形,再绕A点顺时针旋转90°,画出旋转后的图形.
5.按要求在下面方格纸上画图.
(1)将下面的梯形按2:1放大.
(2)画出三角形ABC先向下平移4格,再向右平移3格后的图形.
(3)将三角形ABC绕C点顺时针方向旋转90°,画出旋转后的图形.
6.这些现象哪些是“平移”现象,哪些是“旋转”现象:
(1)张叔叔在笔直的公路上开车,方向盘的运动是
现象.
(2)升国旗时,国旗的升降运动是
现象.
(3)妈妈用拖布擦地,是
现象.
(4)自行车的车轮转了一圈又一圈是
现象.
答案
一、填空题
1.旋转,平移,旋转,平移.
2.64.
3.平移,旋转,旋转,旋转.
4.顺,90.
5.解:在平面图形中,长方形、正方形、圆、扇形、等腰三角形、等腰梯形都是轴对称图形.
6.5:1,3,2.
7.×,√,×.
二、判断题
1.√.2.√.3.√.4.√.5.×.6.√.7.×.
三、选择题
1.C.2.B.3.D.4.C.5.C.6.D.7.D.8.A.
四、计算题
1.解:设未知边为x,
1.6:x=3.2:4.8
3.2
x=1.6×4.8
x=2.4
答:未知数为2.4.
2.解:画出图形A按2:1放大后的图形C(下图红色部分);画出图形B按1:2缩小后的图形D(下图绿色部分):
五、应用题
1.解:因为这个正方形放大后面积是原来的9倍
所以这个正方形扩大了3倍
9÷3=3(厘米)
答:这个正方形原来的边长是3厘米.
2.解:18÷3=6
2×6=12(cm)
答:放大后的宽是12厘米.
六、操作题
1.解:把正方形各边放大到原来的2倍,把长方形各边缩小为原来的.
如图所示:
2.解:(1)把正方形的边长缩小为原来的三分之一;
(2)把长方形的长和宽都放大到原来的2倍.
如图所示:
3.解:(1)把下面梯形的各边扩大到原来的3倍.
(2)把下面平行四边形的各边缩小到原来的.
如图所示:
4.解:(1)原来的面积:2.5×2÷2=2.5
新图形面积:5×4÷2=10
10÷2.5=4
答:新图形面积是原来面积的4倍.
(2)旋转后B点的位置是(1.5,4).
(3)平行四边形的面积是10,因为5×2=10,所以平行四边形的底是5,高是2.
(4)正方形的面积:5×4=20
4个三角形的面积:2.5×2÷2×2+3×1.5÷2×2
=5+4.5
=9.5
(20﹣9.5):20
=10.5:20
=21:40
答:涂色的正方形与大正方形的面积比是21:40.
画图如下:
故答案为:4,1.5,4,21:40.
5.解:图中三角形A的面积为:4×4÷2=8,
所画面积是8的平行四边形C的底为4,高为2;梯形D的上底为3,下底为5,高为2;
6.解:(1)、(2)作图如下:
(3)由图可知,图中圆的圆心位置用数对表示是(3,3).
将圆心先向右平移7格再向下平移2格的圆如上图:
最后将圆按3:1放大后画出来,放大后面积与原来面积的比是32:1=9:1.
故答案为;3,3,9:1
7.解:
(4+8)×4÷2
=12×4÷2
=24(平方厘米)
答:放大后的梯形的面积是24平方厘米.
七、解答题
1.解:(1)上面四个图形中,是轴对称图形的有
①和
③,(填序号)
(2)不是轴对称图形的图形上,再添上一个小正方形,使它成为轴对称图形,如图(答案不唯一).
(3)图中三角形先向南移动3格再向西移动2格后的图形,如图:
故答案为:①;③.
2.解:(1)按2:1画出如图中正方形放大后的图形(绿色),在放大后的正方形里画一个最大的圆(蓝色),并画出这个图形的对称轴(红色虚线).
(2)画出梯形绕点O按逆时针旋转90°后的图形(红色),此时点A用数对表示是(4,1).
故答案为:4,1.
3.解:根据题干分析可画图如下:
4.解:根据题干分析,可画图如下:
5.解:画图如下:
6.解:(1)张叔叔在笔直的公路上开车,方向盘的运动是
旋转现象.
(2)升国旗时,国旗的升降运动是
平移现象.
(3)妈妈用拖布擦地,是
平移现象.
(4)自行车的车轮转了一圈又一圈是
旋转现象.
故答案为:旋转;平移;平移;旋转.
一、填空题
1.下列现象,哪些是“平移”,哪些是“旋转”?分别填在括号里.
(1)张叔叔在笔直的公路上开车,方向盘的运动是
现象.
(2)升国旗时,国旗的升降运动是
现象.
(3)自行车的车轮转了一圈又一圈是
现象.
(4)妈妈用拖布擦地,是
现象.
2.边长4cm的正方形按2:1放大,得到的图形的面积是
cm2.
3.在横线上填“平移”或“旋转”.
(1)一辆汽车在一段笔直高速公路上行驶,这时车身的运动是
,车轮的运动是
.
(2)钟面上分钟的运动是
,秒钟的运动是
.
4.从4:15到4:30,分针将会按
时针方向旋转
°.
5.下面哪些图形是轴对称图形?请在括号中打“√”.
6.把长方形的每条边放大到原来的5倍,放大后的长方形与原来长方形对应边长的比是
;把底9厘米、高6厘米的三角形按1:3的比缩小后,三角形的底是
厘米,高是
厘米.
7.一张贺卡的长是6cm,宽是4cm,下面是三位小朋友画在方格纸上的贺卡示意图,谁画得像?在横线里画“√”.
笑笑
淘气
小斌
.
二、判断题
1.把圆的直径放大到原来的3倍,这个圆的面积就放大到原来的9倍.(
)
2.等腰三角形是轴对称图形.(
)
3.将图形缩小后得到的图形与原图形相比,大小不同,形状相同.(
)
4.把一个图形按1:2缩小,缩小后的周长是原图形周长的,缩小后的面积是原图形面积的.(
)
5.旋转运动中,物体的方向在变,位置不变.(
)
6.芳芳中午12点睡觉,下午闹钟2点准时响起,则时针在这段时间旋转了60°.(
)
7.在同一平面内两个完全相同的平面图形,其中一个通过平移、旋转的变换一定可以得到另一个.(
)
三、选择题
1.下列日常生活现象中,不属于平移的是( )
A.升国旗时,国旗的运动
B.在计数器上拨珠子的运动
C.荡起来的秋千
D.淘气在光滑的冰面上滑动
2.下面的哪组图形经过平移能够互相重合?( )
A.
B.
C.
3.有无数条对称轴的图形是( )
A.长方形
B.正方形
C.等边三角形
D.圆形
4.把一个正方形的各边按1:3缩小后,现在的图形和原来图形的面积比是( )
A.1:3
B.3:1
C.1:9
5.下面说法正确的是( )
A.旋转改变图形的形状和大小
B.平移改变图形的形状和大小
C.平移和旋转都不改变图形的形状和大小
6.下列图形中,对称轴最多的是( )
A.长方形
B.平行四边形
C.等边三角形
D.圆
7.一个三角形是轴对称图形,这个三角形一定是( )
A.锐角三角形
B.直角三角形
C.钝角三角形
D.等腰三角形
8.下列图形中对称轴最多的是( )
A.圆形
B.正方形
C.长方形
四.计算题
1.将图1的三角形按比例缩小后得到图2的三角形,求未知数x.
2.画出图形A按2:1放大后的图形C;画出图形B按1:2缩小后的图形D.
五、应用题
1.一个正方形放大后的边长是9厘米,放大后的面积是原来的9倍.这个正方形原来的边长是多少厘米?
2.小明在电脑上把一张长方形图片按比例放大后如图,放大后的宽是多少厘米?
六、操作题
1.画一画:把正方形各边放大到原来的2倍,把长方形各边缩小为原来的.
2.按要求在方格纸上画图.
(1)把正方形的边长缩小为原来的三分之一;
(2)把长方形的长和宽都放大到原来的2倍.
3.在方格纸上按要求画图.
(1)把下面梯形的各边扩大到原来的3倍.
(2)把下面平行四边形的各边缩小到原来的.
4.
(1)按照2:1的比画出三角形放大后的图形,新图形面积是原来面积的
倍.
(2)画出三角形绕A点逆时针方向旋转90°后的图形,旋转后B点的位置是(
,
).
(3)画一个平行四边形,面积与放大后的三角形面积相等.
(4)涂色的正方形与大正方形的面积比是
.
5.按1:2的比在图中画出三角形A缩小后的图形B,再画出和三角形A面积相等的平行四边形C和梯形D各一个.
6.操作题
(1)画出图①的另一半,使它成为一个轴对称图形.
(2)画出将图②绕A点顺时针旋转90°后的图形.
(3)图中圆的圆心位置用数对表示是(
,
).画出将圆先向右平移7格再向下平移2格后的图形.画出将圆按3:1的比放大后的图形,放大后面积与原来面积之比是
.
7.(1)把图中的长方形按1:2的比例缩小后的图形在网格线上画出来.
(2)把图中的梯形按2:1的比例放大后的图形在网格线上画出来.
(3)计算放大后的梯形的面积(1格长按1cm计算).
七、解答题
1.用4个相同的小正方形可以拼成下面几种图形.
(1)上面四个图形中,是轴对称图形的有
和
,(填序号)
(2)在不是轴对称图形的图形上,再添上一个小正方形,使它成为轴对称图形.
(3)画出上图中三角形先向南移动3格再向西移动2格后的图形,
2.按要求画一画.(每个小正方形的边长是1厘米)
(1)按2:1画出如图中正方形放大后的图形,在放大后的正方形里画一个最大的圆,并画出这个图形的对称轴.
(2)画出梯形绕点O按逆时针旋转90°后的图形,此时点A用数对表示是(
,
).
3.按要求在如图方格纸上画图.
①把图形绕点O顺时针旋转90度,得到图形B.
②把图形B向右平移4格得到图形C.
4.把图中的平行四边形先按2:1的比放大,画出放大后的图形,再绕A点顺时针旋转90°,画出旋转后的图形.
5.按要求在下面方格纸上画图.
(1)将下面的梯形按2:1放大.
(2)画出三角形ABC先向下平移4格,再向右平移3格后的图形.
(3)将三角形ABC绕C点顺时针方向旋转90°,画出旋转后的图形.
6.这些现象哪些是“平移”现象,哪些是“旋转”现象:
(1)张叔叔在笔直的公路上开车,方向盘的运动是
现象.
(2)升国旗时,国旗的升降运动是
现象.
(3)妈妈用拖布擦地,是
现象.
(4)自行车的车轮转了一圈又一圈是
现象.
答案
一、填空题
1.旋转,平移,旋转,平移.
2.64.
3.平移,旋转,旋转,旋转.
4.顺,90.
5.解:在平面图形中,长方形、正方形、圆、扇形、等腰三角形、等腰梯形都是轴对称图形.
6.5:1,3,2.
7.×,√,×.
二、判断题
1.√.2.√.3.√.4.√.5.×.6.√.7.×.
三、选择题
1.C.2.B.3.D.4.C.5.C.6.D.7.D.8.A.
四、计算题
1.解:设未知边为x,
1.6:x=3.2:4.8
3.2
x=1.6×4.8
x=2.4
答:未知数为2.4.
2.解:画出图形A按2:1放大后的图形C(下图红色部分);画出图形B按1:2缩小后的图形D(下图绿色部分):
五、应用题
1.解:因为这个正方形放大后面积是原来的9倍
所以这个正方形扩大了3倍
9÷3=3(厘米)
答:这个正方形原来的边长是3厘米.
2.解:18÷3=6
2×6=12(cm)
答:放大后的宽是12厘米.
六、操作题
1.解:把正方形各边放大到原来的2倍,把长方形各边缩小为原来的.
如图所示:
2.解:(1)把正方形的边长缩小为原来的三分之一;
(2)把长方形的长和宽都放大到原来的2倍.
如图所示:
3.解:(1)把下面梯形的各边扩大到原来的3倍.
(2)把下面平行四边形的各边缩小到原来的.
如图所示:
4.解:(1)原来的面积:2.5×2÷2=2.5
新图形面积:5×4÷2=10
10÷2.5=4
答:新图形面积是原来面积的4倍.
(2)旋转后B点的位置是(1.5,4).
(3)平行四边形的面积是10,因为5×2=10,所以平行四边形的底是5,高是2.
(4)正方形的面积:5×4=20
4个三角形的面积:2.5×2÷2×2+3×1.5÷2×2
=5+4.5
=9.5
(20﹣9.5):20
=10.5:20
=21:40
答:涂色的正方形与大正方形的面积比是21:40.
画图如下:
故答案为:4,1.5,4,21:40.
5.解:图中三角形A的面积为:4×4÷2=8,
所画面积是8的平行四边形C的底为4,高为2;梯形D的上底为3,下底为5,高为2;
6.解:(1)、(2)作图如下:
(3)由图可知,图中圆的圆心位置用数对表示是(3,3).
将圆心先向右平移7格再向下平移2格的圆如上图:
最后将圆按3:1放大后画出来,放大后面积与原来面积的比是32:1=9:1.
故答案为;3,3,9:1
7.解:
(4+8)×4÷2
=12×4÷2
=24(平方厘米)
答:放大后的梯形的面积是24平方厘米.
七、解答题
1.解:(1)上面四个图形中,是轴对称图形的有
①和
③,(填序号)
(2)不是轴对称图形的图形上,再添上一个小正方形,使它成为轴对称图形,如图(答案不唯一).
(3)图中三角形先向南移动3格再向西移动2格后的图形,如图:
故答案为:①;③.
2.解:(1)按2:1画出如图中正方形放大后的图形(绿色),在放大后的正方形里画一个最大的圆(蓝色),并画出这个图形的对称轴(红色虚线).
(2)画出梯形绕点O按逆时针旋转90°后的图形(红色),此时点A用数对表示是(4,1).
故答案为:4,1.
3.解:根据题干分析可画图如下:
4.解:根据题干分析,可画图如下:
5.解:画图如下:
6.解:(1)张叔叔在笔直的公路上开车,方向盘的运动是
旋转现象.
(2)升国旗时,国旗的升降运动是
平移现象.
(3)妈妈用拖布擦地,是
平移现象.
(4)自行车的车轮转了一圈又一圈是
旋转现象.
故答案为:旋转;平移;平移;旋转.
