七年级数学7.1.1 三角形的边
文档属性
| 名称 | 七年级数学7.1.1 三角形的边 |  | |
| 格式 | zip | ||
| 文件大小 | 869.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-03-15 17:12:01 | ||
图片预览







文档简介
(共32张PPT)
第七章 三角形
7.1.1 三角形的边
重庆市开县西街中学 罗堂喜
7.1 与三角形有关的线段
金字塔
分子结构
香港中银大厦
你能从中找到自己熟悉的图形吗?
★ 你所了解的三角形有些什么特点呢?
★ 你能根据自己的观察,给三角形下一个定义吗?
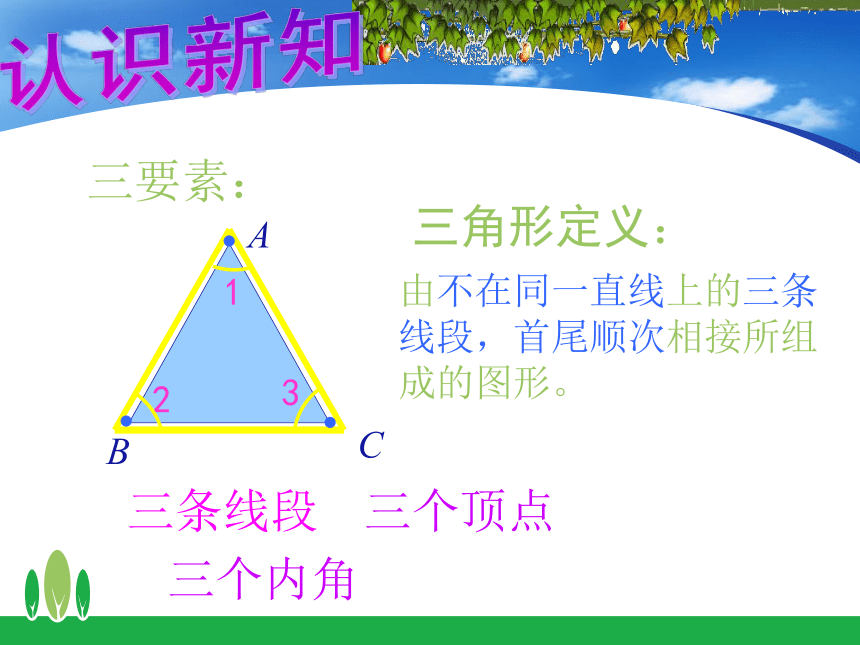
由不在同一直线上的三条线段,首尾顺次相接所组成的图形。
三个内角
B
A
C
三个顶点
三要素:
三条线段
三角形定义:
1
2
3
三角形的三要素
边:
如图三角形中三边 AB、BC、AC
顶点A所对的边BC也可表示为a,
顶点B所对的边AC也可表示为b ,
顶点C所对的边AB也可表示为c
角:
三角形中有三个角:
顶点:
三角形中有三个顶点:
∠A,∠B,∠C
顶点A,顶点B,顶点C
A
B
C
c
b
a
A
B
C
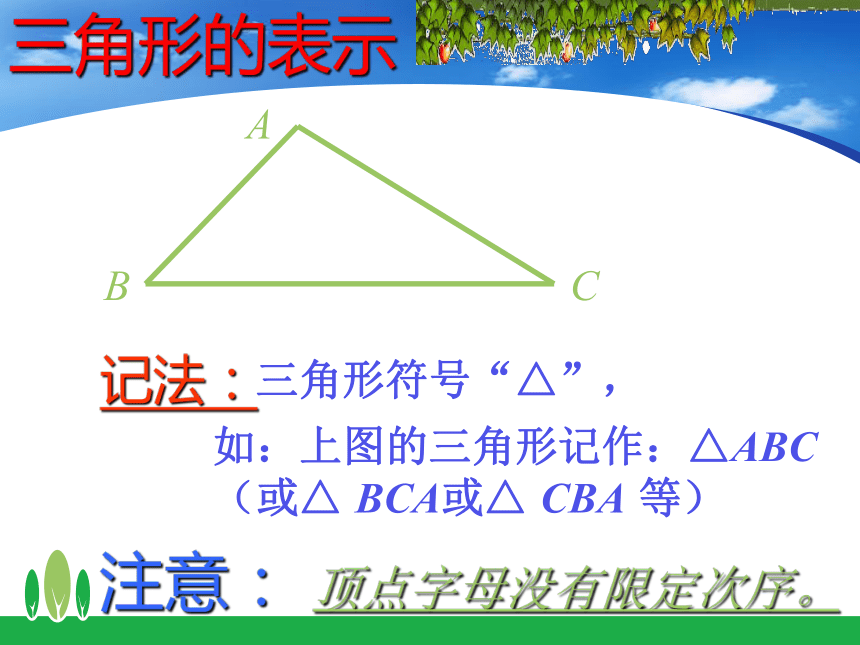
记法:
三角形符号“△”,
如:上图的三角形记作:△ABC (或△ BCA或△ CBA 等)
注意: 顶点字母没有限定次序。
三角形的表示
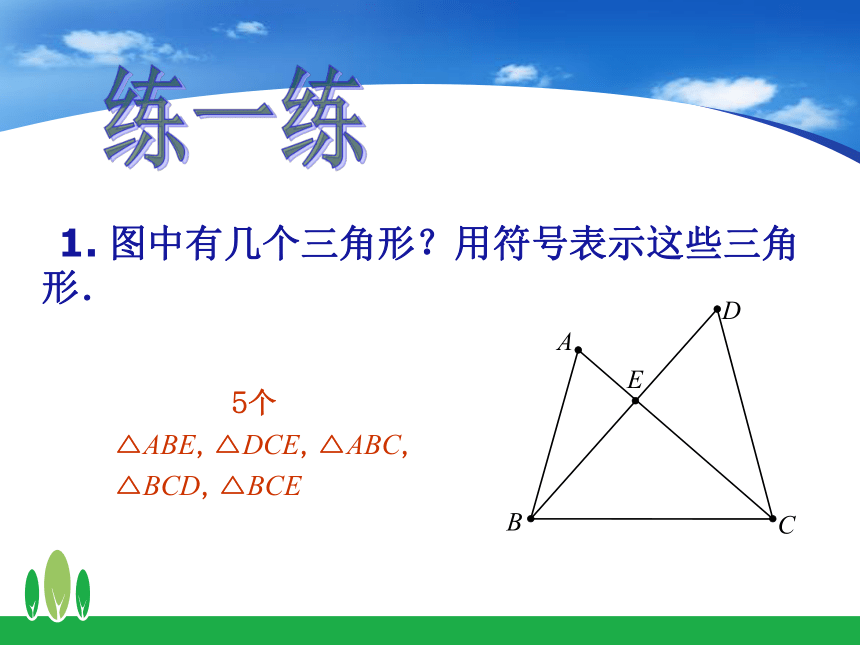
1. 图中有几个三角形?用符号表示这些三角形.
5个
△ABE, △DCE, △ABC,
△BCD, △BCE
E
D
C
B
A
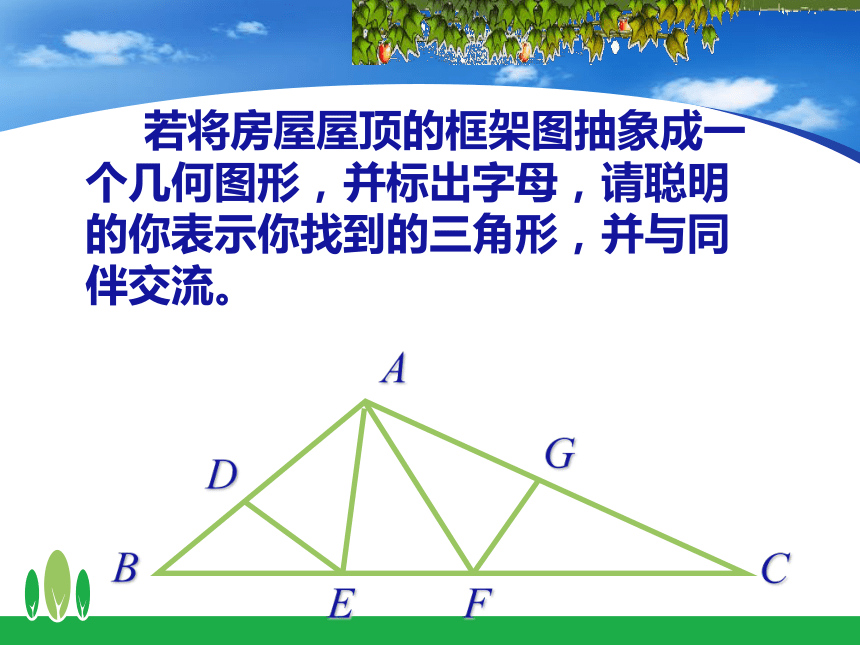
若将房屋屋顶的框架图抽象成一个几何图形,并标出字母,请聪明的你表示你找到的三角形,并与同伴交流。
A
B
C
D
E
F
G
2、如图,按要求完成下列填空.
(1)用符号表示图中的三角形 ;
(2)以BD为边的三角形有 ;
(3)以点A为一个顶点的三角形有 ;
(4)以∠C为一个内角的三角形有 .
△ABD,△BCD,△ABC
△ABD,△BCD
△ABD,△ABC
△BCD,△ABC
D
C
B
A
图上的三角形分别有怎样的特点呢?它属于哪一种三角形呢?
【按三个内角大小分】
三角形
锐角三角形
直角三角形
钝角三角形
【按边的相等关系分】
三角形
不等边三角形
等腰三角形
底边和腰不相等
的等腰三角形
等边三角形
两点之间的所有连线中,线段最短
在A点的小狗,为了尽快吃到B点的香肠,它选择A B路线,而不选择A C B路线,难道小狗也懂数学?
C
B
A
谈谈你的想法!
即:
三角形两边的和大于第三边
C
B
A
问题:在一个三角形中,任意两边之差和第三边有着怎样的关系?说明你的理由.
三角形任意两边之差小于第三边;
下列长度的三条线段能否组成三角形?
为什么?
(1)3,4,8;
(2)5,6,11;
(3)5,6,10.
不能
不能
能
只要比较两较短线段之和与最长线的大小即可。
解题技巧:
人行横道
你能用数学知识解释吗
为什么经常有些行人斜穿马路而不走人行横道
或两点之间的所有连线中,线段最短
三角形任意两边之和大于第三边。
A
B
理由:
C
.
小晶有两根长度为5cm、8cm的木条,她想钉一个三角形的木框,现在有长度分别为2cm 、3cm、 8cm 、15cm的木条供她选择,那她第三根应选择?( ) A、2cm B、3cm C、8cm D、15cm
分析: ∵ 第三根可选择的范围是:
大于8-5=3(cm)小于8+5=13(cm)
∴只有8cm的木条能钉成三角形木框,所以答案选C.
解题技巧:
三角形第三边的取值范围是:
两边之差<第三边<两边之和
问题
有四根长度分别是2cm,3cm,
4cm, 5cm的木棒,选取其中的三根
围成一个三角形,有几种方法?谈谈
你的看法 .
有三种方法围成三角形:
(1)2cm,3cm,4cm;
(2)3cm,4cm,5cm;
(3)2cm,4cm,5cm.
【例】用一条长为18cm的细绳围成
一个等腰三角形.
(1)如果腰长是底边的2倍,那么
各边的长是多少?
(2)能围成有一边的长为4cm的等
腰三角形吗?为什么?
…
1.你会数三角形吗?下列各图中各有几个三角形?
( 3 )
( 6 )
( … )
( ? )
数完后请说出你发现的规律。
2.在 ABC中,AB=7 BC=3,并且AC为奇数,那么 ABC的周长是多少?
有A、B、C、D四个村庄,打算公用一个水厂,若要使所用的水管最节约,水厂应过村庄的什么地方?
●
O
●
●
●
●
A
B
C
D
●
P
问题
如图,点P是△ABC内部一点,连接
BP延长后交AC于点D.
1.试探究线段AB+BC+CA与线段2BD
的大小关系;
2.试探究AB+AC与PB+PC
的大小关系.
〔解答〕
(1)在△ ABD中,AB+AD>BD.
在△ BCD中,BC+CD>BD.
两式相加可以得到
AB+AD+CD+BC>2BD .
(2)在△ ABD中,AB+AD>BP+PD,
在△ PDC中有PD+DC>PC,
上述两式相加得到
AB+AD+PD+CD>BP+PD+PC,
即,AB+AC>BP+PC.
一个三角形有两边相等,周长是24,
且一边是4,求其他两边长.
问题
(1)当4是相等的两边长时,另一边长是24-8=16,即三边是4、4、16,根据三角形三边关系不能构成三角形;
(2)当4不是相等两边长时,另两边长是(24-4)÷2=10,即4、10、10符合三角形的三边关系,于是这个三角形的另两边长是10、10.
已知一个三角形的两边长分别为2cm和13cm,
若该三角形的周长为奇数,则第三边长为多少?
答案:12cm或14cm
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
小结与作业
小结:本节课我们学习了三角形的概念及基本要素,重点研究了三角形的三边关系.
(1)从三角形三边关系的研究中可知,三角形的三边相互制约——任意两边之和大于第三边,且任意两边之差小于第三边.
(2)判断a、b、c三条线段能否组成一个三角形,应注意:a+b>c,b+c>a,a+c>b.三个条件缺一不可.当a是a、b、c三条线段中最长的一条时,只要b+c>a,就有任意两条线段的和大于第三边.
必做题:书第69页第1、2、6题,
第70页第7题.
选做题:如图,线段AB,CD相交于点O,
能否确定AB+CD与AD+BC的大小关系,请
说明理由.
第七章 三角形
7.1.1 三角形的边
重庆市开县西街中学 罗堂喜
7.1 与三角形有关的线段
金字塔
分子结构
香港中银大厦
你能从中找到自己熟悉的图形吗?
★ 你所了解的三角形有些什么特点呢?
★ 你能根据自己的观察,给三角形下一个定义吗?
由不在同一直线上的三条线段,首尾顺次相接所组成的图形。
三个内角
B
A
C
三个顶点
三要素:
三条线段
三角形定义:
1
2
3
三角形的三要素
边:
如图三角形中三边 AB、BC、AC
顶点A所对的边BC也可表示为a,
顶点B所对的边AC也可表示为b ,
顶点C所对的边AB也可表示为c
角:
三角形中有三个角:
顶点:
三角形中有三个顶点:
∠A,∠B,∠C
顶点A,顶点B,顶点C
A
B
C
c
b
a
A
B
C
记法:
三角形符号“△”,
如:上图的三角形记作:△ABC (或△ BCA或△ CBA 等)
注意: 顶点字母没有限定次序。
三角形的表示
1. 图中有几个三角形?用符号表示这些三角形.
5个
△ABE, △DCE, △ABC,
△BCD, △BCE
E
D
C
B
A
若将房屋屋顶的框架图抽象成一个几何图形,并标出字母,请聪明的你表示你找到的三角形,并与同伴交流。
A
B
C
D
E
F
G
2、如图,按要求完成下列填空.
(1)用符号表示图中的三角形 ;
(2)以BD为边的三角形有 ;
(3)以点A为一个顶点的三角形有 ;
(4)以∠C为一个内角的三角形有 .
△ABD,△BCD,△ABC
△ABD,△BCD
△ABD,△ABC
△BCD,△ABC
D
C
B
A
图上的三角形分别有怎样的特点呢?它属于哪一种三角形呢?
【按三个内角大小分】
三角形
锐角三角形
直角三角形
钝角三角形
【按边的相等关系分】
三角形
不等边三角形
等腰三角形
底边和腰不相等
的等腰三角形
等边三角形
两点之间的所有连线中,线段最短
在A点的小狗,为了尽快吃到B点的香肠,它选择A B路线,而不选择A C B路线,难道小狗也懂数学?
C
B
A
谈谈你的想法!
即:
三角形两边的和大于第三边
C
B
A
问题:在一个三角形中,任意两边之差和第三边有着怎样的关系?说明你的理由.
三角形任意两边之差小于第三边;
下列长度的三条线段能否组成三角形?
为什么?
(1)3,4,8;
(2)5,6,11;
(3)5,6,10.
不能
不能
能
只要比较两较短线段之和与最长线的大小即可。
解题技巧:
人行横道
你能用数学知识解释吗
为什么经常有些行人斜穿马路而不走人行横道
或两点之间的所有连线中,线段最短
三角形任意两边之和大于第三边。
A
B
理由:
C
.
小晶有两根长度为5cm、8cm的木条,她想钉一个三角形的木框,现在有长度分别为2cm 、3cm、 8cm 、15cm的木条供她选择,那她第三根应选择?( ) A、2cm B、3cm C、8cm D、15cm
分析: ∵ 第三根可选择的范围是:
大于8-5=3(cm)小于8+5=13(cm)
∴只有8cm的木条能钉成三角形木框,所以答案选C.
解题技巧:
三角形第三边的取值范围是:
两边之差<第三边<两边之和
问题
有四根长度分别是2cm,3cm,
4cm, 5cm的木棒,选取其中的三根
围成一个三角形,有几种方法?谈谈
你的看法 .
有三种方法围成三角形:
(1)2cm,3cm,4cm;
(2)3cm,4cm,5cm;
(3)2cm,4cm,5cm.
【例】用一条长为18cm的细绳围成
一个等腰三角形.
(1)如果腰长是底边的2倍,那么
各边的长是多少?
(2)能围成有一边的长为4cm的等
腰三角形吗?为什么?
…
1.你会数三角形吗?下列各图中各有几个三角形?
( 3 )
( 6 )
( … )
( ? )
数完后请说出你发现的规律。
2.在 ABC中,AB=7 BC=3,并且AC为奇数,那么 ABC的周长是多少?
有A、B、C、D四个村庄,打算公用一个水厂,若要使所用的水管最节约,水厂应过村庄的什么地方?
●
O
●
●
●
●
A
B
C
D
●
P
问题
如图,点P是△ABC内部一点,连接
BP延长后交AC于点D.
1.试探究线段AB+BC+CA与线段2BD
的大小关系;
2.试探究AB+AC与PB+PC
的大小关系.
〔解答〕
(1)在△ ABD中,AB+AD>BD.
在△ BCD中,BC+CD>BD.
两式相加可以得到
AB+AD+CD+BC>2BD .
(2)在△ ABD中,AB+AD>BP+PD,
在△ PDC中有PD+DC>PC,
上述两式相加得到
AB+AD+PD+CD>BP+PD+PC,
即,AB+AC>BP+PC.
一个三角形有两边相等,周长是24,
且一边是4,求其他两边长.
问题
(1)当4是相等的两边长时,另一边长是24-8=16,即三边是4、4、16,根据三角形三边关系不能构成三角形;
(2)当4不是相等两边长时,另两边长是(24-4)÷2=10,即4、10、10符合三角形的三边关系,于是这个三角形的另两边长是10、10.
已知一个三角形的两边长分别为2cm和13cm,
若该三角形的周长为奇数,则第三边长为多少?
答案:12cm或14cm
对自己说,你有什么收获?
对同学说,你有什么温馨提示?
小结与作业
小结:本节课我们学习了三角形的概念及基本要素,重点研究了三角形的三边关系.
(1)从三角形三边关系的研究中可知,三角形的三边相互制约——任意两边之和大于第三边,且任意两边之差小于第三边.
(2)判断a、b、c三条线段能否组成一个三角形,应注意:a+b>c,b+c>a,a+c>b.三个条件缺一不可.当a是a、b、c三条线段中最长的一条时,只要b+c>a,就有任意两条线段的和大于第三边.
必做题:书第69页第1、2、6题,
第70页第7题.
选做题:如图,线段AB,CD相交于点O,
能否确定AB+CD与AD+BC的大小关系,请
说明理由.
