点与圆的位置关系课件
图片预览







文档简介
(共21张PPT)
中国射击运动员--------杜丽
24.2与圆有关的位置关系
点和圆的位置关系
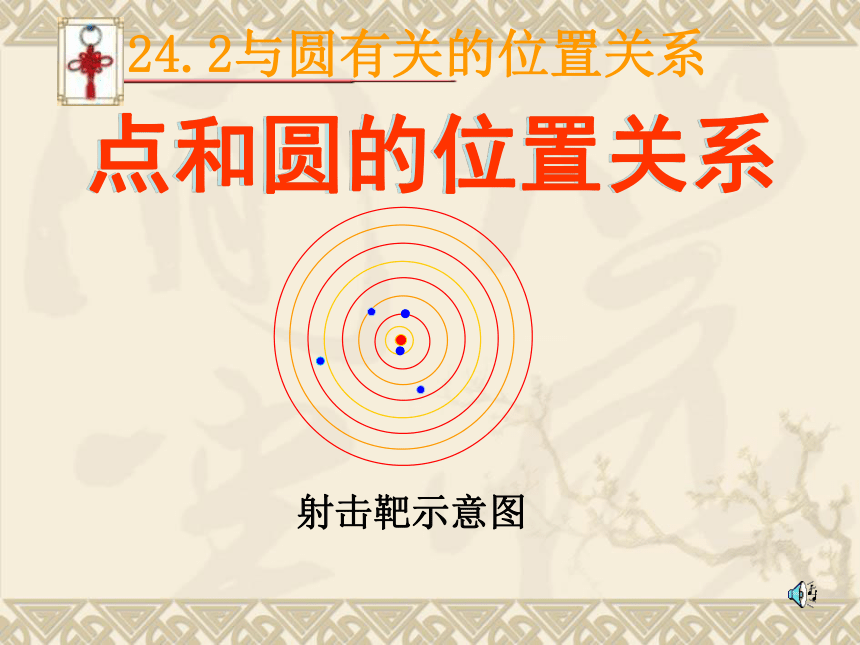
射击靶示意图
1、请你在练习本上画一个圆,然后任意作一些点,观察这些点和圆的位置关系。
2、量一量这些点到圆心的距离。你发现了什么?
探究活动:
点在圆内 、点在圆上、点在圆外
设⊙O的半径为r,点到圆心的距离为d。则
点和圆的位置关系
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d>r
练习一:已知圆的半径等于5厘米,点到圆心的距离是:
(1)8厘米 (2)4厘米 (3)5厘米。
请你分别说出点与圆的位置关系。
●
●
●
练习二:
1、已知⊙O的半径为4,OP=3.4,则P在⊙O的 ( )。
2、已知 点P在 ⊙O的外部,OP=5,那么⊙O的半径r满足( )
3、 已知⊙O的半径为5,M为ON的中点,当OM=3时,N点与⊙O的位置关系是N在⊙O的( )
4、 ⊙O直径为d,点A到圆心的距离为m,若点
A不在圆外,则d与m的关系是( )
内部
0﹤r ﹤5
外部
d/2≥m
中国射击运动员--------杜丽
一位考古学家在马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
挑战自我:
过几点可以确定一个圆呢?
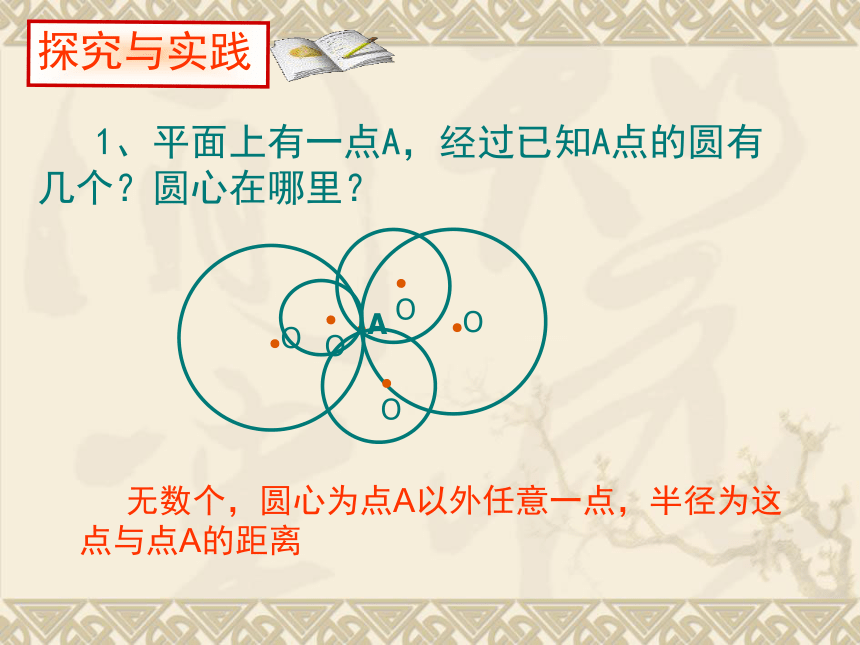
1、平面上有一点A,经过已知A点的圆有几个?圆心在哪里?
●O
●A
●O
●O
●O
●O
无数个,圆心为点A以外任意一点,半径为这点与点A的距离
探究与实践
2、平面上有两点A、B,经过已知点A、B的圆有几个?它们的圆心分布有什么特点?
探究与实践
●O
● O
●O
●O
A
B
以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆.
无数个。它们的圆心都在线段AB的垂直平分线上。
3、过同一平面内三个点能作圆吗?
1)、当三点A、B、C不在同一直线上。
2)当三点A、B、C在同一直线上时,可以作几个圆?
不能作出。
A
B
C
O
探究与实践
A
B
C
过如下三点为什么不能做圆
不在同一直线上的三点确定一个圆
结论:
4、你能过三角形的三个顶点作圆吗?如何作?
A
B
C
O
探究与实践
B
A
C
O
●
想一想:
你能过锐角三角形、直角三角形、钝角三角形的的三个顶点作圆吗?它们的圆心分别在哪里?
B
●
C
A
B
A
C
·
过任意三角形的三个顶点都可以作圆
三角形与圆
因此,三角形的三个顶点确定一个圆,这圆叫做三角形的外接圆.这个三角形叫做圆的内接三角形.
外接圆的圆心是三角形三边垂直平分线的的交点,叫做三角形的外心.
●O
A
B
C
?思考:三角形的外心都在三角形的内部吗
B
A
C
O
●
1.锐角三角形的外心在三角形的内部。
2.直角三角形的外心在三角形的斜边上,
且是斜边的中点
3.钝角三角形的外心在三角形的外部
B
●
C
A
B
A
C
·
B
A
C
O
完成填空:
如图:⊙O是△ ABC的 圆, △ ABC 是⊙O的 三角形,O是△ ABC的 心,它是 的交点,到三角形 的三个顶点的距离相等。
●
外接
内接
外
三边垂直平分线
思考:一个三角形的外接圆有几个
一个圆的内接三角形有几个
一个
无数个
如何解决“破镜重圆”的问题:
解决问题的关键是什么?
(找圆心)
A
B
C
O
课堂检测:
判断:
1、经过三点一定可以作圆。( )
2、三角形的外心就是这个三角形两边垂直平分线的交点。( )
3、三角形的外心到三边的距离相等。( )
4、经过不在一直线上的四点能作一个圆。( )
填空:
1、在△ABC中,∠C=90°, ∠A=30°,BC=3㎝,则
△ABC外接圆的半径是___
2、在△ABC中,AB=5,AC=12,BC=13,三角形的外心在
___上,半径长为___
×
√
×
×
3㎝
BC中点
6.5
这节课你学到了哪些知识?有什么感想
回顾与思考
课后思考题:
探究四点共圆的条件是什么
今天作业:
课本P93页1、2、3题
中国射击运动员--------杜丽
24.2与圆有关的位置关系
点和圆的位置关系
射击靶示意图
1、请你在练习本上画一个圆,然后任意作一些点,观察这些点和圆的位置关系。
2、量一量这些点到圆心的距离。你发现了什么?
探究活动:
点在圆内 、点在圆上、点在圆外
设⊙O的半径为r,点到圆心的距离为d。则
点和圆的位置关系
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d>r
练习一:已知圆的半径等于5厘米,点到圆心的距离是:
(1)8厘米 (2)4厘米 (3)5厘米。
请你分别说出点与圆的位置关系。
●
●
●
练习二:
1、已知⊙O的半径为4,OP=3.4,则P在⊙O的 ( )。
2、已知 点P在 ⊙O的外部,OP=5,那么⊙O的半径r满足( )
3、 已知⊙O的半径为5,M为ON的中点,当OM=3时,N点与⊙O的位置关系是N在⊙O的( )
4、 ⊙O直径为d,点A到圆心的距离为m,若点
A不在圆外,则d与m的关系是( )
内部
0﹤r ﹤5
外部
d/2≥m
中国射击运动员--------杜丽
一位考古学家在马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
挑战自我:
过几点可以确定一个圆呢?
1、平面上有一点A,经过已知A点的圆有几个?圆心在哪里?
●O
●A
●O
●O
●O
●O
无数个,圆心为点A以外任意一点,半径为这点与点A的距离
探究与实践
2、平面上有两点A、B,经过已知点A、B的圆有几个?它们的圆心分布有什么特点?
探究与实践
●O
● O
●O
●O
A
B
以线段AB的垂直平分线上的任意一点为圆心,以这点到A或B的距离为半径作圆.
无数个。它们的圆心都在线段AB的垂直平分线上。
3、过同一平面内三个点能作圆吗?
1)、当三点A、B、C不在同一直线上。
2)当三点A、B、C在同一直线上时,可以作几个圆?
不能作出。
A
B
C
O
探究与实践
A
B
C
过如下三点为什么不能做圆
不在同一直线上的三点确定一个圆
结论:
4、你能过三角形的三个顶点作圆吗?如何作?
A
B
C
O
探究与实践
B
A
C
O
●
想一想:
你能过锐角三角形、直角三角形、钝角三角形的的三个顶点作圆吗?它们的圆心分别在哪里?
B
●
C
A
B
A
C
·
过任意三角形的三个顶点都可以作圆
三角形与圆
因此,三角形的三个顶点确定一个圆,这圆叫做三角形的外接圆.这个三角形叫做圆的内接三角形.
外接圆的圆心是三角形三边垂直平分线的的交点,叫做三角形的外心.
●O
A
B
C
?思考:三角形的外心都在三角形的内部吗
B
A
C
O
●
1.锐角三角形的外心在三角形的内部。
2.直角三角形的外心在三角形的斜边上,
且是斜边的中点
3.钝角三角形的外心在三角形的外部
B
●
C
A
B
A
C
·
B
A
C
O
完成填空:
如图:⊙O是△ ABC的 圆, △ ABC 是⊙O的 三角形,O是△ ABC的 心,它是 的交点,到三角形 的三个顶点的距离相等。
●
外接
内接
外
三边垂直平分线
思考:一个三角形的外接圆有几个
一个圆的内接三角形有几个
一个
无数个
如何解决“破镜重圆”的问题:
解决问题的关键是什么?
(找圆心)
A
B
C
O
课堂检测:
判断:
1、经过三点一定可以作圆。( )
2、三角形的外心就是这个三角形两边垂直平分线的交点。( )
3、三角形的外心到三边的距离相等。( )
4、经过不在一直线上的四点能作一个圆。( )
填空:
1、在△ABC中,∠C=90°, ∠A=30°,BC=3㎝,则
△ABC外接圆的半径是___
2、在△ABC中,AB=5,AC=12,BC=13,三角形的外心在
___上,半径长为___
×
√
×
×
3㎝
BC中点
6.5
这节课你学到了哪些知识?有什么感想
回顾与思考
课后思考题:
探究四点共圆的条件是什么
今天作业:
课本P93页1、2、3题
