2020-2021学年高一下学期数学人教A版(2019)必修第二册 8.6.3 平面与平面垂直(第一课时)课件(共32张PPT)
文档属性
| 名称 | 2020-2021学年高一下学期数学人教A版(2019)必修第二册 8.6.3 平面与平面垂直(第一课时)课件(共32张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 17.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 00:00:00 | ||
图片预览





文档简介
8.6.3 平面与平面垂直(第一课时)
高一年级 数学
主讲人
日期:2021.05.08
编号:202105062141
学 习 目 标
1、从相关定义和基本事实出发,借助长方体,通过直观感知,
了解空间平面与平面的垂直关系.
2、了解二面角的相关概念,平面与平面垂直的定义.
3、归纳出平面与平面垂直的判定定理.
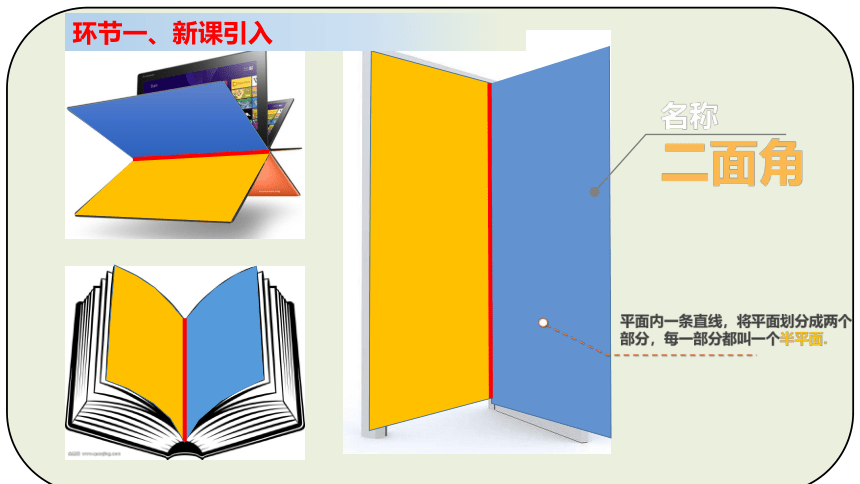
环节一、新课引入
环节一、新课引入
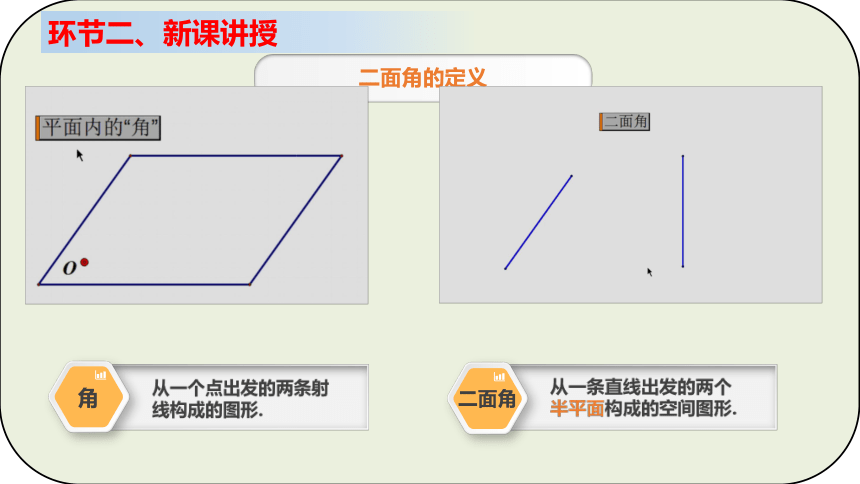
二面角的定义
二面角
角
环节二、新课讲授
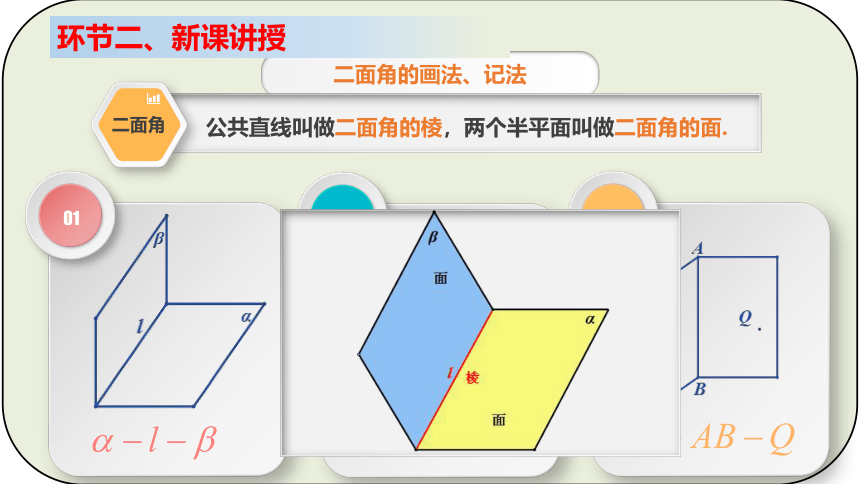
二面角的画法、记法
二面角
公共直线叫做二面角的棱,两个半平面叫做二面角的面.
01
02
03
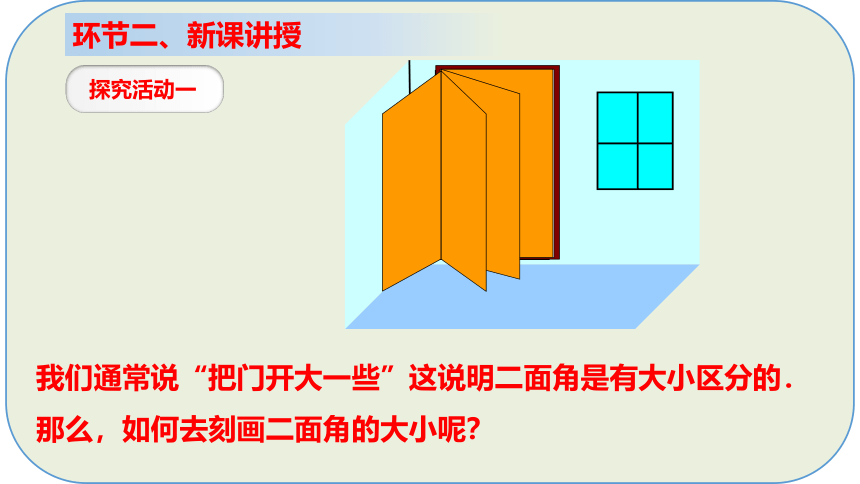
环节二、新课讲授
我们通常说“把门开大一些”这说明二面角是有大小区分的.那么,如何去刻画二面角的大小呢?
环节二、新课讲授
探究活动一
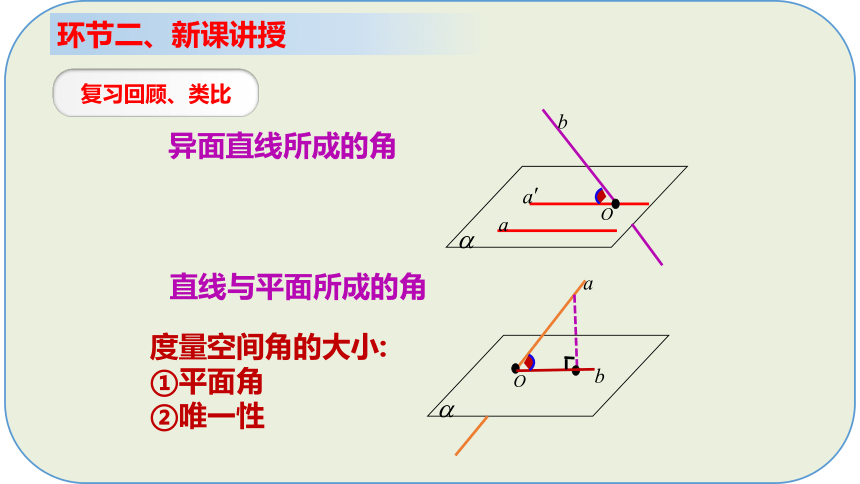
异面直线所成的角
直线与平面所成的角
度量空间角的大小:
①平面角
②唯一性
环节二、新课讲授
复习回顾、类比
小组活动:用空白纸折出一个二面角,以小组为单位,讨论后画出一个平面角来表示二面角的大小.
小组合作
环节二、新课讲授
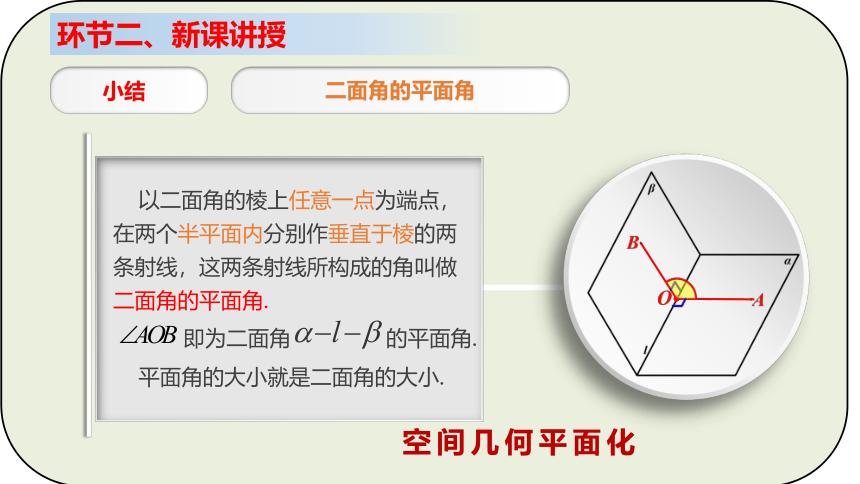
二面角的平面角
以二面角的棱上任意一点为端点,在两个半平面内分别作垂直于棱的两条射线,这两条射线所构成的角叫做二面角的平面角.
即为二面角 的平面角.
平面角的大小就是二面角的大小.
空间几何平面化
环节二、新课讲授
小结
二面角的平面角
①顶点在棱上;
②两边分别在两个面内;
③两边都要垂直于二面角的棱.
二面角的平面角必须满足
二面角的平面角大小与顶点在棱上的位置无关,只与二面角的张角大小有关.
平面角大小的唯一性
二面角的范围
当两个半平面重合时,规定
当两个半平面合成平面时,规定
环节二、新课讲授
小结
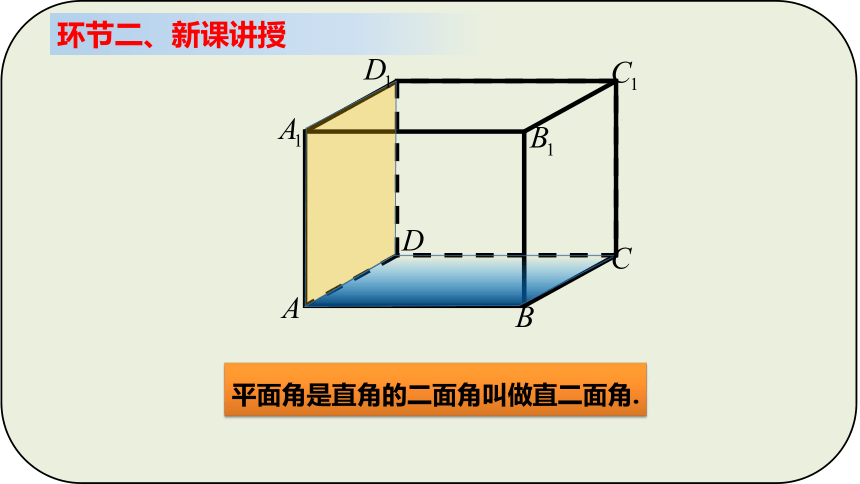
平面角是直角的二面角叫做直二面角.
环节二、新课讲授
面面垂直的定义
平面角是直角的二面角叫做直二面角;
此时,称两平面互相垂直,记为 .
定义是判定面面
垂直的方法之一.
环节二、新课讲授
找到一个面面垂直的实例,指出实例中哪两个平面互相垂直,说明使得该组平面垂直的原因,并尝试总结判定两平面垂直的一般方法,小组开展讨论.
拆
探究活动二
环节二、新课讲授
结论:一个平面内一条线垂直于另一平面,则这两个平面垂直。
真假?
探究活动二
环节二、新课讲授
环节二、新课讲授
平面与平面垂直的判定定理
一个平面经过另一个平面的一条垂线,则这两个平面互相垂直.
图形表示
符号表示
面面垂直
线面垂直
线线垂直
环节二、新课讲授
×
×
√
√
思考:判断
环节二、新课讲授
环节三、例题讲解
例题 如图所示,在正方体ABCD-A'B'C'D'中,
求证:平面A'BD⊥平面ACC'A'.
分析:要证平面A'BD ⊥ 平面ACC'A',
只需要证明平面A'BD经过平面ACC'A'的一条垂线(两个平面垂直的判定定理).
需要证明平面A'BD内的一条直线垂直于平面ACC'A'内的两条相交直线(直线与平面垂直的判定定理).
这些由正方体的性质很容易得到.
环节三、例题讲解
例题 如图所示,在正方体ABCD-A'B'C'D'中,
求证:平面A'BD⊥平面ACC'A'.
证明:∵ ABCD-A'B'C'D' 是正方体,
∴AA'⊥平面ABCD.
又∵BD ?平面ABCD,
?
又∵BD⊥AC,AC∩AA' =A,
∴BD⊥平面ACC'A' .
∴平面A'BD ⊥ 平面ACC'A'.
∴AA' ⊥BD.
又∵BD ?平面A' BD,
?
练一练
biē nào
环节三、例题讲解
面面垂直
线面垂直
线线垂直
环节三、例题讲解
例题 AB 是☉O的直径,PA垂直于☉O所在的平面,C 是
圆周上不同于A,B的任意一点.
求证:平面PAC⊥平面PBC.
分析:要证明两个平面垂直
只需要证明其中一个平面内的一条直线垂直于另一个平面即可(两个平面垂直的判定定理)
需要证明这条直线与另一个平面内的两条相交直线垂直(直线和平面垂直的判定定理知).
本题中,利用直线与平面垂直的性质以及圆的性质易得所需条件.
环节三、例题讲解
∴PA⊥BC.
证明:∵PA⊥平面ABC,BC ?平面ABC,
?
∵点C是圆周上不同于A,B的任意一点,
且AB是☉O的直径,
∴∠ACB=90°,即BC⊥AC.
又∵ PA ∩ AC=A,PA、AC ?平面PAC,
?
∴BC⊥平面PAC.
∴平面PAC ⊥平面PBC.
又∵BC ?平面PBC,
?
环节四、习题练习
5min完成练习1~4
1. 如图,检查工件的相邻两个(平)面是否垂直时,只要用曲尺的一边
紧靠在工件的一个面上,另一边在工件的另一个面上转动,观察尺边和
这个面是否密合就可以了.这是为什么?
答:由面面垂直的判定定理可知:转动时,如果尺边
与这个面密合,则说明另一尺边垂直于这个面,于是
工件的相邻两个面互相垂直.
环节四、习题练习
2.已知直线????,????与平面????,????,????,能使????⊥????的充分条件是( )
A. ????⊥????,????⊥???? B. ????∩??=????,????⊥????,?????????
C. ????//????,????//???? D. ????//????,????⊥????
?
分析:A. 不正确,反例如图所示.
B. 由 ????∩????=????,????⊥????,不能推出????⊥????,所以也不能推出????⊥????.
?
C. 由 ????//????,????//????可得,????//????,或????∩????=????且????//????,但????⊥????不一定成立.
?
环节四、习题练习
2.已知直线????,????与平面????,????,????,能使????⊥????的充分条件是( )
A. ????⊥????,????⊥???? B. ????∩????=????,????⊥????,?????????
C. ????//????,????//???? D. ????//????,????⊥????
?
分析:
D. ∵????//????,∴可以过直线????做一平面????∩????=????,则????//????.
?
∵????⊥????,∴????⊥????.
?
∵直线?????????,∴????⊥????.
?
D
环节四、习题练习
3.如图,????????⊥平面????????????,????????⊥????????,你能发现哪些平面互相垂直,为什么?
?
∵????????⊥平面????????????,?????????平面????????????,∴平面????????????⊥平面????????????.
?
同理,平面????????????⊥平面????????????.
?
∵????????⊥平面????????????,?????????平面????????????
∴????????⊥????????.
?
∵????????⊥????????,∴????????⊥平面????????????.
?
∵?????????平面??????????,∴平面????????????⊥平面????????????.
?
答:平面????????????⊥平面????????????,平面????????????⊥平面????????????,平面????????????⊥平面????????????.
?
环节四、习题练习
4.如图,在正三棱柱?????????????????′????′????′中,????为棱????????的中点.
求证:平面????????????′⊥平面????????????′????′.
?
证明:∵?????????????????′????′????′是正三棱柱,∴????????′⊥平面????????????.
?
(正三棱柱的定义)
∵?????????平面????????????,∴????????′⊥????????.
?
(线面垂直的定义)
∵△????????????是正三角形,????为????????的中点,∴????????⊥????????.
?
(平面几何知识)
∵????????∩????????′=????,∴????????⊥平面????????????′????′.
?
(线面垂直的判定)
∵?????????平面????????????′,∴平面????????????′⊥平面????????????′????′.
?
(面面垂直的判定)
方法收获
知识收获
环节五、归纳总结
2.(选做题)研究性作业
1.(必做题)
完成课本第163页,习题8.6的第7、8题
观察生活中的面面垂直关系,结合本节课的探究经验,你还能有其它进一步的认识吗?
请试着将空间中的线面垂直关系形成体系,绘制一个思维导图.
下节,精彩继续……
重庆市南开中学 赵爽
谢 谢
高一年级 数学
主讲人
日期:2021.05.08
编号:202105062141
学 习 目 标
1、从相关定义和基本事实出发,借助长方体,通过直观感知,
了解空间平面与平面的垂直关系.
2、了解二面角的相关概念,平面与平面垂直的定义.
3、归纳出平面与平面垂直的判定定理.
环节一、新课引入
环节一、新课引入
二面角的定义
二面角
角
环节二、新课讲授
二面角的画法、记法
二面角
公共直线叫做二面角的棱,两个半平面叫做二面角的面.
01
02
03
环节二、新课讲授
我们通常说“把门开大一些”这说明二面角是有大小区分的.那么,如何去刻画二面角的大小呢?
环节二、新课讲授
探究活动一
异面直线所成的角
直线与平面所成的角
度量空间角的大小:
①平面角
②唯一性
环节二、新课讲授
复习回顾、类比
小组活动:用空白纸折出一个二面角,以小组为单位,讨论后画出一个平面角来表示二面角的大小.
小组合作
环节二、新课讲授
二面角的平面角
以二面角的棱上任意一点为端点,在两个半平面内分别作垂直于棱的两条射线,这两条射线所构成的角叫做二面角的平面角.
即为二面角 的平面角.
平面角的大小就是二面角的大小.
空间几何平面化
环节二、新课讲授
小结
二面角的平面角
①顶点在棱上;
②两边分别在两个面内;
③两边都要垂直于二面角的棱.
二面角的平面角必须满足
二面角的平面角大小与顶点在棱上的位置无关,只与二面角的张角大小有关.
平面角大小的唯一性
二面角的范围
当两个半平面重合时,规定
当两个半平面合成平面时,规定
环节二、新课讲授
小结
平面角是直角的二面角叫做直二面角.
环节二、新课讲授
面面垂直的定义
平面角是直角的二面角叫做直二面角;
此时,称两平面互相垂直,记为 .
定义是判定面面
垂直的方法之一.
环节二、新课讲授
找到一个面面垂直的实例,指出实例中哪两个平面互相垂直,说明使得该组平面垂直的原因,并尝试总结判定两平面垂直的一般方法,小组开展讨论.
拆
探究活动二
环节二、新课讲授
结论:一个平面内一条线垂直于另一平面,则这两个平面垂直。
真假?
探究活动二
环节二、新课讲授
环节二、新课讲授
平面与平面垂直的判定定理
一个平面经过另一个平面的一条垂线,则这两个平面互相垂直.
图形表示
符号表示
面面垂直
线面垂直
线线垂直
环节二、新课讲授
×
×
√
√
思考:判断
环节二、新课讲授
环节三、例题讲解
例题 如图所示,在正方体ABCD-A'B'C'D'中,
求证:平面A'BD⊥平面ACC'A'.
分析:要证平面A'BD ⊥ 平面ACC'A',
只需要证明平面A'BD经过平面ACC'A'的一条垂线(两个平面垂直的判定定理).
需要证明平面A'BD内的一条直线垂直于平面ACC'A'内的两条相交直线(直线与平面垂直的判定定理).
这些由正方体的性质很容易得到.
环节三、例题讲解
例题 如图所示,在正方体ABCD-A'B'C'D'中,
求证:平面A'BD⊥平面ACC'A'.
证明:∵ ABCD-A'B'C'D' 是正方体,
∴AA'⊥平面ABCD.
又∵BD ?平面ABCD,
?
又∵BD⊥AC,AC∩AA' =A,
∴BD⊥平面ACC'A' .
∴平面A'BD ⊥ 平面ACC'A'.
∴AA' ⊥BD.
又∵BD ?平面A' BD,
?
练一练
biē nào
环节三、例题讲解
面面垂直
线面垂直
线线垂直
环节三、例题讲解
例题 AB 是☉O的直径,PA垂直于☉O所在的平面,C 是
圆周上不同于A,B的任意一点.
求证:平面PAC⊥平面PBC.
分析:要证明两个平面垂直
只需要证明其中一个平面内的一条直线垂直于另一个平面即可(两个平面垂直的判定定理)
需要证明这条直线与另一个平面内的两条相交直线垂直(直线和平面垂直的判定定理知).
本题中,利用直线与平面垂直的性质以及圆的性质易得所需条件.
环节三、例题讲解
∴PA⊥BC.
证明:∵PA⊥平面ABC,BC ?平面ABC,
?
∵点C是圆周上不同于A,B的任意一点,
且AB是☉O的直径,
∴∠ACB=90°,即BC⊥AC.
又∵ PA ∩ AC=A,PA、AC ?平面PAC,
?
∴BC⊥平面PAC.
∴平面PAC ⊥平面PBC.
又∵BC ?平面PBC,
?
环节四、习题练习
5min完成练习1~4
1. 如图,检查工件的相邻两个(平)面是否垂直时,只要用曲尺的一边
紧靠在工件的一个面上,另一边在工件的另一个面上转动,观察尺边和
这个面是否密合就可以了.这是为什么?
答:由面面垂直的判定定理可知:转动时,如果尺边
与这个面密合,则说明另一尺边垂直于这个面,于是
工件的相邻两个面互相垂直.
环节四、习题练习
2.已知直线????,????与平面????,????,????,能使????⊥????的充分条件是( )
A. ????⊥????,????⊥???? B. ????∩??=????,????⊥????,?????????
C. ????//????,????//???? D. ????//????,????⊥????
?
分析:A. 不正确,反例如图所示.
B. 由 ????∩????=????,????⊥????,不能推出????⊥????,所以也不能推出????⊥????.
?
C. 由 ????//????,????//????可得,????//????,或????∩????=????且????//????,但????⊥????不一定成立.
?
环节四、习题练习
2.已知直线????,????与平面????,????,????,能使????⊥????的充分条件是( )
A. ????⊥????,????⊥???? B. ????∩????=????,????⊥????,?????????
C. ????//????,????//???? D. ????//????,????⊥????
?
分析:
D. ∵????//????,∴可以过直线????做一平面????∩????=????,则????//????.
?
∵????⊥????,∴????⊥????.
?
∵直线?????????,∴????⊥????.
?
D
环节四、习题练习
3.如图,????????⊥平面????????????,????????⊥????????,你能发现哪些平面互相垂直,为什么?
?
∵????????⊥平面????????????,?????????平面????????????,∴平面????????????⊥平面????????????.
?
同理,平面????????????⊥平面????????????.
?
∵????????⊥平面????????????,?????????平面????????????
∴????????⊥????????.
?
∵????????⊥????????,∴????????⊥平面????????????.
?
∵?????????平面??????????,∴平面????????????⊥平面????????????.
?
答:平面????????????⊥平面????????????,平面????????????⊥平面????????????,平面????????????⊥平面????????????.
?
环节四、习题练习
4.如图,在正三棱柱?????????????????′????′????′中,????为棱????????的中点.
求证:平面????????????′⊥平面????????????′????′.
?
证明:∵?????????????????′????′????′是正三棱柱,∴????????′⊥平面????????????.
?
(正三棱柱的定义)
∵?????????平面????????????,∴????????′⊥????????.
?
(线面垂直的定义)
∵△????????????是正三角形,????为????????的中点,∴????????⊥????????.
?
(平面几何知识)
∵????????∩????????′=????,∴????????⊥平面????????????′????′.
?
(线面垂直的判定)
∵?????????平面????????????′,∴平面????????????′⊥平面????????????′????′.
?
(面面垂直的判定)
方法收获
知识收获
环节五、归纳总结
2.(选做题)研究性作业
1.(必做题)
完成课本第163页,习题8.6的第7、8题
观察生活中的面面垂直关系,结合本节课的探究经验,你还能有其它进一步的认识吗?
请试着将空间中的线面垂直关系形成体系,绘制一个思维导图.
下节,精彩继续……
重庆市南开中学 赵爽
谢 谢
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
