二次根式的概念与性质
图片预览






文档简介
(共15张PPT)
第十七章二次根式
学校:肥东六中
班级: 八 (1)
教师: 谢 俊
时间:12- 03- 12
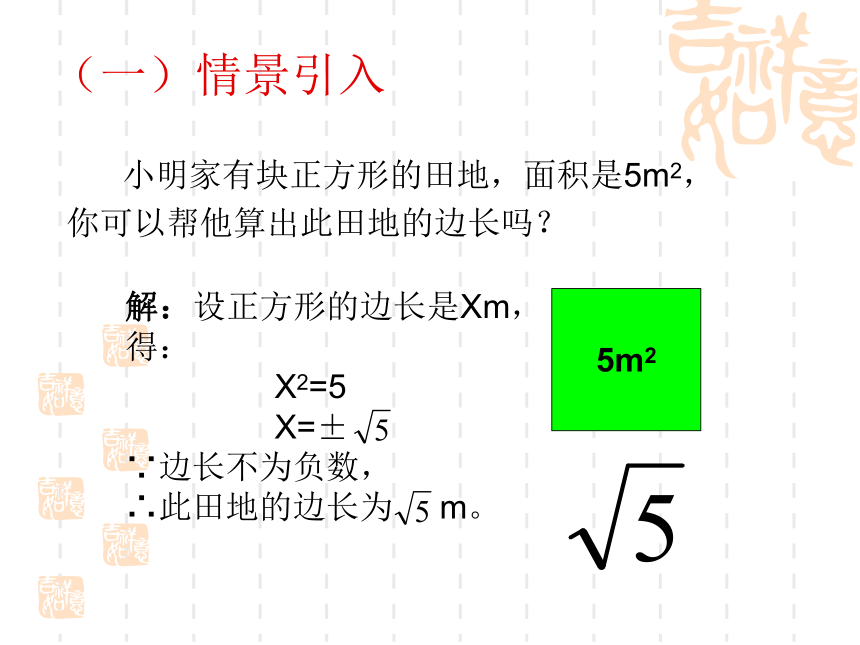
(一)情景引入
小明家有块正方形的田地,面积是5m2,
你可以帮他算出此田地的边长吗?
5m2
解:设正方形的边长是Xm,得:
X2=5
X=±
∵边长不为负数,
∴此田地的边长为 m。
(二)内容讲解
1.二次根式:
形如 (a ≥0 )的式子,叫做二次根式。
它应满足:
(1)含有二次根号( )。
(2)被开方数a≥0。
例1:判断下列式子是否是二次根式
(三)观察思考
2二次根式的性质:
(1)我们知道 是2的算术平方根,根据平方根的意义,应用( )2=2,类似地,计算:
( )2= ( )2=
( )2=
性质1:( )2=a(a≥0)
5
0
(2) = =3,类似地,计算:
=____ =____ =_____
又如 = =3=-(-3),再计算:
=____ =_____
性质2: =︱a︱=
{
a (a≥0)
-a (a <0)
0.5
0
0.5
(四)例题分析
例2 X为何值时,下列式子在实数范围内有意义?
(1) (2) (3)
解:(1)要使有意义,必须X+3≥0,
解这个不等式,得 X≥-3
即当X≥-3时,有意义。
(2) 因为 X为任何实数时都有X2 ≥0
所以当X为一切实数时,都有意义。
(3)因为X ≥0,同时-X ≥0,即X≤0,
所以,要使根式同时有意义,必须X=0
即当X=0时,有意义。
例3 计算:
(1) (2)
解: (1)
(2)
例4 已知 ,求a和b的值。
注: a2≥0
︱a︱≥0
≥0
∴
解:∵ ≥0, ≥0.
a-b-1=0
2a-b=0
解此方程组,得: a=-1
b=-2
∴a的值为-1,b的值为-2
(五)巩固练习
1.求下列各式的值:
(1)( )2 (2)(- )2
(3)-
(4)-
= 0.8
= -︱2︱
=-2
=- ︱-2︱
=-2
2.已知 + ︱y-3︱+(z+4)2=0,求y x- z的值。
解:∵ x-2=0 ∴ y x- z=32-(-4)
y-3=0 =9+4
z+4=0 =13
∴ x=2
y=3
z=-4
(六)课堂小结
1.二次根式的定义:
形如 (a ≥0 )的式子,叫做二次根式。
{
a (a≥0)
-a (a <0)
2.二次根式的性质:
性质1:( )2=a(a≥0)
性质2: =︱a︱=
(七)作业布置
课本P6习题17.1第4,5题
(完)
第十七章二次根式
学校:肥东六中
班级: 八 (1)
教师: 谢 俊
时间:12- 03- 12
(一)情景引入
小明家有块正方形的田地,面积是5m2,
你可以帮他算出此田地的边长吗?
5m2
解:设正方形的边长是Xm,得:
X2=5
X=±
∵边长不为负数,
∴此田地的边长为 m。
(二)内容讲解
1.二次根式:
形如 (a ≥0 )的式子,叫做二次根式。
它应满足:
(1)含有二次根号( )。
(2)被开方数a≥0。
例1:判断下列式子是否是二次根式
(三)观察思考
2二次根式的性质:
(1)我们知道 是2的算术平方根,根据平方根的意义,应用( )2=2,类似地,计算:
( )2= ( )2=
( )2=
性质1:( )2=a(a≥0)
5
0
(2) = =3,类似地,计算:
=____ =____ =_____
又如 = =3=-(-3),再计算:
=____ =_____
性质2: =︱a︱=
{
a (a≥0)
-a (a <0)
0.5
0
0.5
(四)例题分析
例2 X为何值时,下列式子在实数范围内有意义?
(1) (2) (3)
解:(1)要使有意义,必须X+3≥0,
解这个不等式,得 X≥-3
即当X≥-3时,有意义。
(2) 因为 X为任何实数时都有X2 ≥0
所以当X为一切实数时,都有意义。
(3)因为X ≥0,同时-X ≥0,即X≤0,
所以,要使根式同时有意义,必须X=0
即当X=0时,有意义。
例3 计算:
(1) (2)
解: (1)
(2)
例4 已知 ,求a和b的值。
注: a2≥0
︱a︱≥0
≥0
∴
解:∵ ≥0, ≥0.
a-b-1=0
2a-b=0
解此方程组,得: a=-1
b=-2
∴a的值为-1,b的值为-2
(五)巩固练习
1.求下列各式的值:
(1)( )2 (2)(- )2
(3)-
(4)-
= 0.8
= -︱2︱
=-2
=- ︱-2︱
=-2
2.已知 + ︱y-3︱+(z+4)2=0,求y x- z的值。
解:∵ x-2=0 ∴ y x- z=32-(-4)
y-3=0 =9+4
z+4=0 =13
∴ x=2
y=3
z=-4
(六)课堂小结
1.二次根式的定义:
形如 (a ≥0 )的式子,叫做二次根式。
{
a (a≥0)
-a (a <0)
2.二次根式的性质:
性质1:( )2=a(a≥0)
性质2: =︱a︱=
(七)作业布置
课本P6习题17.1第4,5题
(完)
