2020-2021初中数学北师版七年级下册同步课件1.5 平方差公式(第1课时 23张)
文档属性
| 名称 | 2020-2021初中数学北师版七年级下册同步课件1.5 平方差公式(第1课时 23张) |  | |
| 格式 | pptx | ||
| 文件大小 | 245.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 21:14:52 | ||
图片预览








文档简介
1.5 平方差公式(第1课时)
北师大版 数学 七年级 下册
王敏同学去商店买了单价是9.8元/千克的糖果10.2千克,售货员刚拿起计算器,王敏就说出应付99.96元,结果与售货员计算出的结果相吻合.售货员很惊讶地说:“你好像是个神童,怎么算得这么快?”
王敏同学说:“过奖了,我利用了在数学上刚学过的一个公式.”
你知道王敏同学用的是一个什么样的公式吗?
导入新知
1. 了解平方差公式的推导过程,掌握平方差公式.
2. 能利用平方差公式进行计算.
素养目标
3. 培养学生观察能力和符号意识.
计算下列各题:
(1)( x+2 ) ( x-2 ); (2)( 1+ 3a ) (1- 3a );
(3)( x+5y) ( x-5y );(4)( 2y+z ) (2y- z ).
(1)x2 -4 ;
探究新知
知识点
平方差公式
思考:1、观察算式结构,你发现了什么规律?
2、计算结果后,你又发现了什么规律?
(2)1- 9a2;
(3)x2-25y 2;
(4)4y2 - z2 .
(a+b)(a?b)=
a2?b2
两数和与这两数差的积,等于这两数的平方差.
公式变形:
1.(a – b ) ( a + b) = a2 - b2
2.(b + a )( -b + a ) = a2 - b2
平方差公式
探究新知
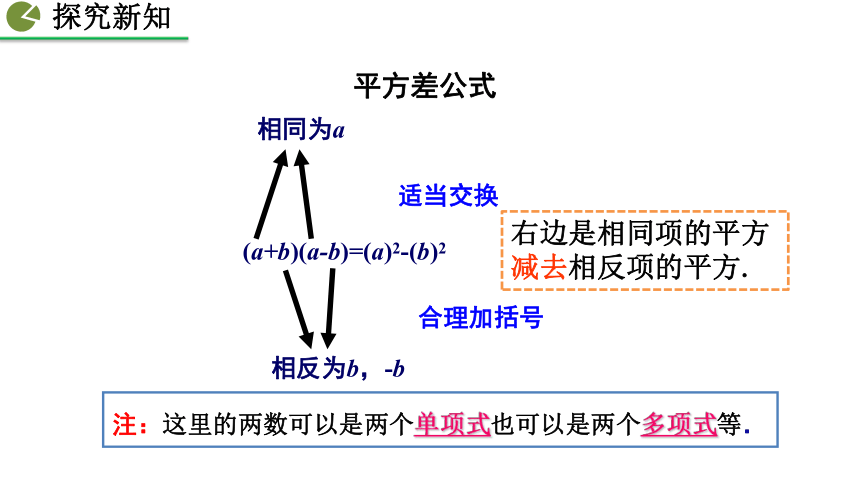
平方差公式
注:这里的两数可以是两个单项式也可以是两个多项式等.
(a+b)(a-b)=(a)2-(b)2
相同为a
相反为b,-b
适当交换
合理加括号
探究新知
右边是相同项的平方减去相反项的平方.
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
填一填:
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
探究新知
练一练:口答下列各题:
(1)(-a+b)(a+b)=_________.
(2)(a-b)(b+a)= __________.
(3)(-a-b)(-a+b)= ________.
(4)(a-b)(-a-b)= _________.
a2-b2
a2-b2
b2-a2
b2-a2
探究新知
探究新知
利用平方差公式计算:(1)( 5+ 6x) ( 5-6x);
(2)( x-2y) ( x+2y); (3)(- m+n) (-m-n)
例1
解:(1)( 5 + 6 x) ( 5- 6 x) = 52 - ( 6 x )2
(2)( x - 2y ) ( x + 2 y ) = x2 - ( 2 y )2
(3)( -m+n ) ( -m-n ) = ( - m )2 - n2
素养考点 1
利用平方差公式进行运算
= 25- 36x2;
= x2 - 4y2;
= m2 -n2.
方法总结
探究新知
应用平方差公式计算时,应注意以下几个问题:
(1)左边是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数;
(2)右边是相同项的平方减去相反项的平方;
(3)公式中的a和b可以是具体数,也可以是单项式或多项式.
利用平方差公式计算:
(1)(3x-5)(3x+5); (2)(-2a-b)(b-2a);
(3)(-7m+8n)(-8n-7m).
解:(1)原式=(3x)2-52=9x2-25;
(2)原式=(-2a)2-b2=4a2-b2;
(3)原式=(-7m)2-(8n)2=49m2-64n2;
巩固练习
变式训练
探究新知
利用平方差公式计算:
(1) ;
(2)( ab + 8 ) ( ab - 8 ).
例2
解:
(1)
(2)( ab + 8 ) ( ab - 8 )= (ab)2- 64
= a2b2- 64 .
(2)(a+3)(a2+9)(a-3).
计算:
巩固练习
变式训练
(2)原式=(a+3)(a-3)(a2+9)
=(a2-9)(a2+9)
=(a2)2-92
=a4-81.
解:(1)
例3 先化简,再求值:(2x-y)(y+2x)-(2y+x)(2y-x),其中x=1,y=2.
解:原式=4x2-y2-(4y2-x2)
原式=5×12-5×22=-15.
=4x2-y2-4y2+x2
=5x2-5y2.
当x=1,y=2时,
探究新知
利用平方差公式进行化简求值
素养考点 2
先化简,再求值:(3-x)(3+x)+2(x+1)(x-1),其中x=2.
巩固练习
解:(3-x)(3+x)+2(x+1)(x-1)
=9-x2+2(x2-1)
=9-x2+2x2-2
=7+x2
当x=2时,
原式=7+22
=7+4
=11
变式训练
1.(2020?杭州)(1+y)(1﹣y)=( )
A.1+y2 B.﹣1﹣y2 C.1﹣y2 D.﹣1+y2
2.(2020?临沂)若a+b=1,则a2﹣b2+2b﹣2= .
C
-1
连接中考
1.下列运算中,可用平方差公式计算的是( )
A.(x+y)(x+y) B.(-x+y)(x-y)
C.(-x-y)(y-x) D.(x+y)(-x-y)
C
2.计算(2x+1)(2x-1)等于( )
A.4x2-1 B.2x2-1 C.4x-1 D.4x2+1
A
3.两个正方形的边长之和为5,边长之差为2,那么用较大的正方形的面积减去较小的正方形的面积,差是________.
10
基础巩固题
课堂检测
(1)(a+3b)(a- 3b);
=4a2-9;
=4x4-y2.
解:原式=(2a+3)(2a-3)
=a2-9b2 ;
=(2a)2-32
解:原式=(-2x2 )2-y2
解:原式=(a)2-(3b)2
(2)(3+2a)(-3+2a);
(3)(-2x2-y)(-2x2+y).
4.利用平方差公式计算:
基础巩固题
课堂检测
先化简,再求值:(x+1)(x-1)+x2(1-x)+x3,其中x=2.
解:原式=x2-1+x2-x3+x3
=2x2-1.
将x=2代入上式,
原式=2×22-1=7.
能力提升题
课堂检测
已知x≠1,计算:(1+x)(1-x)=1-x2,(1-x)(1+x+x2)=1-x3,(1-x)(1+x+x2+x3)=1-x4
(1)观察以上各式并猜想:(1-x)(1+x+x2+…+xn)=________;(n为正整数)
(2)根据你的猜想计算:
①(1-2)(1+2+22+23+24+25)=________;
②2+22+23+…+2n=________(n为正整数);
③(x-1)(x99+x98+x97+…+x2+x+1)=________;
1-xn+1
-63
2n+1-2
x100-1
课堂检测
拓广探索题
(3)通过以上规律请你进行下面的探索:
①(a-b)(a+b)=________;
②(a-b)(a2+ab+b2)=________;
③(a-b)(a3+a2b+ab2+b3)=________.
a2-b2
a3-b3
a4-b4
课堂检测
平方差公式
内容
注意
两个数的和与这两个数的差的积,等于这两个数的平方差
符号表示:(a+b)(a-b)=a2-b2
紧紧抓住 “一同一反”这一特征,在应用时,只有两个二项式的积才有可能应用平方差公式;对于不能直接应用公式的,可能要经过变形才可以应用
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
北师大版 数学 七年级 下册
王敏同学去商店买了单价是9.8元/千克的糖果10.2千克,售货员刚拿起计算器,王敏就说出应付99.96元,结果与售货员计算出的结果相吻合.售货员很惊讶地说:“你好像是个神童,怎么算得这么快?”
王敏同学说:“过奖了,我利用了在数学上刚学过的一个公式.”
你知道王敏同学用的是一个什么样的公式吗?
导入新知
1. 了解平方差公式的推导过程,掌握平方差公式.
2. 能利用平方差公式进行计算.
素养目标
3. 培养学生观察能力和符号意识.
计算下列各题:
(1)( x+2 ) ( x-2 ); (2)( 1+ 3a ) (1- 3a );
(3)( x+5y) ( x-5y );(4)( 2y+z ) (2y- z ).
(1)x2 -4 ;
探究新知
知识点
平方差公式
思考:1、观察算式结构,你发现了什么规律?
2、计算结果后,你又发现了什么规律?
(2)1- 9a2;
(3)x2-25y 2;
(4)4y2 - z2 .
(a+b)(a?b)=
a2?b2
两数和与这两数差的积,等于这两数的平方差.
公式变形:
1.(a – b ) ( a + b) = a2 - b2
2.(b + a )( -b + a ) = a2 - b2
平方差公式
探究新知
平方差公式
注:这里的两数可以是两个单项式也可以是两个多项式等.
(a+b)(a-b)=(a)2-(b)2
相同为a
相反为b,-b
适当交换
合理加括号
探究新知
右边是相同项的平方减去相反项的平方.
(1+x)(1-x)
(-3+a)(-3-a)
(0.3x-1)(1+0.3x)
(1+a)(-1+a)
填一填:
a
b
a2-b2
1
x
-3
a
12-x2
(-3)2-a2
a
1
a2-12
0.3x
1
( 0.3x)2-12
(a-b)(a+b)
探究新知
练一练:口答下列各题:
(1)(-a+b)(a+b)=_________.
(2)(a-b)(b+a)= __________.
(3)(-a-b)(-a+b)= ________.
(4)(a-b)(-a-b)= _________.
a2-b2
a2-b2
b2-a2
b2-a2
探究新知
探究新知
利用平方差公式计算:(1)( 5+ 6x) ( 5-6x);
(2)( x-2y) ( x+2y); (3)(- m+n) (-m-n)
例1
解:(1)( 5 + 6 x) ( 5- 6 x) = 52 - ( 6 x )2
(2)( x - 2y ) ( x + 2 y ) = x2 - ( 2 y )2
(3)( -m+n ) ( -m-n ) = ( - m )2 - n2
素养考点 1
利用平方差公式进行运算
= 25- 36x2;
= x2 - 4y2;
= m2 -n2.
方法总结
探究新知
应用平方差公式计算时,应注意以下几个问题:
(1)左边是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数;
(2)右边是相同项的平方减去相反项的平方;
(3)公式中的a和b可以是具体数,也可以是单项式或多项式.
利用平方差公式计算:
(1)(3x-5)(3x+5); (2)(-2a-b)(b-2a);
(3)(-7m+8n)(-8n-7m).
解:(1)原式=(3x)2-52=9x2-25;
(2)原式=(-2a)2-b2=4a2-b2;
(3)原式=(-7m)2-(8n)2=49m2-64n2;
巩固练习
变式训练
探究新知
利用平方差公式计算:
(1) ;
(2)( ab + 8 ) ( ab - 8 ).
例2
解:
(1)
(2)( ab + 8 ) ( ab - 8 )= (ab)2- 64
= a2b2- 64 .
(2)(a+3)(a2+9)(a-3).
计算:
巩固练习
变式训练
(2)原式=(a+3)(a-3)(a2+9)
=(a2-9)(a2+9)
=(a2)2-92
=a4-81.
解:(1)
例3 先化简,再求值:(2x-y)(y+2x)-(2y+x)(2y-x),其中x=1,y=2.
解:原式=4x2-y2-(4y2-x2)
原式=5×12-5×22=-15.
=4x2-y2-4y2+x2
=5x2-5y2.
当x=1,y=2时,
探究新知
利用平方差公式进行化简求值
素养考点 2
先化简,再求值:(3-x)(3+x)+2(x+1)(x-1),其中x=2.
巩固练习
解:(3-x)(3+x)+2(x+1)(x-1)
=9-x2+2(x2-1)
=9-x2+2x2-2
=7+x2
当x=2时,
原式=7+22
=7+4
=11
变式训练
1.(2020?杭州)(1+y)(1﹣y)=( )
A.1+y2 B.﹣1﹣y2 C.1﹣y2 D.﹣1+y2
2.(2020?临沂)若a+b=1,则a2﹣b2+2b﹣2= .
C
-1
连接中考
1.下列运算中,可用平方差公式计算的是( )
A.(x+y)(x+y) B.(-x+y)(x-y)
C.(-x-y)(y-x) D.(x+y)(-x-y)
C
2.计算(2x+1)(2x-1)等于( )
A.4x2-1 B.2x2-1 C.4x-1 D.4x2+1
A
3.两个正方形的边长之和为5,边长之差为2,那么用较大的正方形的面积减去较小的正方形的面积,差是________.
10
基础巩固题
课堂检测
(1)(a+3b)(a- 3b);
=4a2-9;
=4x4-y2.
解:原式=(2a+3)(2a-3)
=a2-9b2 ;
=(2a)2-32
解:原式=(-2x2 )2-y2
解:原式=(a)2-(3b)2
(2)(3+2a)(-3+2a);
(3)(-2x2-y)(-2x2+y).
4.利用平方差公式计算:
基础巩固题
课堂检测
先化简,再求值:(x+1)(x-1)+x2(1-x)+x3,其中x=2.
解:原式=x2-1+x2-x3+x3
=2x2-1.
将x=2代入上式,
原式=2×22-1=7.
能力提升题
课堂检测
已知x≠1,计算:(1+x)(1-x)=1-x2,(1-x)(1+x+x2)=1-x3,(1-x)(1+x+x2+x3)=1-x4
(1)观察以上各式并猜想:(1-x)(1+x+x2+…+xn)=________;(n为正整数)
(2)根据你的猜想计算:
①(1-2)(1+2+22+23+24+25)=________;
②2+22+23+…+2n=________(n为正整数);
③(x-1)(x99+x98+x97+…+x2+x+1)=________;
1-xn+1
-63
2n+1-2
x100-1
课堂检测
拓广探索题
(3)通过以上规律请你进行下面的探索:
①(a-b)(a+b)=________;
②(a-b)(a2+ab+b2)=________;
③(a-b)(a3+a2b+ab2+b3)=________.
a2-b2
a3-b3
a4-b4
课堂检测
平方差公式
内容
注意
两个数的和与这两个数的差的积,等于这两个数的平方差
符号表示:(a+b)(a-b)=a2-b2
紧紧抓住 “一同一反”这一特征,在应用时,只有两个二项式的积才有可能应用平方差公式;对于不能直接应用公式的,可能要经过变形才可以应用
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
