2020-2021初中数学北师版七年级下册同步课件6.3 等可能事件的概率(第4课时)【PPT版】
文档属性
| 名称 | 2020-2021初中数学北师版七年级下册同步课件6.3 等可能事件的概率(第4课时)【PPT版】 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 20:46:03 | ||
图片预览







文档简介
6.3 等可能事件的概率(第4课时)
北师大版 数学 七年级 下册
如图是一个转盘,小颖认为转盘上共有三种不同的颜色,所以自由转动这个转盘,指针停在红色、黄色、或蓝色区域的概率都是 你认为呢?
导入新知
1. 通过试验让学生理解转盘中概率的计算方法.
2. 能利用转盘解答简单的概率问题.
素养目标
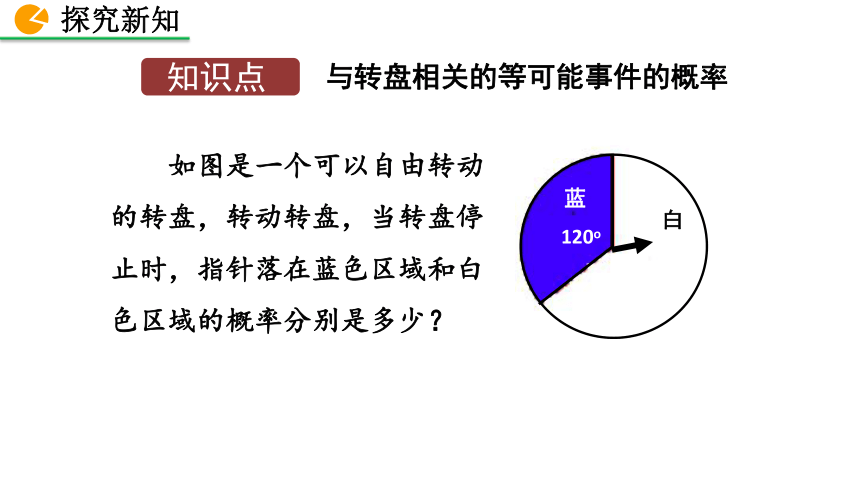
如图是一个可以自由转动的转盘,转动转盘,当转盘停止时,指针落在蓝色区域和白色区域的概率分别是多少?
知识点
与转盘相关的等可能事件的概率
探究新知
120o
白
蓝
指针不是落在蓝色区域就是落在白色区域,落在蓝色区域和白色区域的概率相等,所以P(落在蓝色区域)=P(落在白色区域)=
探究新知
白
蓝
120o
白1
蓝
探究新知
白2
先把白色区域等分成2份,这样转盘被分成3个扇形区域,其中1个是蓝色,2个是白色,所以P(落在蓝色区域)=
P(落在白色区域) =
120o
120o
白
蓝
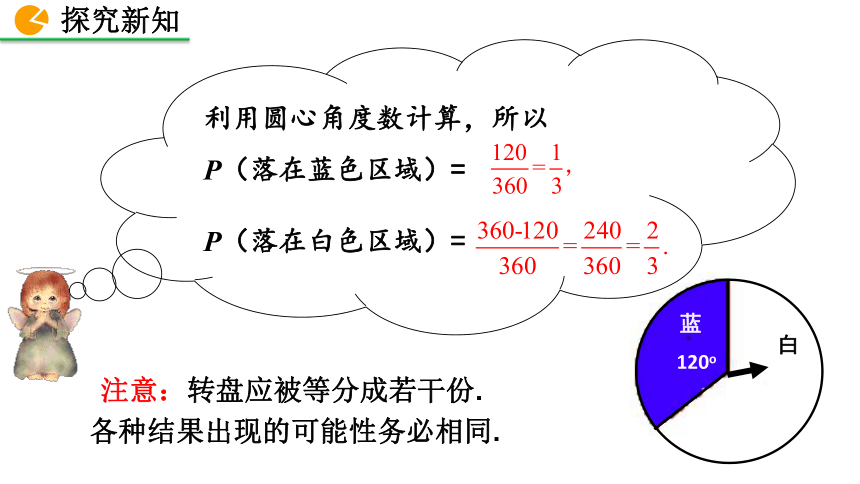
利用圆心角度数计算,所以
P(落在蓝色区域)=
P(落在白色区域)=
注意:转盘应被等分成若干份.
各种结果出现的可能性务必相同.
探究新知
转动如图所示的转盘,当转盘停止时,指针落在红色区域和蓝色区域的概率分别是多少?
想一想:
110o
红
蓝
探究新知
P(红)=
2536,
?
P(蓝)=
1136.
?
某路口南北方向红绿灯的设置时间为:红灯40s、绿灯60s、黄灯3s.小明的爸爸随机地由南往北开车到达该路口,问:
(1)他遇到红灯的概率大还是遇到绿灯的概率大?
(2)他遇到红灯的概率是多少?
探究新知
素养考点 1
时间有关的概率问题
例1
解:(1)小明的爸爸随机地到达该路口,他每一时刻到达的可能性都相同.因为该路口南北方向红绿灯的设置时间为:红灯40s,绿灯60s,黄灯3s.绿灯时间比红灯时间长,所以他遇到绿灯的概率大.
(2)他遇到红灯的概率为:
探究新知
1.如图,是圆形飞镖转盘,任意掷一飞镖,飞镖最可能落的区域是( )
A.红色区域 B.黑色区域
C.白色区域 D.紫色区域
2.下列抽奖转盘设计各中奖机会均等的是( )
A
C
巩固练习
变式训练
例2 如图所示,转盘被等分成八个扇形,并在上面依次标有数字1,2,3,4,5,6,7,8.
(1)自由转动转盘,当它停止转动时,指针指向的数正好能被8整除的概率是多少?
(2)请你用这个转盘设计一个游戏,当自由
转动的转盘停止时,指针指向的区域的概率为 .
(注:指针指在边缘处,要重新转,直至指到非边缘处).
探究新知
素养考点 2
转盘中的概率问题
34
?
解:(1)根据题意分析可得:转盘被等分成八个扇形,并在上面依次标有数字1,2,3,4,5,6,7,8;
正好能被8整除的有1个,故自由转动转盘,当它停止转动时,指针指向的数正好能被8整除的概率是 ;
(2)根据随机事件概率的求法:当自由转动的转盘停止时,指针指向的区域的概率为 ,只需是满足条件的区域有6个即可;如当自由转动转盘停止时,指针指向区域的数小于7的概率(答案不唯一).
探究新知
34
?
18
?
如图所示,转盘被等分成六个扇形,并在上面依次写上数字1,2,3,4,5,6;
(1)若自由转动转盘,当它停止转动时,指针指向偶数区的概率是多少?
(2)请你用这个转盘设计一个游戏,当自由转动的转盘停止时,指针指向的区域的概率为
解:(1)P(指针指向偶数区域)= ;
自由转动转盘,当它停止转动时,指针指向
偶数区的概率是 ;
巩固练习
变式训练
(2)方法一:如图所示,自由转动转盘,当转盘停止时,指针指向红色部分区域的概率为 ;
方法二:自由转动转盘,当它停止时,指针指向的数字不大于4时,指针指向的区域的概率是 .
巩固练习
(2020?衢州)如图是一个游戏转盘,自由转动转盘,当转盘停止转动后,指针落在数字“Ⅱ”所示区域内的概率是( )
A. B. C. D.
连接中考
A
1.如图是小鹏自己制作的正方形飞镖盘,并在盘内画了两个小正方形,则小鹏在投掷飞镖时,飞镖扎在阴影部分的概率为( )
A. B. C. D.
2.如图所示为一水平放置的转盘,使劲转动其指针,并让它自由停下,下面叙述正确的是( )
A.停在B区比停在A区的机会大
B.停在三个区的机会一样大
C.停在哪个区与转盘半径大小有关
D.停在哪个区是可以随心所欲的
A
A
课堂检测
基础巩固题
3.如图,把一个圆形转盘按1:2:3:4的比例分成A,B,C,D四个扇形区域,自由转动转盘,停止后指针落在C区域的概率是 .
解析:由题意可得:指针落在C区域的概率是: .
故答案为: .
课堂检测
基础巩固题
4.如图所示是一个转盘,转盘分成7个相同的扇形,颜色分为红黄绿三种,指针固定,转动转盘后任其自由停止,某个扇形会停在指针所指的位置,(指针指向交线时当作指向右边的扇形)求下列事件的概率.
(1)指向红色;
(2)指向红色或黄色;
(3)不指向红色.
课堂检测
基础巩固题
解:一共有7种等可能的结果.
(1)指向红色有3种结果,
P(指向红色)= ;
(2)指向红色或黄色一共有5种等可能的结果,P( 指向红或黄)= ;
(3)不指向红色有4种等可能的结果
P( 不指向红色)= .
课堂检测
5.如图是一个可以自由转动的转盘,标有黄色和蓝色区域的扇形圆心角分别是145°和45°,则随机转动转盘,指针在红色区域的概率是多少?
解:指针在红色区域的概率为P(红色)= ,
答:随机转动转盘,指针在红色区域的概率是 .
课堂检测
基础巩固题
设计一个转盘,使得自由转动这个转盘,指针停在红色区域中的概率为 .
解:根据几何概率的求法:指针停在有色区域的概率就是该色区域的面积与总面积的比值;即红色区域的面积与总面积的比值为 ,
故设计如下:把圆分成相等的6等份,红色占2份即可.
课堂检测
能力提升题
如图,一个转盘被平均分成12份,每份上写上不同的数字,游戏方法:先猜数后转动转盘,若指针指向的数字与所猜的数一致,则猜数者获胜.现提供三种猜数方法:
(1)猜是“奇数”,或是“偶数”.
(2)猜是“大于10的数”,或是“不大于10的数”.
(3)猜是“3的倍数”,或是“不是3的倍数”.
如果你是猜数者,你愿意选择哪一种猜数方法?怎样猜?并说明理由.
课堂检测
拓广探索题
解:选择第(3)种方法,猜是“3的倍数”,
因为转盘中,奇数与偶数的个数相同,大于10与不大于10的数的个数也相同,
所以(1)与(2)游戏是公平的,转盘中的数是3的倍数的有7个,不是3的倍数的有5个.
所以猜3的倍数,获胜的机会大.
课堂检测
该事件所占区域的面积
1.所求事件的概率= ————————————
总面积
2.各种结果出现的可能性务必相同.
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
北师大版 数学 七年级 下册
如图是一个转盘,小颖认为转盘上共有三种不同的颜色,所以自由转动这个转盘,指针停在红色、黄色、或蓝色区域的概率都是 你认为呢?
导入新知
1. 通过试验让学生理解转盘中概率的计算方法.
2. 能利用转盘解答简单的概率问题.
素养目标
如图是一个可以自由转动的转盘,转动转盘,当转盘停止时,指针落在蓝色区域和白色区域的概率分别是多少?
知识点
与转盘相关的等可能事件的概率
探究新知
120o
白
蓝
指针不是落在蓝色区域就是落在白色区域,落在蓝色区域和白色区域的概率相等,所以P(落在蓝色区域)=P(落在白色区域)=
探究新知
白
蓝
120o
白1
蓝
探究新知
白2
先把白色区域等分成2份,这样转盘被分成3个扇形区域,其中1个是蓝色,2个是白色,所以P(落在蓝色区域)=
P(落在白色区域) =
120o
120o
白
蓝
利用圆心角度数计算,所以
P(落在蓝色区域)=
P(落在白色区域)=
注意:转盘应被等分成若干份.
各种结果出现的可能性务必相同.
探究新知
转动如图所示的转盘,当转盘停止时,指针落在红色区域和蓝色区域的概率分别是多少?
想一想:
110o
红
蓝
探究新知
P(红)=
2536,
?
P(蓝)=
1136.
?
某路口南北方向红绿灯的设置时间为:红灯40s、绿灯60s、黄灯3s.小明的爸爸随机地由南往北开车到达该路口,问:
(1)他遇到红灯的概率大还是遇到绿灯的概率大?
(2)他遇到红灯的概率是多少?
探究新知
素养考点 1
时间有关的概率问题
例1
解:(1)小明的爸爸随机地到达该路口,他每一时刻到达的可能性都相同.因为该路口南北方向红绿灯的设置时间为:红灯40s,绿灯60s,黄灯3s.绿灯时间比红灯时间长,所以他遇到绿灯的概率大.
(2)他遇到红灯的概率为:
探究新知
1.如图,是圆形飞镖转盘,任意掷一飞镖,飞镖最可能落的区域是( )
A.红色区域 B.黑色区域
C.白色区域 D.紫色区域
2.下列抽奖转盘设计各中奖机会均等的是( )
A
C
巩固练习
变式训练
例2 如图所示,转盘被等分成八个扇形,并在上面依次标有数字1,2,3,4,5,6,7,8.
(1)自由转动转盘,当它停止转动时,指针指向的数正好能被8整除的概率是多少?
(2)请你用这个转盘设计一个游戏,当自由
转动的转盘停止时,指针指向的区域的概率为 .
(注:指针指在边缘处,要重新转,直至指到非边缘处).
探究新知
素养考点 2
转盘中的概率问题
34
?
解:(1)根据题意分析可得:转盘被等分成八个扇形,并在上面依次标有数字1,2,3,4,5,6,7,8;
正好能被8整除的有1个,故自由转动转盘,当它停止转动时,指针指向的数正好能被8整除的概率是 ;
(2)根据随机事件概率的求法:当自由转动的转盘停止时,指针指向的区域的概率为 ,只需是满足条件的区域有6个即可;如当自由转动转盘停止时,指针指向区域的数小于7的概率(答案不唯一).
探究新知
34
?
18
?
如图所示,转盘被等分成六个扇形,并在上面依次写上数字1,2,3,4,5,6;
(1)若自由转动转盘,当它停止转动时,指针指向偶数区的概率是多少?
(2)请你用这个转盘设计一个游戏,当自由转动的转盘停止时,指针指向的区域的概率为
解:(1)P(指针指向偶数区域)= ;
自由转动转盘,当它停止转动时,指针指向
偶数区的概率是 ;
巩固练习
变式训练
(2)方法一:如图所示,自由转动转盘,当转盘停止时,指针指向红色部分区域的概率为 ;
方法二:自由转动转盘,当它停止时,指针指向的数字不大于4时,指针指向的区域的概率是 .
巩固练习
(2020?衢州)如图是一个游戏转盘,自由转动转盘,当转盘停止转动后,指针落在数字“Ⅱ”所示区域内的概率是( )
A. B. C. D.
连接中考
A
1.如图是小鹏自己制作的正方形飞镖盘,并在盘内画了两个小正方形,则小鹏在投掷飞镖时,飞镖扎在阴影部分的概率为( )
A. B. C. D.
2.如图所示为一水平放置的转盘,使劲转动其指针,并让它自由停下,下面叙述正确的是( )
A.停在B区比停在A区的机会大
B.停在三个区的机会一样大
C.停在哪个区与转盘半径大小有关
D.停在哪个区是可以随心所欲的
A
A
课堂检测
基础巩固题
3.如图,把一个圆形转盘按1:2:3:4的比例分成A,B,C,D四个扇形区域,自由转动转盘,停止后指针落在C区域的概率是 .
解析:由题意可得:指针落在C区域的概率是: .
故答案为: .
课堂检测
基础巩固题
4.如图所示是一个转盘,转盘分成7个相同的扇形,颜色分为红黄绿三种,指针固定,转动转盘后任其自由停止,某个扇形会停在指针所指的位置,(指针指向交线时当作指向右边的扇形)求下列事件的概率.
(1)指向红色;
(2)指向红色或黄色;
(3)不指向红色.
课堂检测
基础巩固题
解:一共有7种等可能的结果.
(1)指向红色有3种结果,
P(指向红色)= ;
(2)指向红色或黄色一共有5种等可能的结果,P( 指向红或黄)= ;
(3)不指向红色有4种等可能的结果
P( 不指向红色)= .
课堂检测
5.如图是一个可以自由转动的转盘,标有黄色和蓝色区域的扇形圆心角分别是145°和45°,则随机转动转盘,指针在红色区域的概率是多少?
解:指针在红色区域的概率为P(红色)= ,
答:随机转动转盘,指针在红色区域的概率是 .
课堂检测
基础巩固题
设计一个转盘,使得自由转动这个转盘,指针停在红色区域中的概率为 .
解:根据几何概率的求法:指针停在有色区域的概率就是该色区域的面积与总面积的比值;即红色区域的面积与总面积的比值为 ,
故设计如下:把圆分成相等的6等份,红色占2份即可.
课堂检测
能力提升题
如图,一个转盘被平均分成12份,每份上写上不同的数字,游戏方法:先猜数后转动转盘,若指针指向的数字与所猜的数一致,则猜数者获胜.现提供三种猜数方法:
(1)猜是“奇数”,或是“偶数”.
(2)猜是“大于10的数”,或是“不大于10的数”.
(3)猜是“3的倍数”,或是“不是3的倍数”.
如果你是猜数者,你愿意选择哪一种猜数方法?怎样猜?并说明理由.
课堂检测
拓广探索题
解:选择第(3)种方法,猜是“3的倍数”,
因为转盘中,奇数与偶数的个数相同,大于10与不大于10的数的个数也相同,
所以(1)与(2)游戏是公平的,转盘中的数是3的倍数的有7个,不是3的倍数的有5个.
所以猜3的倍数,获胜的机会大.
课堂检测
该事件所占区域的面积
1.所求事件的概率= ————————————
总面积
2.各种结果出现的可能性务必相同.
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
