4.3 探索三角形全等的条件(第二课时)课件(共19张PPT)
文档属性
| 名称 | 4.3 探索三角形全等的条件(第二课时)课件(共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 00:00:00 | ||
图片预览



文档简介
1. 什么是全等三角形?
2. 我们已经学过了哪几种判定两个三角形全等的方法?
能够完全重合的两个三角形叫做全等三角形.
边边边(SSS).
3.如果已知一个三角形的两角及一边,
那么有几种可能的情况呢?
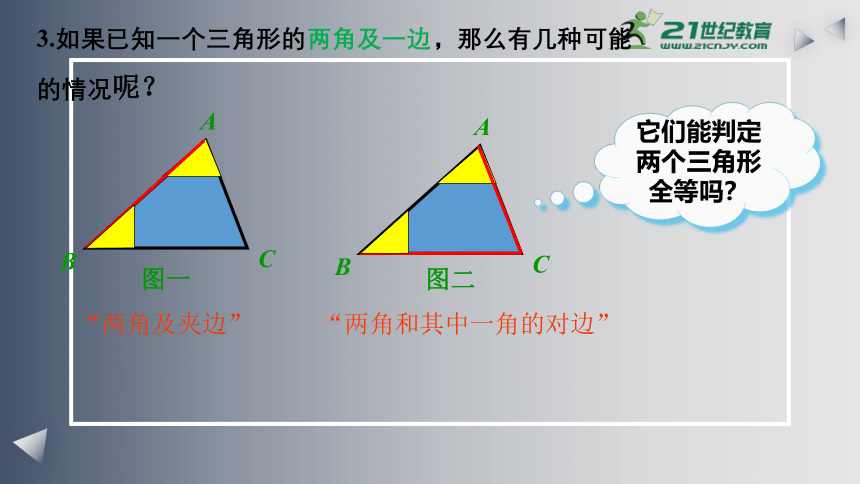
3.如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
A
B
C
A
B
C
图一
图二
“两角及夹边”
“两角和其中一角的对边”
它们能判定两个三角形全等吗?
3 第2课时
利用“ASA””AAS”判定三角形全等
有一块三角形纸片撕去了一个角,要去剪一块新的,如果你手头没有测量的仪器,你能保证新剪的纸片形状、大小和原来的一样吗?
【思考】 判别三角形全等是不是还有其他方法呢?
讲解新知
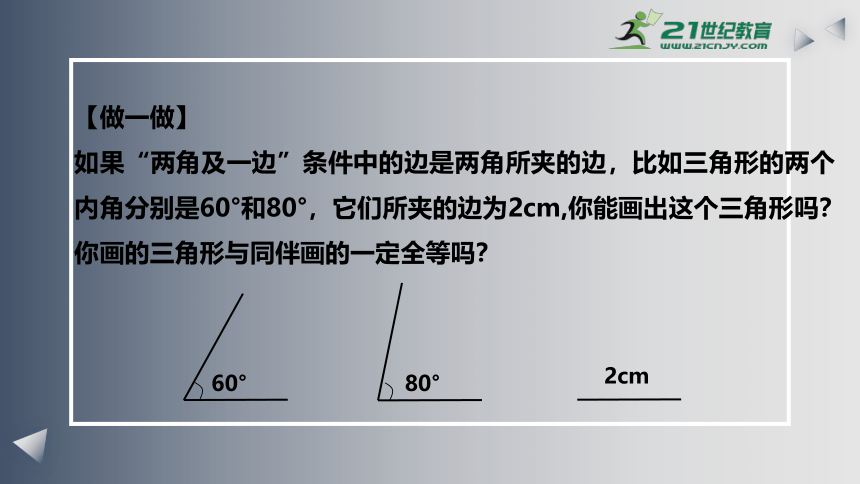
【做一做】
如果“两角及一边”条件中的边是两角所夹的边,比如三角形的两个内角分别是60°和80°,它们所夹的边为2cm,你能画出这个三角形吗?你画的三角形与同伴画的一定全等吗?
2cm
80°
60°
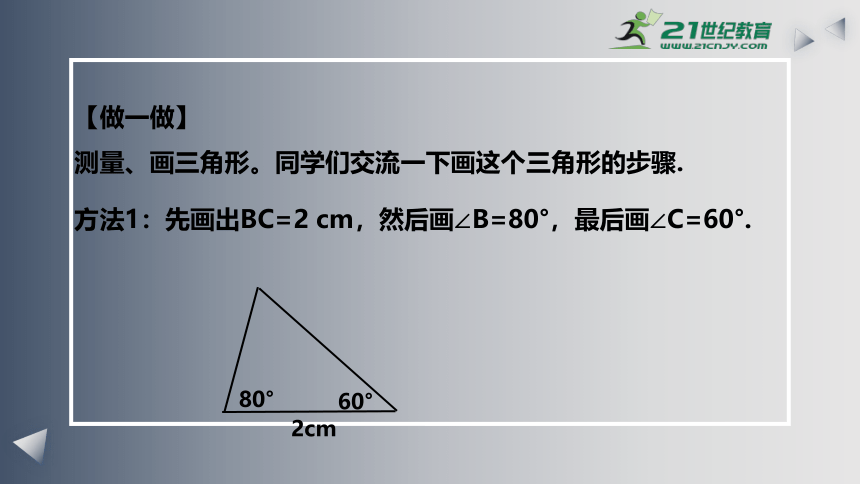
【做一做】
测量、画三角形。同学们交流一下画这个三角形的步骤.
2cm
80°
60°
方法1:先画出BC=2 cm,然后画∠B=80°,最后画∠C=60°.
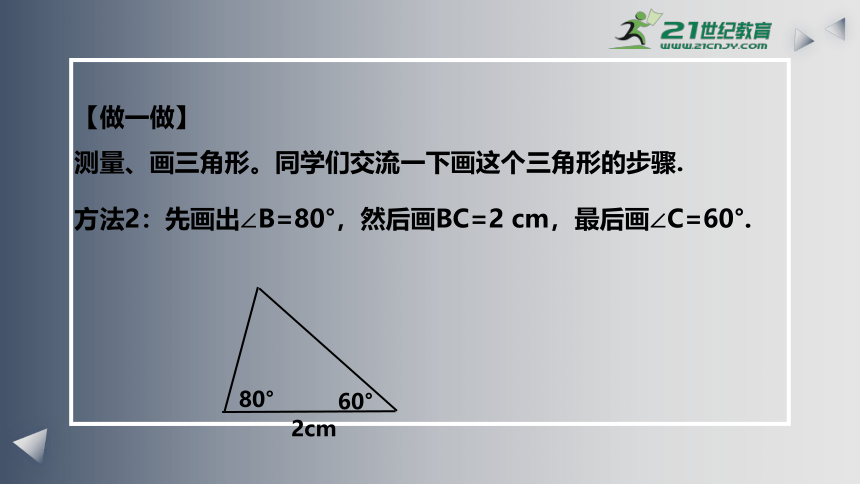
【做一做】
测量、画三角形。同学们交流一下画这个三角形的步骤.
2cm
80°
60°
方法2:先画出∠B=80°,然后画BC=2 cm,最后画∠C=60°.
改变角度和边长,你能得到同样的结论吗?
改变角度和边长,所画的三角形仍然全等。
同学把画出的三角形剪下来,与同小组比较,看是否重合.
画出的三角形都全等.
【总结归纳】
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
在△ABC和△DEF中,
∠A=∠D,
AB=DE,
∠B=∠E ,
∴△ABC≌△DEF(ASA).
几何语言:
A
B
C
D
E
F
例1 如图,点D在AB上,点E在AC上,AB=AC, ∠B=∠C,试说明:△ACD≌△ABE.
A
B
C
D
E
解:在△ACD和△ABE中,
∠A=∠A(公共角 ),
AC=AB(已知),
∠C=∠B (已知 ),
∴ △ACD≌△ABE(ASA),
例2 已知:如图,点B,F,C,E在一条直线上,∠A=∠D,AC=DF,且AC∥DF.
试说明:△ABC≌△DEF.
解:∵AC∥DF,
∴∠ACB=∠DFE.
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
∠A=∠D(已知 ),
AC=DF(已知),
∠ACB=∠DFE (已证 ),
1.如图,AB∥FC,DE=EF,AB=15,CF=8,则BD等于( )。
A .8
B .7
C .6
D .5
A
B
C
D
E
F
B
随堂练习
2.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,BE与AD交于点F,AD=BD=5,则AF+CD的长度为( )
A. 10
B. 6
C. 5
D. 4.5
C
A
B
C
D
E
F
1
2
A
B
C
D
3.如图,在△ABC 中 ,∠B=∠C,AD是∠BAC的角平分线,那么AB=AC吗?为什么?
证明:∵ AD是∠BAC的角平分线
∴ AB=AC(全等三角形对应边相等)
∴ ∠ 1=∠2 (角平分线定义)
在△ABD与△ACD中
∴ △ABD≌△ACD(ASA)
∠1= ∠2 (已证)
∠B=∠C (已知)
AD=AD (公共边)
4.如图,AD∥BC,BE∥DF,AE=CF,试说明:△ADF≌△CBE.
解:∵AD∥BC,BE∥DF,
∴∠A=∠C,∠DFE=∠BEC.
∵AE=CF,∴AE+EF=CF+EF,
即AF=CE.
在ADF和△CBE中,
∵
∴△ADF≌△CBE(ASA).
∠A= ∠C
AF=CE
∠DFA= ∠BEC
本节课我们经历了对符合两角一边的条件的所有三角形进行画图验证,探索出三角形全等的另一种方法,它是:
两角和它们的夹边对应相等的两个三角形全等(ASA)
再加上前面学的(SSS),证明两个三角形全等共有两种方法,我们要学会根据题目给出的条件选用合适的定理来证明两个三角形全等。
角边角:两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
在△ABC和△DEF中,
∠A=∠D,
AB=DE,
∠B=∠E ,
∴△ABC≌△DEF(ASA).
A
B
C
D
E
F
小结
三角形全等的判定
三角形全等的“ASA”判定:
两角及其夹边分别相等的两个三角形全等.
三角形全等的“AAS”判定:
两角分别相等且其中一组等角的对边相等的两个三角形全等.
注意两角与边位置关系的区别
https://www.21cnjy.com/help/help_extract.php
2. 我们已经学过了哪几种判定两个三角形全等的方法?
能够完全重合的两个三角形叫做全等三角形.
边边边(SSS).
3.如果已知一个三角形的两角及一边,
那么有几种可能的情况呢?
3.如果已知一个三角形的两角及一边,那么有几种可能的情况呢?
A
B
C
A
B
C
图一
图二
“两角及夹边”
“两角和其中一角的对边”
它们能判定两个三角形全等吗?
3 第2课时
利用“ASA””AAS”判定三角形全等
有一块三角形纸片撕去了一个角,要去剪一块新的,如果你手头没有测量的仪器,你能保证新剪的纸片形状、大小和原来的一样吗?
【思考】 判别三角形全等是不是还有其他方法呢?
讲解新知
【做一做】
如果“两角及一边”条件中的边是两角所夹的边,比如三角形的两个内角分别是60°和80°,它们所夹的边为2cm,你能画出这个三角形吗?你画的三角形与同伴画的一定全等吗?
2cm
80°
60°
【做一做】
测量、画三角形。同学们交流一下画这个三角形的步骤.
2cm
80°
60°
方法1:先画出BC=2 cm,然后画∠B=80°,最后画∠C=60°.
【做一做】
测量、画三角形。同学们交流一下画这个三角形的步骤.
2cm
80°
60°
方法2:先画出∠B=80°,然后画BC=2 cm,最后画∠C=60°.
改变角度和边长,你能得到同样的结论吗?
改变角度和边长,所画的三角形仍然全等。
同学把画出的三角形剪下来,与同小组比较,看是否重合.
画出的三角形都全等.
【总结归纳】
两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
在△ABC和△DEF中,
∠A=∠D,
AB=DE,
∠B=∠E ,
∴△ABC≌△DEF(ASA).
几何语言:
A
B
C
D
E
F
例1 如图,点D在AB上,点E在AC上,AB=AC, ∠B=∠C,试说明:△ACD≌△ABE.
A
B
C
D
E
解:在△ACD和△ABE中,
∠A=∠A(公共角 ),
AC=AB(已知),
∠C=∠B (已知 ),
∴ △ACD≌△ABE(ASA),
例2 已知:如图,点B,F,C,E在一条直线上,∠A=∠D,AC=DF,且AC∥DF.
试说明:△ABC≌△DEF.
解:∵AC∥DF,
∴∠ACB=∠DFE.
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA).
∠A=∠D(已知 ),
AC=DF(已知),
∠ACB=∠DFE (已证 ),
1.如图,AB∥FC,DE=EF,AB=15,CF=8,则BD等于( )。
A .8
B .7
C .6
D .5
A
B
C
D
E
F
B
随堂练习
2.如图,在△ABC中,AD⊥BC于D,BE⊥AC于E,BE与AD交于点F,AD=BD=5,则AF+CD的长度为( )
A. 10
B. 6
C. 5
D. 4.5
C
A
B
C
D
E
F
1
2
A
B
C
D
3.如图,在△ABC 中 ,∠B=∠C,AD是∠BAC的角平分线,那么AB=AC吗?为什么?
证明:∵ AD是∠BAC的角平分线
∴ AB=AC(全等三角形对应边相等)
∴ ∠ 1=∠2 (角平分线定义)
在△ABD与△ACD中
∴ △ABD≌△ACD(ASA)
∠1= ∠2 (已证)
∠B=∠C (已知)
AD=AD (公共边)
4.如图,AD∥BC,BE∥DF,AE=CF,试说明:△ADF≌△CBE.
解:∵AD∥BC,BE∥DF,
∴∠A=∠C,∠DFE=∠BEC.
∵AE=CF,∴AE+EF=CF+EF,
即AF=CE.
在ADF和△CBE中,
∵
∴△ADF≌△CBE(ASA).
∠A= ∠C
AF=CE
∠DFA= ∠BEC
本节课我们经历了对符合两角一边的条件的所有三角形进行画图验证,探索出三角形全等的另一种方法,它是:
两角和它们的夹边对应相等的两个三角形全等(ASA)
再加上前面学的(SSS),证明两个三角形全等共有两种方法,我们要学会根据题目给出的条件选用合适的定理来证明两个三角形全等。
角边角:两角及其夹边分别相等的两个三角形全等,简写成“角边角”或“ASA”.
在△ABC和△DEF中,
∠A=∠D,
AB=DE,
∠B=∠E ,
∴△ABC≌△DEF(ASA).
A
B
C
D
E
F
小结
三角形全等的判定
三角形全等的“ASA”判定:
两角及其夹边分别相等的两个三角形全等.
三角形全等的“AAS”判定:
两角分别相等且其中一组等角的对边相等的两个三角形全等.
注意两角与边位置关系的区别
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
