4.3 探索三角形全等的条件(第一课时)课件(共22张PPT)
文档属性
| 名称 | 4.3 探索三角形全等的条件(第一课时)课件(共22张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 6.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 00:00:00 | ||
图片预览






文档简介
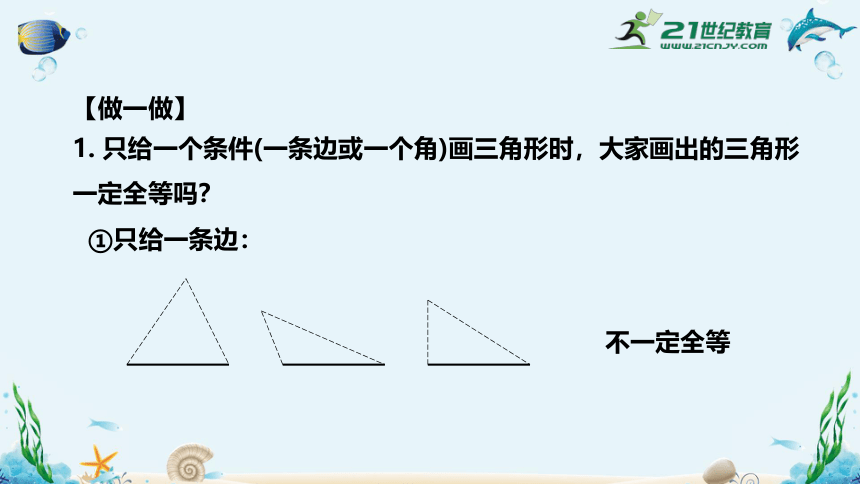
对应边相等,对应角相等.
1、 什么叫全等三角形?
能够完全重合的两个三角形叫 全等三角形.
2、 全等三角形有什么性质?
①AB=DE ② BC=EF ③ CA=FD
④ ∠A= ∠D ⑤ ∠B=∠E ⑥ ∠C= ∠F
A
B
C
D
E
F
满足几个条件的两个三角形全等呢?
3 第1课时
利用“SSS”判定三角形全等
【思考】
要画一个三角形与小明画的三角形全等,需要几个与边或角的大小有关的条件呢?一个条件?两个条件?三个条件?……
【做一做】
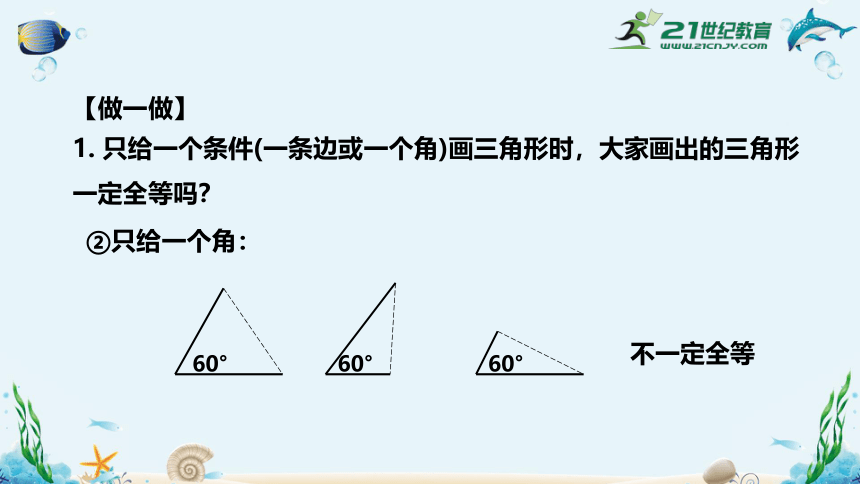
1. 只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?
①只给一条边:
不一定全等
②只给一个角:
60°
60°
60°
【做一做】
1. 只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?
不一定全等
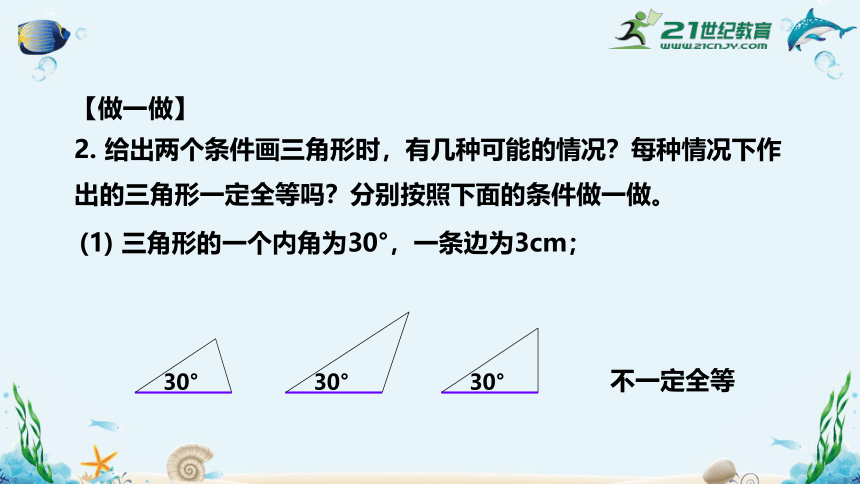
2. 给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做。
【做一做】
(1) 三角形的一个内角为30°,一条边为3cm;
30°
30°
30°
不一定全等
2. 给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做。
【做一做】
(2) 三角形的两个内角分别为30°和 50°;
30°
30°
50°
50°
不一定全等
2. 给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做。
【做一做】
(3) 三角形的两条边分别为4cm,6cm.
4cm
4cm
6cm
4cm
可以发现,只给出一个条件或两个条件时,都不能保证所画出的三角形一定全等。
如果给出三个条件画三角形,你能说出有哪几种可能的情况吗?
(1)三个角;
(2)三条边;
(3)两角一边;
(4)两边一角.
有四种可能:
(1) 已知一个三角形的三个内角分别为40°,60°和80°,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
【做一做】
三个内角对应相等的两个三角形不一定全等
40°
80°
60°
40°
80°
60°
(2) 已知一个三角形的三条边分别为4cm,5cm和7cm,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
【做一做】
5cm
4cm
7cm
A
B
C
(2) 已知一个三角形的三条边分别为4cm,5cm和7cm,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
【做一做】
三条边对应相等的两个三角形一定全等。
B'
C'
A'
作法:
(1)画B'C'=BC;
(2)分别以B'C'为圆心,线段AB,AC长为半径画圆,两弧相交于点A‘;
(3)连接线段A'B',A'C'
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。
【总结归纳】
A
B
C
D
E
F
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(SSS).
AB=DE,
BC=EF,
CA=FD,
用符号语言表达为:
例1 如图,有一个三角形钢架,AB =AC ,
AD 是连接点A 与BC 中点D 的支架.
说明:△ABD ≌△ACD .
解题思路:
先找隐含条件
公共边AD
再找现有条件
AB=AC
最后找准备条件
BD=CD
D是BC的中点
C
B
D
A
证明:∵ D 是BC中点,
∴ BD =DC.
在△ABD 与△ACD 中,
AB =AC (已知)
BD =CD (已证)
AD =AD (公共边)
∴ △ABD ≌ △ACD ( SSS ).
准备条件
指明范围
摆齐依据
写出结论
1.如图,E是AC上一点,AB=AD,BE=DE,可应用“SSS”证明三角形全等的是( )
A. △ABC≌△ADC
B. △ABE≌△ADE
C. △CBE≌△CDE
D. 以上选项都对
B
随堂练习
2.如图,△ABC中,AD=DE,AB=BE,∠A=100°,则∠DEC= 度.
80
3.如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.
证明:∠A=∠D.
证明:∵BE=CF,∴BE+EC=CF+EC,
即BC=EF.
在△ABC和△DEF中,
所以△ABC≌△DEF(SSS).所以∠A=∠D.
4.如图,在△ABC中,AC=BC,D是AB上的一点,AE⊥CD于点E,BF⊥CD于点F,若CE=BF,AE=EF+BF.
试判断AC与BC的位置关系,并说明理由.
解:AC⊥BC.
理由如下:因为CE=BF,AE=EF+BF,CF=CE+EF,所以AE=CF.
在△ACE和△CBF中,
所以△ACE≌△CBF(SSS).所以∠CAE=∠BCF.
因为∠CAE+∠ACE=90°,
所以∠ACE+∠BCF=90°.
所以∠ACB=90°.所以AC⊥BC.
这节课你学到了什么?
1. 三角形全等的条件:三边对应相等的两个三角形全等
(“边边边”或“SSS”)
2. 三角形具有稳定性。
本课小结
https://www.21cnjy.com/help/help_extract.php
1、 什么叫全等三角形?
能够完全重合的两个三角形叫 全等三角形.
2、 全等三角形有什么性质?
①AB=DE ② BC=EF ③ CA=FD
④ ∠A= ∠D ⑤ ∠B=∠E ⑥ ∠C= ∠F
A
B
C
D
E
F
满足几个条件的两个三角形全等呢?
3 第1课时
利用“SSS”判定三角形全等
【思考】
要画一个三角形与小明画的三角形全等,需要几个与边或角的大小有关的条件呢?一个条件?两个条件?三个条件?……
【做一做】
1. 只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?
①只给一条边:
不一定全等
②只给一个角:
60°
60°
60°
【做一做】
1. 只给一个条件(一条边或一个角)画三角形时,大家画出的三角形一定全等吗?
不一定全等
2. 给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做。
【做一做】
(1) 三角形的一个内角为30°,一条边为3cm;
30°
30°
30°
不一定全等
2. 给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做。
【做一做】
(2) 三角形的两个内角分别为30°和 50°;
30°
30°
50°
50°
不一定全等
2. 给出两个条件画三角形时,有几种可能的情况?每种情况下作出的三角形一定全等吗?分别按照下面的条件做一做。
【做一做】
(3) 三角形的两条边分别为4cm,6cm.
4cm
4cm
6cm
4cm
可以发现,只给出一个条件或两个条件时,都不能保证所画出的三角形一定全等。
如果给出三个条件画三角形,你能说出有哪几种可能的情况吗?
(1)三个角;
(2)三条边;
(3)两角一边;
(4)两边一角.
有四种可能:
(1) 已知一个三角形的三个内角分别为40°,60°和80°,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
【做一做】
三个内角对应相等的两个三角形不一定全等
40°
80°
60°
40°
80°
60°
(2) 已知一个三角形的三条边分别为4cm,5cm和7cm,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
【做一做】
5cm
4cm
7cm
A
B
C
(2) 已知一个三角形的三条边分别为4cm,5cm和7cm,你能画出这个三角形吗?把你画的三角形与同伴画出的进行比较,它们一定全等吗?
【做一做】
三条边对应相等的两个三角形一定全等。
B'
C'
A'
作法:
(1)画B'C'=BC;
(2)分别以B'C'为圆心,线段AB,AC长为半径画圆,两弧相交于点A‘;
(3)连接线段A'B',A'C'
三边对应相等的两个三角形全等,简写为“边边边”或“SSS”。
【总结归纳】
A
B
C
D
E
F
在△ABC和△ DEF中,
∴ △ABC ≌△ DEF(SSS).
AB=DE,
BC=EF,
CA=FD,
用符号语言表达为:
例1 如图,有一个三角形钢架,AB =AC ,
AD 是连接点A 与BC 中点D 的支架.
说明:△ABD ≌△ACD .
解题思路:
先找隐含条件
公共边AD
再找现有条件
AB=AC
最后找准备条件
BD=CD
D是BC的中点
C
B
D
A
证明:∵ D 是BC中点,
∴ BD =DC.
在△ABD 与△ACD 中,
AB =AC (已知)
BD =CD (已证)
AD =AD (公共边)
∴ △ABD ≌ △ACD ( SSS ).
准备条件
指明范围
摆齐依据
写出结论
1.如图,E是AC上一点,AB=AD,BE=DE,可应用“SSS”证明三角形全等的是( )
A. △ABC≌△ADC
B. △ABE≌△ADE
C. △CBE≌△CDE
D. 以上选项都对
B
随堂练习
2.如图,△ABC中,AD=DE,AB=BE,∠A=100°,则∠DEC= 度.
80
3.如图,点B,E,C,F在一条直线上,AB=DE,AC=DF,BE=CF.
证明:∠A=∠D.
证明:∵BE=CF,∴BE+EC=CF+EC,
即BC=EF.
在△ABC和△DEF中,
所以△ABC≌△DEF(SSS).所以∠A=∠D.
4.如图,在△ABC中,AC=BC,D是AB上的一点,AE⊥CD于点E,BF⊥CD于点F,若CE=BF,AE=EF+BF.
试判断AC与BC的位置关系,并说明理由.
解:AC⊥BC.
理由如下:因为CE=BF,AE=EF+BF,CF=CE+EF,所以AE=CF.
在△ACE和△CBF中,
所以△ACE≌△CBF(SSS).所以∠CAE=∠BCF.
因为∠CAE+∠ACE=90°,
所以∠ACE+∠BCF=90°.
所以∠ACB=90°.所以AC⊥BC.
这节课你学到了什么?
1. 三角形全等的条件:三边对应相等的两个三角形全等
(“边边边”或“SSS”)
2. 三角形具有稳定性。
本课小结
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
