4.1 认识三角形(第四课时)课件(共19张PPT)
文档属性
| 名称 | 4.1 认识三角形(第四课时)课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-12 21:16:19 | ||
图片预览




文档简介
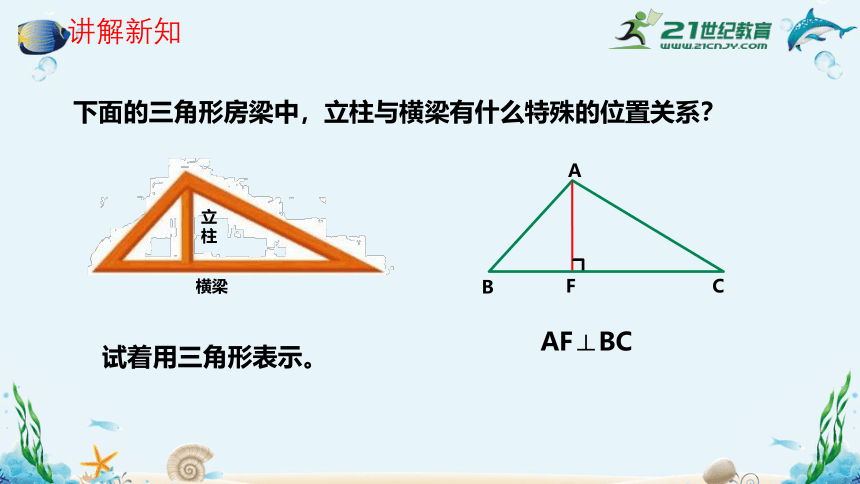
在三角形中,连接一个顶点与它对边中点的线段。
3.三角形的三条中线__________
2.填一填
∵BE是中线,∴_____=_____=
∵CF是中线,∴AB=2____=2____
AE
CE
AC
1
2
1.三角形的中线:
AF
BF
交于一点
导入新课
5.填一填
∵BE是△ABC的角平分线,∠ABE=______
∵CF是△ABC的角平分线,∴∠ACB=2______=2______
∠CBE
∠ACF
∠BCF
4.三角形的角平分线
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线。
第四章 三角形
1 认识三角形
第4课时 三角形的高
学 习 目 标
认识三角形的高,能画任意三角形的高,了解三角形三条
高所在直线交于一点;(重点)
学会用数学知识解决实际问题的能力,发展应用和自主探究
意识,培养学生的动手实践能力与合作精神.(重点)
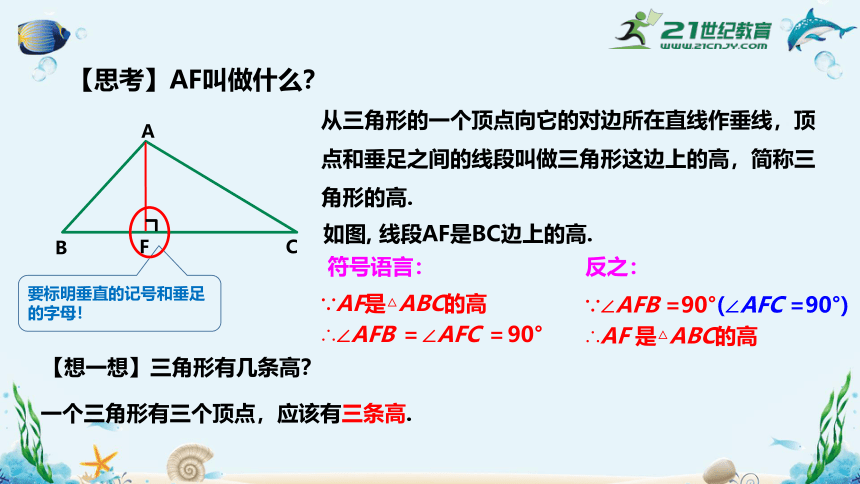
下面的三角形房梁中,立柱与横梁有什么特殊的位置关系?
立
柱
横梁
试着用三角形表示。
A
B
C
F
AF⊥BC
讲解新知
A
B
C
F
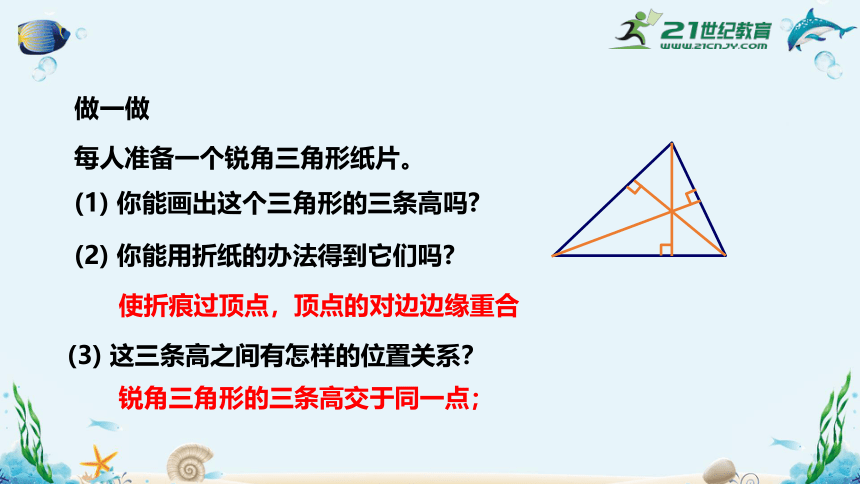
【思考】AF叫做什么?
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高,简称三角形的高.
如图, 线段AF是BC边上的高.
【想一想】三角形有几条高?
一个三角形有三个顶点,应该有三条高.
∵AF是△ABC的高
∴∠AFB =∠AFC =90°
符号语言:
反之:
∵∠AFB =90°(∠AFC =90°)
∴AF 是△ABC的高
要标明垂直的记号和垂足的字母!
做一做
每人准备一个锐角三角形纸片。
(1) 你能画出这个三角形的三条高吗?
(2) 你能用折纸的办法得到它们吗?
使折痕过顶点,顶点的对边边缘重合
(3) 这三条高之间有怎样的位置关系?
锐角三角形的三条高交于同一点;
议一议
在纸上画出一个直角三角形。
(1)画出直角三角形的三条高,
(2)它们有怎样的位置关系?
直角三角形的三条高交于直角顶点.
A
B
C
D
议一议
(1) 你能画出钝角三角形的三条高吗?
(2)钝角三角形的三条高交于一点吗?
钝角三角形的三条高不相交于一点。
(3)它们所在的直线交于一点吗?
钝角三角形的三条高所在直线交于一点。
A
B
C
D
F
O
E
{5940675A-B579-460E-94D1-54222C63F5DA}
【总结归纳】三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三条高所在直线的交点的位置
三角形内部
直角顶点
三角形外部
要点归纳
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 三角形
高及高的交点的位置
图示
锐角三角形
直角三角形
钝角三角形
三条高都在三角形的内部,三条高的交点在三角形的内部
直角三角形有两条高恰好是三角形的两条直角边,另一条高在三角形内部,三条高的交点是直角顶点
钝角三角形有两条高落在三角形的外部,另一条高在三角形内部,三条高没有交点,但三条高所在的直线交于三角形外一点
例1 作△ABC的边AB上的高,下列作法中,正确的是( )
规律总结:三角形任意一边上的高必须满足:(1)过该边所对的顶点;(2)垂足必须在该边或在该边的延长线上.
D
例2 如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
解:因为AD是△ABC的角平分线,∠BAC=60°,
所以∠DAC=∠BAD=30°.
因为CE是△ABC的高,∠BCE=40°,
所以∠B=50°,所以
∠ADB=180°-∠B-∠BAD
=180°-30°-50°
=100°.
例3 如图所示,在△???????????? 中,∠?????=?38°,∠?????=?54°, ???????? 是?????????边上的高,?????????是∠???????????? 的平分线. 求∠???????????? 的度数.
?
解:在△???????????? 中,∵ ∠?????=?38°,∠?????=?54°,
∴ ∠?????????????=?180°?? ∠??????∠?????= 180°??38°??54°=?88°?.
∵ ???????? 是∠?????????????的平分线,
∴ ∠???????????? = 12∠???????????? = 12 ×88°=?44°?.
∵ ???????? 是???????? 边上的高,∴ ∠?????????????=?90°?.
在△ ???????????? 中,∵ ∠???????????? = 90°,∠?????=?54°,
∴ ∠?????????????=?180°???∠??????????????∠?????=?180°??90°??54°=?36°?.
∴ ∠?????????????=∠????????????? ∠?????????????=?44°??36°=?8°?.
?
随堂训练
1.如图,在△ABC中,EF∥AC,BD⊥AC于点D,交
EF于点G,则下列说法错误的是( )
A.BD是△ABC的高 B.CD是△BCD的高
C.EG是△ABD的高 D.BG是△BEF的高
2.如图,CD、CE、CF分别是△ABC的高、角平分线、
中线,则下列各式中错误的是( )
A.AB=2BF B.∠ACE=∠ACB
C.AE=BE D.CD⊥BE
C
C
3.如图所示,在△ABC中,AB=AC=5,BC=6,
AD⊥BC于点D,且AD=4,若点P在边AC上移动,
则BP的最小值为____.
245
?
4.如图,在△ABC中,AB边上的高是____ ,BC边
上 的高是____ ;在△BCF中,CF边上的高是____ .
AD
BC
CE
5.在△????????????中,????????⊥????????于????,????????是∠????????????的平分线,∠????=20°,∠????=60°,求:
(1)∠????????????的度数;
(2)∠????????????的度数.
?
解:(1)∵????????⊥????????,∴∠????????????=90°.
∵∠????=60°,∴∠????????????=90°﹣∠????=90°﹣60°=30°;
(2)∵∠????=20°,∠????=60°,∠????+∠????+∠????????????=180°,
∴∠????????????=100°.
∵????????是∠????????????的平分线,∴∠????????????= 12∠????????????=50°,
∴∠????????????=∠????+∠????????????=20°+50°=70°,∠????????????=90°﹣70°=20°.
?
课堂小结
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 三角形
高及高的交点的位置
图示
锐角三角形
直角三角形
钝角三角形
三条高都在三角形的内部,三条高的交点在三角形的内部
直角三角形有两条高恰好是三角形的两条直角边,另一条高在三角形内部,三条高的交点是直角顶点
钝角三角形有两条高落在三角形的外部,另一条高在三角形内部,三条高没有交点,但三条高所在的直线交于三角形外一点
https://www.21cnjy.com/help/help_extract.php
3.三角形的三条中线__________
2.填一填
∵BE是中线,∴_____=_____=
∵CF是中线,∴AB=2____=2____
AE
CE
AC
1
2
1.三角形的中线:
AF
BF
交于一点
导入新课
5.填一填
∵BE是△ABC的角平分线,∠ABE=______
∵CF是△ABC的角平分线,∴∠ACB=2______=2______
∠CBE
∠ACF
∠BCF
4.三角形的角平分线
在三角形中,一个内角的平分线与它的对边相交,这个角的顶点与交点之间的线段,叫做三角形的角平分线。
第四章 三角形
1 认识三角形
第4课时 三角形的高
学 习 目 标
认识三角形的高,能画任意三角形的高,了解三角形三条
高所在直线交于一点;(重点)
学会用数学知识解决实际问题的能力,发展应用和自主探究
意识,培养学生的动手实践能力与合作精神.(重点)
下面的三角形房梁中,立柱与横梁有什么特殊的位置关系?
立
柱
横梁
试着用三角形表示。
A
B
C
F
AF⊥BC
讲解新知
A
B
C
F
【思考】AF叫做什么?
从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高,简称三角形的高.
如图, 线段AF是BC边上的高.
【想一想】三角形有几条高?
一个三角形有三个顶点,应该有三条高.
∵AF是△ABC的高
∴∠AFB =∠AFC =90°
符号语言:
反之:
∵∠AFB =90°(∠AFC =90°)
∴AF 是△ABC的高
要标明垂直的记号和垂足的字母!
做一做
每人准备一个锐角三角形纸片。
(1) 你能画出这个三角形的三条高吗?
(2) 你能用折纸的办法得到它们吗?
使折痕过顶点,顶点的对边边缘重合
(3) 这三条高之间有怎样的位置关系?
锐角三角形的三条高交于同一点;
议一议
在纸上画出一个直角三角形。
(1)画出直角三角形的三条高,
(2)它们有怎样的位置关系?
直角三角形的三条高交于直角顶点.
A
B
C
D
议一议
(1) 你能画出钝角三角形的三条高吗?
(2)钝角三角形的三条高交于一点吗?
钝角三角形的三条高不相交于一点。
(3)它们所在的直线交于一点吗?
钝角三角形的三条高所在直线交于一点。
A
B
C
D
F
O
E
{5940675A-B579-460E-94D1-54222C63F5DA}
【总结归纳】三角形的三条高的特性:
高所在的直线是否相交
高之间是否相交
高在三角形内部的数量
钝角三角形
直角三角形
锐角三角形
3
1
1
相交
相交
不相交
相交
相交
相交
三条高所在直线的交点的位置
三角形内部
直角顶点
三角形外部
要点归纳
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 三角形
高及高的交点的位置
图示
锐角三角形
直角三角形
钝角三角形
三条高都在三角形的内部,三条高的交点在三角形的内部
直角三角形有两条高恰好是三角形的两条直角边,另一条高在三角形内部,三条高的交点是直角顶点
钝角三角形有两条高落在三角形的外部,另一条高在三角形内部,三条高没有交点,但三条高所在的直线交于三角形外一点
例1 作△ABC的边AB上的高,下列作法中,正确的是( )
规律总结:三角形任意一边上的高必须满足:(1)过该边所对的顶点;(2)垂足必须在该边或在该边的延长线上.
D
例2 如图,已知AD是△ABC的角平分线,CE是△ABC的高,∠BAC=60°,∠BCE=40°,求∠ADB的度数.
解:因为AD是△ABC的角平分线,∠BAC=60°,
所以∠DAC=∠BAD=30°.
因为CE是△ABC的高,∠BCE=40°,
所以∠B=50°,所以
∠ADB=180°-∠B-∠BAD
=180°-30°-50°
=100°.
例3 如图所示,在△???????????? 中,∠?????=?38°,∠?????=?54°, ???????? 是?????????边上的高,?????????是∠???????????? 的平分线. 求∠???????????? 的度数.
?
解:在△???????????? 中,∵ ∠?????=?38°,∠?????=?54°,
∴ ∠?????????????=?180°?? ∠??????∠?????= 180°??38°??54°=?88°?.
∵ ???????? 是∠?????????????的平分线,
∴ ∠???????????? = 12∠???????????? = 12 ×88°=?44°?.
∵ ???????? 是???????? 边上的高,∴ ∠?????????????=?90°?.
在△ ???????????? 中,∵ ∠???????????? = 90°,∠?????=?54°,
∴ ∠?????????????=?180°???∠??????????????∠?????=?180°??90°??54°=?36°?.
∴ ∠?????????????=∠????????????? ∠?????????????=?44°??36°=?8°?.
?
随堂训练
1.如图,在△ABC中,EF∥AC,BD⊥AC于点D,交
EF于点G,则下列说法错误的是( )
A.BD是△ABC的高 B.CD是△BCD的高
C.EG是△ABD的高 D.BG是△BEF的高
2.如图,CD、CE、CF分别是△ABC的高、角平分线、
中线,则下列各式中错误的是( )
A.AB=2BF B.∠ACE=∠ACB
C.AE=BE D.CD⊥BE
C
C
3.如图所示,在△ABC中,AB=AC=5,BC=6,
AD⊥BC于点D,且AD=4,若点P在边AC上移动,
则BP的最小值为____.
245
?
4.如图,在△ABC中,AB边上的高是____ ,BC边
上 的高是____ ;在△BCF中,CF边上的高是____ .
AD
BC
CE
5.在△????????????中,????????⊥????????于????,????????是∠????????????的平分线,∠????=20°,∠????=60°,求:
(1)∠????????????的度数;
(2)∠????????????的度数.
?
解:(1)∵????????⊥????????,∴∠????????????=90°.
∵∠????=60°,∴∠????????????=90°﹣∠????=90°﹣60°=30°;
(2)∵∠????=20°,∠????=60°,∠????+∠????+∠????????????=180°,
∴∠????????????=100°.
∵????????是∠????????????的平分线,∴∠????????????= 12∠????????????=50°,
∴∠????????????=∠????+∠????????????=20°+50°=70°,∠????????????=90°﹣70°=20°.
?
课堂小结
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} 三角形
高及高的交点的位置
图示
锐角三角形
直角三角形
钝角三角形
三条高都在三角形的内部,三条高的交点在三角形的内部
直角三角形有两条高恰好是三角形的两条直角边,另一条高在三角形内部,三条高的交点是直角顶点
钝角三角形有两条高落在三角形的外部,另一条高在三角形内部,三条高没有交点,但三条高所在的直线交于三角形外一点
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
