六年级数学下册教案:5 数学广角——鸽巢问题(人教版)
文档属性
| 名称 | 六年级数学下册教案:5 数学广角——鸽巢问题(人教版) | 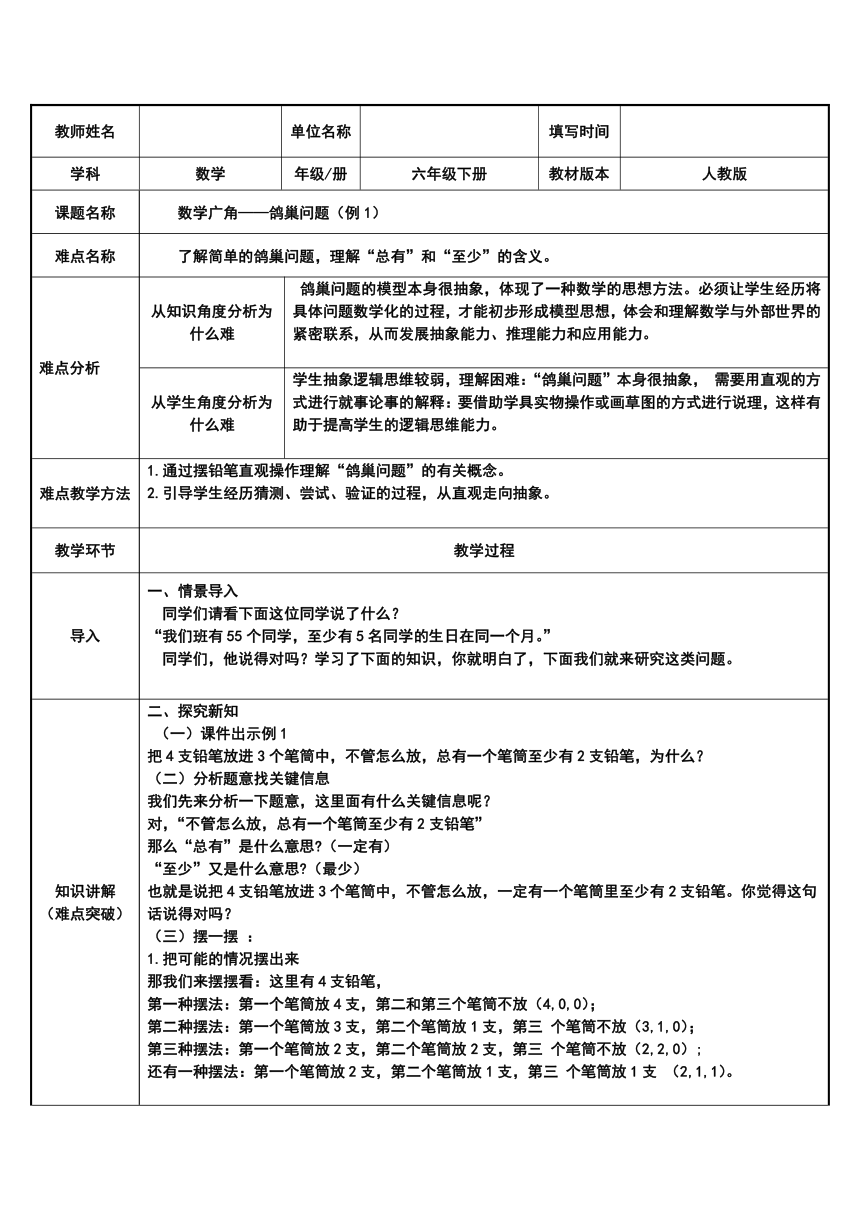 | |
| 格式 | docx | ||
| 文件大小 | 16.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-11 05:31:16 | ||
图片预览

文档简介
教师姓名
单位名称
填写时间
学科
数学
年级/册
六年级下册
教材版本
人教版
课题名称
数学广角——鸽巢问题(例1)
难点名称
了解简单的鸽巢问题,理解“总有”和“至少”的含义。
难点分析
从知识角度分析为什么难
鸽巢问题的模型本身很抽象,体现了一种数学的思想方法。必须让学生经历将具体问题数学化的过程,才能初步形成模型思想,体会和理解数学与外部世界的紧密联系,从而发展抽象能力、推理能力和应用能力。
从学生角度分析为什么难
学生抽象逻辑思维较弱,理解困难:“鸽巢问题”本身很抽象, 需要用直观的方式进行就事论事的解释:要借助学具实物操作或画草图的方式进行说理,这样有助于提高学生的逻辑思维能力。
难点教学方法
1.通过摆铅笔直观操作理解“鸽巢问题”的有关概念。
2.引导学生经历猜测、尝试、验证的过程,从直观走向抽象。
教学环节
教学过程
导入
一、情景导入
同学们请看下面这位同学说了什么?
“我们班有55个同学,至少有5名同学的生日在同一个月。”
同学们,他说得对吗?学习了下面的知识,你就明白了,下面我们就来研究这类问题。
知识讲解
(难点突破)
二、探究新知
(一)课件出示例1
把4支铅笔放进3个笔筒中,不管怎么放,总有一个笔筒至少有2支铅笔,为什么?
(二)分析题意找关键信息
我们先来分析一下题意,这里面有什么关键信息呢?
对,“不管怎么放,总有一个笔筒至少有2支铅笔”
那么“总有”是什么意思?(一定有)
“至少”又是什么意思?(最少)
也就是说把4支铅笔放进3个笔筒中,不管怎么放,一定有一个笔筒里至少有2支铅笔。你觉得这句话说得对吗?
(三)摆一摆 :
1.把可能的情况摆出来
那我们来摆摆看:这里有4支铅笔,
第一种摆法:第一个笔筒放4支,第二和第三个笔筒不放(4,0,0);
第二种摆法:第一个笔筒放3支,第二个笔筒放1支,第三 个笔筒不放(3,1,0);
第三种摆法:第一个笔筒放2支,第二个笔筒放2支,第三 个笔筒不放(2,2,0);
还有一种摆法:第一个笔筒放2支,第二个笔筒放1支,第三 个笔筒放1支 (2,1,1)。
2.枚举法的定义
像这样把所以可能的情况都列举出来的方法叫做枚举法。
3.观察验证
凭什么说总有一个笔筒里至少有2支铅笔呢?我们来看看刚才的摆法。(观察刚才的4种摆法,把符合要求的笔筒标出来予以“检验”,理解“总有一个笔筒里至少有2支铅笔”)
4.假设法
其实我们还可以用更直接方法,只摆一种情况就能得到这个结论,也就是用假设法: 先将3支铅笔,在每个笔筒中放1支,剩下的1支就要放进其中的一个笔筒。这时无论放到哪个笔筒,那个笔筒中就有两支了。所以至少有一个笔筒中有2支铅笔。
(四)总结发现:
现在我们就会发现,无论怎样摆,总有一个笔筒里至少有2支铅笔。像这类问题我们就叫做“鸽巢问题”。
4支铅笔————4只鸽子
3个笔筒———3个鸽巢
把4个要分的物体放进3个鸽巢里,不管怎么放,至少有一个鸽巢有2个物体。同学们明白了吗?
课堂练习
(难点巩固)
练习再验证
1.出示做一做
教师:刚才我们通过不同的方法验证了这句话是正确,现在我们来看到做一做:
5只鸽子飞进了3个鸽笼,总有一个鸽笼至少飞进了多少只鸽子?为什么?
对,是2鸽子。
2.动画演示验证
我们先来看动画演示,先是三只鸽子各飞进一个笼子,剩下的两只也分别各飞进一个笼子。
5只鸽子相当于物体, 3个鸽笼就是鸽巢,当物体的个数大于鸽巢的个数,不论怎么飞,总有一个鸽巢至少飞进两只鸽子。
小结
三、归纳总结
(一)“鸽巢原理(一)”定义
这就是“鸽巢原理(一)” :把n+1个物体任意放进n个鸽巢中,(n是非0自然数),那么一定有一个鸽巢中至少放进了2个物体。
(二)拓展升华
同学们都懂了吗?那前面那位同学说的生日问题你理解了吗?好,我们今天的课就上到这里,再见。
单位名称
填写时间
学科
数学
年级/册
六年级下册
教材版本
人教版
课题名称
数学广角——鸽巢问题(例1)
难点名称
了解简单的鸽巢问题,理解“总有”和“至少”的含义。
难点分析
从知识角度分析为什么难
鸽巢问题的模型本身很抽象,体现了一种数学的思想方法。必须让学生经历将具体问题数学化的过程,才能初步形成模型思想,体会和理解数学与外部世界的紧密联系,从而发展抽象能力、推理能力和应用能力。
从学生角度分析为什么难
学生抽象逻辑思维较弱,理解困难:“鸽巢问题”本身很抽象, 需要用直观的方式进行就事论事的解释:要借助学具实物操作或画草图的方式进行说理,这样有助于提高学生的逻辑思维能力。
难点教学方法
1.通过摆铅笔直观操作理解“鸽巢问题”的有关概念。
2.引导学生经历猜测、尝试、验证的过程,从直观走向抽象。
教学环节
教学过程
导入
一、情景导入
同学们请看下面这位同学说了什么?
“我们班有55个同学,至少有5名同学的生日在同一个月。”
同学们,他说得对吗?学习了下面的知识,你就明白了,下面我们就来研究这类问题。
知识讲解
(难点突破)
二、探究新知
(一)课件出示例1
把4支铅笔放进3个笔筒中,不管怎么放,总有一个笔筒至少有2支铅笔,为什么?
(二)分析题意找关键信息
我们先来分析一下题意,这里面有什么关键信息呢?
对,“不管怎么放,总有一个笔筒至少有2支铅笔”
那么“总有”是什么意思?(一定有)
“至少”又是什么意思?(最少)
也就是说把4支铅笔放进3个笔筒中,不管怎么放,一定有一个笔筒里至少有2支铅笔。你觉得这句话说得对吗?
(三)摆一摆 :
1.把可能的情况摆出来
那我们来摆摆看:这里有4支铅笔,
第一种摆法:第一个笔筒放4支,第二和第三个笔筒不放(4,0,0);
第二种摆法:第一个笔筒放3支,第二个笔筒放1支,第三 个笔筒不放(3,1,0);
第三种摆法:第一个笔筒放2支,第二个笔筒放2支,第三 个笔筒不放(2,2,0);
还有一种摆法:第一个笔筒放2支,第二个笔筒放1支,第三 个笔筒放1支 (2,1,1)。
2.枚举法的定义
像这样把所以可能的情况都列举出来的方法叫做枚举法。
3.观察验证
凭什么说总有一个笔筒里至少有2支铅笔呢?我们来看看刚才的摆法。(观察刚才的4种摆法,把符合要求的笔筒标出来予以“检验”,理解“总有一个笔筒里至少有2支铅笔”)
4.假设法
其实我们还可以用更直接方法,只摆一种情况就能得到这个结论,也就是用假设法: 先将3支铅笔,在每个笔筒中放1支,剩下的1支就要放进其中的一个笔筒。这时无论放到哪个笔筒,那个笔筒中就有两支了。所以至少有一个笔筒中有2支铅笔。
(四)总结发现:
现在我们就会发现,无论怎样摆,总有一个笔筒里至少有2支铅笔。像这类问题我们就叫做“鸽巢问题”。
4支铅笔————4只鸽子
3个笔筒———3个鸽巢
把4个要分的物体放进3个鸽巢里,不管怎么放,至少有一个鸽巢有2个物体。同学们明白了吗?
课堂练习
(难点巩固)
练习再验证
1.出示做一做
教师:刚才我们通过不同的方法验证了这句话是正确,现在我们来看到做一做:
5只鸽子飞进了3个鸽笼,总有一个鸽笼至少飞进了多少只鸽子?为什么?
对,是2鸽子。
2.动画演示验证
我们先来看动画演示,先是三只鸽子各飞进一个笼子,剩下的两只也分别各飞进一个笼子。
5只鸽子相当于物体, 3个鸽笼就是鸽巢,当物体的个数大于鸽巢的个数,不论怎么飞,总有一个鸽巢至少飞进两只鸽子。
小结
三、归纳总结
(一)“鸽巢原理(一)”定义
这就是“鸽巢原理(一)” :把n+1个物体任意放进n个鸽巢中,(n是非0自然数),那么一定有一个鸽巢中至少放进了2个物体。
(二)拓展升华
同学们都懂了吗?那前面那位同学说的生日问题你理解了吗?好,我们今天的课就上到这里,再见。
