北师大版七下 2.3 《平行线的性质》课件(24张)
文档属性
| 名称 | 北师大版七下 2.3 《平行线的性质》课件(24张) |  | |
| 格式 | pptx | ||
| 文件大小 | 489.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 17:58:44 | ||
图片预览






文档简介
3
第二章平行线与相交线
平行线的性质
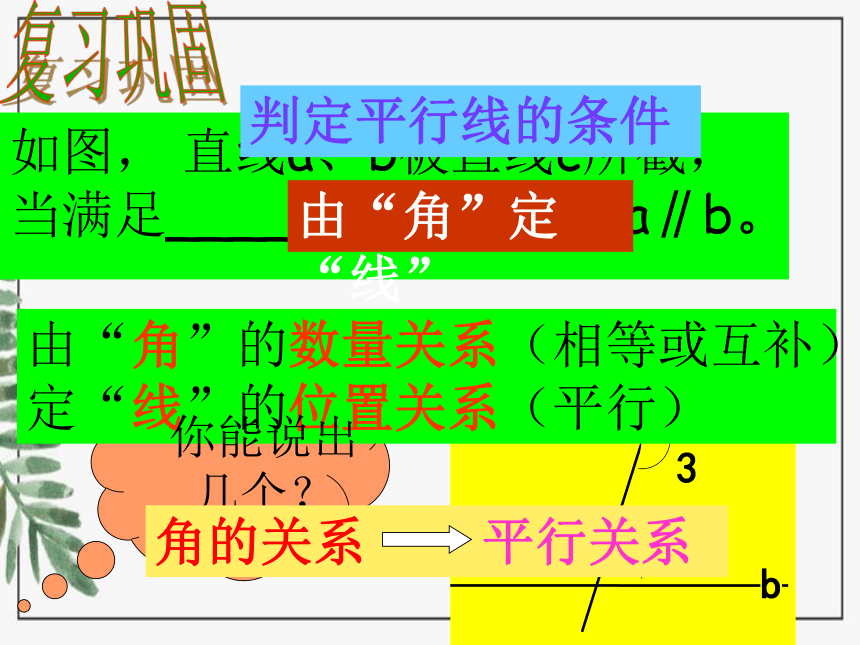
复习巩固
如图, 直线a、b被直线c所截,当满足_______条件时, a∥b。
a
b
c
1
3
2
4
判定平行线的条件
由“角”定“线”
由“角”的数量关系(相等或互补)定“线”的位置关系(平行)
你能说出 几个?
角的关系 平行关系
如图,直线a与直线b平行
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
a
b
c
(1)测量同位角∠1与∠5,它们有什么关系?还有其它的同位角吗?它们的大小关系如何?
(2)图中有几对内错角?它们的大小有什么关系?为什么?
(3)图中有几对同旁内角?它们的大小有什么关系?为什么?
相等
2对,互补
2对,相等
由此你能想到了什么?
结论 ?
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
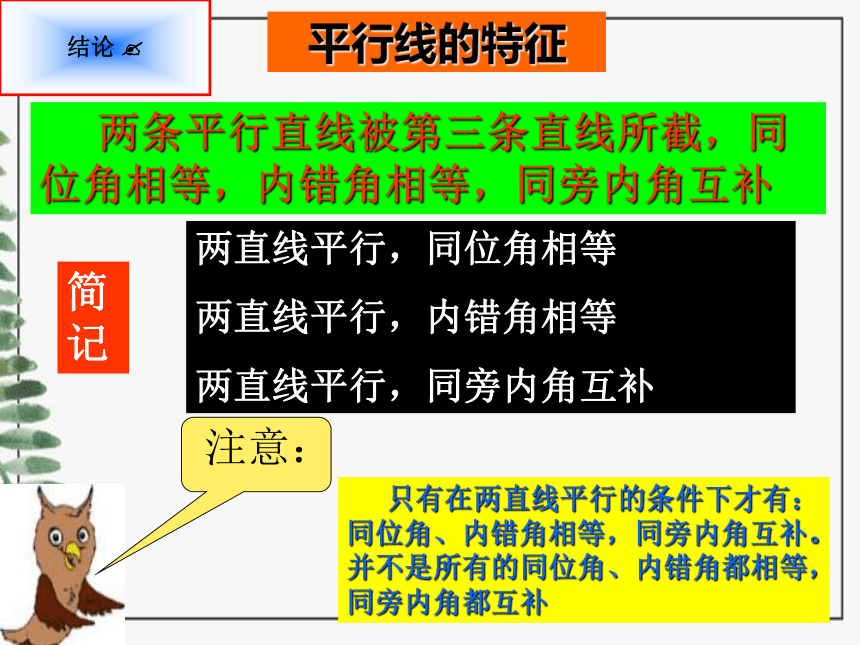
平行线的特征
两条平行直线被第三条直线所截,同位角相等,内错角相等,同旁内角互补
简记
注意:
只有在两直线平行的条件下才有:同位角、内错角相等,同旁内角互补。并不是所有的同位角、内错角都相等,同旁内角都互补
练一练
如图,已知直线a, b被直线c所截,在括号内为下面各小题的推理填上适当的根据:
(1)∵a∥b,∴ ∠1=∠3 ( )
(3)∵a∥b,∴ ∠1=∠2 ( )
(2)∵∠1=∠3,∴ a∥b ( )
(5)∵∠1=∠2 ,∴ a∥b ( )
(4)∵a∥b,∴ ∠1+∠4=180°( )
(6)∵∠1+∠4=180°,∴ a∥b ( )
两直线平行,同位角相等
同位角相等,两直线平行
两直线平行,内错角相等
两直线平行,同旁内角互补
内错角相等,两直线平行
同旁内角互补,两直线平行
1
2
a
b
c
3
4
两条平行直线被第三条直线所截,同位角相等,内错角相等,同旁内角互补。
两直线平行,同位角相等。
简记为:
两直线平行,内错角相等。
两直线平行,同旁内角互补。
1
2
a
b
c
3
4
如右图:(1)a∥b(已知)
→ ∠1=∠2 ( )
两直线平行,同位角相等
(2)a∥b(已知)
→∠2=∠3 ( )
两直线平行,内错角相等
(3)a∥b(已知)
→∠2+∠4 =180°( )
两直线平行,同旁内角互补
5
6
7
8
E
D
C
A
B
1
2
3
2、如图:已知BD是∠ABC的平分线,∠2=∠3
∵BD是∠ABC的平分线( )
∴∠____ = ∠____(角平分线定义)
又∵∠2=∠3( )
∴∠1=∠3( )
∴AB____DE( )
∴∠CDE=∠______( )
已知
1
2
等量代换
∥
已知
内错角相等,两直线平行
两直线平行,同位角相等
A
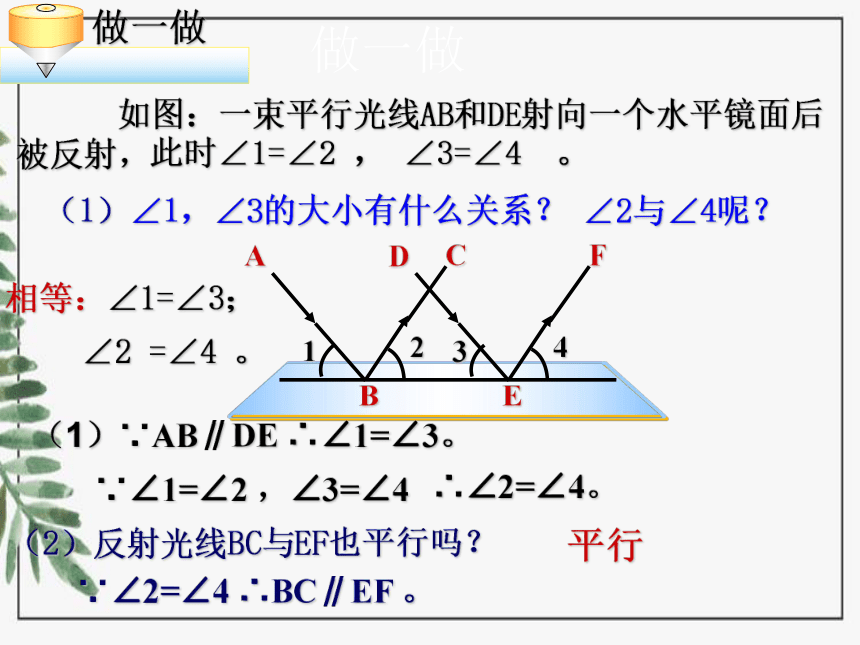
做一做
做一做
如图:一束平行光线AB和DE射向一个水平镜面后被反射,
(1)∠1,∠3的大小有什么关系?
∠2与∠4呢?
(1)∵AB∥DE ∴∠1=∠3。
相等:∠1=∠3;
(2)反射光线BC与EF也平行吗?
∵∠2=∠4 ∴BC∥EF 。
平行
∵∠1=∠2 ,∠3=∠4
∴∠2=∠4。
A
B
D
E
C
F
此时∠1=∠2 , ∠3=∠4 。
1
3
2
4
∠2 =∠4 。
考古
位于中国四川省广汉市南兴镇北的三星堆遗址,属于古蜀国文明。遗址分布范围达12平方公里,距今4800年至2800年,延续时间近2000年。
出土了各种文物:金器、玉器、石器、陶器、青铜器...等数千件。其中有享誉中外的金杖、金面罩、青铜人像、头像、人立像、画具等精品文物1000多件。
三星堆遗址
考古发现的问题
A
B
C
D
115°
110°
如图,是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=110°。已知梯形的两底AD//BC,请你求出另外两个角的度数。
解: ∵AD//BC ,∠A=115°
∴∠A+∠B=180 °(两直线平 行,同旁内角互补)
∴∠B=180°- ∠A=65°
比一比 、乐一乐:(分组比赛)
规则:(组长上来抽签、读题,组内讨论后派
一人回答,并说明理由)
苹果
香蕉
草莓
桔子
梨子
西瓜
桃子
杨梅
苹果
香蕉
草莓
桔子
苹果题:
梨子
西瓜
桃子
杨梅
如图,要在一座房子的两侧铺设平行管道,如果房子一侧铺设的角度为120,那么,为了使管道对接,另一侧应以什么角度铺设?为什么?
120o
°
香蕉题:
苹果
香蕉
草莓
桔子
梨子
西瓜
桃子
杨梅
如图:AB,CD被EF所截,AB∥CD(填空)。
若∠1=120o,则∠2= __ ( )
∠3= -∠1=___
( )
A
B
C
D
E
F
1
2
3
180o
草莓题:
苹果
香蕉
草莓
桔子
梨子
西瓜
桃子
杨梅
1、如果AD//BC,根据___________
可得∠B=∠1
2、如果AB//CD,根据___________
可得∠D=∠1
3、如果AD//BC,根据___________
可得∠C+_______=180?
A
B
C
D
1
桔子题:
苹果
香蕉
草莓
桔子
梨子
西瓜
桃子
杨梅
如图:在墙面上安装一管道需经两次拐弯,拐弯后的管道与拐弯前的管道平行。若第一个弯道处∠B=142o,那么第二个弯道处∠C为多少度?为什么?
A
B
C
梨子题:
苹果
香蕉
草莓
桔子
梨子
西瓜
桃子
杨梅
本题免答
谢谢
祝你好运
西瓜题:
苹果
香蕉
草莓
桔子
梨子
西瓜
桃子
杨梅
如图,a∥b,c、d是截线,∠1=80 ,∠5=70 .
∠2、∠3、∠4各是多少度?为什么?
°
°
2
a
b
c
d
1
3
5
4
桃子题:
苹果
香蕉
草莓
桔子
梨子
西瓜
桃子
杨梅
如图,平行线AB、CD被直线AE所截.
(1)从∠1=110 可以知道∠2
是多少度?为什么?
(2)从∠1=110 可以知道∠3
是多少度?为什么?
(3)从∠1=110 可以知道∠4
是多少度?为什么?
2
1
D
C
B
A
E
4
3
°
°
°
杨梅题:
苹果
香蕉
草莓
桔子
梨子
西瓜
桃子
杨梅
已知:直线a∥b, ∠1=115°.
则: ∠2=___,理由:________.
若∠3= 115°,则:直线c与d有何位置关系?并说明理由.
a
b
c
d
1
3
2
3、已知:如图,直线 a∥b,c∥d,1=110°
求 :∠2,∠3的度数.
解(1)∵ c∥d(已知)
∴∠1=∠4( )
又∵ ∠3=∠4( )
∴∠1=∠3(等量代换)
∵∠1=110°(已知)
∴ ∠3= (等量代换)
(2)∵a∥b(已知)
∴∠2+∠4=180°( )
∴∠2= .
两直线平行,同位角相等
对顶角相等
110°
两直线平行,同旁内角互补
180°- 110°= 70°
学后小结
由“线”定“角”
由“线”的位置关系(平行),定“角”的数量关系(相等或互补)
平行线的特征
平行关系 角的关系
本课小结
平行线的特征
直线平行的条件
两直线平行,同位角相等。
两直线平行,内错角相等。
两直线平行,同旁内角互补。
同位角相等,两直线平行。
内错角相等,两直线平行。
同旁内角互补,两直线平行。
潜能
激发
拓广探究:两条平行直线被第三条直线所截,一对同位角的角平分线有何位置关系?内错角的角平分线、同旁内角的角平分线它们分别又有何位置关系呢?
聪明的伙伴相信通过你们的认真观察、操作、推理、交流等活动,一定能发现其中的奥秘。试试看…
再 见
第二章平行线与相交线
平行线的性质
复习巩固
如图, 直线a、b被直线c所截,当满足_______条件时, a∥b。
a
b
c
1
3
2
4
判定平行线的条件
由“角”定“线”
由“角”的数量关系(相等或互补)定“线”的位置关系(平行)
你能说出 几个?
角的关系 平行关系
如图,直线a与直线b平行
1
2
3
4
5
6
7
8
1
2
3
4
5
6
7
8
a
b
c
(1)测量同位角∠1与∠5,它们有什么关系?还有其它的同位角吗?它们的大小关系如何?
(2)图中有几对内错角?它们的大小有什么关系?为什么?
(3)图中有几对同旁内角?它们的大小有什么关系?为什么?
相等
2对,互补
2对,相等
由此你能想到了什么?
结论 ?
两直线平行,同位角相等
两直线平行,内错角相等
两直线平行,同旁内角互补
平行线的特征
两条平行直线被第三条直线所截,同位角相等,内错角相等,同旁内角互补
简记
注意:
只有在两直线平行的条件下才有:同位角、内错角相等,同旁内角互补。并不是所有的同位角、内错角都相等,同旁内角都互补
练一练
如图,已知直线a, b被直线c所截,在括号内为下面各小题的推理填上适当的根据:
(1)∵a∥b,∴ ∠1=∠3 ( )
(3)∵a∥b,∴ ∠1=∠2 ( )
(2)∵∠1=∠3,∴ a∥b ( )
(5)∵∠1=∠2 ,∴ a∥b ( )
(4)∵a∥b,∴ ∠1+∠4=180°( )
(6)∵∠1+∠4=180°,∴ a∥b ( )
两直线平行,同位角相等
同位角相等,两直线平行
两直线平行,内错角相等
两直线平行,同旁内角互补
内错角相等,两直线平行
同旁内角互补,两直线平行
1
2
a
b
c
3
4
两条平行直线被第三条直线所截,同位角相等,内错角相等,同旁内角互补。
两直线平行,同位角相等。
简记为:
两直线平行,内错角相等。
两直线平行,同旁内角互补。
1
2
a
b
c
3
4
如右图:(1)a∥b(已知)
→ ∠1=∠2 ( )
两直线平行,同位角相等
(2)a∥b(已知)
→∠2=∠3 ( )
两直线平行,内错角相等
(3)a∥b(已知)
→∠2+∠4 =180°( )
两直线平行,同旁内角互补
5
6
7
8
E
D
C
A
B
1
2
3
2、如图:已知BD是∠ABC的平分线,∠2=∠3
∵BD是∠ABC的平分线( )
∴∠____ = ∠____(角平分线定义)
又∵∠2=∠3( )
∴∠1=∠3( )
∴AB____DE( )
∴∠CDE=∠______( )
已知
1
2
等量代换
∥
已知
内错角相等,两直线平行
两直线平行,同位角相等
A
做一做
做一做
如图:一束平行光线AB和DE射向一个水平镜面后被反射,
(1)∠1,∠3的大小有什么关系?
∠2与∠4呢?
(1)∵AB∥DE ∴∠1=∠3。
相等:∠1=∠3;
(2)反射光线BC与EF也平行吗?
∵∠2=∠4 ∴BC∥EF 。
平行
∵∠1=∠2 ,∠3=∠4
∴∠2=∠4。
A
B
D
E
C
F
此时∠1=∠2 , ∠3=∠4 。
1
3
2
4
∠2 =∠4 。
考古
位于中国四川省广汉市南兴镇北的三星堆遗址,属于古蜀国文明。遗址分布范围达12平方公里,距今4800年至2800年,延续时间近2000年。
出土了各种文物:金器、玉器、石器、陶器、青铜器...等数千件。其中有享誉中外的金杖、金面罩、青铜人像、头像、人立像、画具等精品文物1000多件。
三星堆遗址
考古发现的问题
A
B
C
D
115°
110°
如图,是举世闻名的三星堆考古中发掘出的一个梯形残缺玉片,工作人员从玉片上已经量得∠A=115°,∠D=110°。已知梯形的两底AD//BC,请你求出另外两个角的度数。
解: ∵AD//BC ,∠A=115°
∴∠A+∠B=180 °(两直线平 行,同旁内角互补)
∴∠B=180°- ∠A=65°
比一比 、乐一乐:(分组比赛)
规则:(组长上来抽签、读题,组内讨论后派
一人回答,并说明理由)
苹果
香蕉
草莓
桔子
梨子
西瓜
桃子
杨梅
苹果
香蕉
草莓
桔子
苹果题:
梨子
西瓜
桃子
杨梅
如图,要在一座房子的两侧铺设平行管道,如果房子一侧铺设的角度为120,那么,为了使管道对接,另一侧应以什么角度铺设?为什么?
120o
°
香蕉题:
苹果
香蕉
草莓
桔子
梨子
西瓜
桃子
杨梅
如图:AB,CD被EF所截,AB∥CD(填空)。
若∠1=120o,则∠2= __ ( )
∠3= -∠1=___
( )
A
B
C
D
E
F
1
2
3
180o
草莓题:
苹果
香蕉
草莓
桔子
梨子
西瓜
桃子
杨梅
1、如果AD//BC,根据___________
可得∠B=∠1
2、如果AB//CD,根据___________
可得∠D=∠1
3、如果AD//BC,根据___________
可得∠C+_______=180?
A
B
C
D
1
桔子题:
苹果
香蕉
草莓
桔子
梨子
西瓜
桃子
杨梅
如图:在墙面上安装一管道需经两次拐弯,拐弯后的管道与拐弯前的管道平行。若第一个弯道处∠B=142o,那么第二个弯道处∠C为多少度?为什么?
A
B
C
梨子题:
苹果
香蕉
草莓
桔子
梨子
西瓜
桃子
杨梅
本题免答
谢谢
祝你好运
西瓜题:
苹果
香蕉
草莓
桔子
梨子
西瓜
桃子
杨梅
如图,a∥b,c、d是截线,∠1=80 ,∠5=70 .
∠2、∠3、∠4各是多少度?为什么?
°
°
2
a
b
c
d
1
3
5
4
桃子题:
苹果
香蕉
草莓
桔子
梨子
西瓜
桃子
杨梅
如图,平行线AB、CD被直线AE所截.
(1)从∠1=110 可以知道∠2
是多少度?为什么?
(2)从∠1=110 可以知道∠3
是多少度?为什么?
(3)从∠1=110 可以知道∠4
是多少度?为什么?
2
1
D
C
B
A
E
4
3
°
°
°
杨梅题:
苹果
香蕉
草莓
桔子
梨子
西瓜
桃子
杨梅
已知:直线a∥b, ∠1=115°.
则: ∠2=___,理由:________.
若∠3= 115°,则:直线c与d有何位置关系?并说明理由.
a
b
c
d
1
3
2
3、已知:如图,直线 a∥b,c∥d,1=110°
求 :∠2,∠3的度数.
解(1)∵ c∥d(已知)
∴∠1=∠4( )
又∵ ∠3=∠4( )
∴∠1=∠3(等量代换)
∵∠1=110°(已知)
∴ ∠3= (等量代换)
(2)∵a∥b(已知)
∴∠2+∠4=180°( )
∴∠2= .
两直线平行,同位角相等
对顶角相等
110°
两直线平行,同旁内角互补
180°- 110°= 70°
学后小结
由“线”定“角”
由“线”的位置关系(平行),定“角”的数量关系(相等或互补)
平行线的特征
平行关系 角的关系
本课小结
平行线的特征
直线平行的条件
两直线平行,同位角相等。
两直线平行,内错角相等。
两直线平行,同旁内角互补。
同位角相等,两直线平行。
内错角相等,两直线平行。
同旁内角互补,两直线平行。
潜能
激发
拓广探究:两条平行直线被第三条直线所截,一对同位角的角平分线有何位置关系?内错角的角平分线、同旁内角的角平分线它们分别又有何位置关系呢?
聪明的伙伴相信通过你们的认真观察、操作、推理、交流等活动,一定能发现其中的奥秘。试试看…
再 见
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
