北师大版七下:3.1 用表格表示的变量间关系 课件(20张)
文档属性
| 名称 | 北师大版七下:3.1 用表格表示的变量间关系 课件(20张) |  | |
| 格式 | pptx | ||
| 文件大小 | 496.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 17:58:44 | ||
图片预览







文档简介
七年级下册
3.1 用表格表示的变量间关系
通过阅读教材,完成下列填空
在一个变化过程中数值保持不变的量叫做______,可以取不同数值的量叫做______,如果一个量随着另外一个量的变化而变化,那么把这个量叫做__________,另一个量叫做__________.
教材助读
常量
变量
因变量
自变量
学习目标
经历探索具体情境中两个变量之间关系的过程,获得探索变量之间关系的体验,进一步发展符号感.
在具体情境中理解什么是变量、自变量、因变量,并能举出反映变量之间关系的例子.
1
2
能从表格中获得变量之间关系的信息,能用表格表示变量之间的关系,并根据表格中的资料尝试对变化趋势进行初步的预测.
3
情境导入
春
夏
秋
冬
情境导入
多年前的小男孩
如今的巨星
细心体会哦!
20
0
40
60
80
100
单位:cm
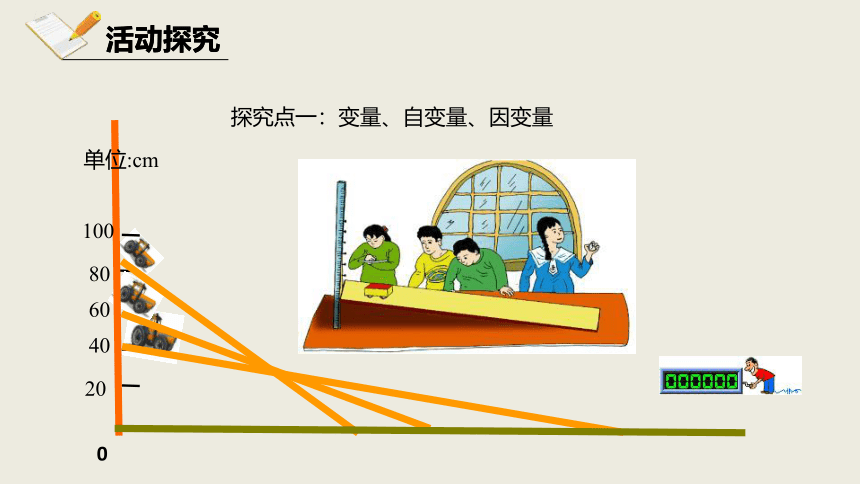
活动探究
活动探究
探究点一:变量、自变量、因变量
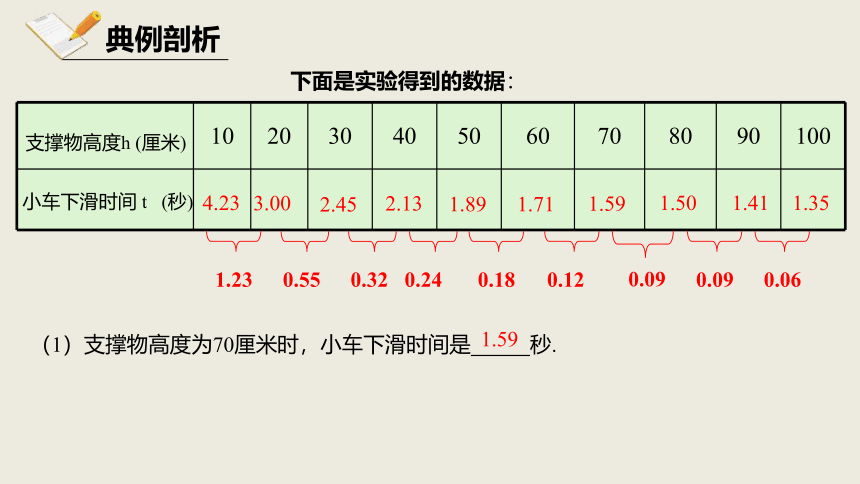
典例剖析
下面是实验得到的数据:
10
20
30
40
50
60
70
80
90
100
4.23
1.35
1.41
1.50
1.59
1.71
1.89
2.13
2.45
3.00
支撑物高度h (厘米)
小车下滑时间 t (秒)
1.23
0.55
0.32
0.24
0.18
0.12
0.09
0.09
0.06
(1)支撑物高度为70厘米时,小车下滑时间是 秒.
1.59
典例剖析
下面是实验得到的数据:
(2)如果用h(厘米)表示支撑物高度,t(秒)表示小车下滑时间,随着h逐渐变大,t的变化趋势是什么?
随着h逐渐变大,t逐渐变小.
10
20
30
40
50
60
70
80
90
100
4.23
1.35
1.41
1.50
1.59
1.71
1.89
2.13
2.45
3.00
支撑物高度h (厘米)
小车下滑时间 t (秒)
1.23
0.55
0.32
0.24
0.18
0.12
0.09
0.09
0.06
典例剖析
(3)h每增加10厘米,t的变化情况吗?
t的变化越来越小
下面是实验得到的数据:
10
20
30
40
50
60
70
80
90
100
4.23
1.35
1.41
1.50
1.59
1.71
1.89
2.13
2.45
3.00
支撑物高度h (厘米)
小车下滑时间 t (秒)
1.23
0.55
0.32
0.24
0.18
0.12
0.09
0.09
0.06
典例剖析
(4)估计当h=110厘米时,t的值是多少?你是怎样估计的?
1.35秒到1.29秒中的任一值
下面是实验得到的数据:
10
20
30
40
50
60
70
80
90
100
4.23
1.35
1.41
1.50
1.59
1.71
1.89
2.13
2.45
3.00
支撑物高度h (厘米)
小车下滑时间 t (秒)
1.23
0.55
0.32
0.24
0.18
0.12
0.09
0.09
0.06
在《小车下滑的时间》 中:
支撑物的高度h和小车下滑的时间t都在变化,它们都是变量(variable).
支撑物的高度h是自变量 (independent variable).
小车下滑的时间t是因变量 (dependent variable).
借助表格可以表示因变量随自变量变化而变化的情况.
其中小车下滑的时间t随支撑物的高度h的变化而变化.
小车下滑的距离(木板长度)一直没有变化.在变化过程中始终不变的量叫常量
举一反三
时间(秒)
0
1
2
3
4
5
6
7
8
9
10
速度(米/秒)
0
0.3
1.3
2.8
4.9
7.6
11.0
14.1
18.4
24.2
28.9
一辆小汽车在高速公路上从静止到启动10秒后的速度经测量如下表:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用t表示时间,v表示速度,那么随着t的变化,v的变化趋势是什么?
(3)当t 每增加1秒时,v的变化情况相同吗?在哪1秒钟内,v的增加最大?
(4)若高速公路上小汽车行驶速度的上限为120千米/时,试估计大约还需几秒这辆小汽车速度就将达到这个上限?
举一反三
我国从1949年到1999年的人口统计数据如下(精确到0.01亿):
时间/年x
1949
1959
1969
1979
1989
1999
人口/亿y
5.42
6.72
8.07
9.75
11.07
12.59
(1)x和y中, 是自变量, 是因变量.
(2)如果用x表示时间,y表示我国人口总数,那么随着x的变化,y的变化趋势是 .
随着x的增加,y也增加
x
y
你能观察表格,准确描述变量之间的变化趋势了吗?
变 量
1.自变量是在一定范围内主动变化的量.
2.因变量是随自变量变化而变化的量.
自变量
因变量
主动变化的量
被动变化的量
总结
在变化过程中,若有两个变量x和y, 其中y随着x 的变化而发生变化,我们就把x叫自变量,y叫因变量.
3.表格可以表示因变量随自变量变化而变化的情况,还能帮助我们对变化趋势进行初步的预测.
随堂检测
x
0
1
2
3
4
5
y
10
10.5
11
11.5
12
12.5
1、骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,在这一问题中,因变量是( ).
A、沙漠 B、体温 C、时间 D、骆驼
2、弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下面的关系:
下列说法不正确的是( )
A、x与y都是变量,x是自变量,y是因变量
B、弹簧不挂重物时的长度为0cm
C、物体质量每增加1kg,弹簧长度y增加0.5cm
D、所挂物体质量为7kg时,弹簧长度为13.5cm
B
B
随堂检测
时间/小时
0
4
8
12
16
20
24
水位/米
2
2.5
3
4
5
6
8
3、烧一壶水,十分钟后水开了.在这一过程中, 是变量,
是自变量, 是因变量.
4、某河受暴雨袭击,某天此河水的水位记录为下表:
(1)表中反映了 和 之间的关系,自变量是 ,因变量是 .
(2)12小时,水位是 ,
(3)水位上升最快的时间段是 .
时间和水温
时间
水温
时间 水位
时间
水位
4m
20--24
课堂小结
本节课都学到了什么?
变 量
自变量
因变量
主动变化的量
被动变化的量
个性化作业
日期
星期一
星期二
星期三
星期四
星期五
星期六
星期日
桶中剩水
4.5加仑
3.9加仑
3.5加仑
3.1加仑
2.5加仑
2加仑
1.5加仑
1.三口之家,冬天饮用桶装矿泉水的情况如下表:
(1)根据表中的数据,说一说哪些量是在发生变化?自变量和因变量各是什么?
(2)能说出下周一桶中还有多少水吗?
(3)根据表格中的数据,说一说星期一到星期日,桶中的水是如何变化的.
个性化作业
月份
1
2
3
4
5
6
7
8
9
10
11
12
价格
5.00
5.50
5.00
4.80
2.00
1.50
1.00
0.90
1.50
2.00
3.00
3.50
2.某种蔬菜的价格随季节变化如下表:
单位:元/千克
(1)观察表说出变量、自变量、因变量;
(2)哪个月这种蔬菜价格最高,哪个月这种蔬菜的价格最低;
(3)计算一下这种蔬菜的年平均价.
再见
3.1 用表格表示的变量间关系
通过阅读教材,完成下列填空
在一个变化过程中数值保持不变的量叫做______,可以取不同数值的量叫做______,如果一个量随着另外一个量的变化而变化,那么把这个量叫做__________,另一个量叫做__________.
教材助读
常量
变量
因变量
自变量
学习目标
经历探索具体情境中两个变量之间关系的过程,获得探索变量之间关系的体验,进一步发展符号感.
在具体情境中理解什么是变量、自变量、因变量,并能举出反映变量之间关系的例子.
1
2
能从表格中获得变量之间关系的信息,能用表格表示变量之间的关系,并根据表格中的资料尝试对变化趋势进行初步的预测.
3
情境导入
春
夏
秋
冬
情境导入
多年前的小男孩
如今的巨星
细心体会哦!
20
0
40
60
80
100
单位:cm
活动探究
活动探究
探究点一:变量、自变量、因变量
典例剖析
下面是实验得到的数据:
10
20
30
40
50
60
70
80
90
100
4.23
1.35
1.41
1.50
1.59
1.71
1.89
2.13
2.45
3.00
支撑物高度h (厘米)
小车下滑时间 t (秒)
1.23
0.55
0.32
0.24
0.18
0.12
0.09
0.09
0.06
(1)支撑物高度为70厘米时,小车下滑时间是 秒.
1.59
典例剖析
下面是实验得到的数据:
(2)如果用h(厘米)表示支撑物高度,t(秒)表示小车下滑时间,随着h逐渐变大,t的变化趋势是什么?
随着h逐渐变大,t逐渐变小.
10
20
30
40
50
60
70
80
90
100
4.23
1.35
1.41
1.50
1.59
1.71
1.89
2.13
2.45
3.00
支撑物高度h (厘米)
小车下滑时间 t (秒)
1.23
0.55
0.32
0.24
0.18
0.12
0.09
0.09
0.06
典例剖析
(3)h每增加10厘米,t的变化情况吗?
t的变化越来越小
下面是实验得到的数据:
10
20
30
40
50
60
70
80
90
100
4.23
1.35
1.41
1.50
1.59
1.71
1.89
2.13
2.45
3.00
支撑物高度h (厘米)
小车下滑时间 t (秒)
1.23
0.55
0.32
0.24
0.18
0.12
0.09
0.09
0.06
典例剖析
(4)估计当h=110厘米时,t的值是多少?你是怎样估计的?
1.35秒到1.29秒中的任一值
下面是实验得到的数据:
10
20
30
40
50
60
70
80
90
100
4.23
1.35
1.41
1.50
1.59
1.71
1.89
2.13
2.45
3.00
支撑物高度h (厘米)
小车下滑时间 t (秒)
1.23
0.55
0.32
0.24
0.18
0.12
0.09
0.09
0.06
在《小车下滑的时间》 中:
支撑物的高度h和小车下滑的时间t都在变化,它们都是变量(variable).
支撑物的高度h是自变量 (independent variable).
小车下滑的时间t是因变量 (dependent variable).
借助表格可以表示因变量随自变量变化而变化的情况.
其中小车下滑的时间t随支撑物的高度h的变化而变化.
小车下滑的距离(木板长度)一直没有变化.在变化过程中始终不变的量叫常量
举一反三
时间(秒)
0
1
2
3
4
5
6
7
8
9
10
速度(米/秒)
0
0.3
1.3
2.8
4.9
7.6
11.0
14.1
18.4
24.2
28.9
一辆小汽车在高速公路上从静止到启动10秒后的速度经测量如下表:
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果用t表示时间,v表示速度,那么随着t的变化,v的变化趋势是什么?
(3)当t 每增加1秒时,v的变化情况相同吗?在哪1秒钟内,v的增加最大?
(4)若高速公路上小汽车行驶速度的上限为120千米/时,试估计大约还需几秒这辆小汽车速度就将达到这个上限?
举一反三
我国从1949年到1999年的人口统计数据如下(精确到0.01亿):
时间/年x
1949
1959
1969
1979
1989
1999
人口/亿y
5.42
6.72
8.07
9.75
11.07
12.59
(1)x和y中, 是自变量, 是因变量.
(2)如果用x表示时间,y表示我国人口总数,那么随着x的变化,y的变化趋势是 .
随着x的增加,y也增加
x
y
你能观察表格,准确描述变量之间的变化趋势了吗?
变 量
1.自变量是在一定范围内主动变化的量.
2.因变量是随自变量变化而变化的量.
自变量
因变量
主动变化的量
被动变化的量
总结
在变化过程中,若有两个变量x和y, 其中y随着x 的变化而发生变化,我们就把x叫自变量,y叫因变量.
3.表格可以表示因变量随自变量变化而变化的情况,还能帮助我们对变化趋势进行初步的预测.
随堂检测
x
0
1
2
3
4
5
y
10
10.5
11
11.5
12
12.5
1、骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,在这一问题中,因变量是( ).
A、沙漠 B、体温 C、时间 D、骆驼
2、弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂的物体的重量x(kg)间有下面的关系:
下列说法不正确的是( )
A、x与y都是变量,x是自变量,y是因变量
B、弹簧不挂重物时的长度为0cm
C、物体质量每增加1kg,弹簧长度y增加0.5cm
D、所挂物体质量为7kg时,弹簧长度为13.5cm
B
B
随堂检测
时间/小时
0
4
8
12
16
20
24
水位/米
2
2.5
3
4
5
6
8
3、烧一壶水,十分钟后水开了.在这一过程中, 是变量,
是自变量, 是因变量.
4、某河受暴雨袭击,某天此河水的水位记录为下表:
(1)表中反映了 和 之间的关系,自变量是 ,因变量是 .
(2)12小时,水位是 ,
(3)水位上升最快的时间段是 .
时间和水温
时间
水温
时间 水位
时间
水位
4m
20--24
课堂小结
本节课都学到了什么?
变 量
自变量
因变量
主动变化的量
被动变化的量
个性化作业
日期
星期一
星期二
星期三
星期四
星期五
星期六
星期日
桶中剩水
4.5加仑
3.9加仑
3.5加仑
3.1加仑
2.5加仑
2加仑
1.5加仑
1.三口之家,冬天饮用桶装矿泉水的情况如下表:
(1)根据表中的数据,说一说哪些量是在发生变化?自变量和因变量各是什么?
(2)能说出下周一桶中还有多少水吗?
(3)根据表格中的数据,说一说星期一到星期日,桶中的水是如何变化的.
个性化作业
月份
1
2
3
4
5
6
7
8
9
10
11
12
价格
5.00
5.50
5.00
4.80
2.00
1.50
1.00
0.90
1.50
2.00
3.00
3.50
2.某种蔬菜的价格随季节变化如下表:
单位:元/千克
(1)观察表说出变量、自变量、因变量;
(2)哪个月这种蔬菜价格最高,哪个月这种蔬菜的价格最低;
(3)计算一下这种蔬菜的年平均价.
再见
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
