北师大版七下:3.2 用关系式表示的变量间关系 课件(20张)
文档属性
| 名称 | 北师大版七下:3.2 用关系式表示的变量间关系 课件(20张) |

|
|
| 格式 | pptx | ||
| 文件大小 | 540.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-05-10 00:00:00 | ||
图片预览





文档简介
用关系式表示的变量间关系
小车下滑的时间t是 ________
在“小车下滑的时间”实验中:
支撑物的高度h和小车下滑的时间t 都在变化,它们都是变量。
其中小车下滑的时间t
随支撑物的高度h的变化
而变化,
支撑物的高度h是________
被动发生变
化的量
主动发生变
化的量
回顾与思考
自变量
因变量
在这一变化过程中,小车下滑的
距离(木板的长度)一直没有变化.
像这种在变化过程中数值始终不变
的量叫做常量.
始终不变
的量
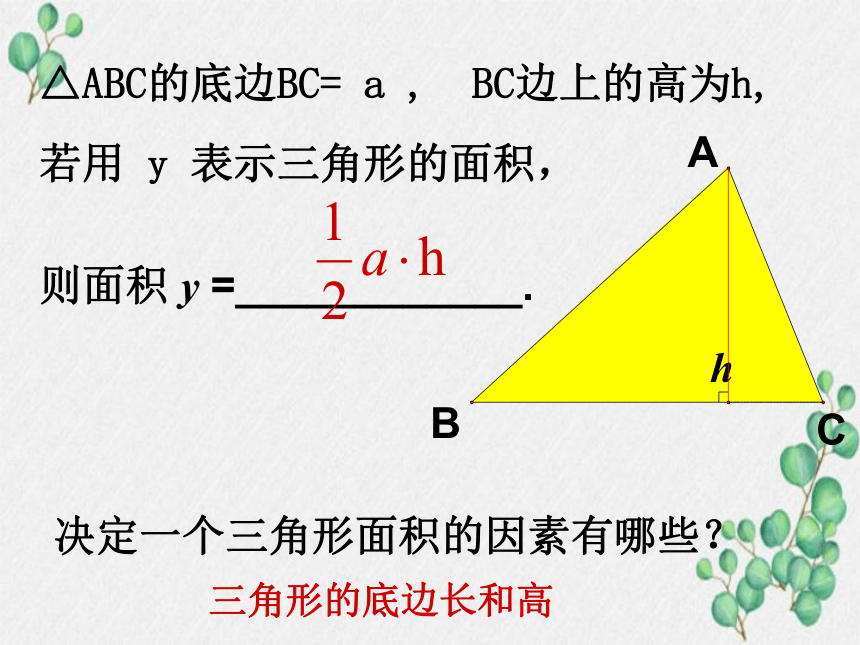
则面积 y =____________.
△ABC的底边BC= a , BC边上的高为h,
若用 y 表示三角形的面积,
h
B
C
A
决定一个三角形面积的因素有哪些?
三角形的底边长和高
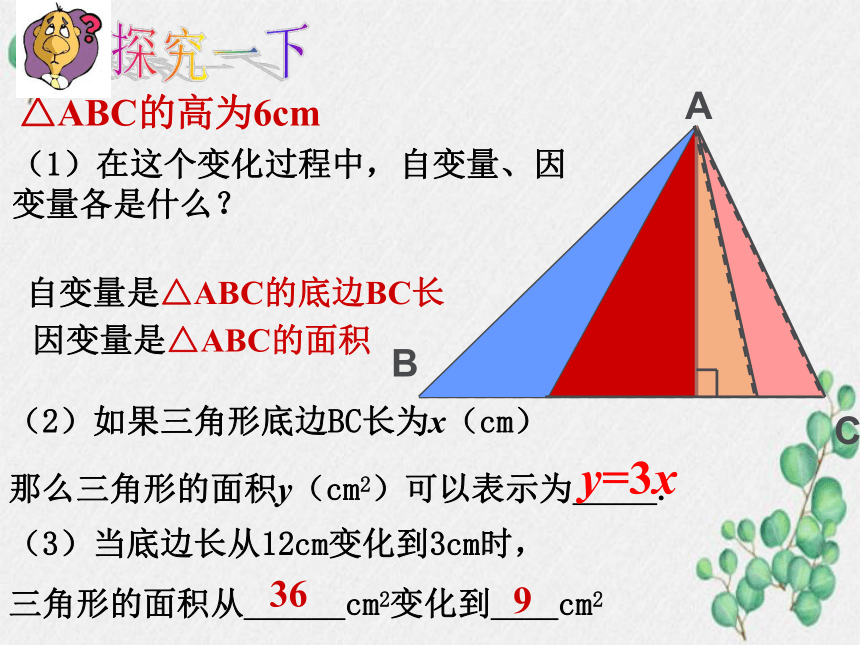
(1)在这个变化过程中,自变量、因变量各是什么?
(2)如果三角形底边BC长为x(cm)
那么三角形的面积y(cm2)可以表示为 .
A
B
C
y=3x
自变量是△ABC的底边BC长
因变量是△ABC的面积
△ABC的高为6cm
探究一下
(3)当底边长从12cm变化到3cm时,
三角形的面积从______cm2变化到____cm2
36
9
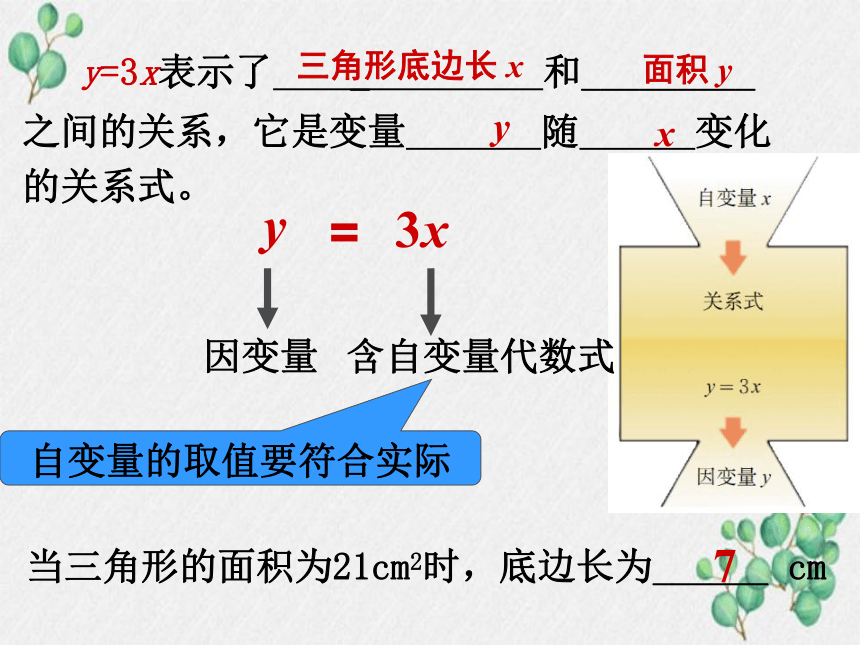
y=3x表示了 _ 和_________ 之间的关系,它是变量 随 变化的关系式。
三角形底边长 x
面积 y
3x
含自变量代数式
因变量
y
x
=
y
当三角形的面积为21cm2时,底边长为______ cm
7
自变量的取值要符合实际
自学检测一
1.将一个长为20cm,宽为10cm的长方形的四个角,
分别剪去大小相等的正方形,若被剪去正方形
的边长为 x cm , 阴影部分的面积为 y(cm2) ,
则 y 与 x 的关系式是 .
y=200 - 4x2
你还记得圆锥的体积公式是什么吗?
其中的字母表示什么?
复习回顾
r 表示圆锥的底面半径
h 表示圆锥的高
V 表示圆锥的体积
(2)如果圆锥底面半径为r(cm),
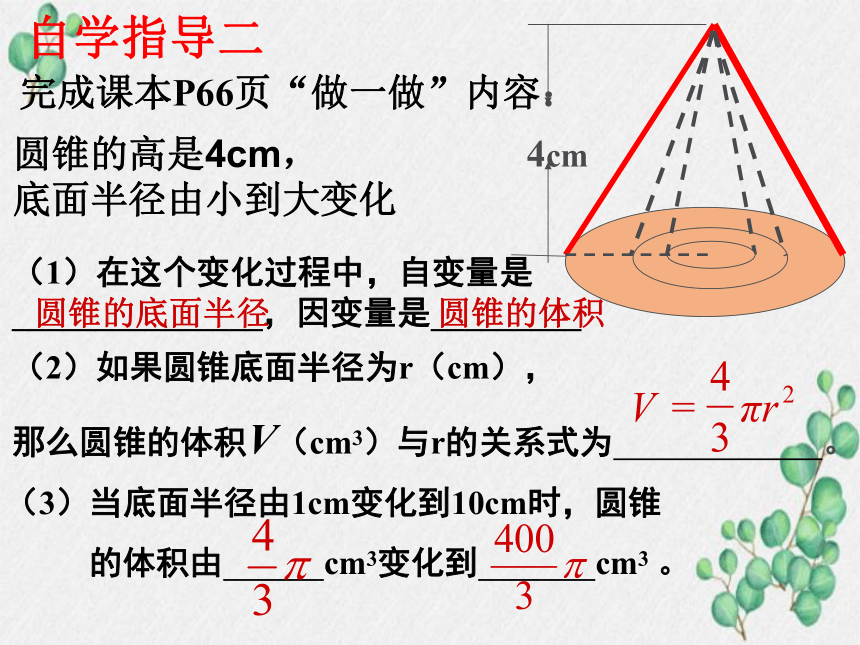
那么圆锥的体积V(cm3)与r的关系式为 。
(3)当底面半径由1cm变化到10cm时,圆锥
的体积由 cm3变化到 cm3 。
(1)在这个变化过程中,自变量是_______________,因变量是_________
4cm
完成课本P66页“做一做”内容:
圆锥的底面半径
圆锥的体积
圆锥的高是4cm,
底面半径由小到大变化
自学指导二
(1)在这个变化过程中,自变量是
__________ ,
因变量是 .
(2)如果圆锥的高为h cm,那么圆锥的体积V 与 h 之
间的关系式为 。
(3)当高 h 由1 cm变化到10 cm时,圆锥的体积由
_______cm3变化到 ________cm3。
变式
圆锥的底面半径2cm,高由小到大变化
圆锥的高
圆锥的体积
(1)家居用电的二氧化碳排放量可以用关系式表示为_____________,
其中的字母表示:
y = 0.785x
y 为家居用电的二氧化碳排放量 ;
x 为耗电量 。
议一议(P67)
(2)在上述关系式中,耗电量每增加
1 KW·h,二氧化碳排放量增加___________。当耗电量
从1 KW·h增加到100
KW·h时,二氧化碳排
放量从_______增加
到_________。
0.785kg
0.785kg
78.5kg
(3)小明家本月用电大约110 KW·h、天然气20m3、自来水5t、油耗75L,请你计算一下小明家这几项的二氧化碳排放量。
1、在地球某地,温度T(℃)与高度d
(m)的关系可以近似地用
来表示,根据这个关系式,当
d的值分别是200,400,600,
800,1000时,计算相应的T值,
并用表格表示所得结果。
随堂练习(P67)
高度
d/m
0
200
400
600
800
1000
温度
T/ ℃
10.00
8.67
7.33
6.00
4.67
3.33
某弹簧的自然长度为3cm,在弹性限度内所挂的物体的重量 x 每增加1 kg,弹簧长度 y 增加0.5cm。
x/kg
1
2
3
4
5
……
y/cm
……
依据上表数据,写出y与x之间的关系式。
3.5
y = 3+0.5x
4
4.5
5
5.5
巩固训练
1.根据表格列出关系式
1kg
2kg
3kg
3.5cm
4cm
4.5cm
3cm
2、某轿车油箱中原来有油40千克,现在知道
行驶时间t(时)与剩下油量Q(千克)的关系如下表:
行驶时间t/时
剩下油量Q/千克
1
40-6
2
40-12
3
40-18
4
40-24
5
40-30
…
…
请写出用t表示Q的关系式。
并思考轿车能行驶7小时吗?
3.有一边长为 3 cm的正方形,若边长增加时,
则其面积也随之变化。
(1)若边长增加了x cm,则其面积 y(cm2)
关于x的关系式是_______________
(2)当 x 由 3cm 变化到 7cm 时,
其面积 y 由________cm2变化到_________cm2
y=(3+x )2
36
100
解:
4.某市出租车计费标准如下:行驶路程不超过
3千米时,收费8元;行驶路程超过3千米的
部分,按每千米1.60元计费。
(1)求出租车收费y(元)与行驶路程x(千米)
之间的关系式;
(2)若某人一次乘出租车时,付了车费14.40元,
求他这次乘车坐了多少千米的路程?
(1)当x≤3时,y=8;
(2)当y=14.40时,1.6x+3.2=14.40,解得x=7
故他这次乘车坐了7千米的路程。
当x>3时,y=8+1.6(x-3)
=1.6x+3.2
课本P68页
习题3.2
第1,3题
作业
小车下滑的时间t是 ________
在“小车下滑的时间”实验中:
支撑物的高度h和小车下滑的时间t 都在变化,它们都是变量。
其中小车下滑的时间t
随支撑物的高度h的变化
而变化,
支撑物的高度h是________
被动发生变
化的量
主动发生变
化的量
回顾与思考
自变量
因变量
在这一变化过程中,小车下滑的
距离(木板的长度)一直没有变化.
像这种在变化过程中数值始终不变
的量叫做常量.
始终不变
的量
则面积 y =____________.
△ABC的底边BC= a , BC边上的高为h,
若用 y 表示三角形的面积,
h
B
C
A
决定一个三角形面积的因素有哪些?
三角形的底边长和高
(1)在这个变化过程中,自变量、因变量各是什么?
(2)如果三角形底边BC长为x(cm)
那么三角形的面积y(cm2)可以表示为 .
A
B
C
y=3x
自变量是△ABC的底边BC长
因变量是△ABC的面积
△ABC的高为6cm
探究一下
(3)当底边长从12cm变化到3cm时,
三角形的面积从______cm2变化到____cm2
36
9
y=3x表示了 _ 和_________ 之间的关系,它是变量 随 变化的关系式。
三角形底边长 x
面积 y
3x
含自变量代数式
因变量
y
x
=
y
当三角形的面积为21cm2时,底边长为______ cm
7
自变量的取值要符合实际
自学检测一
1.将一个长为20cm,宽为10cm的长方形的四个角,
分别剪去大小相等的正方形,若被剪去正方形
的边长为 x cm , 阴影部分的面积为 y(cm2) ,
则 y 与 x 的关系式是 .
y=200 - 4x2
你还记得圆锥的体积公式是什么吗?
其中的字母表示什么?
复习回顾
r 表示圆锥的底面半径
h 表示圆锥的高
V 表示圆锥的体积
(2)如果圆锥底面半径为r(cm),
那么圆锥的体积V(cm3)与r的关系式为 。
(3)当底面半径由1cm变化到10cm时,圆锥
的体积由 cm3变化到 cm3 。
(1)在这个变化过程中,自变量是_______________,因变量是_________
4cm
完成课本P66页“做一做”内容:
圆锥的底面半径
圆锥的体积
圆锥的高是4cm,
底面半径由小到大变化
自学指导二
(1)在这个变化过程中,自变量是
__________ ,
因变量是 .
(2)如果圆锥的高为h cm,那么圆锥的体积V 与 h 之
间的关系式为 。
(3)当高 h 由1 cm变化到10 cm时,圆锥的体积由
_______cm3变化到 ________cm3。
变式
圆锥的底面半径2cm,高由小到大变化
圆锥的高
圆锥的体积
(1)家居用电的二氧化碳排放量可以用关系式表示为_____________,
其中的字母表示:
y = 0.785x
y 为家居用电的二氧化碳排放量 ;
x 为耗电量 。
议一议(P67)
(2)在上述关系式中,耗电量每增加
1 KW·h,二氧化碳排放量增加___________。当耗电量
从1 KW·h增加到100
KW·h时,二氧化碳排
放量从_______增加
到_________。
0.785kg
0.785kg
78.5kg
(3)小明家本月用电大约110 KW·h、天然气20m3、自来水5t、油耗75L,请你计算一下小明家这几项的二氧化碳排放量。
1、在地球某地,温度T(℃)与高度d
(m)的关系可以近似地用
来表示,根据这个关系式,当
d的值分别是200,400,600,
800,1000时,计算相应的T值,
并用表格表示所得结果。
随堂练习(P67)
高度
d/m
0
200
400
600
800
1000
温度
T/ ℃
10.00
8.67
7.33
6.00
4.67
3.33
某弹簧的自然长度为3cm,在弹性限度内所挂的物体的重量 x 每增加1 kg,弹簧长度 y 增加0.5cm。
x/kg
1
2
3
4
5
……
y/cm
……
依据上表数据,写出y与x之间的关系式。
3.5
y = 3+0.5x
4
4.5
5
5.5
巩固训练
1.根据表格列出关系式
1kg
2kg
3kg
3.5cm
4cm
4.5cm
3cm
2、某轿车油箱中原来有油40千克,现在知道
行驶时间t(时)与剩下油量Q(千克)的关系如下表:
行驶时间t/时
剩下油量Q/千克
1
40-6
2
40-12
3
40-18
4
40-24
5
40-30
…
…
请写出用t表示Q的关系式。
并思考轿车能行驶7小时吗?
3.有一边长为 3 cm的正方形,若边长增加时,
则其面积也随之变化。
(1)若边长增加了x cm,则其面积 y(cm2)
关于x的关系式是_______________
(2)当 x 由 3cm 变化到 7cm 时,
其面积 y 由________cm2变化到_________cm2
y=(3+x )2
36
100
解:
4.某市出租车计费标准如下:行驶路程不超过
3千米时,收费8元;行驶路程超过3千米的
部分,按每千米1.60元计费。
(1)求出租车收费y(元)与行驶路程x(千米)
之间的关系式;
(2)若某人一次乘出租车时,付了车费14.40元,
求他这次乘车坐了多少千米的路程?
(1)当x≤3时,y=8;
(2)当y=14.40时,1.6x+3.2=14.40,解得x=7
故他这次乘车坐了7千米的路程。
当x>3时,y=8+1.6(x-3)
=1.6x+3.2
课本P68页
习题3.2
第1,3题
作业
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
